《动手学深度学习 Pytorch版》 6.1 从全连接层到卷积
6.1.1 不变性
-
平移不变性(translation invariance):
不管检测对象出现在图像中的哪个位置,神经网络的前面几层应该对相同的图像区域具有相似的反应,即为“平移不变性”。
-
局部性(locality):
神经网络的前面几层应该只探索输入图像中的局部区域,而不过度在意图像中相隔较远区域的关系,这就是“局部性”原则。最终,可以聚合这些局部特征,以在整个图像级别进行预测。
6.1.2 多层感知机的限制
假设多层感知机的输入是 X X X,将其隐藏表示记为 H H H(二者形状相同)。
使用 [ X ] i j [\boldsymbol{X}]_{ij} [X]ij 和 [ H ] i j [\boldsymbol{H}]_{ij} [H]ij 表示位置 ( i , j ) (i,j) (i,j) 位置上的像素点。
因为每个像素点都需要和其他像素点联系,故每个像素点都需要一个二阶的权重张量,又由于是二维图像,故最终权重张量 W \mathrm{W} W 为四维。
再假设偏置参数为 U U U,则可以将全连接层表示为:
[ H ] i j = [ U ] i j + ∑ k ∑ l [ W ] i , j , k , l [ X ] k , l [\boldsymbol{H}]_{ij} = [\boldsymbol{U}]_{ij}+\sum_k\sum_l[\mathrm{W}]_{i,j,k,l}[\boldsymbol{X}]_{k,l} [H]ij=[U]ij+k∑l∑[W]i,j,k,l[X]k,l
为了方便表示,我们对下标 ( k , l ) (k,l) (k,l) 进行重新索引,使得 k = i + a , l = j + b k=i+a,l=j+b k=i+a,l=j+b,则可以得到重拍后的权重矩阵 [ V ] i , j , a , b = [ W ] i , j , i + a , j + b [V]_{i,j,a,b}=[\mathrm{W}]_{i,j,i+a,j+b} [V]i,j,a,b=[W]i,j,i+a,j+b。
上式可表述为:
[ H ] i j = [ U ] i j + ∑ a ∑ b [ V ] i , j , a , b [ X ] i + a , j + b [\boldsymbol{H}]_{ij} = [\boldsymbol{U}]_{ij}+\sum_a\sum_b[\mathrm{V}]_{i,j,a,b}[\boldsymbol{X}]_{i+a,j+b} [H]ij=[U]ij+a∑b∑[V]i,j,a,b[X]i+a,j+b
-
平移不变性
现在引入平移不变性,即检测对象在输入 X X X 中的平移应该仅导致隐藏表示 H H H 中的平移。简言之,无须每个像素都要独享一个二维权值张量,所有像素共享同一个即可,故权重张量降为二维即可。此时式子可以简化为:
[ H ] i j = u + ∑ a ∑ b [ V ] a , b [ X ] i + a , j + b [\boldsymbol{H}]_{ij} = u+\sum_a\sum_b[\boldsymbol{V}]_{a,b}[\boldsymbol{X}]_{i+a,j+b} [H]ij=u+a∑b∑[V]a,b[X]i+a,j+b
这就是所谓卷积,使用系数 [ V ] a , b [\boldsymbol{V}]_{a,b} [V]a,b 对 ( i , j ) (i,j) (i,j) 附近的像素 ( i + a , j + b ) (i+a,j+b) (i+a,j+b) 进行加权得到 [ H ] i j [\boldsymbol{H}]_{ij} [H]ij。
-
局部性
对于上述的 a , b a,b a,b 不应该取太大,即范围不应太大,至少不应该是全图。故可将 ∣ a ∣ > Δ ∣ b ∣ > Δ \left|a\right|>\Delta \left|b\right|>\Delta ∣a∣>Δ∣b∣>Δ的范围设置为0(即不考虑范围外的影响)。故可将式子重写为:
[ H ] i j = u + ∑ a Δ ∑ b Δ [ V ] a , b [ X ] i + a , j + b [\boldsymbol{H}]_{ij} = u+\sum_a^\Delta\sum_b^\Delta[\boldsymbol{V}]_{a,b}[\boldsymbol{X}]_{i+a,j+b} [H]ij=u+a∑Δb∑Δ[V]a,b[X]i+a,j+b
至此,可以称 V V V 为卷积核。简言之,卷积操作实际就是计算一圈像素对中间像素的影响,使用不同的卷积核则计算的是不同方面的影响,最终实现提取不同特征的效果。此处参考王木头大佬的视频《从“卷积”、到“图像卷积操作”、再到“卷积神经网络”,“卷积”意义的3次改变》。
6.1.3 卷积
在数学中,卷积被定义为:
( f ∗ g ) ( x ) = ∫ f ( z ) g ( x − z ) d z (f*g)(\boldsymbol{x})=\int f(\boldsymbol{z})g(\boldsymbol{x}-z)d\boldsymbol{z} (f∗g)(x)=∫f(z)g(x−z)dz
用一个例子说明的话,一个不确定的输入函数叠加上一个确定的输出函数,计算最终余量即为卷积。
6.1.4 “沃尔多在哪里”回顾
上面一直将图片作为二维张量,实际上图像一般包含三个通道(即RGB三原色),因此图像应该是一个由高度、宽度和颜色组成的三维张量。故我们应将 X \boldsymbol{X} X 索引为 [ X ] i , j , k [\boldsymbol{X}]_{i,j,k} [X]i,j,k,由此卷积核相应的调整为 [ V ] a , b , c [\boldsymbol{V}]_{a,b,c} [V]a,b,c,再添加一个 d d d 以实现不同通道的输出,即:
[ H ] i , j , d = ∑ a = − Δ Δ ∑ b = − Δ Δ ∑ c [ V ] a , b , c , d [ X ] i + a , j + b , c [\boldsymbol{H}]_{i,j,d} = \sum_{a=-\Delta}^\Delta\sum_{b=-\Delta}^\Delta\sum_c[\boldsymbol{V}]_{a,b,c,d}[\boldsymbol{X}]_{i+a,j+b,c} [H]i,j,d=a=−Δ∑Δb=−Δ∑Δc∑[V]a,b,c,d[X]i+a,j+b,c
练习
(1)假设卷积层式(6.3),覆盖的局部区域 Δ = 0 \Delta=0 Δ=0。在这种情况下,证明卷积核为每组通道独立地实现一个全连接层。
若 Δ = 0 \Delta=0 Δ=0 则意味着卷积核大小为1,那感觉和全连接没区别的哇。
(2)为什么平移不变性可能也不是好主意呢?
太单一,也许不同区域需要的卷积核不一样。
(3)当从图像边界像素获取隐藏表示时,我们需要思考哪些问题?
应该考虑关于填充的事情。
(4)描述一个类似的音频卷积层的架构。
将音频信息转换为二维数据或更高维再进行卷积操作。
(5)卷积层也适合于文本数据吗?为什么?
我觉得可以,只要找到合适的方法数据化文本。因为卷积这种对于特征的提取对于自然语言也应该是适用的。
(6)证明在式(6.6)中, f ∗ g = g ∗ f f*g=g*f f∗g=g∗f。
( f ∗ g ) ( x ) = ∫ f ( z ) g ( x − z ) d z = ∫ f ( x − t ) g ( t ) d ( x − t ) ( 令 t = x − z ) = ∫ g ( t ) f ( x − t ) d t = ( g ∗ f ) ( x ) \begin{align} (f*g)(\boldsymbol{x}) &= \int f(\boldsymbol{z})g(\boldsymbol{x-z})d\boldsymbol{z}\\ &= \int f(\boldsymbol{x-t})g(\boldsymbol{t})d\boldsymbol{(x-t)}\qquad(令 t=\boldsymbol{x-z})\\ &= \int g(\boldsymbol{t})f\boldsymbol{(x-t)}d\boldsymbol{t}\\ &= (g*f)(\boldsymbol{x}) \end{align} (f∗g)(x)=∫f(z)g(x−z)dz=∫f(x−t)g(t)d(x−t)(令t=x−z)=∫g(t)f(x−t)dt=(g∗f)(x)
相关文章:

《动手学深度学习 Pytorch版》 6.1 从全连接层到卷积
6.1.1 不变性 平移不变性(translation invariance): 不管检测对象出现在图像中的哪个位置,神经网络的前面几层应该对相同的图像区域具有相似的反应,即为“平移不变性”。 局部性(locality)&…...

六、数学建模之插值与拟合
1.概念 2.例题和matlab代码求解 一、概念 1.插值 (1)定义:插值是数学和统计学中的一种技术,用于估算在已知数据点之间的未知数据点的值。插值的目标是通过已知数据点之间的某种函数或方法来估计中间位置的数值。插值通常用于数…...

【项目经验】:elementui表格中数字汉字排序问题及字符串方法localeCompare()
一.需求 表格中数字汉字排序,数字按大小排列,汉字按拼音首字母(A-Z)排序。 二.用到的方法 第一步:把el-table-column上加上sortable"custom" <el-table-column prop"date" label"序号…...

Spring Boot的运行原理
Spring Boot的运行原理 Spring Boot是一个用于快速构建独立、可独立运行的Spring应用程序的框架。它通过自动配置和约定优于配置的原则,简化了Spring应用程序的开发过程。下面将详细介绍Spring Boot的运行原理,并附上一些代码解释。 1. 主要组件 Sprin…...

xen-gic初始化流程
xen-gic初始化流程 调试平台使用的是gic-600,建议参考下面的文档来阅读代码,搞清楚相关寄存器的功能。 《corelink_gic600_generic_interrupt_controller_technical_reference_manual_100336_0106_00_en》 《IHI0069H_gic_architecture_specification》…...

Docker从认识到实践再到底层原理(六-1)|Docker容器基本介绍+命令详解
前言 那么这里博主先安利一些干货满满的专栏了! 首先是博主的高质量博客的汇总,这个专栏里面的博客,都是博主最最用心写的一部分,干货满满,希望对大家有帮助。 高质量博客汇总 然后就是博主最近最花时间的一个专栏…...

【Flink】FlinkCDC自定义反序列化器
在我们用FlinkCDC采集mysql数据(或其他数据源)的时候,FlinkCDC输出的格式不标准,不利于我们后续做数据处理,我们通常会使用自定义反序列化器来格式化采集数据方便后续处理 常规的反序列化器如下: public class FlinkDataStreamCDC {public static void main(String[] ar…...

linux基础(2)
目录 一.vi\vim编译器介绍1.三种模式2.vim的使用3.快捷键的使用 二.which,find命令三.grep命令四.wc命令五.管道符六.echo命令1.重定向符 七.tail命令 一.vi\vim编译器介绍 vim\vi是linux中最经典的文本编译器 同图形化界面中的文本编译器是一样的,vi是…...
docker安装zookeeper(单机版)
第一步:拉取镜像 docker pull zookeeper第二步:启动zookeeper docker run -d -e TZ"Asia/Shanghai" -p 2181:2181 -v /home/sunyuhua/docker/zookeeper:/data --name zookeeper --restart always zookeeper...

国际版阿里云/腾讯云免开户:云存储服务:云存储服务能够让你随时随地拜访和同享文件
云存储服务:云存储服务能够让你随时随地拜访和同享文件 云存储服务是一种基于云技术的存储渠道,能够让用户存储、管理和同享各种类型的数据文件,如文档、图片、视频、音频等。这种服务具有许多长处,以下是对其进行的详细分析&…...
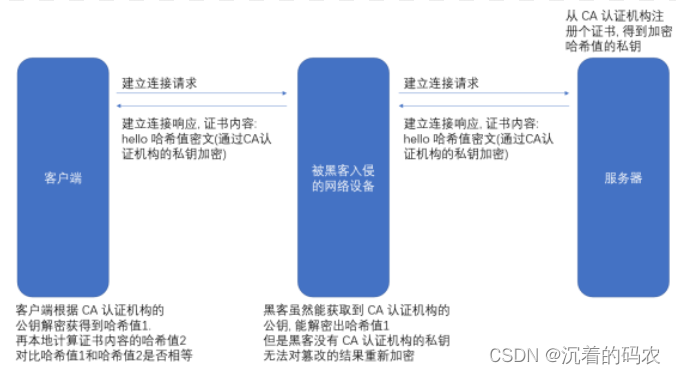
【Java】应用层协议HTTP和HTTPS
HTTP和HTTPS协议 HTTPHTTP协议的工作过程HTTP协议格式抓包工具抓包结果 HTTP请求(Request)URL方法GET方法POST请求其他方法 报头(header)HostContent-lengthContent-TypeUser-AgentRefererCookie 正文(body) HTTP响应HTTP状态码响应报头(header)响应正文(body) 通过form表单构造…...
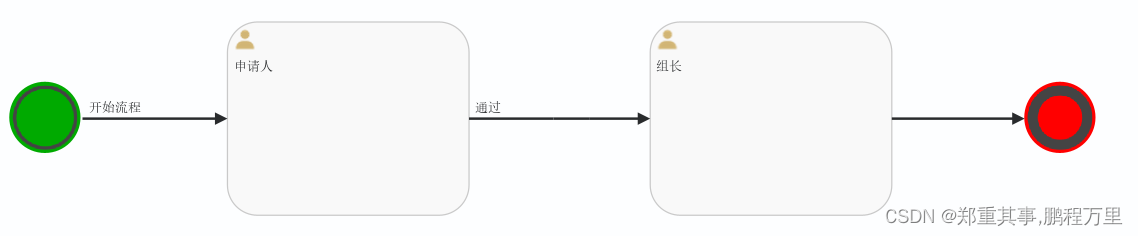
SpringBoot整合Flowable
1. 配置 (1) 引入maven依赖 <dependency><groupId>org.flowable</groupId><artifactId>flowable-spring-boot-starter</artifactId><version>6.7.2</version></dependency><!-- MySQL连接 -->&l…...
华为云香港S3云服务器性能测评_99元一年租用价格
华为云香港S3云服务器1核2G1M带宽99元一年性能测评,配置为S3云服务器1核2G1M带宽,S系列热卖机型,适用于个人建站、普通web应用等负载较低场景,系统盘为高IO40G系统盘,华为云百科分享华为云香港云服务器配置费用&#x…...

prompt 视频收集
1.ChatGPT Prompt提示词工程 ***** 常用技巧 (基本原则,格式,角色扮演)_哔哩哔哩_bilibili...
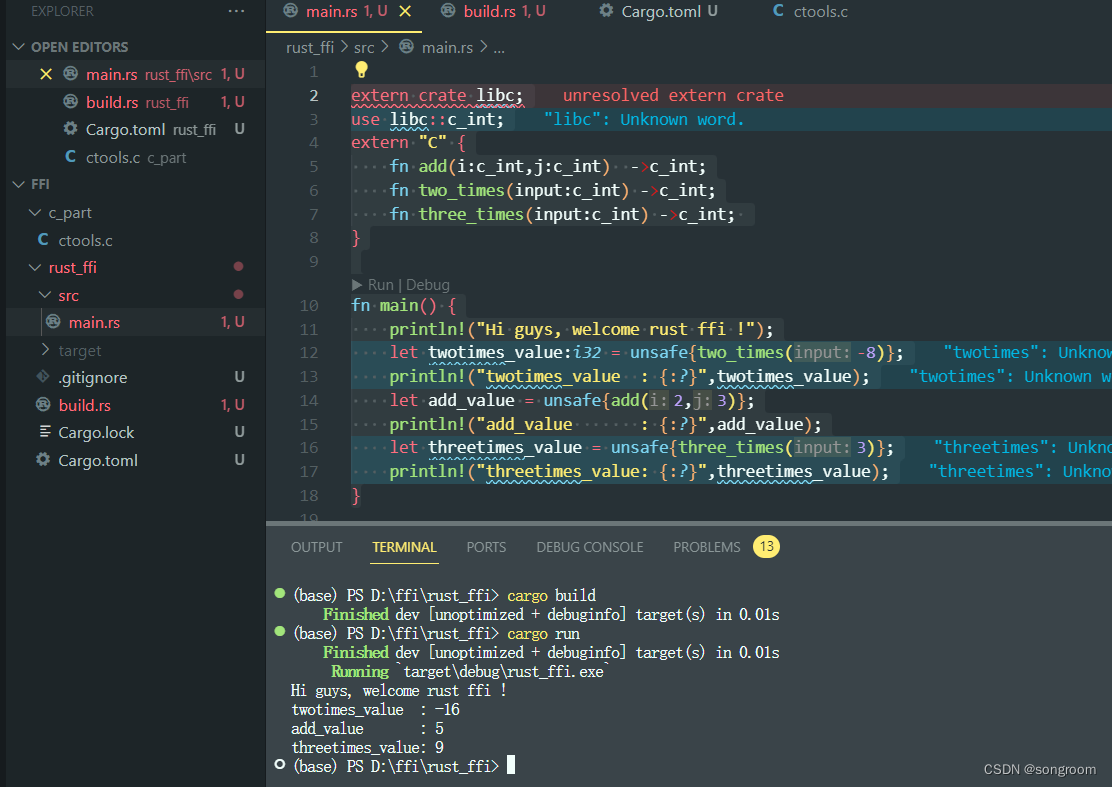
Rust :与C交互
rust调用C端的库函数,有很多方法。今天介绍通过cc库,通过build生成脚本的方式,实现rust调用c端库函数。 1、相关准备: 在ffi目录下,创建了c_part和rust_ffi文件夹。 c_part下放了ctools.c文件,里面有一些…...
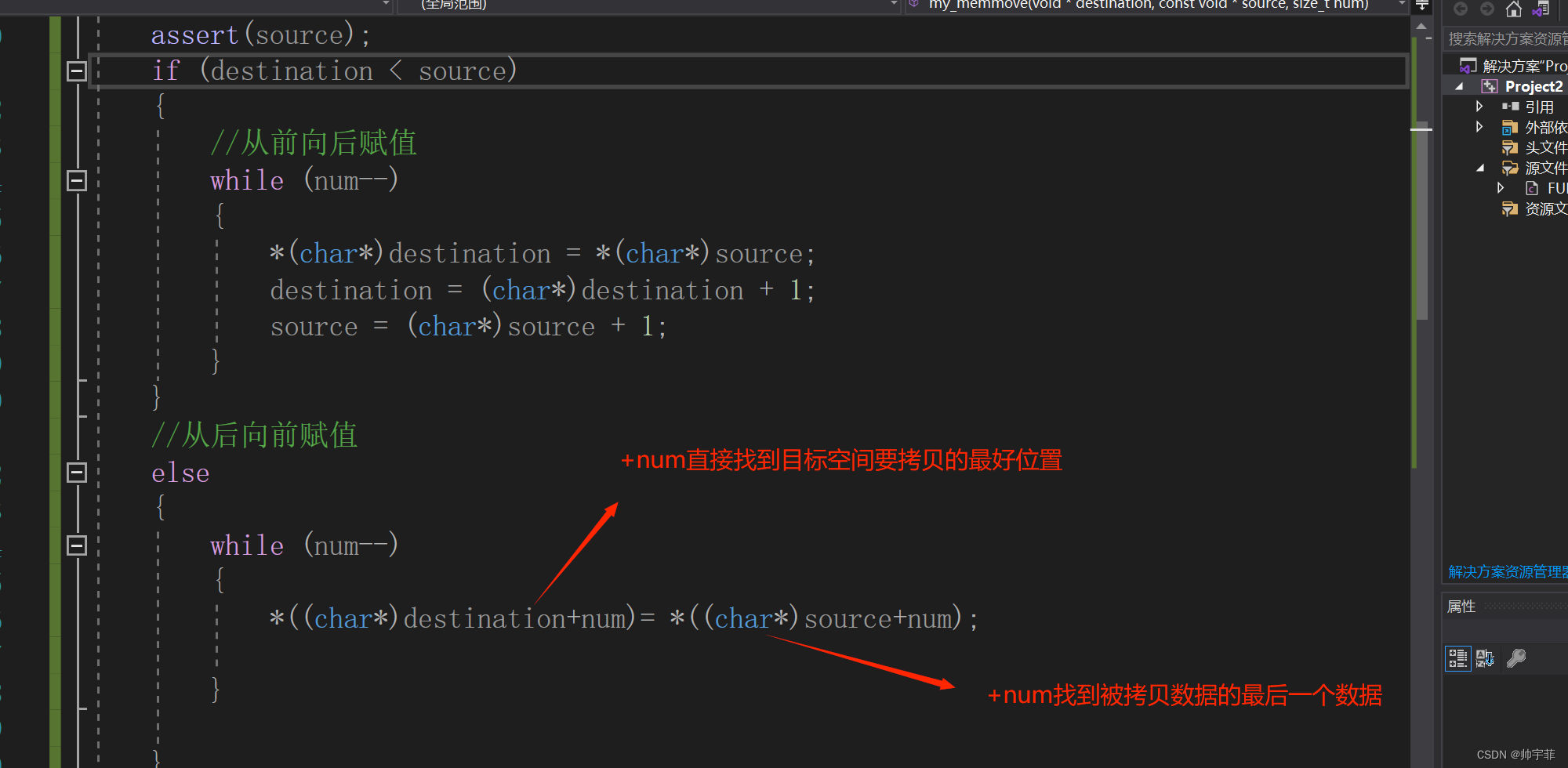
模拟实现C语言--memcpy函数和memmove函数
模拟实现C语言–memcpy函数和memmove函数 文章目录 模拟实现C语言--memcpy函数和memmove函数一、memcpy函数和memmove函数1.1 memcpy函数是什么1.1 memmove函数是什么 二、使用示例2.1 从起始位置复制2.2 从任意位置复制 三、模拟实现3.1 模拟实现1--memcpy函数3.2 针对缺点改进…...

Linux目录
根目录 根目录:“/” 在Linux系统中,根目录指的是整个文件系统的最顶级目录,用符号"/"表示。根目录是文件系统的起点,所有其他目录和文件都嵌套在根目录下面。在根目录下通常会有一些常见的子目录,例如/bin…...
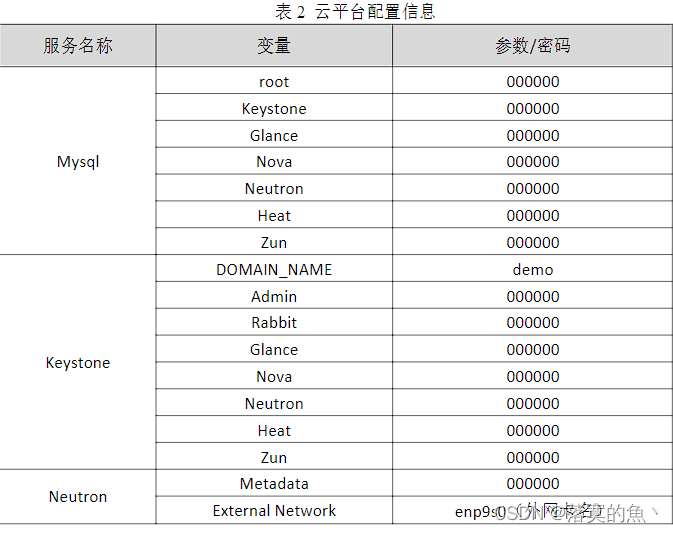
全国职业技能大赛云计算--高职组赛题卷①(私有云)
全国职业技能大赛云计算--高职组赛题卷①(私有云) 第一场次题目:OpenStack平台部署与运维任务1 基础运维任务(5分)任务2 OpenStack搭建任务(15分)任务3 OpenStack云平台运维(15分&am…...

STM32--PWR电源控制
文章目录 PWR电源电源管理器上电复位(POR)和掉电复位(PDR) 可编程电压监测器(PVD)低功耗模式睡眠模式停止模式待机模式 睡眠模式工程停止模式待机模式 PWR STM32的PWR模块是其电源管理系统的核心部分&…...
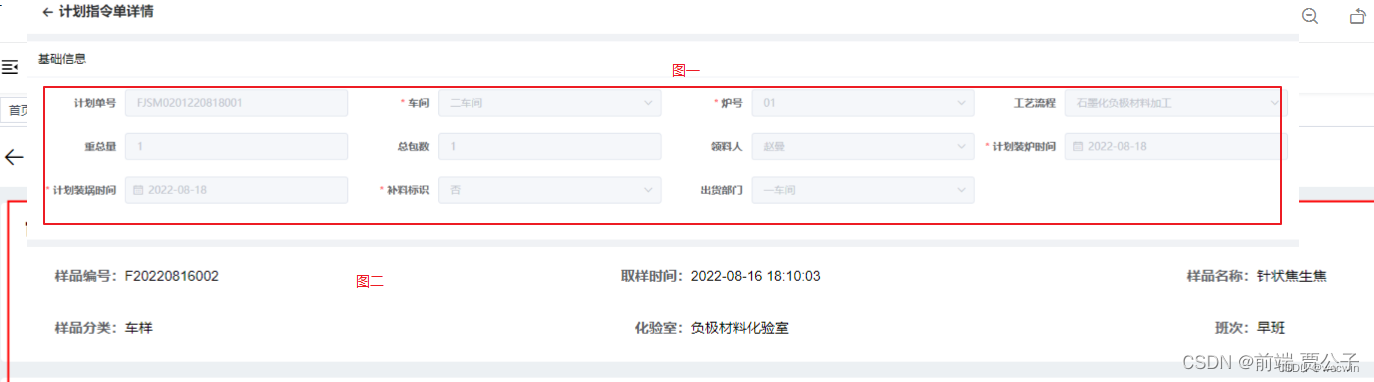
vue+element-ui el-descriptions 详情渲染组件二次封装(Vue项目)
目录 1、需求 2.想要的效果就是由图一变成图二 编辑 3.组件集成了以下功能 4.参数配置 示例代码 参数说明 5,组件 6.页面使用 1、需求 一般后台管理系统,通常页面都有增删改查;而查不外乎就是渲染新增/修改的数据(由输入框变成输…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...

从 GreenPlum 到镜舟数据库:杭银消费金融湖仓一体转型实践
作者:吴岐诗,杭银消费金融大数据应用开发工程师 本文整理自杭银消费金融大数据应用开发工程师在StarRocks Summit Asia 2024的分享 引言:融合数据湖与数仓的创新之路 在数字金融时代,数据已成为金融机构的核心竞争力。杭银消费金…...
)
【LeetCode】3309. 连接二进制表示可形成的最大数值(递归|回溯|位运算)
LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 题目描述解题思路Java代码 题目描述 题目链接:LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 给你一个长度为 3 的整数数组 nums。 现以某种顺序 连接…...

uni-app学习笔记三十五--扩展组件的安装和使用
由于内置组件不能满足日常开发需要,uniapp官方也提供了众多的扩展组件供我们使用。由于不是内置组件,需要安装才能使用。 一、安装扩展插件 安装方法: 1.访问uniapp官方文档组件部分:组件使用的入门教程 | uni-app官网 点击左侧…...
