贪心算法的思路和典型例题
一、贪心算法的思想
贪心算法是一种求解问题时,总是做出在当前看来是最好的选择,不从整体最优上加以考虑的算法。
二.用贪心算法的解题策略
其基本思路是从问题的某一个初始解出发一步一步地进行,根据某个优化测度,每一步都要确保能获得局部最优解。贪心算法的关键在于贪心策略的选择,而不是对所有问题都能得到整体最优解。若下一个数据和部分最优解连在一起不再是可行解时,就不把该数据添加到部分解中,直到把所有数据枚举完,或者不能再添加算法停止。”
三典型题
第五维度
零维是点,点动成线;
一维是线,线动成面;
二维是面,面动成体;
三维是体,体动成史;
四维是史,史动????
现在人类企图理解第五维度。
而小度现在是第五维度的一位智者。一天,小度发现人类的许多科学家在试图理解第五维度,人类是四维生物,若是他们理解了第五维度,很可能也会到来第五维度的空间,这显然是小度不愿意看到的(毕竟哪里都有人口数量的问题….)所以小度希望他们尽可能晚的理解第五维度,因此,小度用更高维度的视角把所有人类中在理解第五维的科学家都看到了,而这些科学家的智商会不一样,所以他们的理解速度 Vi 也会不一样;并且,他们开始理解的时间点 Si 也不一样。理解速度 Vi 描述为每过单位时间可获得 Vi 个单位理解力,也就是说在 Si+1 的时间点该科学家会第一次贡献 Vi 的理解力。我们定义理解力总数超过m 时理解了第五维度。 小度因为维度更高,可以使用时间悖论来给人类一次重大的打击,小度可以让任意一位科学家在任意一个时间点消失,所以他接下来的理解不会继续;而且人类不会记得他,所以他之前的贡献会消失。因为小度能力有限,所以小度只能使用一次暂时悖论。
现在求在尽可能晚的情况下,人类理解第五维度的最早时间点。
时间点初始为00,但显然,没有科学家能够在 00 时刻有贡献。
格式
输入格式:
第一行给出一个整数 n 和一个整数 m ,表示有 n 个科学家,在理解力总数超过 m 时理解了第五维度;
第二至 n+1 行:每行两个整数Si 和 Vi;
对于 100% 的数据:1≤n≤10^5,m≤2∗10^9;
对于 100% 的数据:00≤Si≤2∗10^9,0≤Vi≤10^3。输出格式:
一行,包含一个整数 T 表示在尽可能晚的情况下,人类理解第五维度的最早时间点。
若是人类永远无法理解第五维度,则输出-1。
题解

#include<bits/stdc++.h> using namespace std;
long long s[100000],v[100000],n,m;
bool check(int t){long long sum=0,maxn=-1;for(int i=1;i<=n;i++){if(t-s[i]<=0) continue;sum+=(t-s[i])*v[i];maxn=max(maxn,(t-s[i])*v[i]);}return sum-maxn>m;
}
int main( )
{cin>>n>>m;for(int i=1;i<=n;i++){cin>>s[i]>>v[i];}int l=0,r=999999999;while(l<r){int mid=(l+r)/2;if(check(mid)) r=mid;else l=mid+1;}if(check(1)) cout<<l;else cout<<-1;return 0;
}执行结果:
相关文章:

贪心算法的思路和典型例题
一、贪心算法的思想 贪心算法是一种求解问题时,总是做出在当前看来是最好的选择,不从整体最优上加以考虑的算法。 二.用贪心算法的解题策略 其基本思路是从问题的某一个初始解出发一步一步地进行,根据某个优化测度,每一步都要确保…...

演讲笔记|《一个ppt者的成长故事》
前言:本文为《说服力:工作型PPT该这样做》作者、秋叶PPT团队成员秦阳于2017年1月15日在北京望界无界空间的演讲内容要点总结。 1. 结构化思考(思考能力) 体系:挖多个坑,多个视角(构建体系 – 获…...

【八大经典排序算法】堆排序
【八大经典排序算法】堆排序 一、概述二、思路解读三、代码实现(大堆为例) 一、概述 堆排序是J.W.J. Williams于1964年提出的。他提出了一种利用堆的数据结构进行排序的算法,并将其称为堆排序。堆排序是基于选择排序的一种改进,通…...
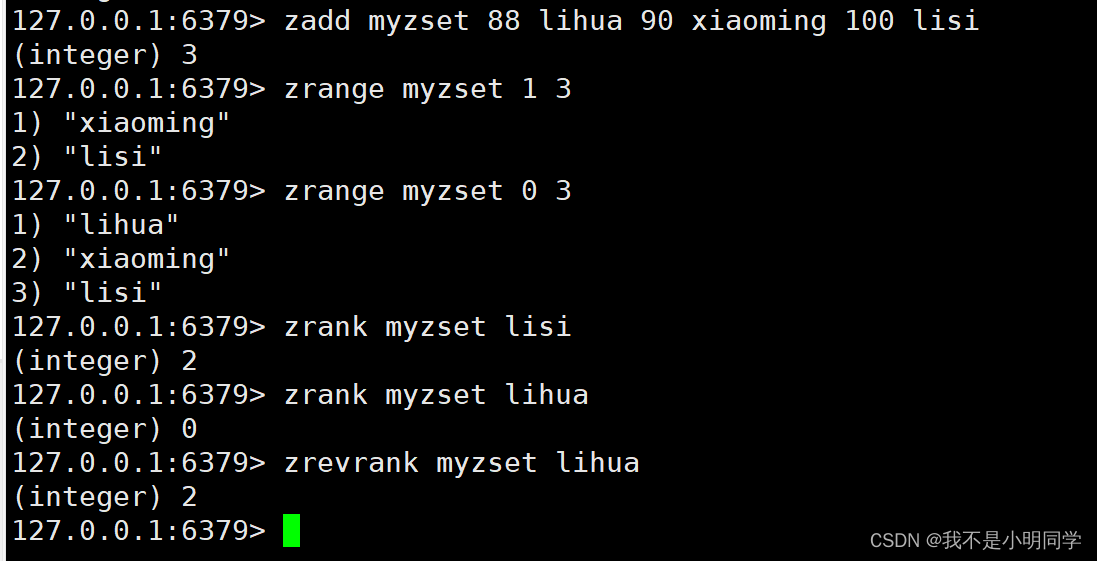
Redis五大基本数据类型
1、字符串类型 字符串类型相当于 java 中的 String 类型。Redis 中的 String 类型以二进制方式存储,不会做任何的编码转换,因此不仅仅可以存储文本数据、整数、普通的字符串、JSON、xml文件,还可以存储图片、视频、音频。String 存储的种类虽…...

AI一点通: OpenAI whisper 在线怎么调用,怎么同时输出时间信息?
OpenAI 语音转文字 whisper API提供了两个端点,即转录和翻译,这基于我们最先进的开源大型v2 Whisper模型。它们可以用来: 将音频转录成音频所在的语言。 翻译并将音频转录成英文。 文件上传目前限制为25 MB,支持以下输入文件类型…...

OpenText EnCase Mobile Investigator 查看、分析和报告被调查手机的证据
OpenText EnCase Mobile Investigator 查看、分析和报告被调查手机的证据 全球83.72%的人口拥有智能手机 OpenText™ EnCase™ Mobile Investigator 使调查人员能够轻松分析、审查和报告与其案件相关的移动设备上的证据。 为什么选择OpenText EnCase Mobile Investigator 预算友…...
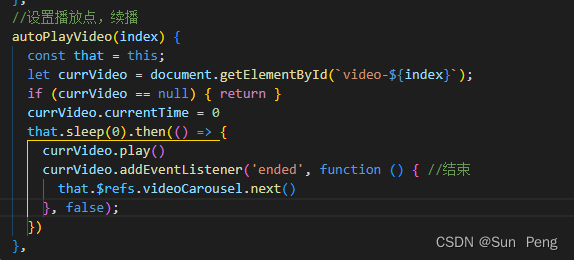
【JavaScript】video标签配置及相关事件:
文章目录 一、标签配置:二、事件:三、案例: 一、标签配置: 标签名描述src要播放的路径地址autoplay是否自动播放,默认值是false,(Boolean)loop是否循环播放,默认值是false,…...

SpringSecurity 初始化解析
文章目录 前言加载SpringSecurity配置解析配置SpringSecurity 解析器security:http 解析FilterChainProxy的注册过程创建 SpringSecurity 过滤器总结 前言 通过上文分析知道了SpringSecurity对一个请求的具体处理流程。不知道大家是否跟我一样都有几个疑问: Filte…...

ip netns网络空间使用
SNAT 源地址转发 执行ip netns exec route_br_ens192_0 iptables -nL POSTROUTING -t nat --line-numbers 输出如下: Chain POSTROUTING (policy ACCEPT) num target prot opt source destination 1 SNAT all -- 0.0.0.0/…...
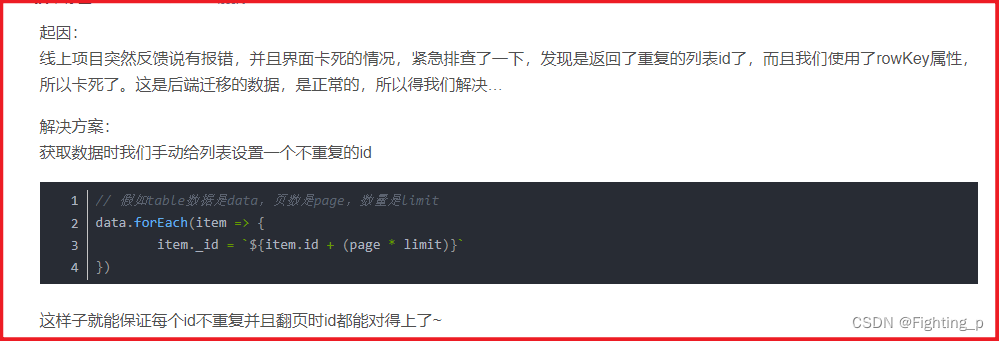
解决 Cannot read property ‘key‘ of undefined
目录 问题解决1解决2最终 问题 现场环境分页查询某些条件项查询时,分页接口获取成功但是数据不渲染,页面像是卡住了: 报错 Cannot read property key of undefined 解决1 有人说 使用的el-pagination在格式化代码的时候layout属性的参数会多加…...

「聊设计模式」之工厂方法模式(Factory Method)
🏆本文收录于《聊设计模式》专栏,专门攻坚指数级提升,助你一臂之力,早日登顶🚀,欢迎持续关注&&收藏&&订阅! 前言 设计模式是指在软件设计中,经过总结和提炼的&#…...
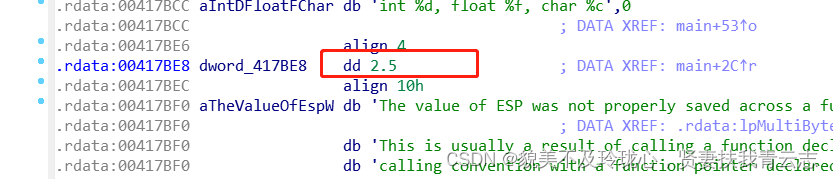
局部变量,全局变量与内存
本文会使用IDA分析局部变量,全局变量在内存的存储 目录 使用IDA分析局部变量 使用IDA分析全局变量 总结 使用IDA分析局部变量 #include <stdio.h>int main() {int nNum 1;float fNum 2.5;char ch A;printf("int %d, float %f, char %c", nNu…...

Python爬虫异常处理实用技巧分享
当我们编写爬虫程序时,经常会遇到各种各样的异常情况,比如网络连接失败、页面解析错误、请求被拒绝等等。这些异常情况可能导致程序中断或者无法正常运行,给我们的数据采集工作带来一定的困扰。所以,掌握一些实用的异常处理技巧对…...
【性能测试】Jmeter —— jmeter计数器
jmeter计数器 如果需要引用的数据量较大,且要求不能重复或者需要递增,那么可以使用计数器来实现 如:新增功能,要求名称不能重复 1,新增计数器 计数器:允许用户创建一个在线程组之内都可以被引用的计数器…...

Python 布尔类型和比较运算符
视频版教程 Python3零基础7天入门实战视频教程 布尔( bool)表达现实生活中的逻辑,即真和假,True表示真,False表示假。 实例: # 布尔类型定义 b1 True b2 False print(f"b1{b1},类型是{type(b1)}") prin…...
蓝牙核心规范(V5.4)10.1-BLE 入门笔记(1)
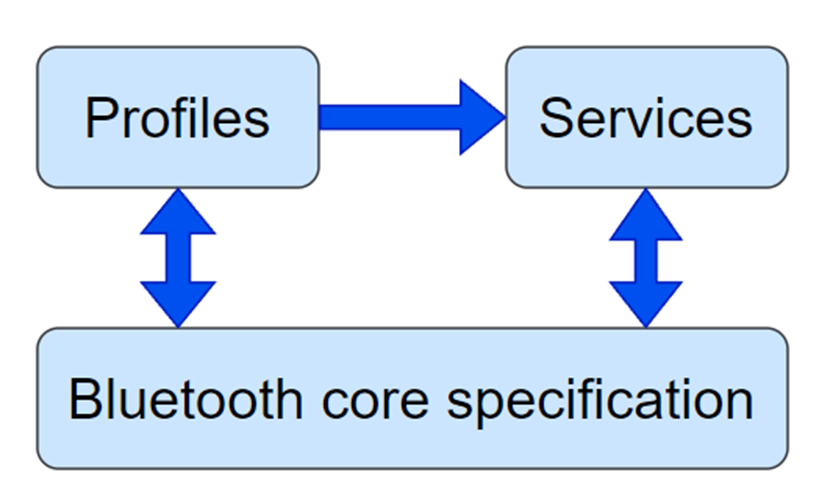
ble 规范 深入了解蓝牙LE需要熟悉相关的规格。蓝牙LE的架构、程序和协议由一项关键规范完全定义,称为蓝牙核心规范。产品如何使用蓝牙以实现互操作性由两种特殊类型称为配置文件和服务的规范集合所涵盖。图1展示了BLE规范类型及其相互关系。 1.1 蓝牙核心规范 蓝牙核心规范是…...

Java高级之泛型、自定义泛型、通配符的使用
泛型与File 文章目录 一、为什么要有泛型?1.1、什么是泛型?1.2、泛型的设计背景1.3、泛型的概念 二、在集合中使用泛型三、自定义泛型结构2.1、泛型方法的使用 四、泛型在继承上的体现五、通配符的使用5.1、通配符的使用5.2、有限制条件的通配符的使用 …...

代码随想录二刷day32
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、力扣122. 买卖股票的最佳时机 II二、力扣55. 跳跃游戏三、力扣45. 跳跃游戏 II 前言 一、力扣122. 买卖股票的最佳时机 II class Solution {public int ma…...

linux基础篇
文章目录 linux基础篇1.Linux文件系统结构:2.常用的Linux指令:3.Shell指令:4.Linux服务管理:5.Linux磁盘挂载:其他 linux基础篇 1.Linux文件系统结构: 根目录 /bin目录:二进制可执行文件存放处boot目录:启…...
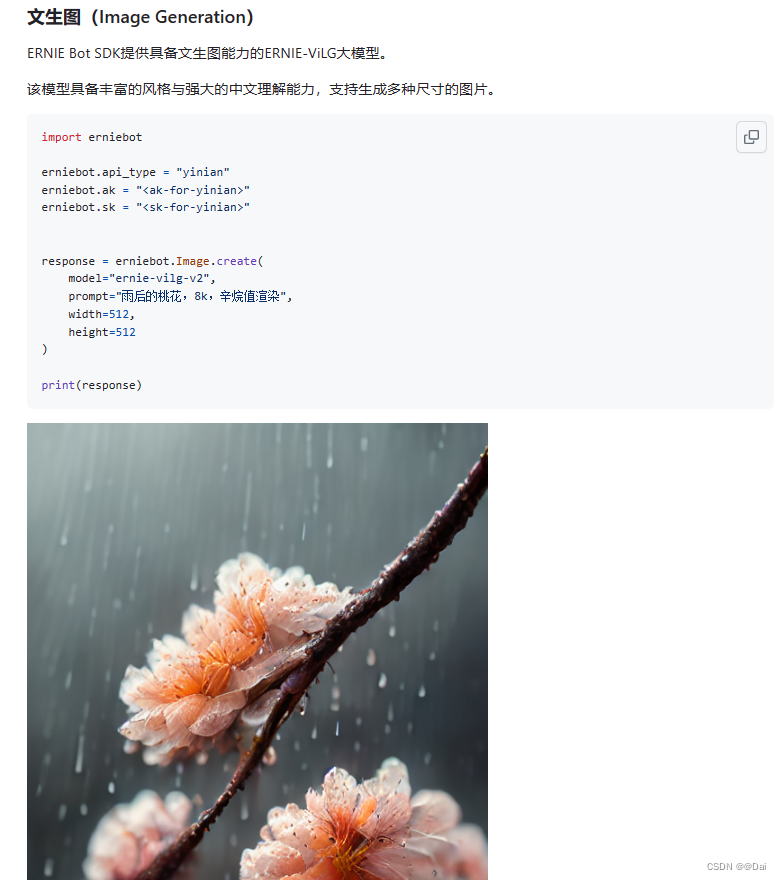
文心一言插件开发全流程,ERNIE-Bot-SDK可以调用文心一言的能力
文心一言插件开发 前言插件插件是什么工作原理申请开发权限 开始第一步:安装python第二步:搭建项目manifest 描述文件:ai-plugin.json插件服务描述文件:openapi.yaml开发自己的plugin-server 第三步:上传插件 SDK相关链…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...

面向无人机海岸带生态系统监测的语义分割基准数据集
描述:海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而,目前该领域仍面临一个挑战,即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...

LangChain知识库管理后端接口:数据库操作详解—— 构建本地知识库系统的基础《二》
这段 Python 代码是一个完整的 知识库数据库操作模块,用于对本地知识库系统中的知识库进行增删改查(CRUD)操作。它基于 SQLAlchemy ORM 框架 和一个自定义的装饰器 with_session 实现数据库会话管理。 📘 一、整体功能概述 该模块…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...
