线性代数的本质(三)——线性方程组
文章目录
- 线性方程组
- 高斯消元法
- 初等行变换
- 线性方程组的解
- 向量方程
- 齐次线性方程组的解
- 非齐次线性方程组的解
线性方程组
高斯消元法
客观世界最简单的数量关系是均匀变化的关系。在均匀变化问题中,列出的方程组是一次方程组,我们称之为线性方程组(Linear system of equations)。 n n n元线性方程组的一般形式为
{ a 11 x 1 + a 12 x 2 + ⋯ + a 1 n x n = b 1 a 21 x 1 + a 22 x 2 + ⋯ + a 2 n x n = b 2 ⋯ ⋯ a m 1 x 1 + a m 2 x 2 + ⋯ + a m n x n = b m \begin{cases} a_{11}x_1+a_{12}x_2+\cdots+a_{1n}x_n=b_1 \\ a_{21}x_1+a_{22}x_2+\cdots+a_{2n}x_n=b_2 \\ \cdots\quad\cdots \\ a_{m1}x_1+a_{m2}x_2+\cdots+a_{mn}x_n=b_m \end{cases} ⎩ ⎨ ⎧a11x1+a12x2+⋯+a1nxn=b1a21x1+a22x2+⋯+a2nxn=b2⋯⋯am1x1+am2x2+⋯+amnxn=bm
如果存在 n n n个常数 x 1 = s 1 , x 2 = s 2 , ⋯ , x n = s n x_1=s_1,x_2=s_2,\cdots,x_n=s_n x1=s1,x2=s2,⋯,xn=sn 满足线性方程组的所有方程,则称为线性方程组的一个解(solution)。方程组的所有解组成的集合称为这个方程组的解集。
解线性方程组的一般方法,是把方程组用一个更容易解的等价方程组 (即有相同解集的方程组)代替。用来化简线性方程组的三种基本变换是:
(1) 互换两个方程的位置;
(2) 把某一个方程的所有项乘以一个非零常数;
(3) 把某一个方程加上另一个方程的常数倍;
以上三种变换称为高斯消元法(Gaussian Elimination)。
例如,解方程组
{ 2 x 2 − x 3 = 7 x 1 + x 2 + 2 x 3 = 0 x 1 + x 2 − x 3 = − 6 x 1 + 3 x 2 − 2 x 3 = 1 \begin{cases} \begin{alignedat}{4} &\quad 2x_2&-\ \ x_3 &= 7 \\ x_1&+\ x_2&+2x_3& = 0 \\ x_1&+\ x_2&-\ \ x_3& = -6 \\ x_1&+3x_2&-2x_3&=1 \end{alignedat} \end{cases} ⎩ ⎨ ⎧x1x1x12x2+ x2+ x2+3x2− x3+2x3− x3−2x3=7=0=−6=1
经过基本变换把线性方程组化成阶梯形方程组
{ x 1 + x 2 − x 3 = − 6 2 x 2 − x 3 = 7 3 x 3 = 6 0 = 0 \begin{cases} \begin{alignedat}{4} x_1&+x_2&-x_3& = -6 \\ &\quad 2x_2&-x_3 &= 7 \\ &\quad &\quad 3x_3& = 6 \\ &\quad &\quad 0& = 0 \end{alignedat} \end{cases} ⎩ ⎨ ⎧x1+x22x2−x3−x33x30=−6=7=6=0
还可以进一步变换为简化阶梯形方程组
{ x 1 = − 9 x 2 = 5 x 3 = 2 0 = 0 \begin{cases} x_1 & & &=-9 \\ & x_2 & & = 5 \\ & & x_3& = 2 \\ & & 0& = 0 \end{cases} ⎩ ⎨ ⎧x1x2x30=−9=5=2=0
上面的简单例子代表了用消元法解线性方程组的一般方法和计算格式。
初等行变换
根据矩阵与向量的乘法定义,线性方程组可写为矩阵形式
A x = b A\mathbf x=\mathbf b Ax=b
其中
A = [ a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋱ ⋮ a m 1 a m 2 ⋯ a m n ] , x = [ x 1 x 2 ⋮ x n ] , b = [ b 1 b 2 ⋮ b n ] A=\begin{bmatrix} a_{11}&a_{12}&\cdots&a_{1n} \\ a_{21}&a_{22}&\cdots&a_{2n} \\ \vdots&\vdots&\ddots&\vdots \\ a_{m1}&a_{m2}&\cdots&a_{mn} \\ \end{bmatrix},\quad \mathbf x=\begin{bmatrix} x_1\\x_2\\\vdots\\x_n \end{bmatrix},\quad \mathbf b=\begin{bmatrix} b_1\\b_2\\\vdots\\b_n \end{bmatrix} A= a11a21⋮am1a12a22⋮am2⋯⋯⋱⋯a1na2n⋮amn ,x= x1x2⋮xn ,b= b1b2⋮bn
矩阵 A A A 称为系数矩阵, x \mathbf x x 为未知数向量, b \mathbf b b 为常数向量。
从上节求解线性方程组的过程中,不难发现,只是对线性方程组的系数和常数项进行了运算。因此,线性方程组可以用它的系数和常数项来求解。
为求解方便,把常数向量添加到系数矩阵最后一列,构成的矩阵
A ˉ = [ A ∣ b ] = [ a 11 ⋯ a 1 n b 1 a 21 ⋯ a 2 n b 2 ⋮ ⋮ ⋱ ⋮ a m 1 ⋯ a m n b m ] \bar A=[A\mid b]=\begin{bmatrix}\begin{array}{ccc:c} a_{11}&\cdots&a_{1n}&b_1 \\ a_{21}&\cdots&a_{2n}&b_2 \\ \vdots&\vdots&\ddots&\vdots \\ a_{m1}&\cdots&a_{mn}&b_m \\ \end{array}\end{bmatrix} Aˉ=[A∣b]= a11a21⋮am1⋯⋯⋮⋯a1na2n⋱amnb1b2⋮bm
称为方程组的增广矩阵(augmented matrix)。
初等行变换:上节所讲的三种基本变换对应于矩阵的下列变换:
(1) 行互换变换:对调矩阵的第 i i i行和第 j j j行 ,记为 r i ↔ r j r_i\lrarr r_j ri↔rj
(2) 行倍乘变换:矩阵的第 i i i行乘以非零常数 k k k,记为 k r i kr_i kri
(3) 行倍加变换:将第 j j j行的元素倍加到第 i i i行,记作 r i + k r j r_i+kr_j ri+krj
称为矩阵的初等行变换(elementary row transformation)。
矩阵消元法:在解线性方程组时,把它的增广矩阵经过初等行变换化成行阶梯形矩阵,写出相应的阶梯形方程组 ,进行求解;或者一直化成简化行阶梯形矩阵,写出它表示的简化阶梯形方程组,从而立即得出解。
上节例子中,增广矩阵经过初等行变换可简化为
A ˉ = [ 0 2 − 1 7 1 1 2 0 1 1 − 1 − 6 1 3 − 2 1 ] → [ 1 1 − 1 − 6 0 2 − 1 7 0 0 3 6 0 0 0 0 ] = B 1 \bar A=\begin{bmatrix}\begin{array}{ccc:c} 0 & 2 & -1 & 7 \\ 1 & 1 & 2 & 0\\ 1 & 1 & -1 & -6 \\ 1 & 3 & -2 & 1 \end{array}\end{bmatrix}\to \begin{bmatrix}\begin{array}{ccc:c} 1 & 1 & -1 & -6 \\ 0 & 2 & -1 & 7\\ 0 & 0 & 3 & 6 \\ 0 & 0 & 0 & 0 \end{array}\end{bmatrix}=B_1 Aˉ= 01112113−12−1−270−61 → 10001200−1−130−6760 =B1
称形如 B 1 B_1 B1 的矩阵为行阶梯形矩阵(Row Echelon Form,REF)。其特点是:
(1) 若有零行(元素全为零的行),零行均在非零行的下方;
(2) 非零行第一个非零元素(称为主元,pivot)以下的元素全为零。
使用初等行变换对行阶梯形矩阵进一步化简
B 1 = [ 1 1 − 1 − 6 0 2 − 1 7 0 0 3 6 0 0 0 0 ] → [ 1 0 0 − 9 0 1 0 5 0 0 1 2 0 0 0 0 ] = B 2 B_1=\begin{bmatrix}\begin{array}{ccc:c} 1 & 1 & -1 & -6 \\ 0 & 2 & -1 & 7\\ 0 & 0 & 3 & 6 \\ 0 & 0 & 0 & 0 \end{array}\end{bmatrix}\to\begin{bmatrix}\begin{array}{ccc:c} 1 & 0 & 0 & -9 \\ 0 & 1 & 0 & 5\\ 0 & 0 & 1 & 2 \\ 0 & 0 & 0 & 0 \end{array}\end{bmatrix}=B_2 B1= 10001200−1−130−6760 → 100001000010−9520 =B2
称形如 B 2 B_2 B2 的矩阵为简化行阶梯形矩阵(Reduced Row Echelon Form,RREF)。其特点是:
(1) 每个非零行主元都是1;
(2) 主元所在列的其他元素都是零。
通过简化行阶梯形矩阵,我们可以直接写出解 x 1 = − 9 , x 2 = 5 , x 3 = 2 x_1=-9,x_2=5,x_3=2 x1=−9,x2=5,x3=2。
使用矩阵消元法,我们可以知道任何矩阵都可以经过有限次初等行变换化成行阶梯形矩阵,任何矩阵也可进一步化成简化行阶梯形矩阵。
从最后的简化行阶梯形矩阵可以直接写出一般解,但注意把自由变量的系数变号移到等式右边。
线性方程组的解
假设某方程组的增广矩阵行已变换为阶梯形矩阵
[ 1 0 − 5 1 0 1 1 4 0 0 0 0 ] \begin{bmatrix}\begin{array}{ccc:c} 1 & 0 & -5 & 1 \\ 0 & 1 & 1 & 4\\ 0 & 0 & 0 & 0 \end{array}\end{bmatrix} 100010−510140
对应的线性方程组是
{ x 1 − 5 x 3 = 1 x 2 + x 3 = 4 0 = 0 \begin{cases} \begin{alignedat}{4} x_1&&-5x_3& = 1 \\ &\quad\ x_2&+x_3 &= 4 \\ &\quad &\quad 0& =0 \end{alignedat} \end{cases} ⎩ ⎨ ⎧x1 x2−5x3+x30=1=4=0
方程组的解可显示表示为 x 1 = 1 + 5 x 3 , x 2 = 4 − x 3 x_1=1+5x_3,\ x_2=4-x_3 x1=1+5x3, x2=4−x3 ,显然有无穷多组解。
把 n n n 元线性方程组的增广矩阵化成行阶梯形矩阵后,若有 r r r 个非零行,则行阶梯形矩阵有 r r r 个主元。以主元为系数的末知量称为主变量,剩下的 n − r n-r n−r 个未知量称为自由变量,其值可任取。
假设某方程组的增广矩阵行已变换为阶梯形矩阵
[ 2 − 3 2 1 0 1 − 4 8 0 0 0 15 ] \begin{bmatrix}\begin{array}{ccc:c} 2 & -3 & 2 & 1 \\ 0 & 1 & -4 & 8\\ 0 & 0 & 0 & 15 \end{array}\end{bmatrix} 200−3102−401815
对应的线性方程组是
{ 2 x 1 − 3 x 2 + 2 x 3 = 1 x 2 − 4 x 3 = 8 0 = 15 \begin{cases} \begin{alignedat}{4} 2x_1&-3x_2&+2x_3& = 1 \\ &\quad\ x_2&-4x_3 &= 8 \\ &\quad &\quad 0& = 15 \end{alignedat} \end{cases} ⎩ ⎨ ⎧2x1−3x2 x2+2x3−4x30=1=8=15
这个阶梯形方程组显然是矛盾的,故原方程组无解。
解的情况:线性方程组有解的充要条件是增广矩阵的增广列不是主元列,即行阶梯形方程组不包含矛盾方程。若线性方程组有解,则解有两种情况:(1) 当没有自由变量时,有唯 一解;(2) 当有自由变量是,有无穷多解。
向量方程
应用向量加法和数乘运算,线性方程组 A x = b A\mathbf x=\mathbf b Ax=b 可以写成向量方程
x 1 a 1 + x 2 a 2 + ⋯ + x n a n = b x_1\mathbf a_1+x_2\mathbf a_2+\cdots+x_n\mathbf a_n=\mathbf b x1a1+x2a2+⋯+xnan=b
其中 a 1 , a 2 , ⋯ , a n \mathbf a_1,\mathbf a_2,\cdots,\mathbf a_n a1,a2,⋯,an 为系数矩阵 A A A 的列向量组, b \mathbf b b 为常数向量。它的一组解 s = ( x 1 , x 2 , ⋯ , x n ) T s=(x_1,x_2,\cdots,x_n)^T s=(x1,x2,⋯,xn)T 称为方程组的解向量。
例如,方程组
{ 2 x 1 − x 2 + x 3 = 4 4 x 1 + 2 x 2 − x 3 = − 1 \begin{cases} \begin{alignedat}{4} 2x_1&-x_2&+x_3& = 4 \\ 4x_1&+2x_2&-x_3& = -1 \end{alignedat} \end{cases} {2x14x1−x2+2x2+x3−x3=4=−1
可以表述为
[ 2 4 ] x 1 + [ − 1 2 ] x 2 + [ 1 − 1 ] x 3 = [ 4 − 1 ] \begin{bmatrix}2\\4\end{bmatrix}x_1+ \begin{bmatrix}-1\\2\end{bmatrix}x_2+ \begin{bmatrix}1\\-1\end{bmatrix}x_3= \begin{bmatrix}4\\-1\end{bmatrix} [24]x1+[−12]x2+[1−1]x3=[4−1]
既然可表示为向量的形式,那么就可以从向量的角度分析。向量方程是否有解的问题等价于判断常数向量 b \mathbf b b 能否由系数矩阵列向量组线性表示,即向量 b \mathbf b b 是否属于系数矩阵的列空间 col A = span { a 1 , a 2 , ⋯ , a n } \text{col }A=\text{span}\{\mathbf a_1,\mathbf a_2,\cdots,\mathbf a_n\} col A=span{a1,a2,⋯,an}。
结论:方程 A x = b A\mathbf x=\mathbf b Ax=b有解的充要条件是 b \mathbf b b 是 A A A 的各列的线性组合。
以线性变换的角度理解,希望找出未知向量 x \mathbf x x ,使得该向量在线性变换 A A A 的作用下变成已知向量 b \mathbf b b。因此,我们可以从逆变换的角度获得未知向量。显然,如果变换后维度压缩,方程不一定有解。即列空间的维度低于未知向量维度。
齐次线性方程组的解
常数项都为零的线性方程组 A x = 0 A\mathbf{x}=0 Ax=0 称为齐次线性方程组。向量方程为
x 1 a 1 + x 2 a 2 + ⋯ + x n a n = 0 x_1\mathbf a_1+x_2\mathbf a_2+\cdots+x_n\mathbf a_n=0 x1a1+x2a2+⋯+xnan=0
齐次线性方程组显然有一组解
x 1 = x 2 = ⋯ = x n = 0 x_1=x_2=\cdots=x_n=0 x1=x2=⋯=xn=0
这组解称为零解或平凡解。除此之外的其他解称为非零解或非平凡解。
方程 A m × n x = 0 A_{m\times n}\mathbf{x}=0 Am×nx=0 有非零解等价于 A A A 的列向量组线性相关,即 rank ( A ) < n \text{rank}(A)<n rank(A)<n
齐次线性方程组的解有如下性质
- 如果 s 1 , s 2 s_1,s_2 s1,s2 是齐次线性方程组的两个解向量,则 s 1 + s 2 s_1+s_2 s1+s2 也是方程组的解向量。
- 如果 s s s 是齐次线性方程组的解向量,则对任意常数 k k k, k s ks ks 也是方程组的解向量。
这两条性质只要直接代入向量方程进行验证就可以。
显然,系数矩阵为 A A A 的齐次线性方程组的解集
ker A = { x ∣ A x = 0 } \ker A=\{\mathbf x|A\mathbf{x}=0\} kerA={x∣Ax=0}
满足向量空间的条件, 称为零空间(nullspace)或核(kernel)。解空间的一组基 s 1 , s 2 , ⋯ , s n − r s_1,s_2,\cdots,s_{n-r} s1,s2,⋯,sn−r 称为该方程组的基础解系。零空间的维数即为自由变量的个数。
如果能找到基础解系,就能描述整个解空间。
定理:
- 方程 A m × n x = 0 A_{m\times n}\mathbf{x}=0 Am×nx=0 有非零解的充要条件是 rank ( A ) < n \text{rank}(A)<n rank(A)<n。
- 方程 A m × n x = 0 A_{m\times n}\mathbf{x}=0 Am×nx=0 基础解系中自由变量的个数等于 n − rank ( A ) n-\text{rank}(A) n−rank(A)。
- 设 A A A 是向量空间 V V V 内的线性变换
dim V = dim ( range A ) + dim ( ker A ) \dim V=\dim(\text{range }A)+\dim(\ker A) dimV=dim(range A)+dim(kerA)
可以用系数矩阵的初等行变换来求基础解系。
示例:求下列齐次线性方程组的解集。
{ x 2 − x 3 + x 4 − x 5 = 0 x 1 + x 3 + 2 x 4 − x 5 = 0 x 1 + x 2 + 3 x 4 − 2 x 5 = 0 2 x 1 + 2 x 2 + 6 x 4 − 3 x 5 = 0 \begin{cases} x_2-x_3+x_4-x_5=0 \\ x_1+x_3+2x_4-x_5=0 \\ x_1+x_2+3x_4-2x_5=0 \\ 2x_1+2x_2+6x_4-3x_5=0 \end{cases} ⎩ ⎨ ⎧x2−x3+x4−x5=0x1+x3+2x4−x5=0x1+x2+3x4−2x5=02x1+2x2+6x4−3x5=0
解:先做矩阵消元法获得阶梯形矩阵和简化阶梯形矩阵
A = [ 0 1 − 1 1 − 1 1 0 1 2 − 1 1 1 0 3 − 2 2 2 0 6 − 3 ] → [ 1 0 1 2 − 1 0 1 − 1 1 − 1 0 0 0 0 1 0 0 0 0 0 ] → [ 1 0 1 2 0 0 1 − 1 1 0 0 0 0 0 1 0 0 0 0 0 ] A=\begin{bmatrix} 0&1&-1&1&-1 \\ 1&0&1&2&-1 \\ 1&1&0&3&-2 \\ 2&2&0&6&-3 \end{bmatrix}\to \begin{bmatrix} 1&0&1&2&-1 \\ 0&1&-1&1&-1 \\ 0&0&0&0&1 \\ 0&0&0&0&0 \end{bmatrix}\to \begin{bmatrix} 1&0&1&2&0 \\ 0&1&-1&1&0 \\ 0&0&0&0&1 \\ 0&0&0&0&0 \end{bmatrix} A= 01121012−11001236−1−1−2−3 → 100001001−1002100−1−110 → 100001001−10021000010
因此
{ x 1 = − x 3 − 2 x 4 x 2 = x 3 − x 4 x 5 = 0 \begin{cases} x_1=-x_3-2x_4 \\ x_2=x_3-x_4 \\ x_5=0 \end{cases} ⎩ ⎨ ⎧x1=−x3−2x4x2=x3−x4x5=0
可写为解向量的形式
[ x 1 x 2 x 3 x 4 x 5 ] = x 3 [ − 1 1 1 0 0 ] + x 4 [ − 2 − 1 0 1 0 ] \begin{bmatrix}x_1 \\ x_2 \\ x_3 \\ x_4 \\ x_5\end{bmatrix}= x_3\begin{bmatrix}-1 \\ 1 \\ 1 \\ 0 \\ 0\end{bmatrix} +x_4\begin{bmatrix}-2\\-1\\0\\1\\0\end{bmatrix} x1x2x3x4x5 =x3 −11100 +x4 −2−1010
非齐次线性方程组的解
对于非齐次线性方程组 A x = 0 A\mathbf{x}=0 Ax=0 。判断向量方程 x 1 a 1 + x 2 a 2 + ⋯ + x n a n = b x_1\mathbf a_1+x_2\mathbf a_2+\cdots+x_n\mathbf a_n=\mathbf b x1a1+x2a2+⋯+xnan=b 是否有解,等价于判断常数向量 b \mathbf b b 是否属于 span { a 1 , a 2 , ⋯ , a n } \text{span}\{\mathbf a_1,\mathbf a_2,\cdots,\mathbf a_n\} span{a1,a2,⋯,an}。
判别定理:线性方程组有解的充要条件是其系数矩阵 A A A与增广矩阵 A ˉ \bar A Aˉ的秩相等 rank ( A ) = rank ( A ˉ ) \text{rank}(A)=\text{rank}(\bar A) rank(A)=rank(Aˉ)。
通俗理解就是,变换后的阶梯形方程组不存在 0 = b 0=b 0=b 的矛盾方程。
解的结构:设 n n n 元非齐次线性方程组 rank ( A ) = rank ( A ˉ ) \text{rank}(A)=\text{rank}(\bar A) rank(A)=rank(Aˉ)
(1) 若 rank ( A ) = n \text{rank}(A)=n rank(A)=n,方程组有唯一解;
(2) 若 rank ( A ) < n \text{rank}(A)<n rank(A)<n,方程组有无穷多解。
非齐次线性方程组 A x = b A\mathbf x=\mathbf b Ax=b 对应的齐次线性方程组 A x = 0 A\mathbf x=0 Ax=0 称为导出方程组。解的关系:
- A x = b A\mathbf x=\mathbf b Ax=b 的任意两个解向量之差是 A x = 0 A\mathbf x=0 Ax=0 的一个解向量;
- A x = b A\mathbf x=\mathbf b Ax=b 的通解是其任一解向量与 A x = b A\mathbf x=\mathbf b Ax=b 通解之和。
如下图
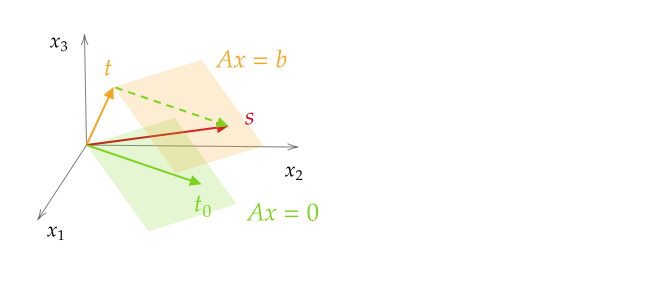
示例:求下列线性方程组的全部解
{ x 1 + 4 x 2 − 5 x 3 = 0 2 x 1 − x 2 + 8 x 3 = 9 \begin{cases} \begin{alignedat}{4} x_1&+4x_2&-5x_3& = 0 \\ 2x_1&-x_2&+8x_3& = 9 \end{alignedat} \end{cases} {x12x1+4x2−x2−5x3+8x3=0=9
解:对方程组的增广矩阵做初等行变换获得阶梯形矩阵和简化阶梯形矩阵
A ˉ = [ 1 4 − 5 0 2 − 1 8 9 ] → [ 1 4 − 5 0 0 − 9 18 9 ] → [ 1 0 3 4 0 1 − 2 1 ] \bar A=\begin{bmatrix}\begin{array}{ccc:c} 1&4&-5&0 \\ 2&-1&8&9 \end{array}\end{bmatrix}\to \begin{bmatrix}\begin{array}{ccc:c} 1&4&-5&0 \\ 0&-9&18&9 \end{array}\end{bmatrix}\to \begin{bmatrix}\begin{array}{ccc:c} 1&0&3&4 \\ 0&1&-2&1 \end{array}\end{bmatrix} Aˉ=[124−1−5809]→[104−9−51809]→[10013−241]
因此
{ x 1 = 4 − 3 x 3 x 2 = 1 + 2 x 3 \begin{cases} x_1=4-3x_3 \\ x_2=1+2x_3 \end{cases} {x1=4−3x3x2=1+2x3
解向量的形式为
[ x 1 x 2 x 3 ] = [ 4 1 0 ] + x 3 [ − 3 2 1 ] \begin{bmatrix}x_1\\x_2\\x_3\end{bmatrix}= \begin{bmatrix}4\\1\\0\end{bmatrix} +x_3\begin{bmatrix}-3 \\ 2 \\ 1 \end{bmatrix} x1x2x3 = 410 +x3 −321
相关文章:
线性代数的本质(三)——线性方程组
文章目录 线性方程组高斯消元法初等行变换线性方程组的解向量方程齐次线性方程组的解非齐次线性方程组的解 线性方程组 高斯消元法 客观世界最简单的数量关系是均匀变化的关系。在均匀变化问题中,列出的方程组是一次方程组,我们称之为线性方程组(Linea…...

轻量级性能测试工具 wrk 如何使用?
项目设计之初或者是项目快要结束的时候,大佬就会问我们,这个服务性能测试的结果是什么,QPS 可以达到多少,RPS 又能达到多少?接口性能可以满足未来生产环境的实际情况吗?有没有自己测试过自己接口的吞吐量&a…...

WebGL 视图矩阵、模型视图矩阵
目录 立方体由三角形构成 视点和视线 视点、观察目标点和上方向 视点: 观察目标点: 上方向: 在WebGL中,观察者的默认状态应该是这样的: 视图矩阵程序(LookAtTriangles.js) 实际上&…...
 方法)
Python 3 – 文件 readline() 方法
Python 3 – 文件 readline() 方法|极客笔记 # 打开文件 file open("example.txt", "r")# 读取文件中的一行数据 line file.readline() while line:# 移除行尾的换行符print(line.strip())# 读取文件中的下一行数据line file.readline()# 关闭文件 file…...
如何在微软Edge浏览器上一键观看高清视频?
编者按:视频是当下最流行的媒体形式之一。但由于视频压缩、网络不稳定等原因,我们常常可以看到互联网上的很多视频其画面质量并不理想,尤其是在浏览器端,这极大地影响了观看体验。不过,近期微软 Edge 浏览器推出了一项…...

Telegram BoT的主流项目盘点
目录 DeFi 类 数据分析类 空投埋伏交易 其他 Telegram Bot赛道的发展趋势预测 Telegram BoT赛道发展较快,具体来看可以分为DeFi 类、数据分析类、空投埋伏交易类以及其他。 DeFi 类 Unibot(交易)、Banana Gun、WagieBot(交…...

PTA 甲级 1044 Shopping in Mars
题目链接 思路:前缀和滑动窗口 #include<bits/stdc.h> #define MAXN 100010 using namespace std; int a[MAXN];int main(){int n,m;cin>>n>>m;//n数量 m金额for(int i1;i<n;i){int t;cin>>t;a[i]a[i-1]t;//前缀和}vector<pair<in…...

Linux学习之MyCat实现分库分表
环境准备 先准备一套MySQL主从服务器,可参考MySQL主从配置配置MyCat服务 资源下载 网盘链接: https://pan.baidu.com/s/1cLTMH_e1-6loc_gF9ZNHTg?pwda63n 提取码: a63n MyCat配置 # 1)安装mycat软件 //安装jdk [rootmycat58 upload]# yum -y insta…...

DirectX12(d3d12)初始化
一、前置要求 Windows 10及以上(安装有DirectX12)VisualStudio 2022 二、DirectX12入门 1.引用头文件 #include<Windows.h> #include<d3d12.h> #include<dxgi1_4.h>2.注册窗口类并初始化窗口 这里我们调用Windows API 通过应用程序的句柄来注册一个唯一…...

算法通关村-----回溯模板如何解决排列组合问题
组合总和 问题描述 给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ,找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ,并以列表形式返回。你可以按 任意顺序 返回这些组合。candidates 中的 同一个 数字可以 无限…...
【1++的C++进阶】之智能指针
👍作者主页:进击的1 🤩 专栏链接:【1的C进阶】 文章目录 一,什么是智能指针二,为什么需要智能指针三,智能指针的发展 一,什么是智能指针 要了解智能指针,我们先要了解RA…...

一百七十九、Linux——Linux报错No package epel-release available
一、目的 在Linux中配置Xmanager服务时,执行脚本时Linux报错No package epel-release available 二、解决措施 (一)第一步,# wget http://dl.fedoraproject.org/pub/epel/epel-release-latest-7.noarch.rpm (二&…...
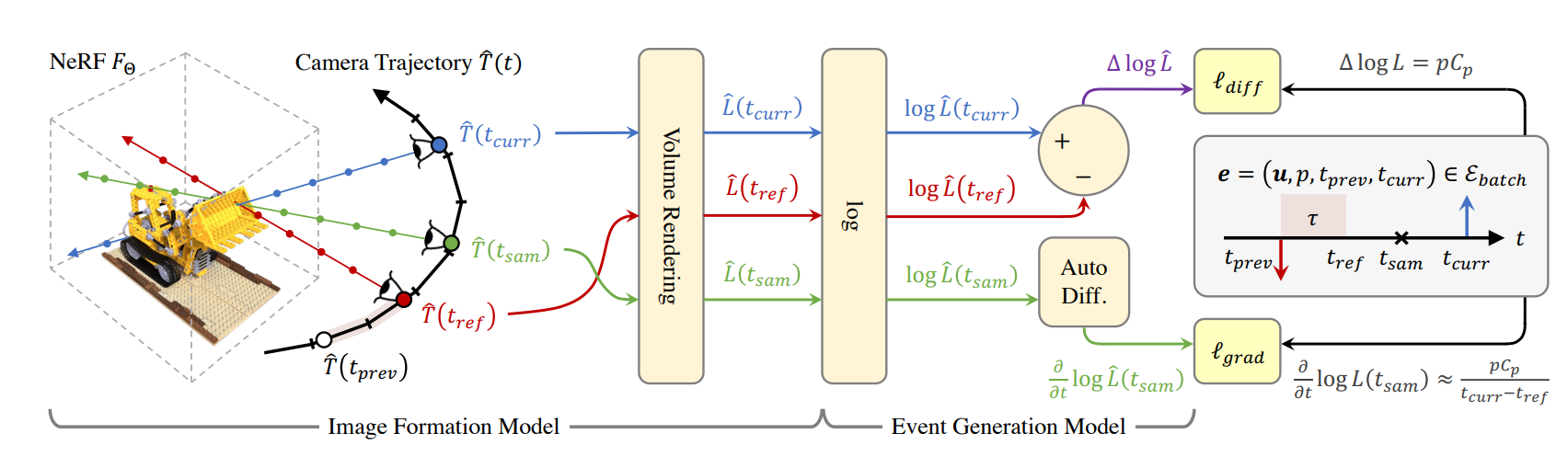
【AI视野·今日CV 计算机视觉论文速览 第248期】Mon, 18 Sep 2023
AI视野今日CS.CV 计算机视觉论文速览 Mon, 18 Sep 2023 Totally 83 papers 👉上期速览✈更多精彩请移步主页 Interesting: 📚Robust e-NeRF,处理高速且大噪声事件相机流的NERF模型。(from NUS新加坡国立) 稀疏噪声事件与稠密事件数据的区别:…...

解决Vue项目中的“Cannot find module ‘vue-template-compiler‘”错误
1. 问题描述 在Vue项目中,当我们使用Vue的单文件组件(.vue文件)时,有时会遇到以下错误信息: ERROR: Cannot find module vue-template-compiler这个错误通常发生在我们使用Vue的版本不匹配或者缺少必要的依赖模块时。…...

tensorflow基础
windows安装tensorflow anaconda或者pip安装tensorflow,tensorflow只支持win7 64系统,本人使用tensorflow1.5版本(pip install tensorflow1.5) tensorboard tensorboard只支持chrome浏览器,而且加载过程中可能有一段…...
spring_注解笔记
spring使用注解开发 文章目录 1.前提1 Bean2 属性注入3 衍生的注解4.自动装配5 作用域 1.前提 步骤1: 要使用注解开发,就必须要保证AOP包的导入 步骤2: xml文件添加context约束 步骤3: 配置注解的支持 <context:annotation-…...
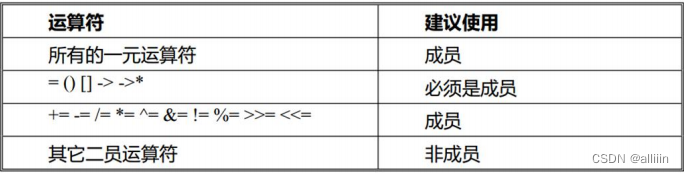
c++运算符重载
目录 运算符重载的基本概念 重载加号运算符() 类内实现 类外实现 运算符重载碰上友元函数 可重载和不可重载的运算符 可重载的运算符 不可重载的运算符 重载自加自减运算符(a a) 智能指针 重载等号运算符() 重载等于和不等运算符(…...

vue子组件向父组件传参的方式
在Vue中,子组件向父组件传递参数可以通过自定义事件和props属性来实现。下面是一些关键代码示例: 1. 使用自定义事件: 在子组件中,通过 $emit 方法触发一个自定义事件,并传递参数。 <template><button cli…...

代码随想录Day41| 343. 整数拆分 |
343. 整数拆分 class Solution { public:int integerBreak(int n) {vector<int> f(n1,0);f[2]1;for(int i3;i<n;i){for(int j1;j<i-1;j){f[i]max(f[i],max(f[i-j]*j,(i-j)*j));}}return f[n];} }; 96. 不同的二叉搜索树 class Solution { public:int numTrees(int…...
)
工厂模式-(简单工厂模式)
首先看一下设计模式的六大原则 设计模式的六大原则 1、开闭原则(Open Close Principle) 开闭原则就是说对扩展开放,对修改关闭。在程序需要进行拓展的时候,不能去修改原有的代码,实现一个热插拔的效果。所以一句话概…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...
