数学建模| 优化入门+多目标规划
优化入门+多目标规划
- 优化入门知识
- 什么是优化问题
- 如何判断是不是优化问题
- 优化模型建模
- 求解器
- 优化问题的分类
- 多目标规划
优化入门知识
什么是优化问题
优化问题:求最优,例如获利最大、最少损失、最短路径、最小化风险等等。
例如:之前文章提到华为杯2019F题多约束条件下智能飞行器航迹快速规划,其中第一问就涉及求飞行器从A点到B点带约束下的最短路径。
如何判断是不是优化问题
题目带有优化、规划、最值、安排、分配、最合理等等。
题目涉及到图,例如三维空间飞行、二维地图上旅行。
优化模型建模
优化模型格式:决策变量+目标函数+约束条件。
决策变量:能够对目标结果产生影响的变量。
x i , i = 1 , 2 , . . . , n x_i,i=1,2,...,n xi,i=1,2,...,n
目标函数:通常都是一个Min或者Max求某个决策变量的函数表达式。例如:
M i n ( o r M a x ) z = f ( x ) , x = ( x 1 , . . . , x n ) T Min(or Max)z=f(x),x=(x_1,...,x_n)^T Min(orMax)z=f(x),x=(x1,...,xn)T
约束条件:以s.t.为开头,后面写上约束条件。
s . t . { g 1 ( x ) ⩽ 0 g 2 ( x ) ⩽ 0 . . . g n ( x ) ⩽ 0 s.t. \begin{cases} g_1(x)\leqslant0\\ g_2(x)\leqslant0\\ ...\\ g_n(x)\leqslant0\\ \end{cases} s.t.⎩ ⎨ ⎧g1(x)⩽0g2(x)⩽0...gn(x)⩽0
求解器
优化模型建立好之后,选择什么样的算法去解模型是比赛的关键。
求解器:用来求解模型的程序、算法之类的,在matlab里面求解器填写的其实就是函数模型。
优化问题的分类
从目标函数的个数来说:可以分成单目标和多目标。
从问题的类型来说:可以分为规划类、图论和动态规划。
规划类按照决策变量在目标函数和约束条件中是否线性:可以分为线性规划和非线性规划。
规划类中,比较特殊的是决策变量为整数的“整数规划”,和决策变量只能取0或者1的“0-1规划”。
非线性规划中比较特殊的是二次规划,目标函数是关于决策变量的二次函数,约束条件是线性函数。
图论中常见的问题有:最短路、最小生成树、网络流和排队论。
多目标规划
条件:线性规划和非线性规划只有一个目标函数,多目标函数有多个目标函数( f i ( x ) f_{i}(x) fi(x)),讲究一个既要还要。
方法:多目标转化为单目标。
- 优先因子:可以主观上给目标函数进行一个重要性排序,来使得整体的完成情况尽量好,也就是优先因子,相当于权重( P i P_i Pi)。
m i n ∑ P i f i ( x ) min\sum P_{i}f_{i}(x) min∑Pifi(x) - 平方加权:知道每个目标理想值的情况下,可以求每个目标函数和理想值的平方和,可以带上权重。
m i n ∑ λ i [ f i ( x ) − f i ∗ ] 2 min\sum \lambda_{i}[f_{i}(x)-{f_i}^*]^2 min∑λi[fi(x)−fi∗]2 - 乘除法:如果每个目标重要程度一样。
m i n f 1 ( x ) f 2 ( x ) . . . f k ( x ) f k + 1 ( x ) f k + 2 ( x ) . . . f n ( x ) min\frac{f_{1}(x)f_{2}(x)...f_{k}(x)}{f_{k+1}(x)f_{k+2}(x)...f_{n}(x)} minfk+1(x)fk+2(x)...fn(x)f1(x)f2(x)...fk(x) - 分开求最优解对比:有时候单独最优解之间差距可能不是很大,例如之前华为杯2019F题,有个论文就是分别求最优路径和最少矫正点,然后对比。
特殊:问题中存在刚性约束和柔性约束。刚性约束就是必须要满足的,否者就是不可行解。柔性约束就是可以存在偏差的,例如使目标f(x)尽可能不少于5,可以在5左右有正负偏差。这个正负偏差可以记作 d + 和 d − d^+和d^- d+和d−, d + = m i n { f ( x ) − f ∗ , 0 } , d − = − m i n { f ∗ − f ( x ) , 0 } d^+=min\{f(x)-f^*,0\},d^-=-min\{f^*-f(x),0\} d+=min{f(x)−f∗,0},d−=−min{f∗−f(x),0}。
例子:三个目标函数 f 1 ( x ) 、 f 2 ( x ) 、 f 3 ( x ) f_1(x)、f_2(x)、f_3(x) f1(x)、f2(x)、f3(x),三个目标是柔性约束,1尽量不超过、2尽量等于、3尽量不少于,会发现柔性约束都有“尽量”两个字作为修饰。最终的多目标规划函数可以写成:
min { P 1 d 1 + + P 2 ( d 2 − + d 2 + ) + P 3 d 3 − } \min{\{P_1{d_1}^++P_2({d_2}^-+{d_2}^+)+P_3{d_3}^-\}} min{P1d1++P2(d2−+d2+)+P3d3−}
扩展一下格式:
m i n ∑ P i ( w i + d i + + w i − d i − ) min\sum {P_i({w_{i}}^+{d_{i}}^++{w_{i}}^-{d_{i}}^-)} min∑Pi(wi+di++wi−di−)
总结:多目标规划,可以转换成为单目标问题,然后单目标去看符合单目标中那种取套,根据情况套回规划类、图论和动态规划中。
相关文章:

数学建模| 优化入门+多目标规划
优化入门多目标规划 优化入门知识什么是优化问题如何判断是不是优化问题优化模型建模求解器优化问题的分类 多目标规划 优化入门知识 什么是优化问题 优化问题:求最优,例如获利最大、最少损失、最短路径、最小化风险等等。 例如:之前文章提…...

SSM整合Thymeleaf时,抽取公共页面并向其传递参数
第一步 创建一个名为 header.html 的公共头部页面模板,放在 WEB-INF 目录下的 common 文件夹中。在 header.html 中可以编写头部页面的HTML代码,并通过Thymeleaf的语法来接收参数,如下所示: <!DOCTYPE html> <html xml…...

接口测试 —— requests 的基本了解
● requests介绍及安装 ● requests原理及源码介绍 ● 使用requests发送请求 ● 使用requests处理响应 ● get请求参数 ● 发送post请求参数 ● 请求header设置 ● cookie的处理 ● https证书的处理 ● 文件上传、下载 requests介绍 ● requests是python第三方的HTT…...

2023年华为杯数学建模研赛D题思路解析+代码+论文
下文包含:2023华为杯研究生数学建模竞赛(研赛)D题思路解析代码参考论文等及如何准备数学建模竞赛(22号比赛开始后逐步更新) C君将会第一时间发布选题建议、所有题目的思路解析、相关代码、参考文献、参考论文等多项资…...
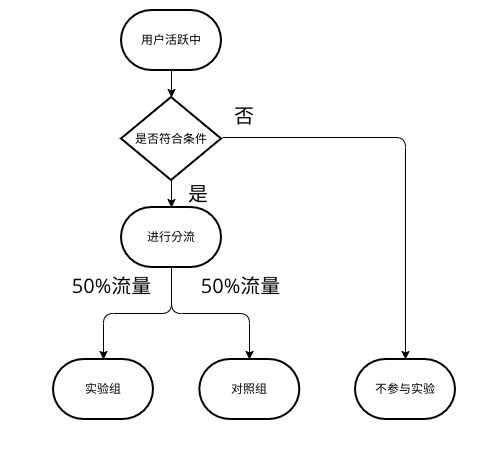
AB试验(三)一次试验的规范流程
AB试验(三)一次试验的规范流程 一次完整且规范的A/B试验可参考下图: 确定目标和假设 核心:A/B测试是因果推断,所以我们首先要确定原因和结果。目标决定了结果,而假设又决定了原因。 如何确定 分析问题&am…...
ROI tracking by using OpenCV
目录 source code: source code: import cv2tracker cv2.TrackerKCF_create() video cv2.VideoCapture(1)while True:ret,frame video.read()cv2.imshow("source frame",frame)k cv2.waitKey(30)if k q:break bbox cv2.selectROI(frame, False) ok tracker.i…...

(leetcode)二叉树最大深度
个人主页:Lei宝啊 愿所有美好如期而遇 目录 题目: 思路: 代码: 图解: 题目: 给定一个二叉树 root ,返回其最大深度。 二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数…...
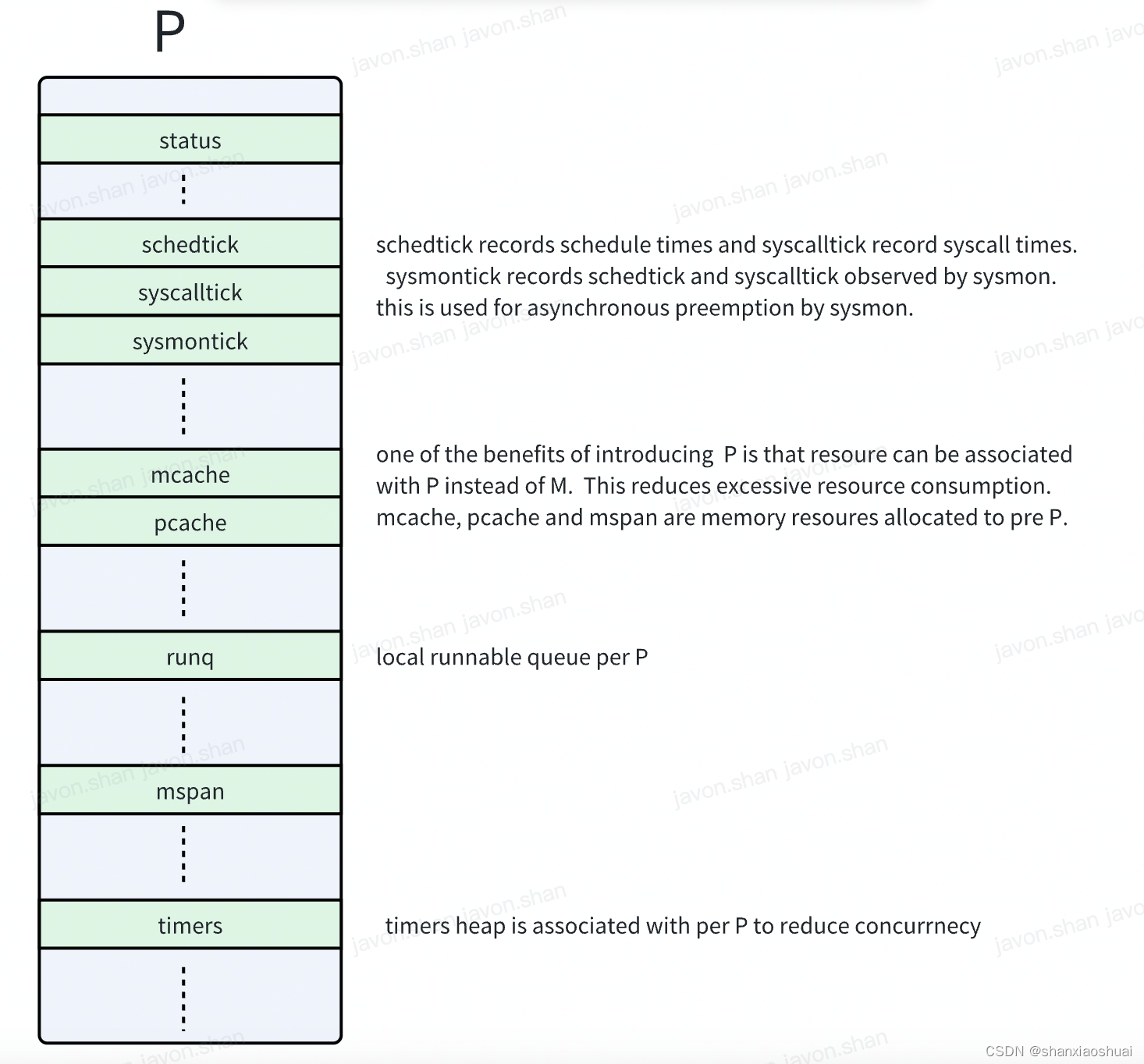
【golang】调度系列之P
调度系列 调度系列之goroutine 调度系列之m 在前面两篇中,分别介绍了G和M,当然介绍的不够全面(在写后面的文章时我也在不断地完善前面的文章,后面可能也会有更加汇总的文章来统筹介绍GMP)。但是,抛开技术细…...

Vue3中watch用法
在 Vue3 中的组合式 API 中,watch 的作用和 Vue2 中的 watch 作用是一样的,他们都是用来监听响应式状态发生变化的,当响应式状态发生变化时,都会触发一个回调函数。 当需要在数据变化时执行异步或开销较大的操作时,com…...

组里来了一个实习生,一行代码引发了一个惨案
大家好,我是静幽水,一名大厂全栈程序员,今天给大家分享一个案例,看似简单。却容易引发惨案。 事情是这样的,最近组里来了一个实习生,因为项目工作量大,人力比较紧张,所以就分配了一…...

随手笔记(四十五)——idea git冲突
图片为引用,在一次导入项目至gitee的过程中,不知道为什么报了403,很奇怪的一个错误,网上很多的答案大概分成两种。 第一种是最多的,直接找到windows凭据删掉 很抱歉的告诉各位,你们很多人到这里就已经解…...

chacha20 算法流程
chacha20算法请参看 RFC:7539。下面是我的理解,欢迎指正。 chacha20算法的基本思想:加密时,将明文数据与用户之间约定的某些数据进行异或操作,得到密文数据;由异或操作的特点可知,在解密时,只需…...
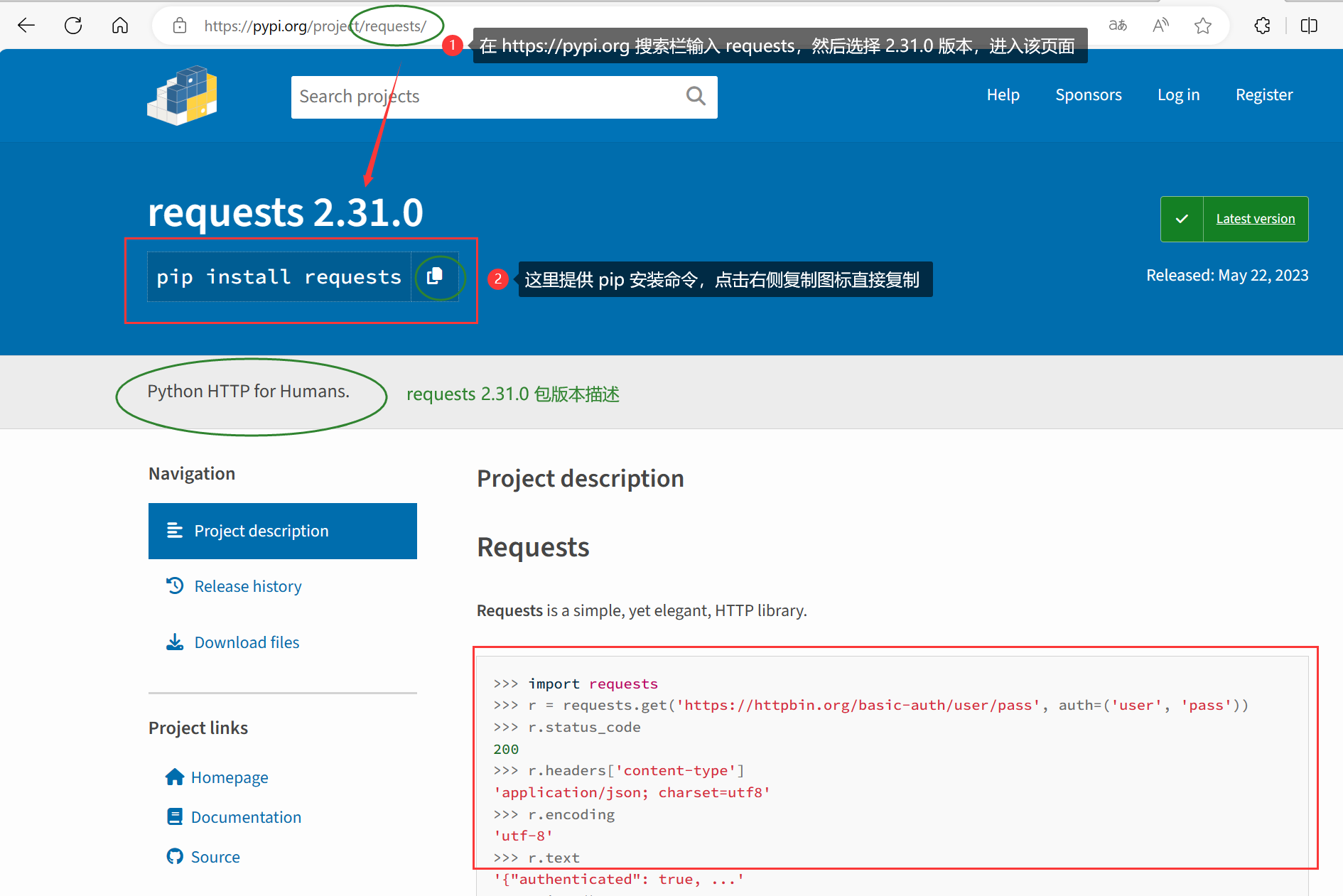
准备篇(三)Python 爬虫第三方库
第三方库无法将 "pip" 识别ModuleNotFoundError: No module named pip install 安装路径相关问题requests 库和 BeautifulSoup 库requests 库BeautifulSoup 库第三方库 Python 的 标准库 中提供了许多有用的模块和功能,如字符串处理、网络通信、多线程等,但它们并…...

从零开始的PICO开发教程(4)-- VR世界 射线传送、旋转和移动
从零开始的PICO开发教程(4)-- VR世界 射线传送、旋转和移动 文章目录 从零开始的PICO开发教程(4)-- VR世界 射线传送、旋转和移动一、前言1、大纲 二、VR射线移动功能实现与解析1、区域传送(1)新建 XR Orig…...
防止攥改之水印功能组件
防止攥改之水印功能组件 效果图逻辑代码 效果图 逻辑代码 <template><div class"containerBox" ref"parentRef" style"height: 300px;background-color: red;"><slot></slot></div> </template><script…...

iOS 17 适配 Xcode 15 问题
在适配 iOS 17 xcode 15时遇到的问题,记录一下。 1、 Could not build module ‘WebKit’ type argument nw_proxy_config_t (aka struct nw_proxy_config *) is neither an Objective-C object nor a block type解决方案: 选中不能编译的库的xcodep…...

Element Plus 快速开始
1.完整引入(全局引入) // main.ts import { createApp } from vue import ElementPlus from element-plus import element-plus/dist/index.css import App from ./App.vueconst app createApp(App)app.use(ElementPlus) app.mount(#app) npm install e…...
华为云云耀云服务器L实例评测|StackEdit中文版在线Markdown笔记工具
华为云云耀云服务器L实例评测|StackEdit中文版在线Markdown笔记工具 一、云耀云服务器L实例介绍1.1 云服务器介绍1.2 应用场景1.3 支持镜像 二、云耀云服务器L实例配置2.1 重置密码2.2 服务器连接2.3 安全组配置 三、部署 StackEdit 中文版3.1 StackEdit 介绍3.2 环…...

MyEclipse报错javax/persistence/EntityManagerFactory
MyEclipse报错: Build path is incomplete. Cannot find class file for javax/persistence/EntityManagerFactory 解决方案: 引入依赖 <dependency><groupId>javax.persistence</groupId> <artifactId>persistence-api</a…...

【MySQL进阶】SQL性能分析
一、SQL性能分析 1.SQL执行频率 MySQL 客户端连接成功后,通过 show [session|global] status 命令可以提供服务器状态信 息。通过如下指令,可以查看当前数据库的 INSERT 、 UPDATE 、 DELETE 、 SELECT 的访问频次: -- session 是查看当…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...
