双指针 (C/C++)
1. 双指针
双指针算法的核心思想:将暴力解法的时间复杂度,通常是O(N*N),通过某种特殊的性质优化到O(N)。
做题思路:先想想暴力解法的思路,然后分析这道题的特殊性质,一般是单调性。然后得出双指针算法的思路。
双指针算法的模板:
for(int i = 0; i <n; i++)
{
while(j < i && check(i, j))
j++;
//具体题目的解题思路
}、
1.1 例题
给定一个长度为 n 的整数序列,请找出最长的不包含重复数数字的最长子序列,输出它的长度。
输入格式
第一行包含整数 n 。
第二行包含 n 个整数(均在0 ~ 100000范围内),表示整数序列。
输出格式
共一行,包含一个整数,表示最长的不包含重复数字的连续子序列的长度。
数据范围
1 <= n <= 100000
按照上面介绍的解题思路:我们先看看暴力解法怎么做的:两层for循环,外层循环在遍历数组时,对于外层循环遍历的每一个值,内层循环都会从该位置开始去遍历,通过检查区间内是否存在重复数字,更新结果。显然这种解法的事件复杂度为O(N*N)。伪代码如下:
for (int i = 0; i < n; i++)
{
for (j = i + 1; j < n; j++)
{
if (!check(i, j))
ret = max(ret, i - j + 1);
}
}其中n为数组的长度,check为检查区间 [ i, j ] 中的元素是否存在重复的数字,如果不存在更新结果,保存到ret中。
双指针:同样根据上面提供的解题思路,我们尝试从暴力解法中分析出单调性。嗯,双指针的左侧指针在整个查找过程中是单调的。怎么理解呢?
下面以一个具体的例子:1,2,2,3,5 来分析哈:
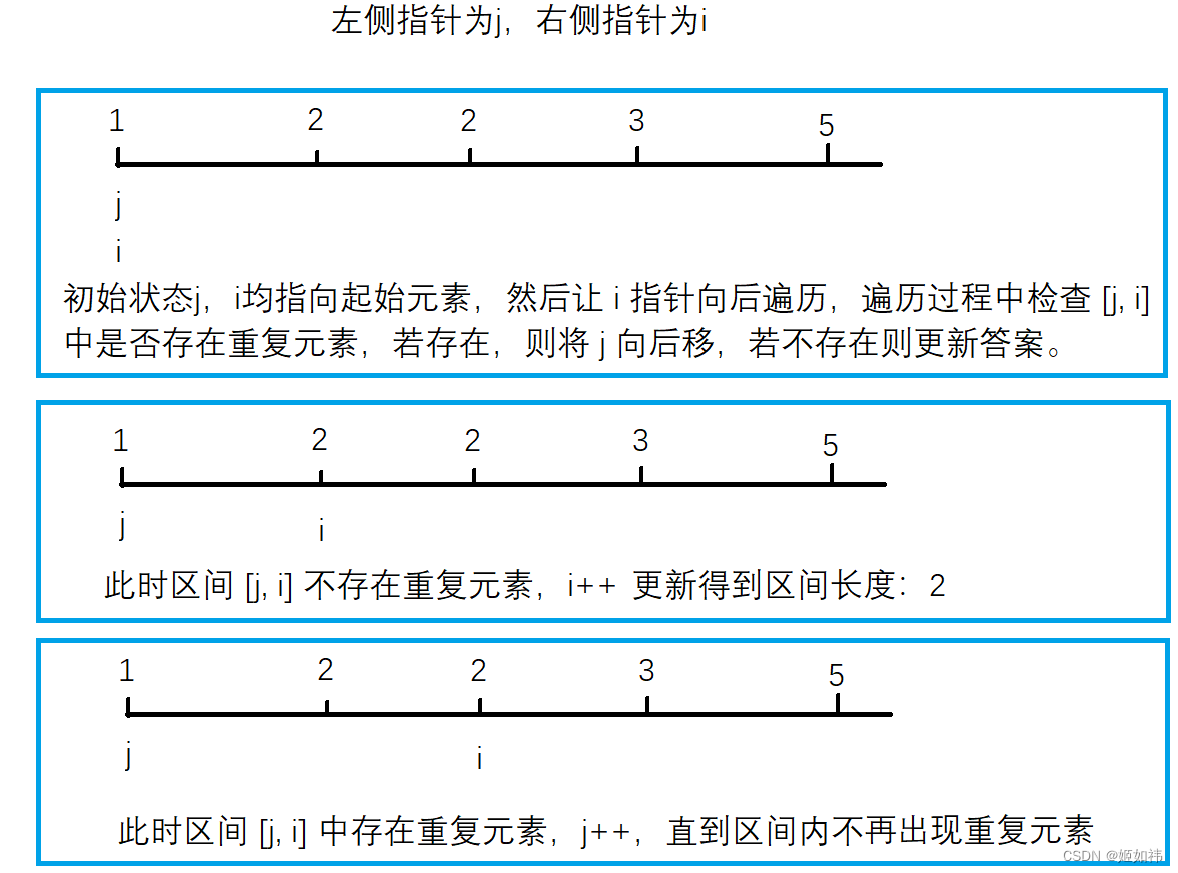

现在我们已经知道了双指针的大致思路了,但是好像还没有弄清除单调性从何而来。对于本题单调性就是:在 i++ 向右找更大的满足要求的更长区间时,j不可能存在向前动 (j--) 的情况。即,本题中 j 具有单调性。
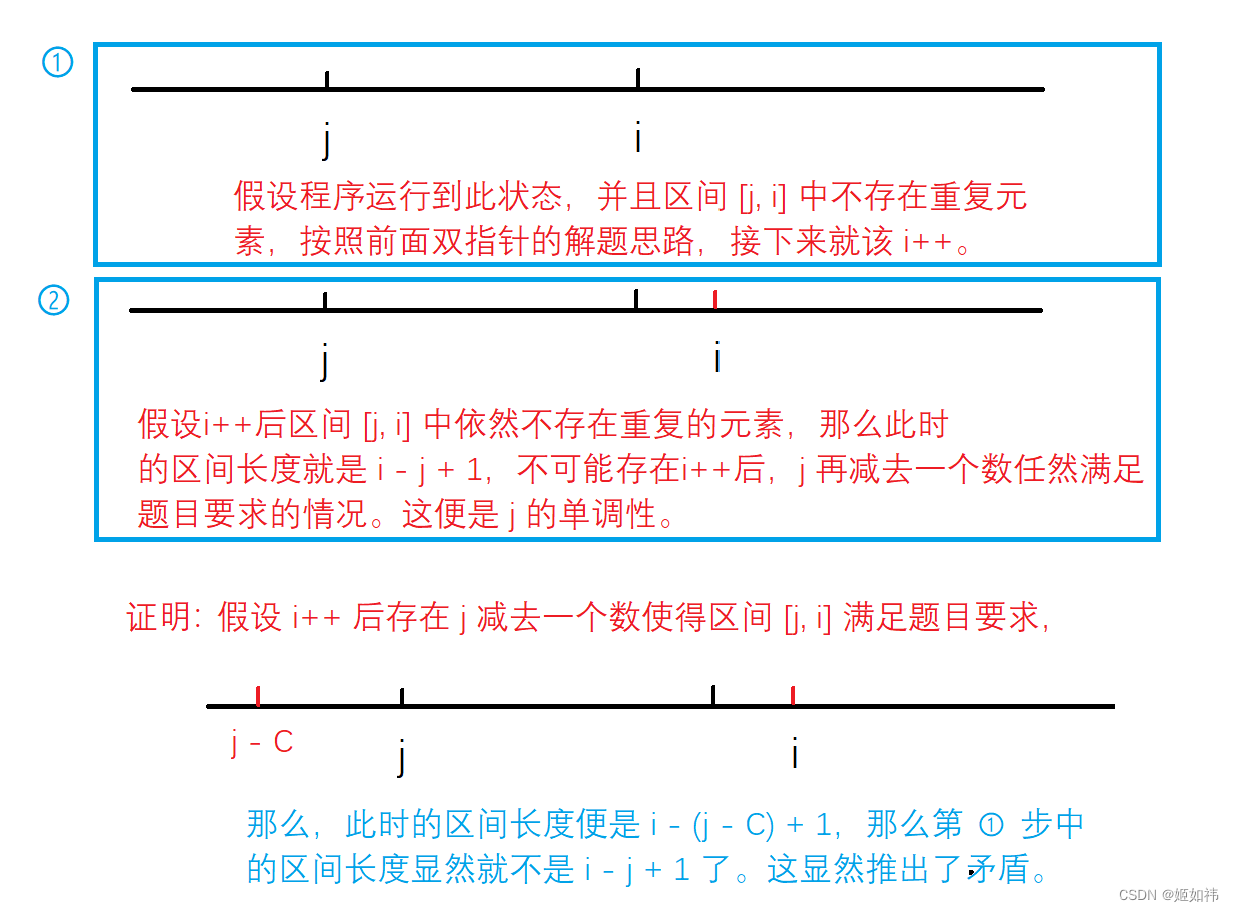
弄清除了这些,我们只需要知到怎么判定一个区间中是否有重复元素就行了。我们可以初始化一个数组a,遍历原数组b, 得到的值假设为s,就让 a[s] + 1,代表这个数字出现了一次。注意当一个区间中没有重复元素时,i++,那么只有原数组中下标为 i 的 的值才会是重复的元素,因此我们只需要判断 a[b[i]] 的值是否是大于 1 即可。这就是模板中的 check 。另外本题中不要 i > j 这个条件,因为 i == j 时,区间 [j, i] 中就没有重复的元素了,i然后就会加一,即 j 是不会大于 i 的。
当区间内存在重复元素时,j++的同时要将 a[b[j]]--,少了一个数字嘛。

现在可以写代码啦!
int main()
{const int N = 100000;//原数组int b[N];//统计数字出现次数的数组int a[N] = { 0 };//用于保存最大的区间长度int ret = 0;int j = 0;//读入数据int n;scanf("%d", &n);for (int i = 0; i < n; i++){scanf("%d", &b[i]);}//核心算法for (int i = 0; i < n; i++){a[b[i]]++;while (a[b[i]] > 1){//少一个数字,次数减一a[b[j]]--;j++;}//更新结果ret = ret > i - j + 1 ? ret : i - j + 1;}//打印结果printf("%d\n", ret);system("pause");return 0;
}1.2 小试牛刀(来源:Acwing)

相关文章:

双指针 (C/C++)
1. 双指针 双指针算法的核心思想:将暴力解法的时间复杂度,通常是O(N*N),通过某种特殊的性质优化到O(N)。 做题思路:先想想暴力解法的思路,然后分析这道题的特殊性质,一般是单调性。然后得出双指针算法的思路…...
CVE-2023-23752 Joomla未授权访问漏洞分析
漏洞概要 Joomla 在海外使用较多,是一套使用 PHP 和 MySQL 开发的开源、跨平台的内容管理系统(CMS)。 Joomla 4.0.0 至 4.2.7 版本中的 ApiRouter.php#parseApiRoute 在处理用户的 Get 请求时未对请求参数有效过滤,导致攻击者可向 Joomla 服务端点发送包…...
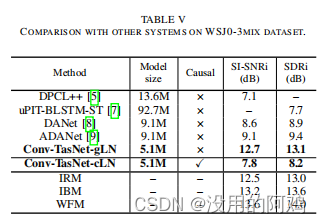
单通道说话人语音分离——Conv-TasNet(Convolutional Time-domain audio separation Network)
单通道说话人语音分离——Conv-TasNet模型(Convolutional Time-domain audio separation Network) 参考文献:《Conv-TasNet: Surpassing Ideal Time-FrequencyMagnitude Masking for Speech Separation》 1.背景 在真实的声学环境中,鲁棒的语音处理通常…...
)
华为OD机试真题Python实现【环中最长子串】真题+解题思路+代码(20222023)
环中最长子串 题目 给你一个字符串s,首尾相连成一个环形, 请你在环中找出o字符出现了偶数次最长子字符串的长度. 备注: 1 <= s.lenth <= 5x10^5 s只包含小写英文字母 🔥🔥🔥🔥🔥👉👉👉👉👉👉 华为OD机试(Python)真题目录汇总 ## 输入 输入是…...

Netcat安装与使用(nc)
Netcat安装与使用1.Netcat简介1.1.Netcat安装1.1.1.安装整体流程1.1.1.1.安装依赖1.1.1.2.安装Netcat1.1.1.3.配置环境变量1.1.1.4.测试1.2.Netcat基本功能1.3.Netcat常用参数2.Netcat用法2.1.前期准备2.2.banner相关信息抓取2.3.端口扫描2.3.1.扫描指定端口2.3.2.扫描指定端口…...
蓝桥杯:聪明的猴子
题目链接:聪明的猴子https://www.lanqiao.cn/problems/862/learning/ 目录 题目描述 输入描述 输出描述 输入输出样例 运行限制 解题思路: 最小生成树 AC代码(Java): 课后练习: 题目描述 在一个热带雨林中生存…...

Spring Boot应用如何快速接入Prometheus监控
1. Micrometer简介Micrometer为Java平台上的性能数据收集提供了一个通用的API,它提供了多种度量指标类型(Timers、Guauges、Counters等),同时支持接入不同的监控系统,例如Influxdb、Graphite、Prometheus等。可以通过M…...
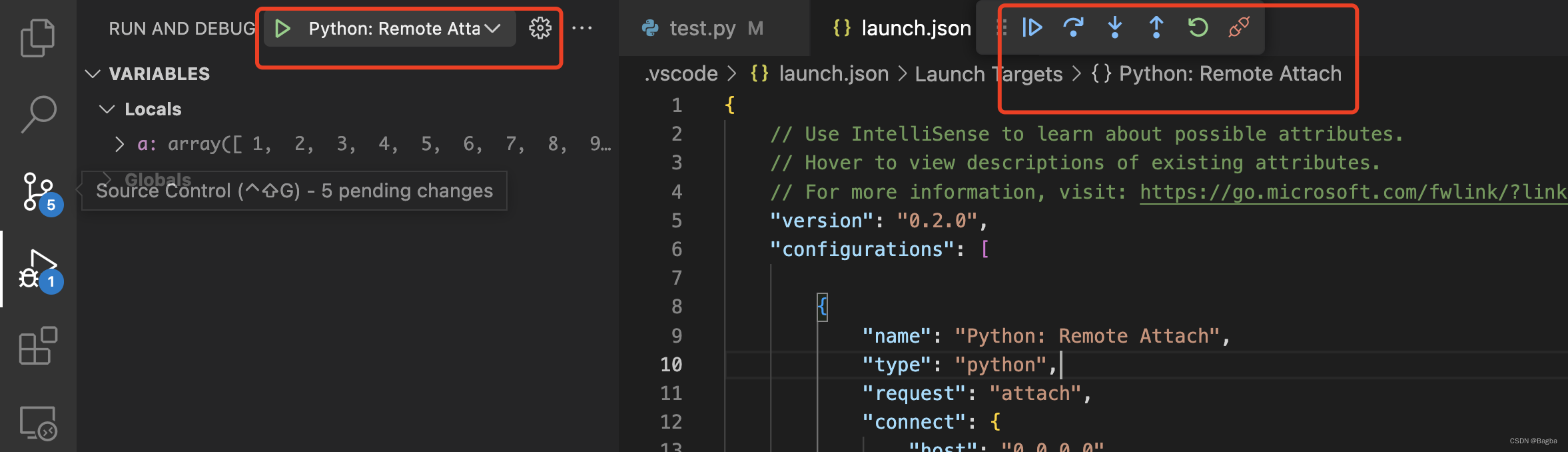
vscode远程调试python
目的 注意:这里我们想要实现的是:用vscode 使用remote ssh打开project,然后直接在project里面进行debug,而不需要 在本地vscode目录打开一样的project。 假设大家已经会使用remote ssh打开远程服务器的代码了,那么只…...
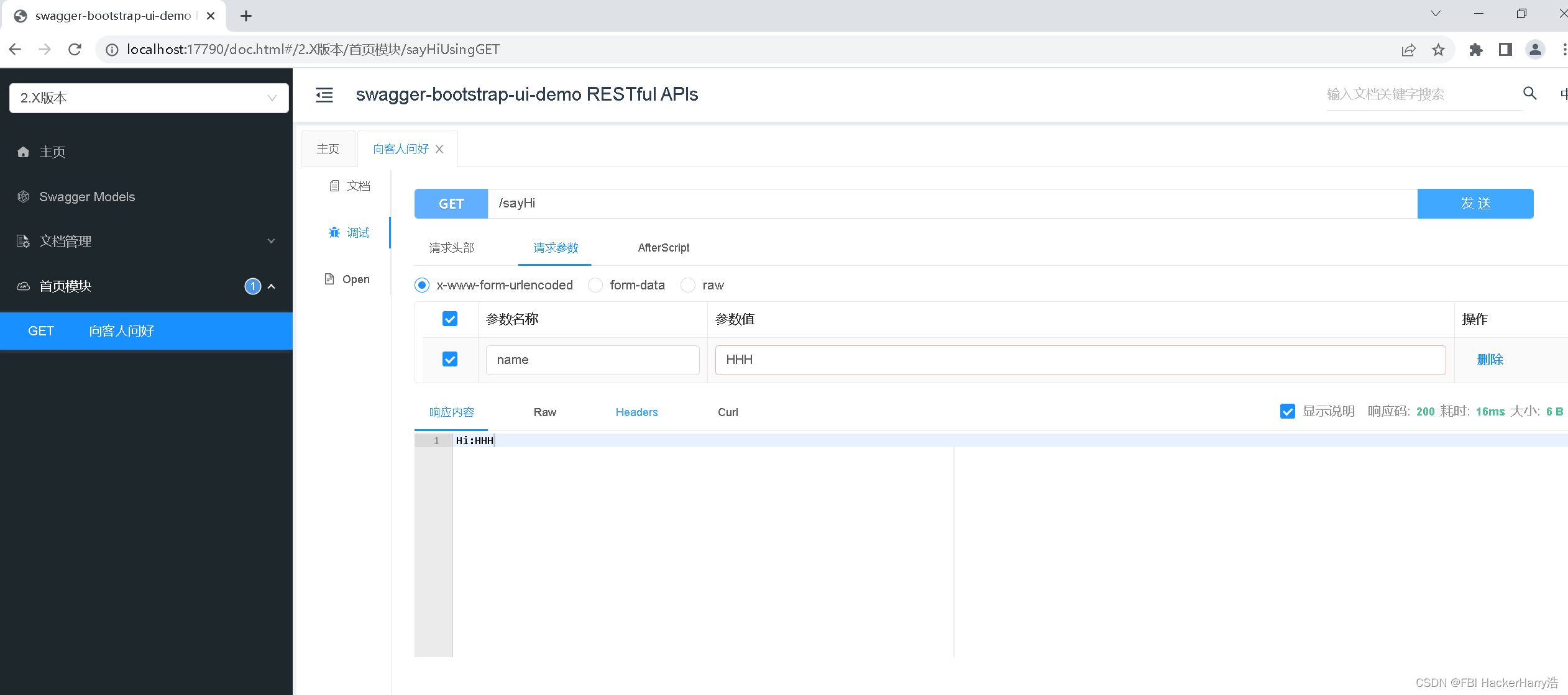
Spring Boot 框架 集成 Knife4j(内含源代码)
Spring Boot 框架 集成 Knife4j(内含源代码) 源代码下载链接地址:https://download.csdn.net/download/weixin_46411355/87480176 目录Spring Boot 框架 集成 Knife4j(内含源代码)源代码下载链接地址:[htt…...

什么蓝牙耳机适合打游戏?打游戏不延迟的蓝牙耳机
为了提升游戏体验,除了配置强悍的主机外,与之搭配蓝牙耳机等外设产品也尤为重要,今天就带大家来了解一下以下几款适合玩游戏,低延迟操作的蓝牙耳机。 第一款:南卡小音舱蓝牙耳机 参考价格:239元 推荐理由…...
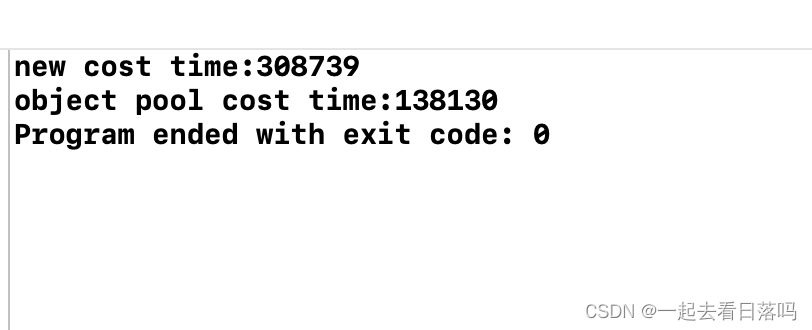
【项目设计】高并发内存池(一)[项目介绍|内存池介绍|定长内存池的实现]
🎇C学习历程:入门 博客主页:一起去看日落吗持续分享博主的C学习历程博主的能力有限,出现错误希望大家不吝赐教分享给大家一句我很喜欢的话: 也许你现在做的事情,暂时看不到成果,但不要忘记&…...
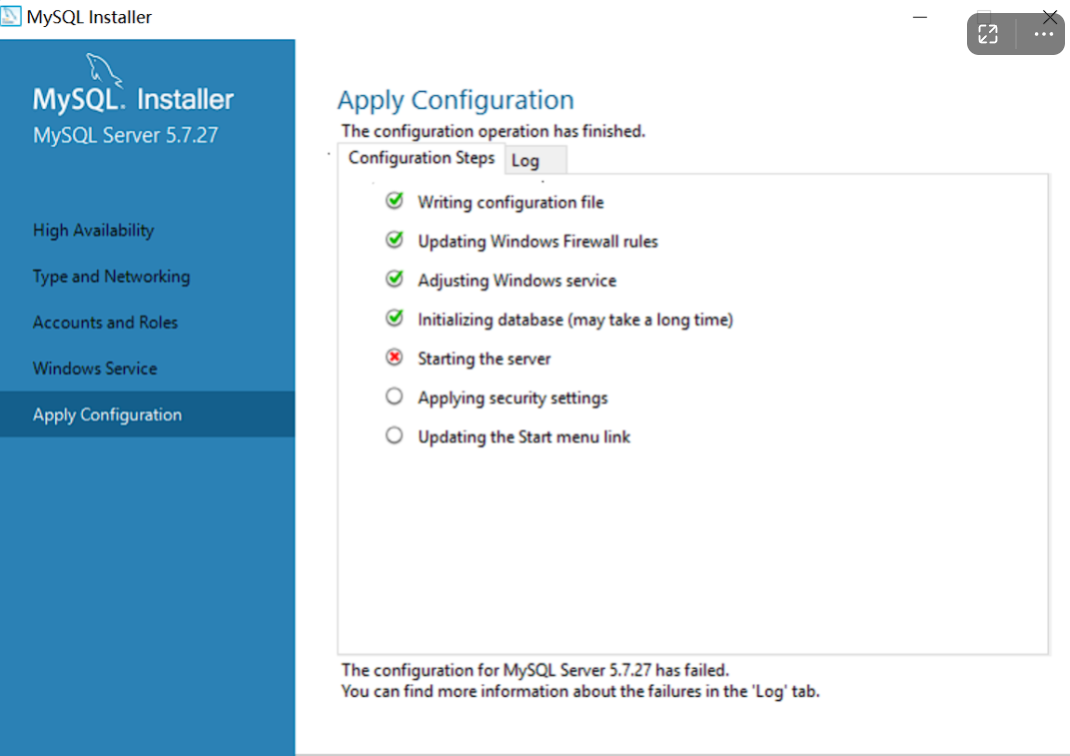
初识MySQL下载与安装【快速掌握知识点】
目录 前言 MySQL版本 MySQL类型 MySQL官网有.zip和.msi两种安装形式; MySQL 下载 1、MySQL 属于 Oracle 旗下产品,进入Oracle官网下载 2、点击产品,找到MySQL 3、进入MySQL页面 4、点击Download(下载)&#x…...
如何终止一个线程
如何终止一个线程 是使用 thread.stop() 吗? public class ThreadDemo extends Thread{Overridepublic void run() {try {Thread.sleep(10000);} catch (InterruptedException e) {e.printStackTrace();}System.out.println("this is demo thread :"Thre…...

上岸!选择你的隐私计算导师!
开放隐私计算 开放隐私计算开放隐私计算OpenMPC是国内第一个且影响力最大的隐私计算开放社区。社区秉承开放共享的精神,专注于隐私计算行业的研究与布道。社区致力于隐私计算技术的传播,愿成为中国 “隐私计算最后一公里的服务区”。183篇原创内容公众号…...
go gin学习记录5
有了前面几节的学习,如果做个简单的web服务端已经可以完成了。 这节来做一下优化。 我们实验了3种SQL写入的方法,但是发现每一种都需要在方法中去做数据库链接的操作,有些重复了。 所以,我们把这部分提取出来,数据库链…...
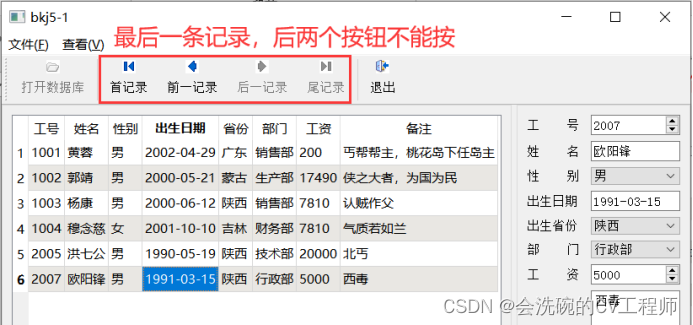
PyQt5数据库开发2 5.1 QSqlQueryModel
目录 一、Qt窗体设计 1. 新建Qt项目 2. 拷贝4-3的部分组件过来 3. 添加资源文件 4. 创建Action 5. 添加工具栏 6. 创建菜单项 7. 关闭Action的实现 8. 调整布局 8.1 调整两个groupbox的布局 8.3 为窗体设置全局布局 二、代码拷贝和删除 1. 新建项目目录 2. 编译…...

MySQL-redo log和undo log
什么是事务 事务是由数据库中一系列的访问和更新组成的逻辑执行单元 事务的逻辑单元中可以是一条SQL语句,也可以是一段SQL逻辑,这段逻辑要么全部执行成功,要么全部执行失败 举个最常见的例子,你早上出去买早餐,支付…...
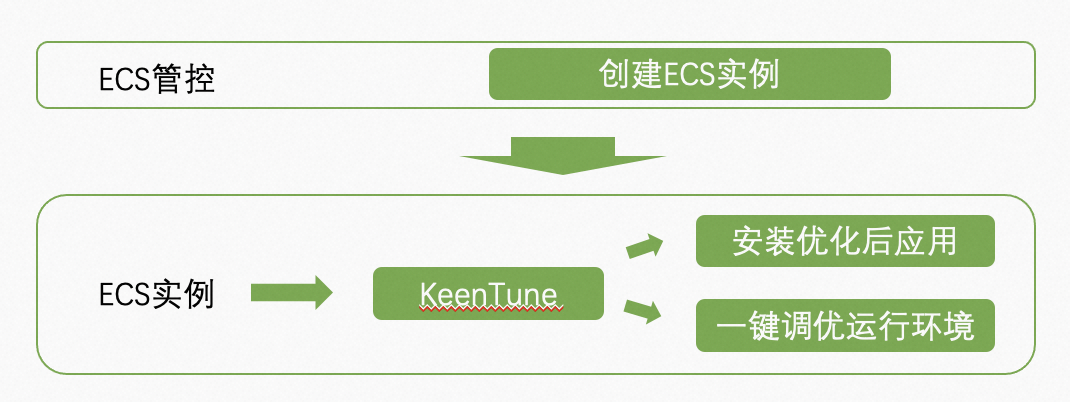
阿里云ECS TOP性能提升超20%!KeenTune助力倚天+Alinux3达成开机即用的全栈性能调优 | 龙蜥技术
文/KeenTune SIG01阿里云 ECS 上售卖页新增“应用加速”功能2023年1月12日 阿里云 ECS 的售卖页有了一些新的变化,在用户选择倚天 Alinux3 新建实例时,多了一个新的选项“应用加速”。这个功能是 阿里云 ECS 基于 KeenTune 提供典型云场景的开机即用的全…...
)
华为OD机试真题Python实现【快递业务站】真题+解题思路+代码(20222023)
快递业务站 题目 快递业务范围有 N 个站点,A 站点与 B 站点可以中转快递,则认为 A-B 站可达, 如果 A-B 可达,B-C 可达,则 A-C 可达。 现在给 N 个站点编号 0、1、…n-1,用 s[i][j]表示 i-j 是否可达, s[i][j] = 1表示 i-j可达,s[i][j] = 0表示 i-j 不可达。 现用二维…...

【c语言】预处理
🚀write in front🚀 📜所属专栏:> c语言学习 🛰️博客主页:睿睿的博客主页 🛰️代码仓库:🎉VS2022_C语言仓库 🎡您的点赞、关注、收藏、评论,是…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

人工智能--安全大模型训练计划:基于Fine-tuning + LLM Agent
安全大模型训练计划:基于Fine-tuning LLM Agent 1. 构建高质量安全数据集 目标:为安全大模型创建高质量、去偏、符合伦理的训练数据集,涵盖安全相关任务(如有害内容检测、隐私保护、道德推理等)。 1.1 数据收集 描…...

LOOI机器人的技术实现解析:从手势识别到边缘检测
LOOI机器人作为一款创新的AI硬件产品,通过将智能手机转变为具有情感交互能力的桌面机器人,展示了前沿AI技术与传统硬件设计的完美结合。作为AI与玩具领域的专家,我将全面解析LOOI的技术实现架构,特别是其手势识别、物体识别和环境…...

学习一下用鸿蒙DevEco Studio HarmonyOS5实现百度地图
在鸿蒙(HarmonyOS5)中集成百度地图,可以通过以下步骤和技术方案实现。结合鸿蒙的分布式能力和百度地图的API,可以构建跨设备的定位、导航和地图展示功能。 1. 鸿蒙环境准备 开发工具:下载安装 De…...
