求二维子数组的和(剖析)
文章目录
- 🐒个人主页
- 🏅JavaSE系列专栏
- 📖前言:本篇剖析一下二维子数组求和
- 规则:
🐒个人主页
🏅JavaSE系列专栏
📖前言:本篇剖析一下二维子数组求和
规则:
这是一个4 X 4的二维数组a[][]
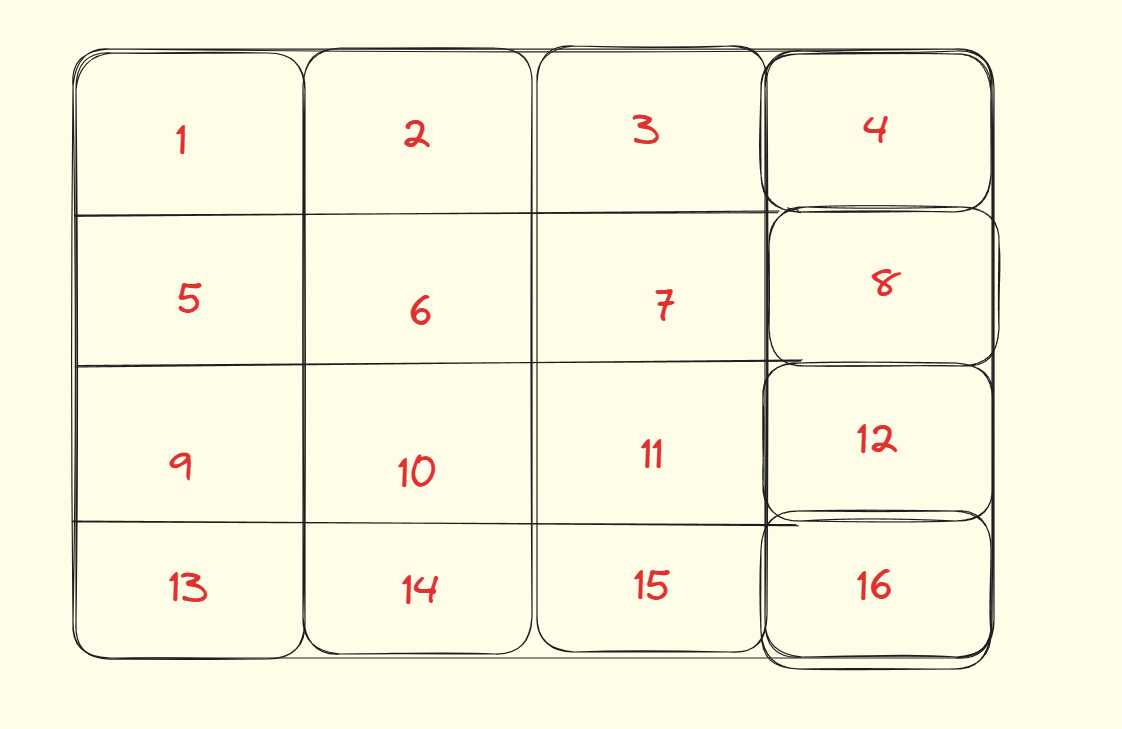
假设再来一个4 X 4的空数组,
第一个位置是a[0][0],(前一个元素的和)
第二个位置是a[0][0]+a[0][1]+a[0][2],(前两个元素的和)
第三个位置是a[0][0]+a[0][1]+a[0][2],(前三个元素的和)
第四个位置是a[0][0]+a[0][1]+a[0][2]+a[0][3],
第五个位置是a[0][0]+a[1][0],
…
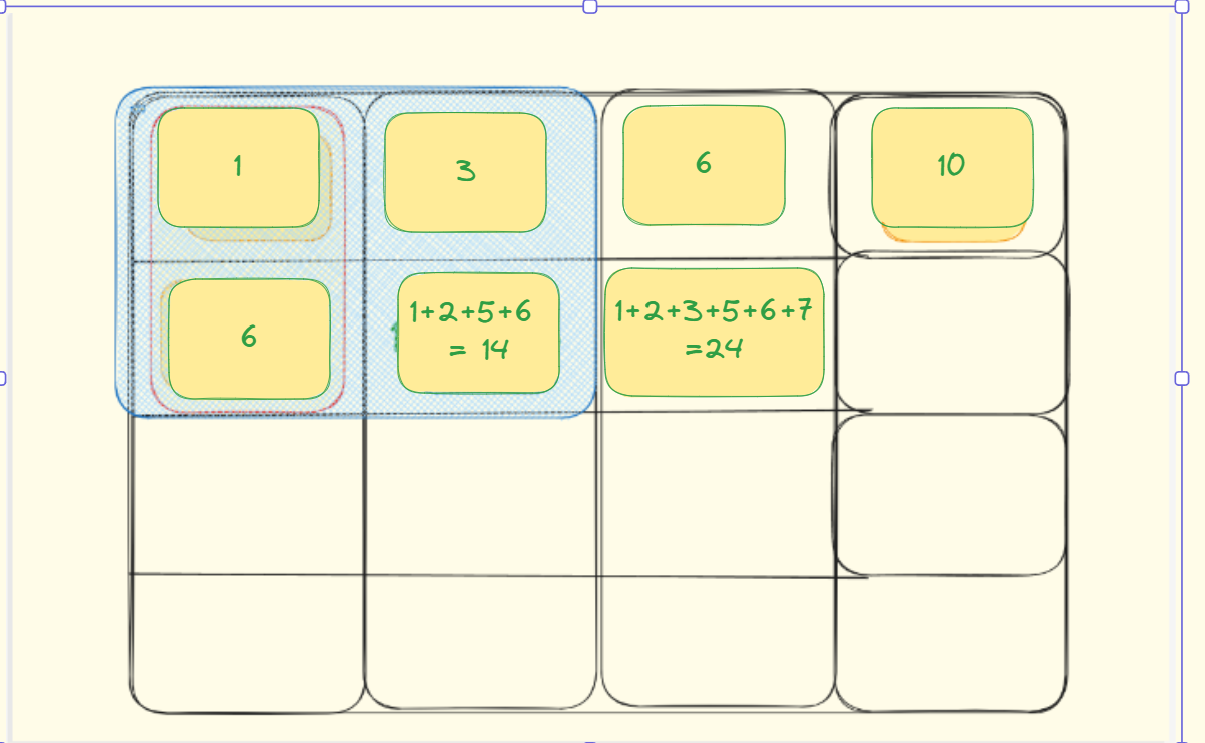
那么用java程序应该如何实现呢:
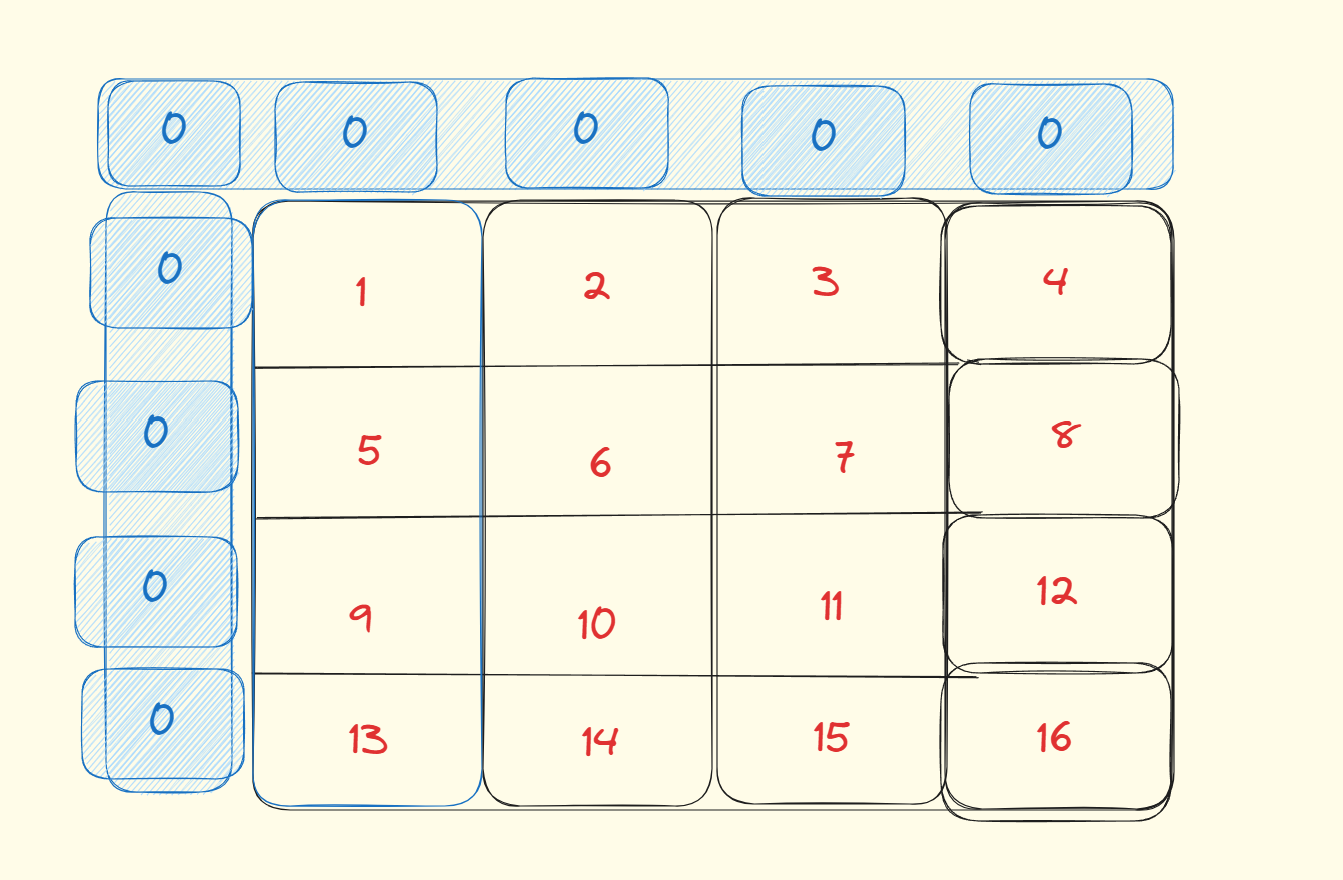
比如说:求值为7这个位置的和:1+2+3+5+6+7
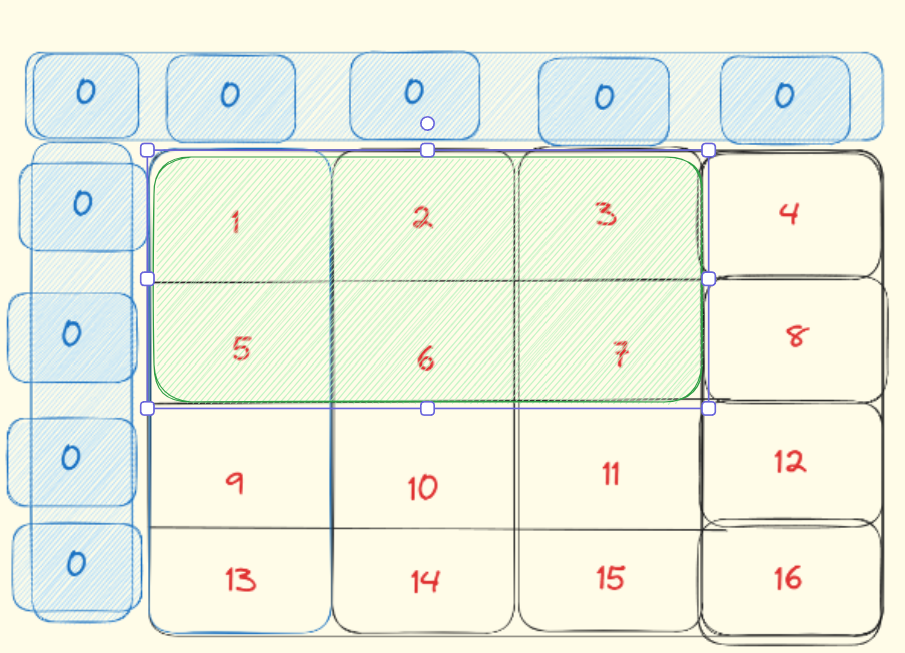
可以分解为:三个红色的-一个重复的绿色
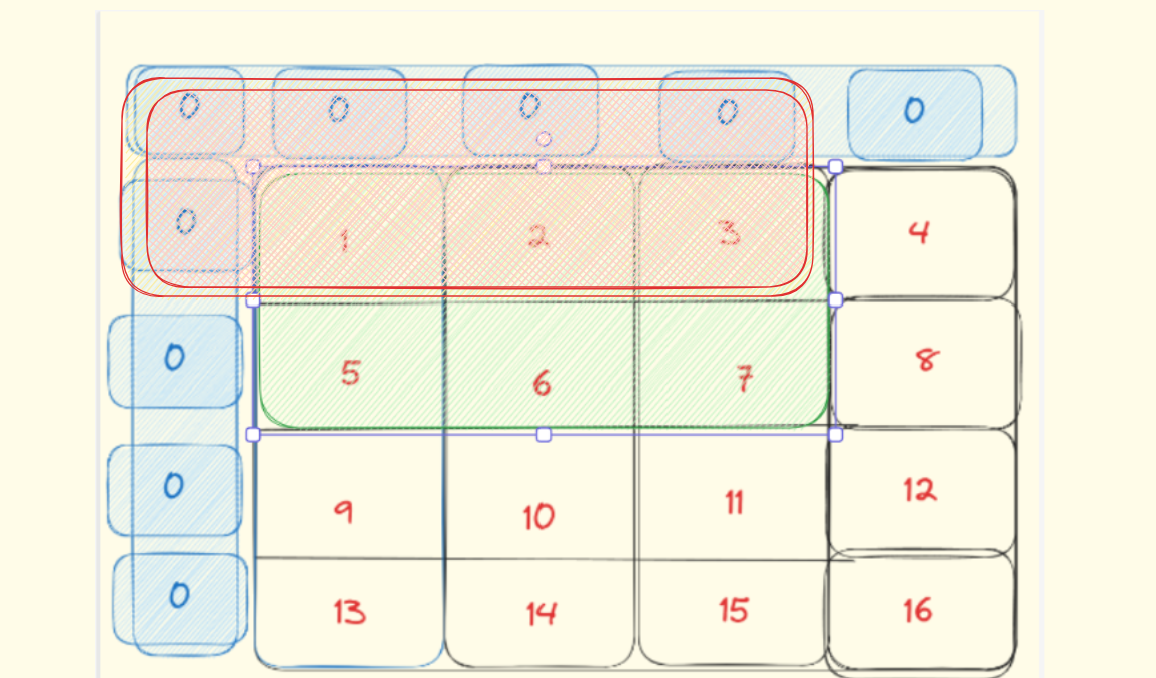
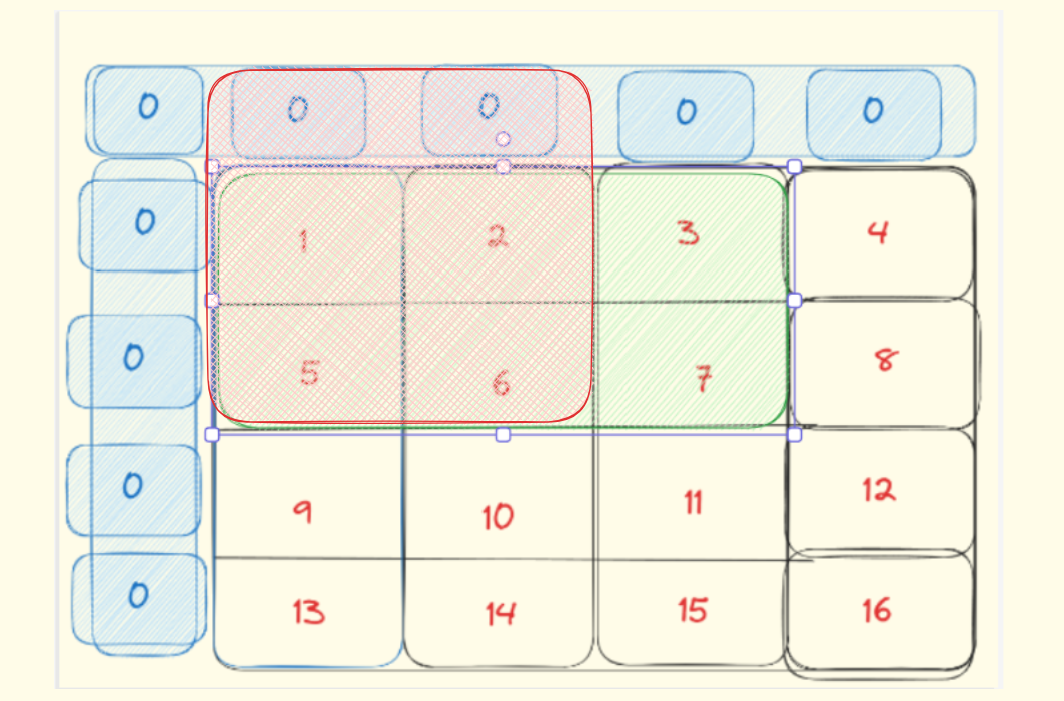
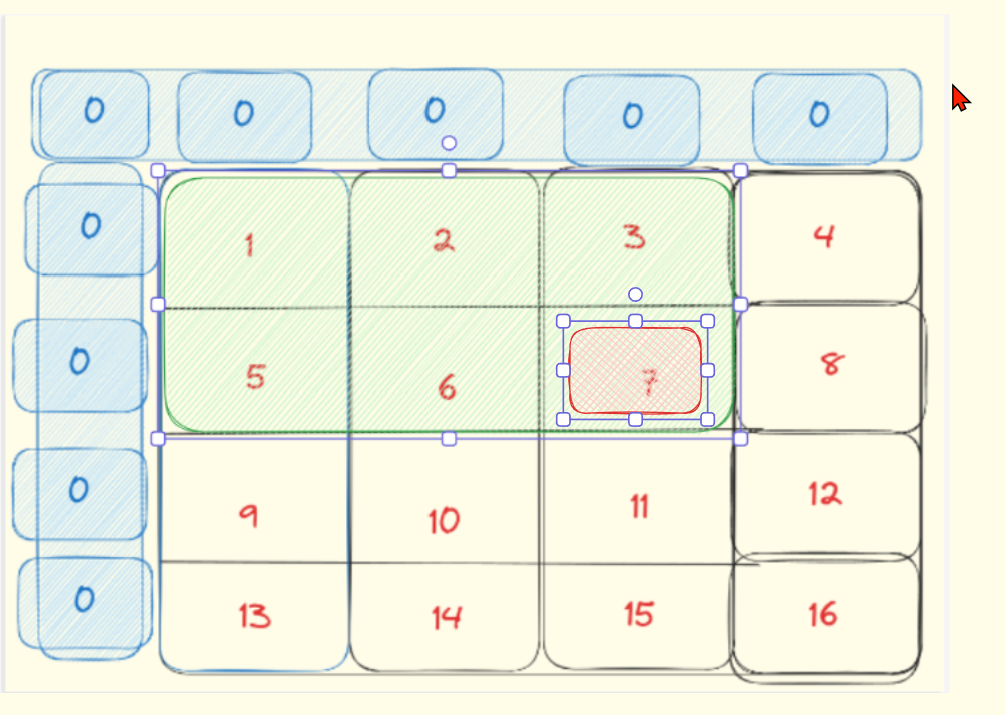
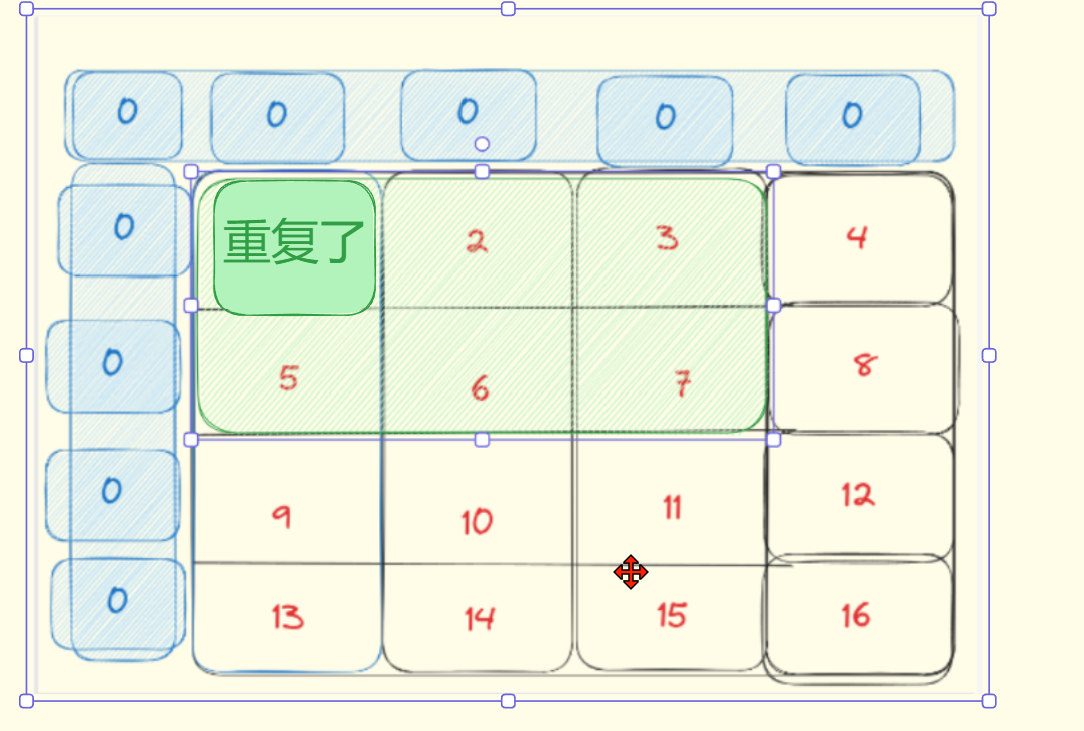
即: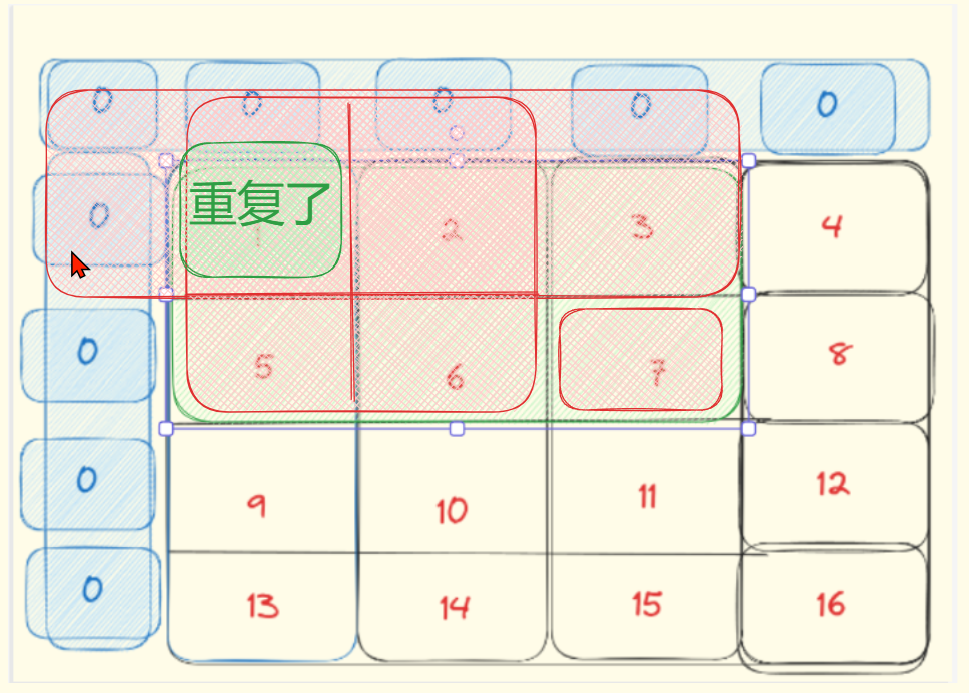
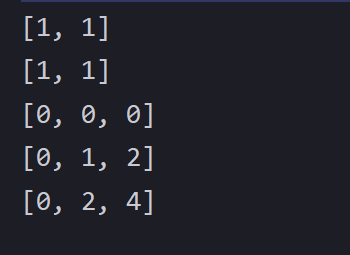
//初始化数组int [][] a=new int[2][2];for (int i = 0; i <a.length ; i++) {for (int j = 0; j <a[i].length ; j++) {a[i][j]=1;}System.out.println(Arrays.toString(a[i]));}//存储求和的数组int[][] sum=new int[a.length+1][a[0].length+1];//这里需要额外加一行+加一列for (int i = 1; i <sum.length ; i++) {for (int j = 1; j <sum.length ; j++) {//核心语句:sum[i][j]=sum[i][j-1]+sum[i-1][j]-sum[i-1][j-1]+a[i-1][j-1];//行成立的+列成立的-重合的+新增的}}//打印出结果for (int i = 0; i <sum.length ; i++) {System.out.println(Arrays.toString(sum[i]));}
相关文章:

求二维子数组的和(剖析)
文章目录 🐒个人主页🏅JavaSE系列专栏📖前言:本篇剖析一下二维子数组求和规则: 🐒个人主页 🏅JavaSE系列专栏 📖前言:本篇剖析一下二维子数组求和 规则: 这…...
代码开发思路介绍)
无(低)代码开发思路介绍
无代码或者低代码开发的思路,是通过非编程代码,而是基于页面拖拉拽的方式来实现创建web应用的功能。 作为程序员我们知道私有云公有云已经实现了基础设施的web方式管理。DEVOPS把代码发布,管理也实现了web方式管理。那么我们很容易能够想到,只要把拖拉拽出来的项目自动化部…...

代码随想录刷题 Day14
144.二叉树的前序遍历(opens new window) 要注意下创建函数参数传递不是很理解 class Solution { public:void tranversal(TreeNode* s, vector<int> &b) {if (s NULL) {return;}b.push_back(s->val);tranversal(s->left, b);tranversal(s->right, b);}v…...

二分类问题的解决利器:逻辑回归算法详解(一)
文章目录 🍋引言🍋逻辑回归的原理🍋逻辑回归的应用场景🍋逻辑回归的实现 🍋引言 逻辑回归是机器学习领域中一种重要的分类算法,它常用于解决二分类问题。无论是垃圾邮件过滤、疾病诊断还是客户流失预测&…...

docker alpine镜像中遇到 not found
1.问题: docker alpine镜像中遇到 sh: xxx: not found 例如 # monerod //注:此可执行文件已放到/usr/local/bin/ sh: monerod: not found2.原因 由于alpine镜像使用的是musl libc而不是gnu libc,/lib64/ 是不存在的。但他们是兼容的&…...

python的多线程多进程与多协程
python的多线程是假多线程,本质是交叉串行,并不是严格意义上的并行,或者可以这样说,不管怎么来python的多线程在同一时间有且只有一个线程在执行(举个例子,n个人抢一个座位,但是座位就这一个,不…...

一文介绍使用 JIT 认证后实时同步用户更加优雅
首先本次说的 JIT 指的是 Just In Time ,可以理解为及时录入,一般用在什么样的场景呢? 还记的上次我们说过关于第三方组织结构同步的功能实现,主要目的是将第三方源数据同步到内部平台中来,方便做管控和处理 此处的管…...

搞定“项目八怪”,你就是管理高手!
大家好,我是老原。 玛丽.弗列特说:“权力已经逐渐被视为一个群体的组合能力。我们通过有效联系获取力量。” 有效联系也就是指的沟通,这个部分占据我们项目经理工作内容的80%,可见沟通在项目管理中的重要性。 项目经理的沟通包…...
机器视觉-标定篇
3D结构光标定 结构光视觉的优点: 非接触、信息量大、测精度高、抗干扰能力强。 结构光视觉传感器参数的标定包括:摄像机参数标定、结构光平面参数标定。 结构光视觉测量原理图 我们不考虑镜头的畸变,将相机的成像模型简化为小孔成像模型…...

linux离线安装make
一、下载rpm包 https://pkgs.org/search/?qmake 二、拷贝至服务器 三、安装make rpm -ivh make-3.82-24.el7.x86_64.rpm四、查看是否安装成功 make -v...

【深度学习】卷积神经网络(LeNet)【文章重新修改中】
卷积神经网络 LeNet 前言LeNet 模型代码实现MINST代码分块解析1 构建 LeNet 网络结构2 加载数据集3 初始化模型和优化器4 训练模型5 训练完成 完整代码 Fashion-MINST代码分块解析1 构建 LeNet 网络结构2 初始化模型参数3 加载数据集4 定义损失函数和优化器5 训练模型 完整代码…...
win10 Baichuan2-7B-Chat-4bits 上部署 百川2-7B-对话模型-4bits量化版
搞了两天才搞清楚跑通 好难呢,个人电脑 win10 ,6GB显存 个人感觉 生成速度很慢,数学能力不怎么行 没有ChatGLM2-6B 强,逻辑还行, 要求: 我的部署流程 1.下载模型 ,下载所有文件 然后 放到新建的model目录 https://huggingface.co/baichuan-inc/Baichuan2-7B-Chat-4bits/tr…...
2023/9/20总结
maven maven本质是 一个项目管理工具 将项目开发 和 管理过程 抽象成 一个项目对象模型(POM) POM (Project Object Model) 项目对象模型 作用 项目构建 提供标准的自动化 项目构建 方式依赖管理 方便快捷的管理项目依赖的资源…...

【Git】git 分支或指定文件回退到指定版本
目录 一、分支回滚 1. 使用 git reset 命令 2.使用 git revert 命令 3.使用 git checkout 命令 二、某个文件回滚 1.查看哪些文件发生修改 2.然后查看提交记录(最近几次提交) 3.执行提交命令 一、分支回滚 1. 使用 git reset 命令 命令可以将当前分支的 HEAD 指针指向指…...
Java 消息策略的实现 - Kafak 是怎么设计的
这个也是开放讨论题,主要讨论下 Kafka 在消息中是如何进行实现的。 1_cCyPNzf95ygMFUgsrleHtw976506 21.4 KB 总结 这个题目的开发性太强了。 Kafka 可以用的地方非常多,我经历过的项目有 Kafka 用在消息处理策略上的。这个主要是 IoT 项目,…...
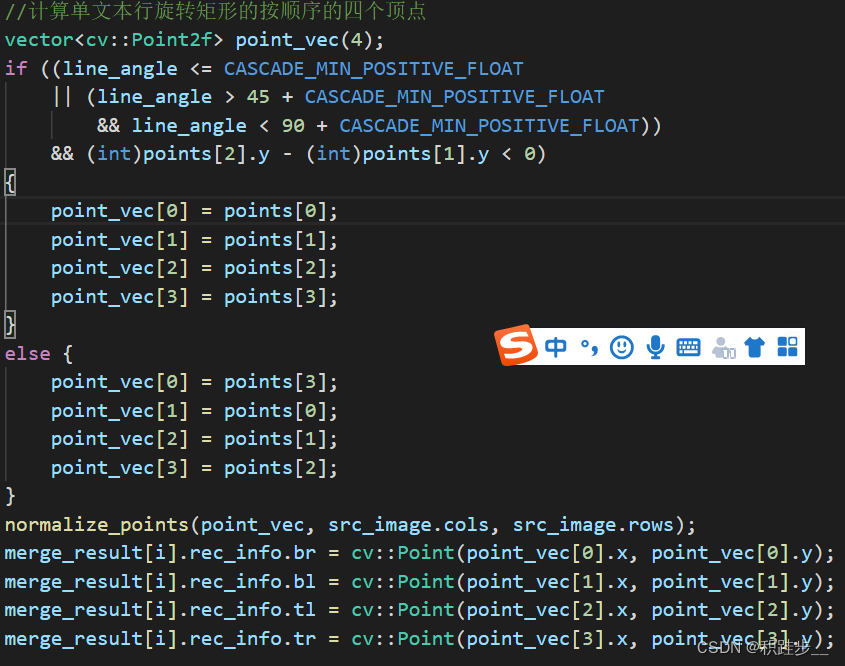
c++opencv RotatedRect 旋转矩形角度转换和顶点顺序转换
这里写自定义目录标题 以下代码记录主要是完成轮廓点求解最小外接矩形之后计算该文本行的角度和旋转矩形的左下(bl),左上(tl),右上(tr),右下(br)的坐标点。 RotatedRect rtminAreaRect(contours…...
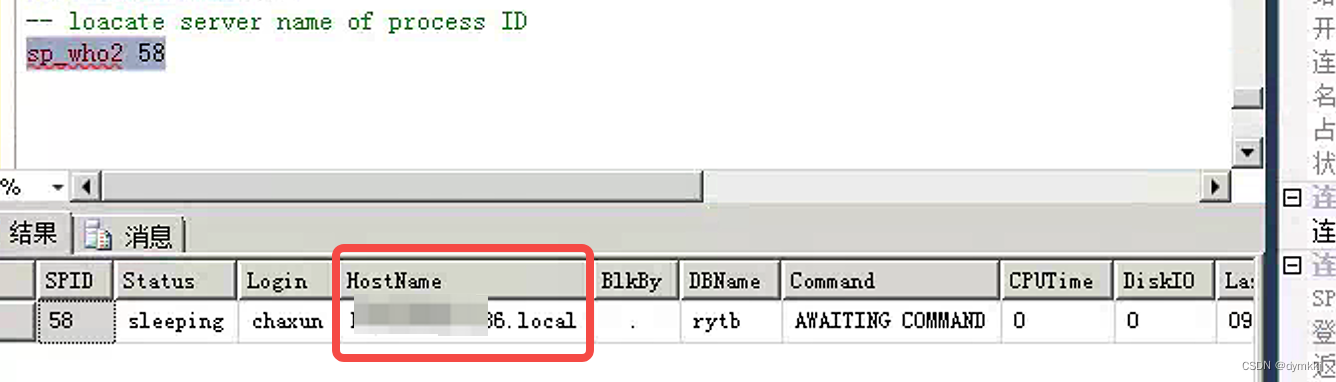
Flink-CDC 抽取SQLServer问题总结
Flink-CDC 抽取SQLServer问题总结 背景 flink-cdc 抽取数据到kafka 中,使用flink-sql进行开发,相关问题总结flink-cdc 配置SQLServer cdc参数 1.创建CDC 使用的角色, 并授权给其查询待采集数据数据库 -- a.创建角色 create role flink_role;-- b.授权…...
Linux 系统目录结构 终端
系统目录结构 Linux 或 Unix 操作系统中,所有文件和目录呈一个以根节点为始的倒置的树状结构。文件系统的最顶层是根目录,用 / 来表示根目录。在根目录之下的既可以是目录,也可以是文件,而每一个目录中又可以包含子目录文件。如此…...

Layui + Flask | 实现注册、登录功能(案例篇)(08)
此案例内容比较多,建议滑到最后点击阅读原文,阅读体验更佳。后续也会录制案例视频,将在本周内上传到同名的 b 站账号。 已经看了 layui 表单相关的知识,接下来就可以实现注册功能,功能逻辑如下: 项目创建 新建 flask 项目下载 layui 文件,解压之后复制到指定文件编写前…...

GitLab数据迁移后出现500错误
一、背景 去年做GitLab数据迁移时,写过一篇文章《GitLab的备份与还原》。后来发现新创建的项目没问题,但对于迁移过来的项目,修改名称等信息,或者删除该项目时,会出现500错误,以为是系统问题&#…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...

【JavaSE】多线程基础学习笔记
多线程基础 -线程相关概念 程序(Program) 是为完成特定任务、用某种语言编写的一组指令的集合简单的说:就是我们写的代码 进程 进程是指运行中的程序,比如我们使用QQ,就启动了一个进程,操作系统就会为该进程分配内存…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...
