【动态规划刷题 16】最长等差数列 (有难度) 等差数列划分 II - 子序列
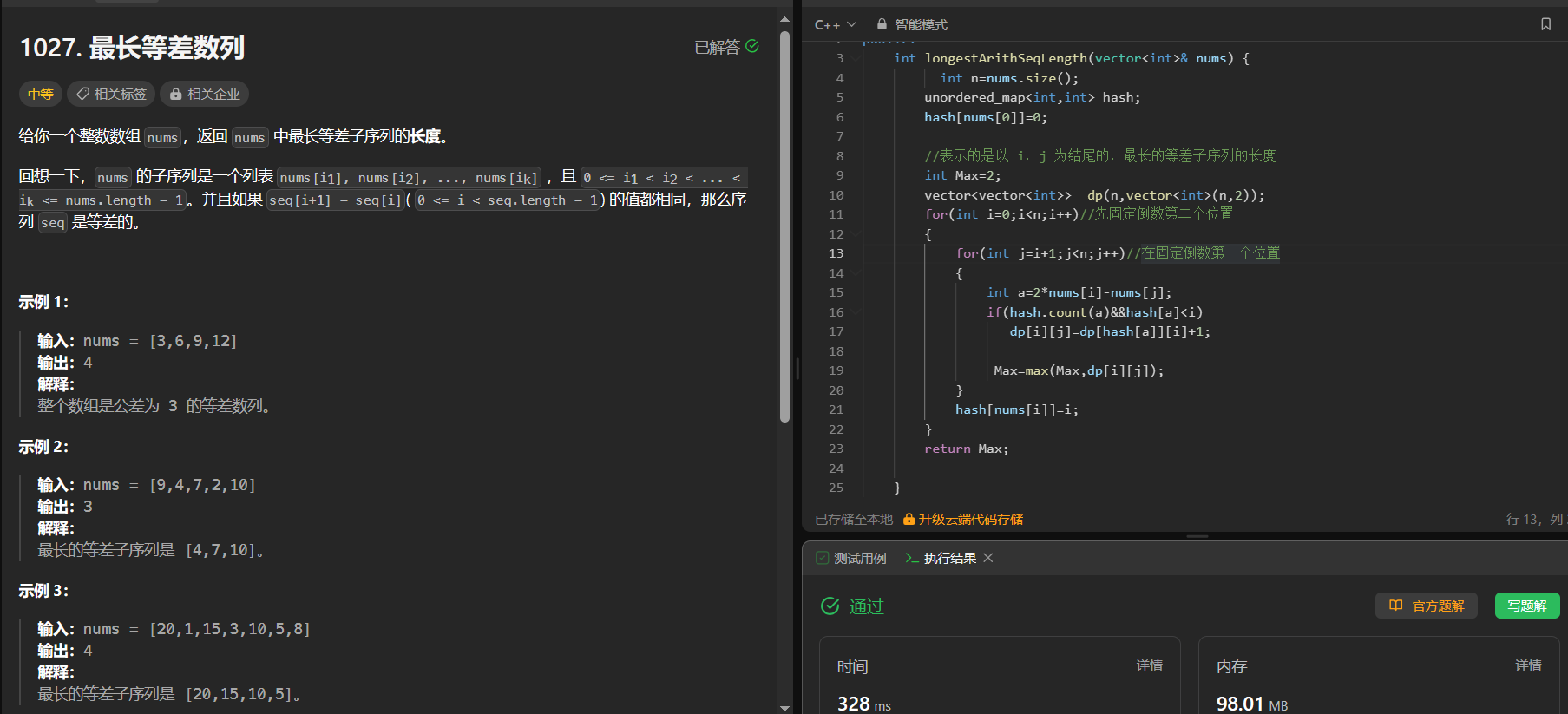
1027. 最长等差数列
https://leetcode.cn/problems/longest-arithmetic-subsequence/
给你一个整数数组 nums,返回 nums 中最长等差子序列的长度。
回想一下,nums 的子序列是一个列表 nums[i1], nums[i2], …, nums[ik] ,且 0 <= i1 < i2 < … < ik <= nums.length - 1。并且如果 seq[i+1] - seq[i]( 0 <= i < seq.length - 1) 的值都相同,那么序列 seq 是等差的。
示例 1:
输入:nums = [3,6,9,12]
输出:4
解释:
整个数组是公差为 3 的等差数列。
示例 2:
输入:nums = [9,4,7,2,10]
输出:3
解释:
最长的等差子序列是 [4,7,10]。
示例 3:
输入:nums = [20,1,15,3,10,5,8]
输出:4
解释:
最长的等差子序列是 [20,15,10,5]。
1.状态表示*
我们先试着定义一个状态转移数组:
dp[i] 表⽰:以 i 位置元素为结尾的「所有⼦序列」中,最⻓的等差序列的⻓度。
但是这⾥有⼀个⾮常致命的问题,那就是我们⽆法确定 i 结尾的等差序列的样⼦。这样就会导致我们⽆法推导状态转移⽅程,因此我们定义的状态表⽰需要能够确定⼀个等差序列:
dp[i][j] 表⽰:以 i 位置以及 j 位置的元素为结尾的所有的⼦序列中,最⻓的等差序列的⻓度。
2.状态转移方程
设 nums[i] = b, nums[j] = c ,那么这个序列的前⼀个元素就是 a = 2 * b - c 。我们
根据 a 的情况讨论:
- a 存在,下标为 k ,并且 a < b :此时我们需要以 k 位置以及 i 位置元素为结尾的最⻓等差序列的⻓度,然后再加上 j 位置的元素即可。于是
dp[i][j] = dp[k][i] +1。这⾥因为会有许多个 k ,我们仅需离 i 最近的 k 即可。因此任何最⻓的都可以以 k 为结尾; - a 存在,但是 b < a < c :此时只能两个元素⾃⼰玩了, dp[i][j] = 2 ;
- a 不存在:此时依旧只能两个元素⾃⼰玩了, dp[i][j] = 2 ;
优化:
⼀边 dp ,⼀边保存。这种⽅式,我们仅需保存最近的元素的下标,不⽤保存下标数组。但是⽤这种⽅法的话,我们在遍历顺序那⾥,先固定倒数第⼆个数,再遍历倒数第⼀个数。这样就可以在 i 使⽤完时候,将 nums[i] 扔到哈希表中。
3. 初始化
根据实际情况,可以将所有位置初始化为 2 。
4. 填表顺序
a. 先固定倒数第⼆个数;
b. 然后枚举倒数第⼀个数。
5. 返回值
由于不知道最⻓的结尾在哪⾥,因此返回 dp 表中的最⼤值。
代码:
int longestArithSeqLength(vector<int>& nums) {int n=nums.size();unordered_map<int,int> hash;hash[nums[0]]=0;//表示的是以 i,j 为结尾的,最长的等差子序列的长度int Max=2;vector<vector<int>> dp(n,vector<int>(n,2));for(int i=0;i<n;i++)//先固定倒数第二个位置{for(int j=i+1;j<n;j++)//在固定倒数第一个位置{int a=2*nums[i]-nums[j];if(hash.count(a)&&hash[a]<i)dp[i][j]=dp[hash[a]][i]+1;Max=max(Max,dp[i][j]);}hash[nums[i]]=i;}return Max;}
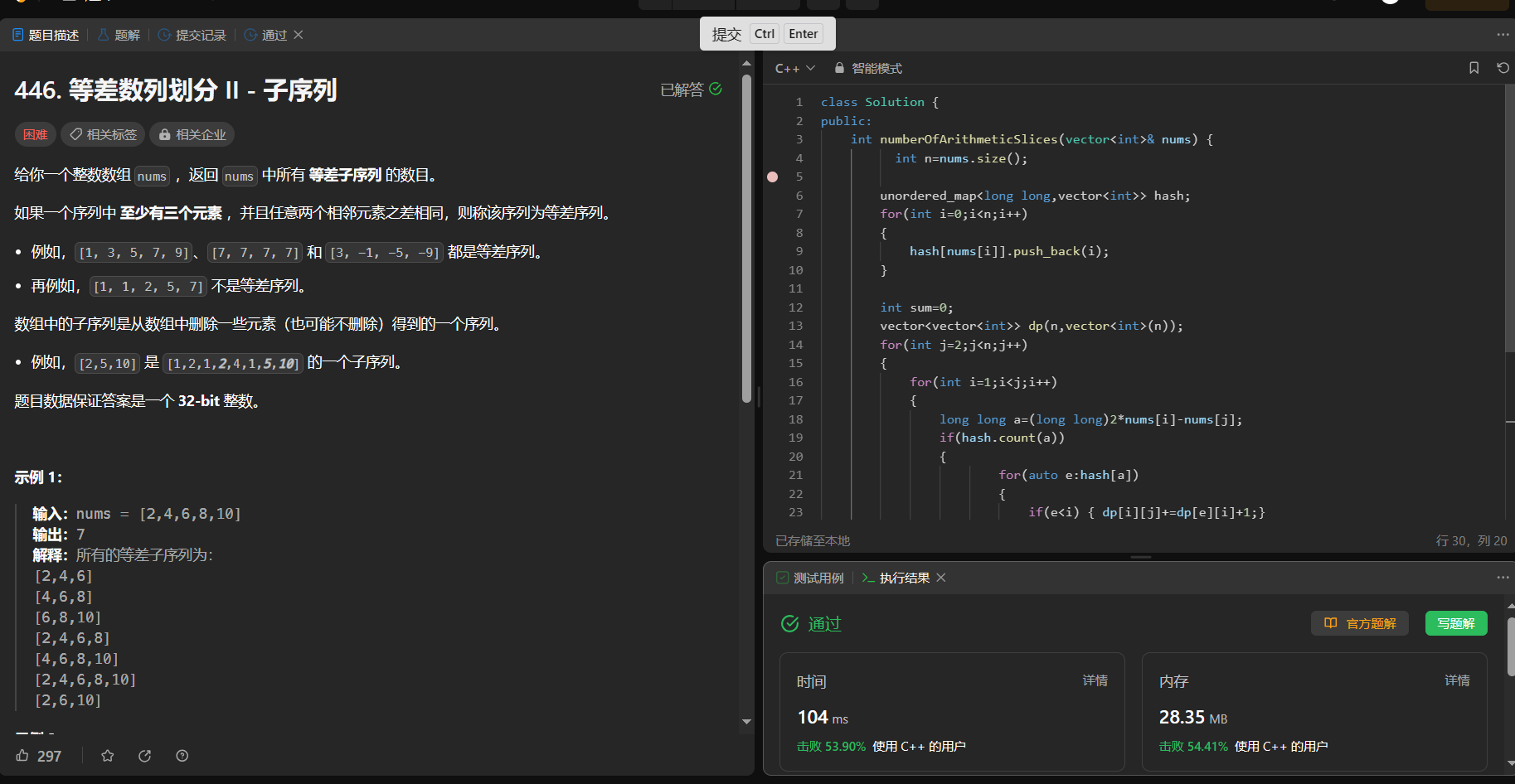
446. 等差数列划分 II - 子序列
https://leetcode.cn/problems/arithmetic-slices-ii-subsequence/
给你一个整数数组 nums ,返回 nums 中所有 等差子序列 的数目。
如果一个序列中 至少有三个元素 ,并且任意两个相邻元素之差相同,则称该序列为等差序列。
例如,[1, 3, 5, 7, 9]、[7, 7, 7, 7] 和 [3, -1, -5, -9] 都是等差序列。
再例如,[1, 1, 2, 5, 7] 不是等差序列。
数组中的子序列是从数组中删除一些元素(也可能不删除)得到的一个序列。
例如,[2,5,10] 是 [1,2,1,2,4,1,5,10] 的一个子序列。
题目数据保证答案是一个 32-bit 整数。
示例 1:
输入:nums = [2,4,6,8,10]
输出:7
解释:所有的等差子序列为:
[2,4,6]
[4,6,8]
[6,8,10]
[2,4,6,8]
[4,6,8,10]
[2,4,6,8,10]
[2,6,10]
示例 2:
输入:nums = [7,7,7,7,7]
输出:16
解释:数组中的任意子序列都是等差子序列。
1.状态表示*
我们先试着定义一个状态转移数组:
dp[i] 表⽰:以 i 位置元素为结尾的「所有⼦序列」中,最⻓的等差序列的⻓度。
但是这⾥有⼀个⾮常致命的问题,那就是我们⽆法确定 i 结尾的等差序列的样⼦。这样就会导致我们⽆法推导状态转移⽅程,因此我们定义的状态表⽰需要能够确定⼀个等差序列:
dp[i][j] 表⽰:以 i 位置以及 j 位置的元素为结尾的所有的⼦序列中,等差⼦序列的个数。
2.状态转移方程
设 nums[i] = b, nums[j] = c ,那么这个序列的前⼀个元素就是 a = 2 * b - c 。我们
根据 a 的情况讨论:
- a 存在,下标为 k ,并且 a < b :此时我们需要以 k 位置以及 i 位置元素为结尾的最⻓等差序列的⻓度,然后再加上 j 位置的元素即可。于是
dp[i][j] = dp[k][i] +1。这⾥因为会有许多个 k ,我们仅需离 i 最近的 k 即可。因此任何最⻓的都可以以 k 为结尾; - b. 因为 a 可能有很多个,我们需要全部累加起来
综上, dp[i][j] += dp[k][i] + 1 。
优化:
优化点:我们发现,在状态转移⽅程中,我们需要确定 a 元素的下标。因此我们可以在 dp 之前,将
所有元素 +下标数组绑定在⼀起,放到哈希表中。这⾥为何要保存下标数组,是因为我们要统计个
数,所有的下标都需要统计。
3. 初始化
刚开始是没有等差数列的,因此初始化 dp 表为 0
4. 填表顺序
a. 先固定倒数第⼆个数;
b. 然后枚举倒数第⼀个数。
5. 返回值
我们要统计所有的等差⼦序列,因此返回 dp 表中所有元素的和。
代码:
int numberOfArithmeticSlices(vector<int>& nums) {int n=nums.size();unordered_map<long long,vector<int>> hash;for(int i=0;i<n;i++){hash[nums[i]].push_back(i);}int sum=0;vector<vector<int>> dp(n,vector<int>(n));for(int j=2;j<n;j++){for(int i=1;i<j;i++){long long a=(long long)2*nums[i]-nums[j];if(hash.count(a)){for(auto e:hash[a]){if(e<i) { dp[i][j]+=dp[e][i]+1;}else break;}}sum+=dp[i][j];}}return sum;}
相关文章:

【动态规划刷题 16】最长等差数列 (有难度) 等差数列划分 II - 子序列
1027. 最长等差数列 https://leetcode.cn/problems/longest-arithmetic-subsequence/ 给你一个整数数组 nums,返回 nums 中最长等差子序列的长度。 回想一下,nums 的子序列是一个列表 nums[i1], nums[i2], …, nums[ik] ,且 0 < i1 <…...
【postgresql】替换 mysql 中的ifnull()
数据库由mysql 迁移到postgresql,程序在执行查询时候报错。 HINT: No function matches the given name and argument types. You might need to add explicit type casts. CONTEXT: referenced column: ifnull 具体SQL: SELECT ifnull(phone,) FROM c_user p…...
)
单例模式(懒汉式,饿汉式,变体)
单例模式,用于确保一个类只有一个实例,并提供一个全局访问点以访问该实例。 饿汉式(Eager Initialization) 程序启动时就创建实例 #include <iostream> class SingletonEager { private:static SingletonEager* instanc…...

Java Lambda表达式:简洁且强大的函数式编程工具
Lambda表达式是Java 8及以后版本中引入的一种函数式编程特性。它是一种匿名函数,允许开发人员以简洁和易读的方式编写代码,并且可以作为参数传递给方法或存储在变量中。Lambda表达式的基本语法如下:(parameters) -> expression,…...
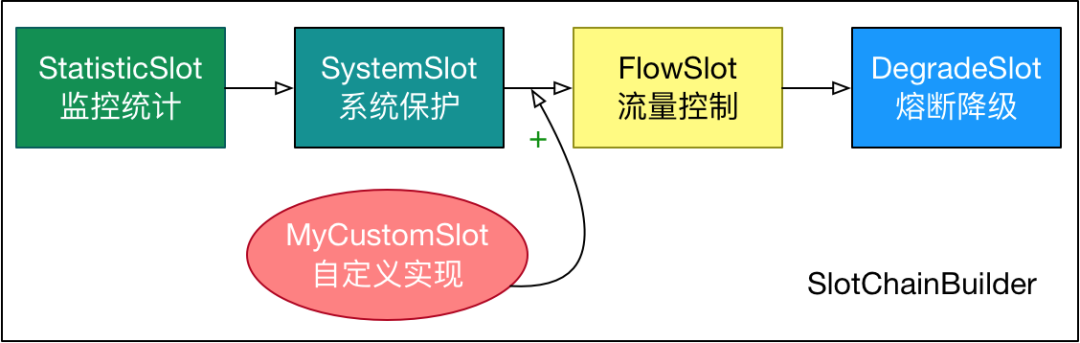
开源框架中的责任链模式实践
作者:vivo 互联网服务器团队-Wang Zhi 责任链模式作为常用的设计模式而被大家熟知和使用。本文介绍责任链的常见实现方式,并结合开源框架如Dubbo、Sentinel等进行延伸探讨。 一、责任链介绍 在GoF 的《设计模式》一书中对责任链模定义的:将…...
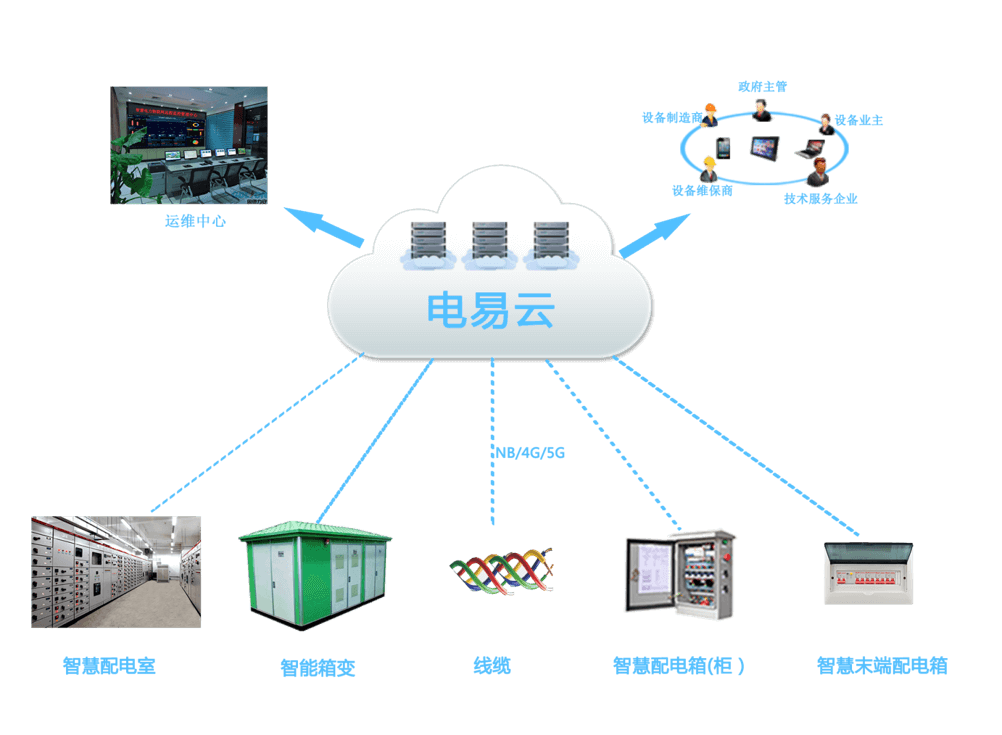
智能配电系统:保障电力运行安全、可控与高效
智能配电系统是一种先进的电力分配技术,它通过智能化、数字化和网络化等方式,有效地保障了电力运行的安全、可控和高效。 力安科技智能配电系统是在配电室(含高压柜、变压器、低压柜)、箱式变电站、配电箱及动力柜(…...
-每天学习10个知识)
MySQL学习系列(11)-每天学习10个知识
目录 1. 数据库设计的关键因素2. 使用存储过程和函数来提高性能和可重用性3. MySQL性能优化4. 使用视图简化查询和提供数据安全性5. 数据库备份和恢复策略的重要性和实践经验6. 在分布式系统中保证数据一致性和可用性7. 理解MySQL的复制和其在实际应用中的作用8. 使用游标进行分…...
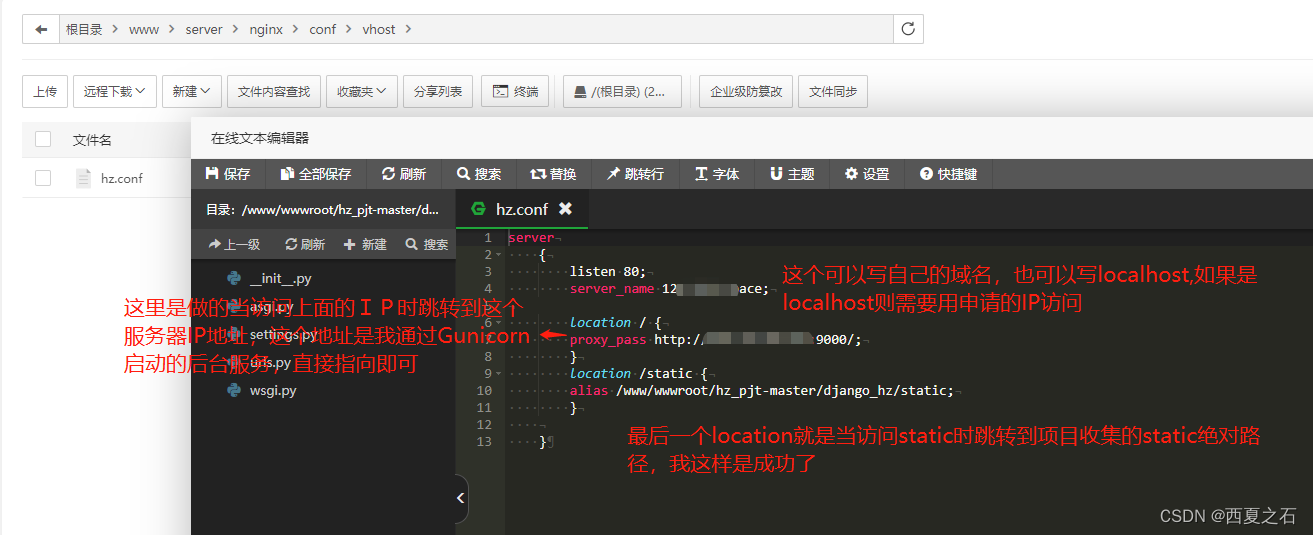
如何通过Gunicorn和Niginx部署Django
本文主要介绍如何配置Niginx加载Django的静态资源文件,也就是Static 1、首先需要将Django项目中的Settings.py 文件中的两个参数做以下设置: STATIC_URL /static/ STATIC_ROOT os.path.join(BASE_DIR, static) 然后在宝塔面板中执行python manage.…...
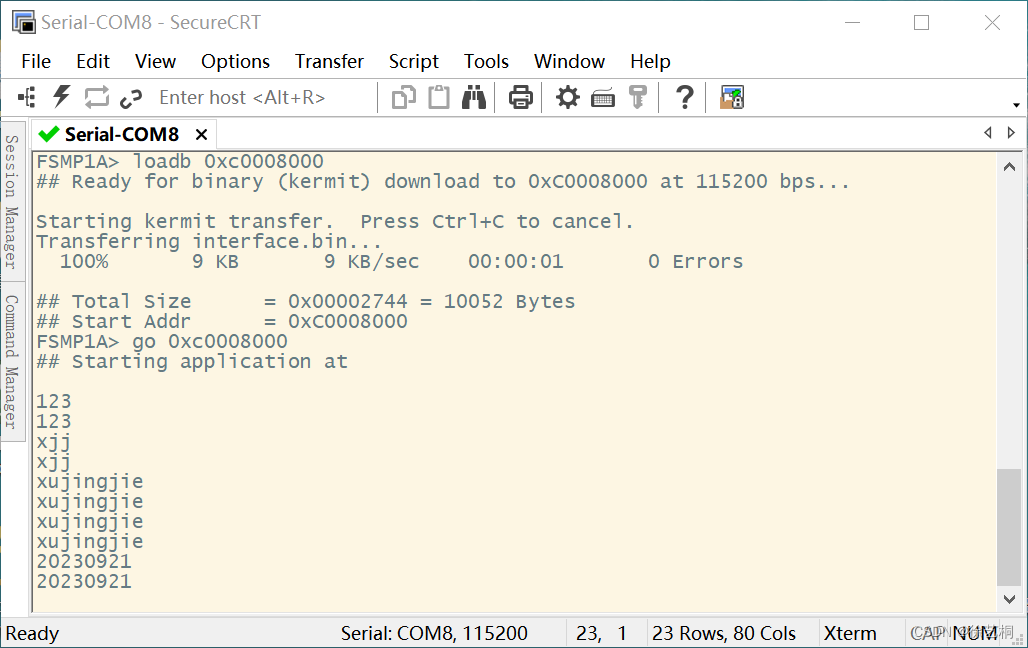
C语言 cortex-A7核UART总线实验
一、C 1)uart4.h #ifndef __UART4_H__ #define __UART4_H__ #include "stm32mp1xx_rcc.h" #include "stm32mp1xx_gpio.h" #include "stm32mp1xx_uart.h&quo…...

asp.net C#免费反编译工具ILSpy
在维护一个没有源码的C#项目,只能反编译了。 项目主页 https://github.com/icsharpcode/ILSpy 使用方法 中文界面使用简单,把你要反编译的dll拖过去就可以了。好使!!!...

演讲实录:DataFun 垂直开发者社区基于指标平台自主洞察北极星指标
在7月14日举办的 Kyligence 用户大会的数智新应用论坛上,DataFun COO 杜颖女士为大家带来了《垂直开发者社区基于指标平台自主洞察北极星指标》的主题演讲。接下来,我们一起看看 DataFun 如何在没有专门的 IT 团队的情况下,实现对北极星指标的…...
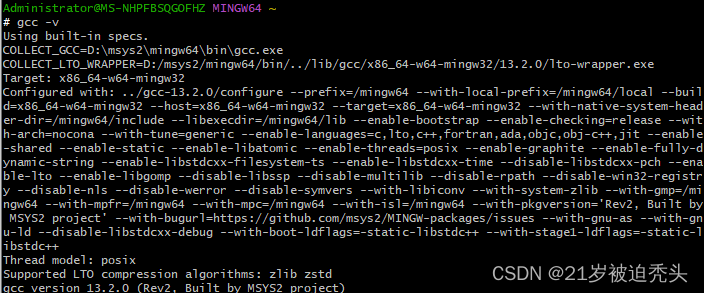
ffmpeg编译 Error: operand type mismatch for `shr‘
错误如下: D:\msys2\tmp\ccUxvBjQ.s: Assembler messages: D:\msys2\tmp\ccUxvBjQ.s:345: Error: operand type mismatch for shr D:\msys2\tmp\ccUxvBjQ.s:410: Error: operand type mismatch for shr D:\msys2\tmp\ccUxvBjQ.s:470: Error: operand type mismatch…...
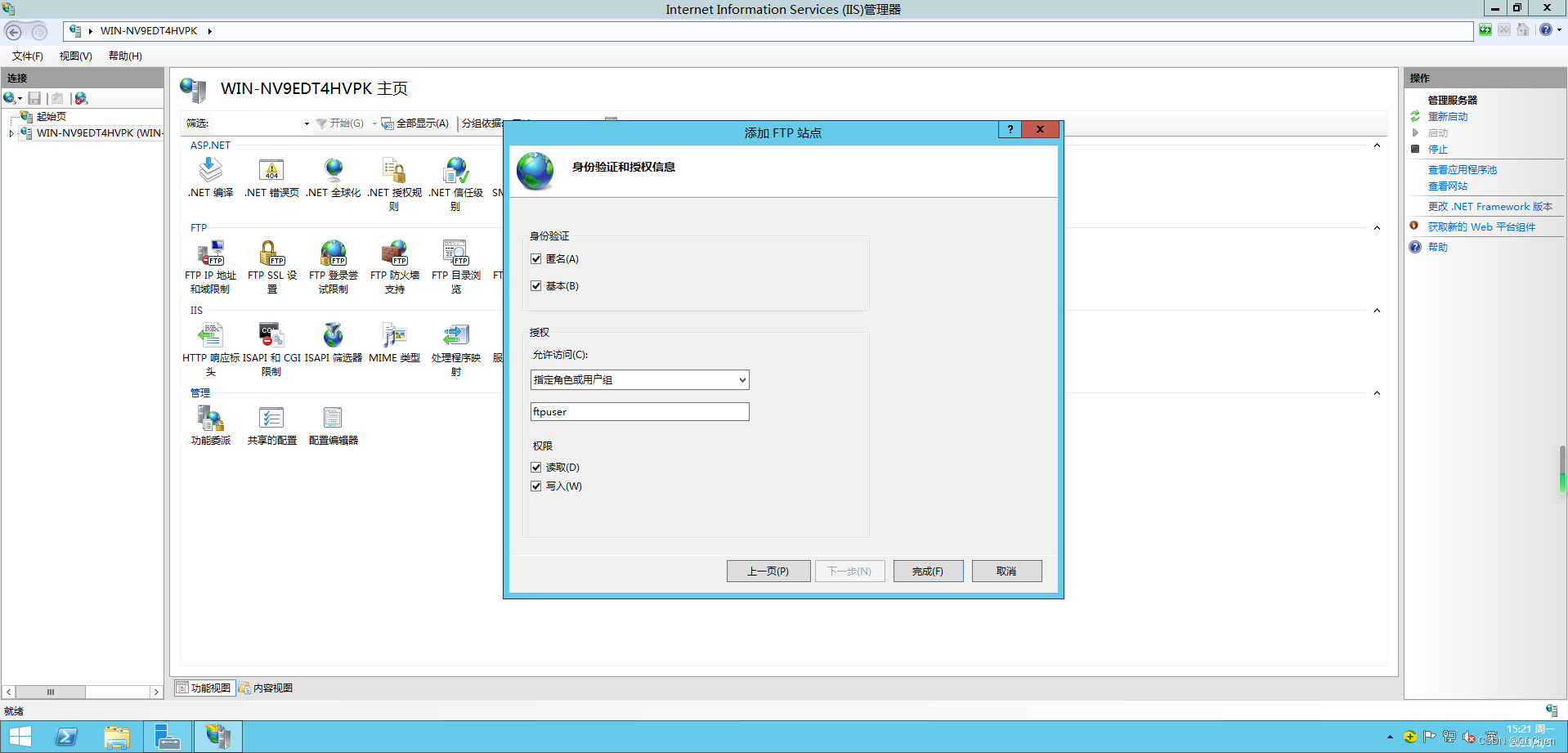
【Windows Server 2012 R2搭建FTP站点】
打开服务器管理器——添加角色和功能 下一步 下一步 下一步 选择FTP服务器,勾上FTP服务和FTP扩展,点击下一步 安装 安装完成关闭 打开我们的IIS服务器 在WIN-XXX主页可以看到我们的FTP相关菜单 右键WIN-XXXX主页,添加FTP站点 输入站点名称-FT…...

python教程:使用gevent实现高并发并限制最大并发数
嗨喽~大家好呀,这里是魔王呐 ❤ ~! python更多源码/资料/解答/教程等 点击此处跳转文末名片免费获取 import time import gevent from gevent.pool import Pool from gevent import monkey # 一,定义最大并发数 p Pool(20) # 二,导入gevent…...

借助reCAPTCHA实现JavaScript验证码功能
前言 验证码(CAPTCHA)是一种常见的安全验证机制,常用于区分真实用户和机器人。使用验证码可以有效防止恶意登录、自动注册或者密码爆破等攻击。本文将借助reCAPTCHA第三方库来实现JavaScript验证码功能。 验证码的原理 验证码的核心思想是要…...
监控数据的采集方式及原理
采集方法使用频率从高到低依次是读取 /proc目录、执行命令行工具、远程黑盒探测、拉取特定协议的数据、连接到目标对象执行命令、代码埋点、日志解析。 读取 /proc目录 /proc是一个位于内存中的伪文件系统,而在该目录下保存的不是真正的文件和目录,而是…...

Vue路由与node.js环境搭建
目录 前言 一.Vue路由 1.什么是spa 1.1简介 1.2 spa的特点 1.3 spa的优势以及未来的挑战 2.路由的使用 2.1 导入JS依赖 2.2 定义两个组件 2.3 定义组件与路径对应关系 2.4 通过路由关系获取路由对象 2.5 将对象挂载到vue实例中 2.6 定义触发路由事件的按钮 2.7 定…...
腾讯云16核服务器性能测评_轻量和CVM配置大全
腾讯云16核服务器配置大全,CVM云服务器可选择标准型S6、标准型SA3、计算型C6或标准型S5等,目前标准型S5云服务器有优惠活动,性价比高,计算型C6云服务器16核性能更高,轻量16核32G28M带宽优惠价3468元15个月,…...
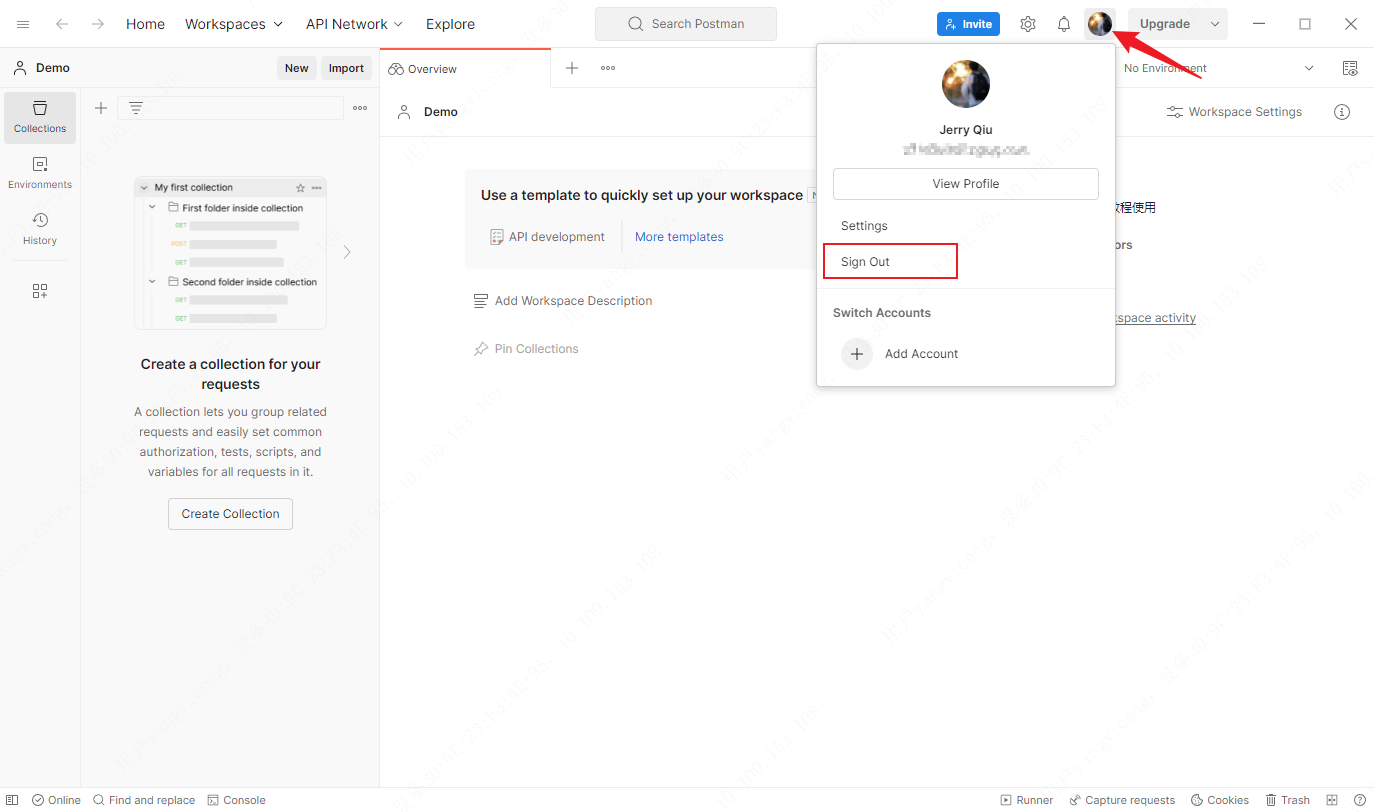
Postman应用——下载注册和登录
文章目录 下载安装注册登录注册账号登录账号 下载安装 Postman下载:https://www.postman.com/ 访问链接后,进入首页,根据自己的操作系统下载对应的版本。 找到下载到的目录直接双击.exe文件,会默认安装在C盘,安装完会…...

uni-app混合开发 navigateTo、reLaunch、redirectTo、switchTab区别
1.navigateTo 保留当前页面,跳转到应用内的某个页面,使用uni.navigateBack可以返回到原页面。 要注意的是navigateTo只能跳转的应用内非 tabBar 的页面的路径 , 路径后可以带参数;如果跳转url参数为tabBar的路径则无法进行跳转 2.redir…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...
