Hyperloglog
一,前言
在互联网行业中存在两个比较重要的指标:PV(页面访问量)和 UV(用户访问量)
如果有这样的一个业务:
统计PV,那么你会怎么做?
我们可以使用Redis的incr、incrby指令,给每个网页配置一个独立Redis计数器就可以了,把这个技术区的key后缀加上当它的日期,这样一个请求过来,就可以通过执行incr、incrby指令统计所有PV。
那么统计UV又该怎么做呢?
UV和PV不同,UV需要对同一用户的访问进行去重,此时很快就能想到使用Redis中的set来存储,但是会面临以下问题:
- 对于数据量越来越大,存储数据的空间占用越来越大
- 统计的性能比较慢,虽然可以通过异步方式统计,但是性能并不理想
因此引入了Redis的新数据类型HyperLogLog。
二,Hyperloglog简介
HyperLogLog 是一种概率数据结构,用于在恒定的内存大小下估计集合的基数(不同元素的个数)。它不是一个独立的数据类型,而是一种特殊的 string 类型,它可以使用极小的空间来统计一个集合中不同元素的数量,也就是基数。在Redis中,每个HyperLogLog键只需要花费12KB内存,就可以计算接近2^64个不同的基数。(为什么是12KB呢?下面会详细讲解)
hyperloglog 类型的底层实现是 SDS(simple dynamic string),它和 string 类型相同,只是在操作时会使用一种概率算法来计算基数。hyperloglog 的误差率为 0.81%,也就是说如果真实基数为 1000,那么 hyperloglog 计算出来的基数可能在 981 到 1019 之间
三,Redis中Hyperloglog的使用
PFADD key element [element …]
将任意数量的元素添加到指定的 HyperLogLog 里面,当PFADD key element [element …]指令执行时,如果HyperLogLog的估计近似基数在命令执行之后出现了变化,那么命令返回1,否则返回0,如果HyperLogLog命令执行时给定的键不存在,那么程序将先创建一个空的HyperLogLog结构,再执行命令。
该命令可以只给定key不给element,这种以方式被调用时:
如果给定的键存在且已经是一个HyperLogLog,那么这种调用不会产生任何效果
如果给定的键不存在,那么命令会创建一个空的HyperLogLog,并且给客户端返回1
返回值:
如果HyperLogLog数据结构内部存储的数据被修改了,那么返回1,否则返回0
时间复杂度:O(1)
PFCOUNT key [key …]
PFCOUNT 指令后面可以跟多个key,当PFCOUNT key [key …]命令作用于单个键时,返回存储在给定键的HyperLogLog的近似基数,如果键不存在,则返回0;当PFCOUNT key [key …]命令作用于多个键时,返回所给定HyperLogLog的并集的近似基数,这个近似基数是通过将索引给定HyperLogLog合并至一个临时HyperLogLog来计算得出的。
返回值:返回给定HyperLogLog包含的唯一元素的近似数量的整数值
时间复杂度:当命令作用于单个HyperLogLog时,时间复杂度为O(1),并且具有非常低的平均常数时间。当命令作用于N个HyperLogLog时,时间复杂度为O(N),常数时间会比单个HyperLogLog要大的多。
PFMERGE destkey sourcekey [sourcekey …]
将多个HyperLogLog合并到一个HyperLogLog中,合并后HyperLogLog的基数接近于所有输入HyperLogLog的可见集合的并集,合并后得到的HyperLogLog会被存储在destkey键里面,如果该键不存在,那么命令在执行之前,会先为该键创建一个空的HyperLogLog。
返回值:字符串回复,返回OK
时间复杂度:O(N),其中N为被合并的HyperLogLog的数量,不过这个命令的常数复杂度比较高
四,Hyperloglog原理
Hyperloglog基于概率论中的伯努利试验并结合了极大似然估算方法,并进行了分桶优化。
1. 伯努利试验
在认识为什么Hyperloglog能够使用极少的内存(12K)来统计巨量的数据之前,先认识一下伯努利试验。
伯努利试验是数学概率论中的一部分内容,它的典故来源于抛硬币。
硬币拥有正反两面,一次的上抛至落下,最终出现正反面的概率都是50%。假设一直抛硬币,直到它出现正面为止,我们记录为一次完整的试验,间中可能抛了一次就出现了正面,也可能抛了4次才出现正面。无论抛了多少次,只要出现了正面,就记录为一次试验。这个试验就是伯努利试验。
那么对于多次的伯努利试验,假设这个多次为n次。就意味着出现了n次的正面。假设每次伯努利试验所经历了的抛掷次数为k。第一次伯努利试验,次数设为k1,以此类推,第n次对应的是kn。
其中,对于这n次伯努利试验中,必然会有一个最大的抛掷次数k,例如抛了12次才出现正面,那么称这个为k_max,代表抛了最多的次数。
伯努利试验容易得出有以下结论:
- n 次伯努利过程的投掷次数都不大于 k_max。
- n 次伯努利过程,至少有一次投掷次数等于 k_max
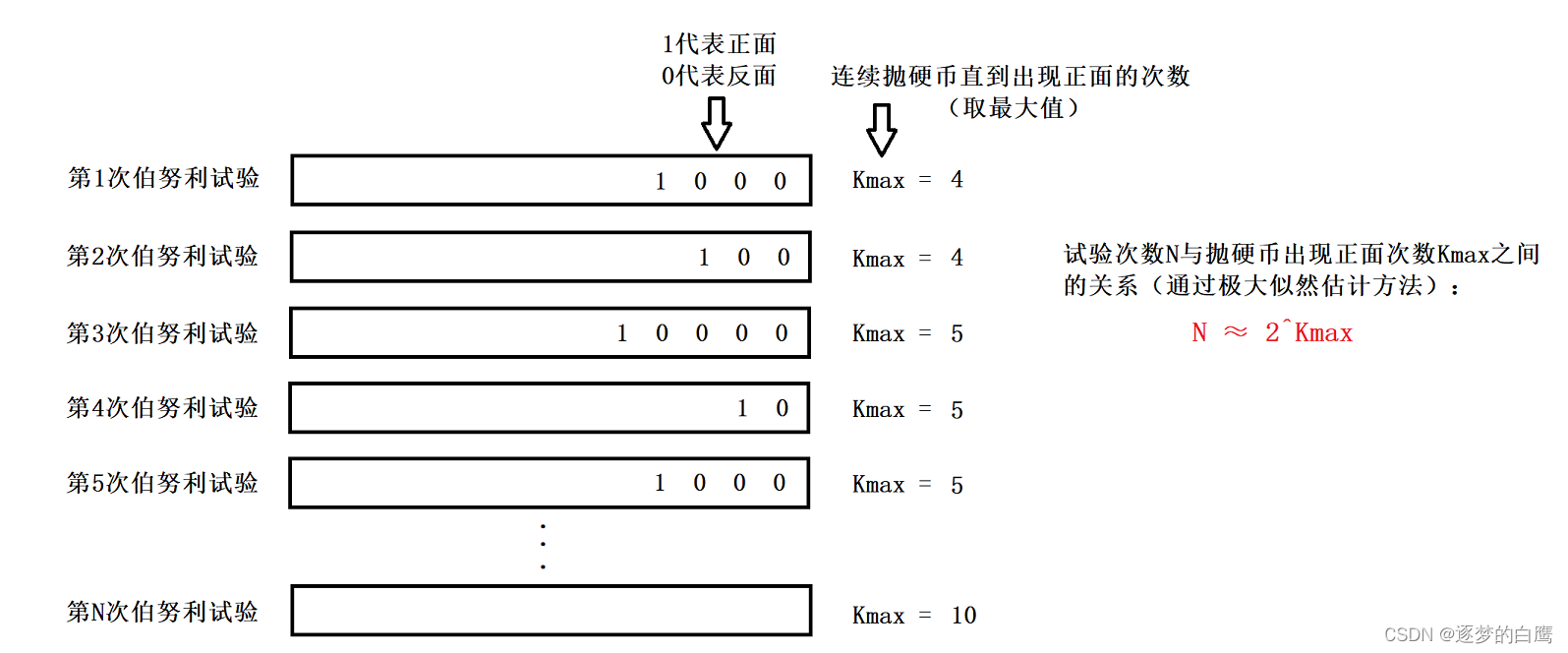
上述案例可以看出,假设n=3,此时通过估算关系n=2^kmax,2^5 ≠3,而且偏差很大。因此得出结论,这种估算方法误差很大。
2. 估值优化
关于上述估值偏差较大的问题,可以采用如下方式结合来缩小误差:
- 增加测试的轮数,取平均值。假设三次伯努利试验为1轮测试,我们取出这一轮试验中最大的的kmax作为本轮测试的数据,同时我们将测试的轮数定位100轮,这样我们在100轮实验中,将会得到100个kmax,此时平均数就是(k_max_1 + … + k_max_m)/m,这里m为试验的轮数,此处为100.
- 增加修正因子,修正因子是一个不固定的值,会根据实际情况来进行值的调整。
上述这种增加试验轮数,取Kmax的平均值的方法,是loglog算法的实现。因此loglog它的估算公式如下:
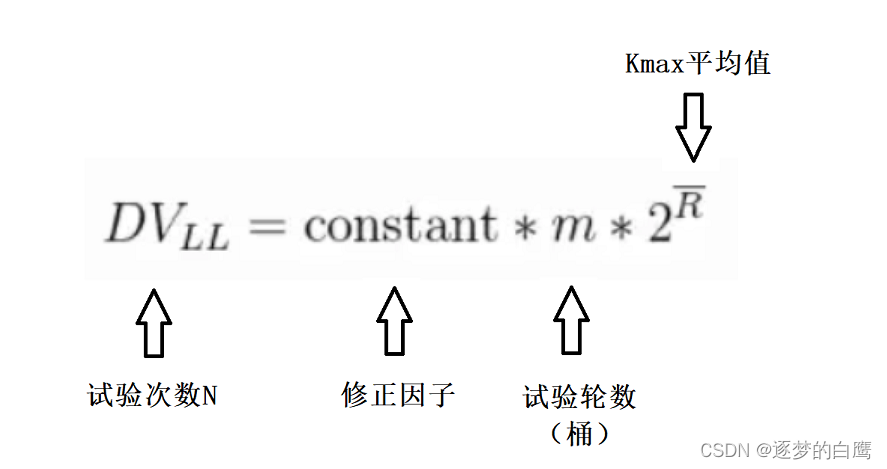
loglog与Hyperloglog的区别在于:loglog采用算数平均数,而Hyperloglog采用调和平均数
调和平均数:
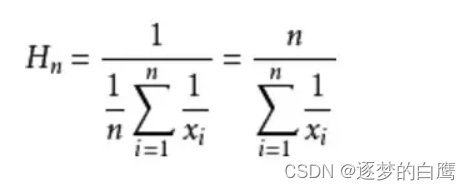
调和平均数的效果更好,例如以下例子:
一个小区内有100户,现在要统计小区的平均工资,小区的工资可以分为大致6000左右,10000左右的,还有一户100000000以上。
此时使用算数平均会导致结果和现实相差很大。
使用调和平均:那户工资上100000000的,对整体的影响就几乎可以忽视。
3. Hyperloglog实现原理
图示:
Redis中Hyperloglog前14位进行分桶,后50位进行获取Kmax
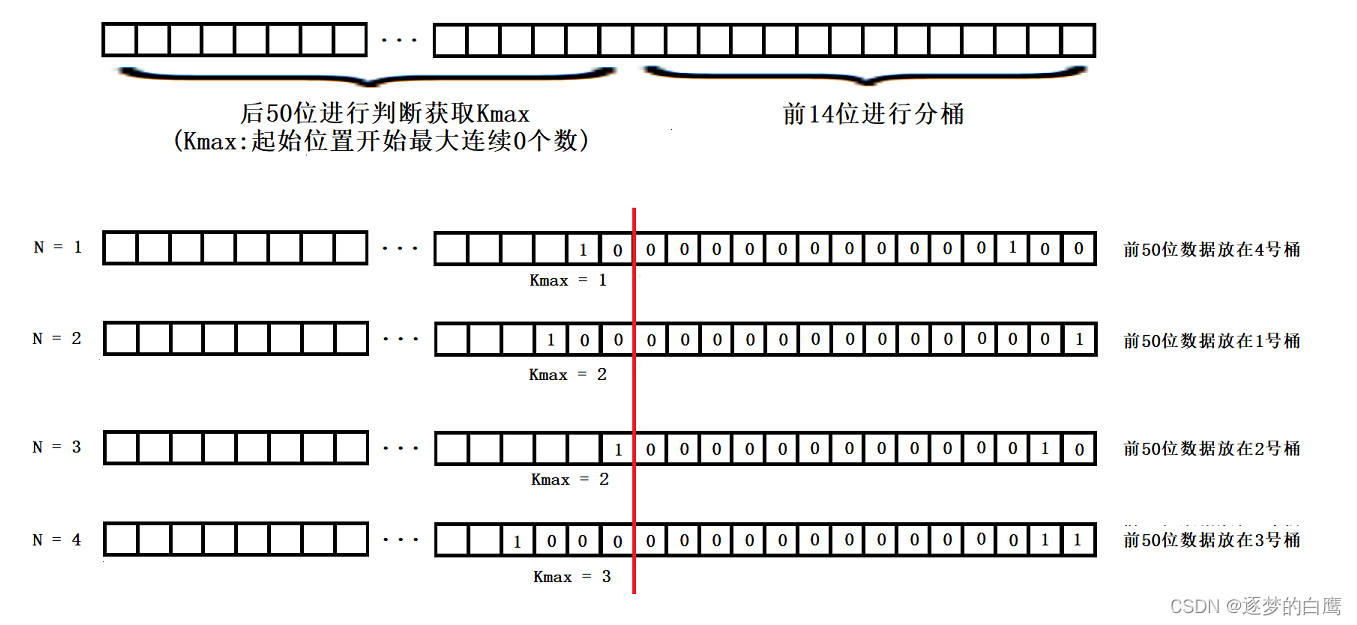
3.1 将数据转化为bit串
通过Hash函数,将数据转为64位的比特串,例如输入5,便转为:101。为什么要这样转化呢?
是因为要和抛硬币对应上,比特串中,0 代表了反面,1 代表了正面,如果一个数据最终被转化了 10010000,那么从右往左,从低位往高位看,我们可以认为,首次出现 1 的时候,就是正面。
那么基于上面的估算结论,我们可以通过多次抛硬币实验的最大抛到正面的次数来预估总共进行了多少次实验,同样也就可以根据存入数据中,转化后的出现了 1 的最大的位置 Kmax 来估算存入了多少数据。
3.2 分桶
分桶就是分多少轮。在抛硬币中我们可以将三次实验分为一组,用这一组的Kmax求平均值当作一次的Kmax,这样可以减少误差。
抽象到计算机存储中去,就是存储的是一个以单位是比特(bit),长度为 L 的大数组 S ,将 S 平均分为 m 组,注意这个 m 组,就是对应多少轮,然后每组所占有的比特个数是平均的,设为 P。容易得出下面的关系:
- L = S.length
- L = m * p
- 以 K 为单位,S 占用的内存 = L / 8 / 1024
为什么Hyperloglog大小为12K?

由上图可知:
- 后14位用于分桶,也就是需要2^14 = 16384个桶(0~16383,也就是14位全0~全1)
- 每个桶子需要存储前50位得到的Kmax值(起始开始最多连续零个数),而50位最多有50个0,因此Kmax最大取到50,2^6 = 64 > 50,因此每个桶只需要6个bit位就可以保存Kmax
- 每8个bit位为1字节,每1024字节为1K
综合以上两点:Hyperloglog的大小 = 16384 * 6 / 8 * 1024 = 12K
3.3 Hyperloglog估算公式
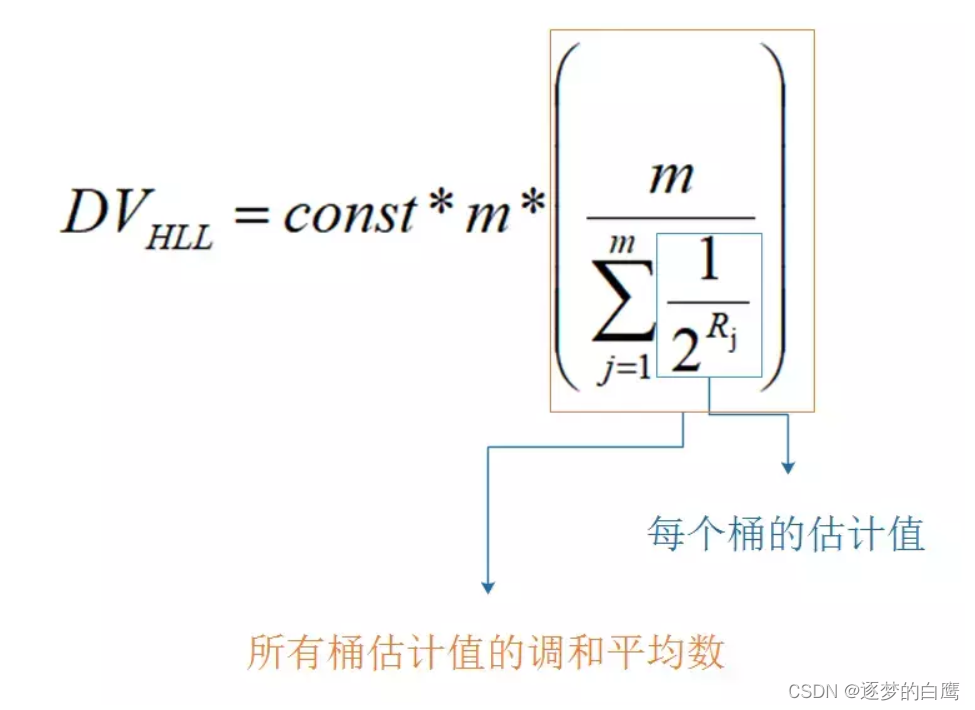
五,Hyperloglog的优缺点
优点:内存占用很小只有12K
缺点:存在误差概率。不能存储元素本身,只能统计集合基数值。
六,Hyperloglog适用场景
-
统计一个
APP的日活、月活数; -
统计一个页面的每天被多少个不同账户访问量(Unique Visitor,UV);
-
统计用户每天搜索不同词条的个数;
-
统计注册 IP 数。
七,布隆过滤器,布谷鸟过滤器,Hyperloglog如何选择
可以设置误判率:布隆过滤器
可以进行删除操作:布谷鸟过滤器
占用空间小:Hyperloglog
相关文章:

Hyperloglog
一,前言 在互联网行业中存在两个比较重要的指标:PV(页面访问量)和 UV(用户访问量) 如果有这样的一个业务: 统计PV,那么你会怎么做? 我们可以使用Redis的incr、incrby指…...

如何自动获取短信验证码?
点击下方关注我,然后右上角点击...“设为星标”,就能第一时间收到更新推送啦~~~ 这篇文章通过解决实际项目开发中遇到的如何自动获取短信验证码的问题,进一步讲述在Java中如何使用正则。 Java中如何使用正则 Java中正则相关类位于java.util.r…...
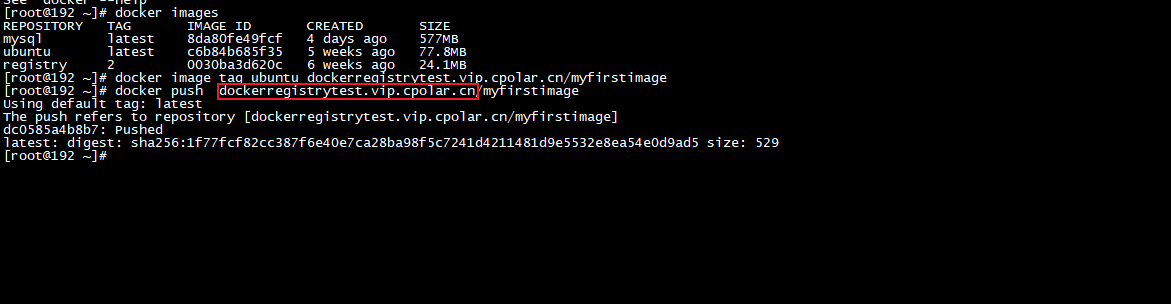
Linux 本地 Docker Registry本地镜像仓库远程连接【内网穿透】
Linux 本地 Docker Registry本地镜像仓库远程连接 文章目录 Linux 本地 Docker Registry本地镜像仓库远程连接1. 部署Docker Registry2. 本地测试推送镜像3. Linux 安装cpolar4. 配置Docker Registry公网访问地址5. 公网远程推送Docker Registry6. 固定Docker Registry公网地址…...

基于Yolov8的工业小目标缺陷检测(4):SPD-Conv,低分辨率图像和小物体涨点明显
💡💡💡本文改进:SPD-Conv,处理低分辨率图像和小物体等更困难的任务时效果明显。 SPD-Conv | 亲测在工业小目标缺陷涨点明显,原始mAP@0.5 0.679提升至0.775 收录专栏: 💡💡💡深度学习工业缺陷检测 :http://t.csdn.cn/fVSgs ✨✨✨提供工业缺陷检测性能提升…...
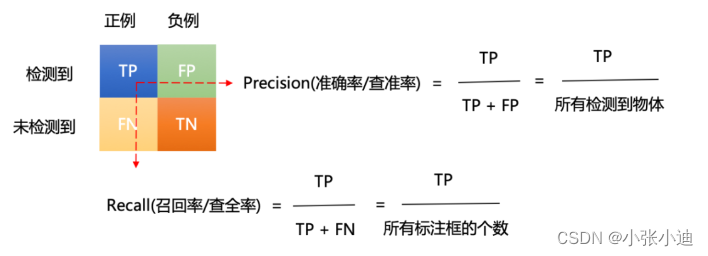
平均精度(AP)
什么是平均精度(AP) 平均精度 (AP)并不是精度 (P)的平均值。 平均精度 (AP) 是按类别计算的。 mAP(mean average precision)是一个平均值,常用作目标检测中的检测精度指标mAP 指标通过对于一个平均目标来检测任务中多个目标所对应不同 AP&a…...

建议收藏《Verilog代码规范笔记_华为》(附下载)
华为verilog编程规范是坊间流传出来华为内部的资料,其贴合实际工作需要,是非常宝贵的资料,希望大家善存。至于其介绍,在此不再赘述,大家可看下图详细了解,感兴趣的可私信领取《Verilog代码规范笔记_华为》。…...
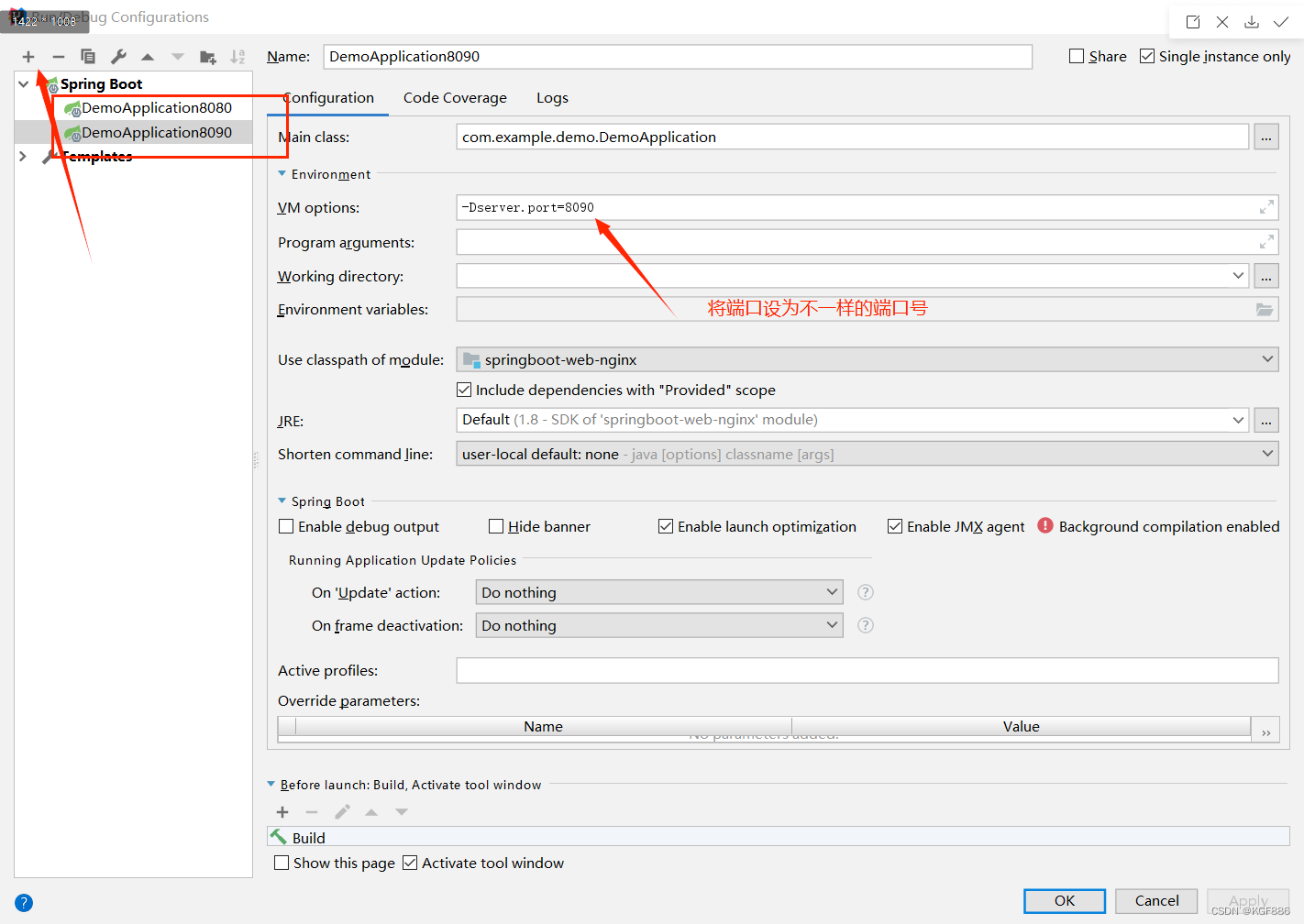
Nginx环境搭建、负载均衡测试
Nginx环境搭建、负载均衡测试 系统环境: win10,IDEA2020,JDK8 一、nginx环境搭建 1.ngxin下载 Nginx官网下载: http://nginx.org/en/download.html Nginx有三种版本,分别是Mainline version(开发版&…...
软件工程知识总结梳理
🔥🔥宏夏Coding网站,致力于为编程学习者、互联网求职者提供最需要的内容!网站内容包括求职秘籍,葵花宝典(学习笔记),资源推荐等内容。在线阅读:https://hongxiac.com&…...
Mybatis自动映射Java对象 与 MySQL8后的JSON数据
文章目录 Mybatis自动映射Java对象 与 MySQL8后的JSON数据1.转化成为正常Json类型1.1 JsonTypeHander1.2 ListJsonTypeHandler 负责List<T> 类型1.3 实体类1.4 mapper1.5 测试类 2. 存储为携带类型的Json Mybatis自动映射Java对象 与 MySQL8后的JSON数据 1.转化成为正常…...

【JavaScript】深拷贝和浅拷贝
在 JavaScript 中,深拷贝(Deep Copy)和浅拷贝(Shallow Copy)是两种不同的对象复制方法,它们涉及到如何复制对象的属性以及如何处理对象内部的嵌套引用。以下是它们的解释: 浅拷贝(S…...
【SLAM】10.纵观SLAM,对比方案和未来方向
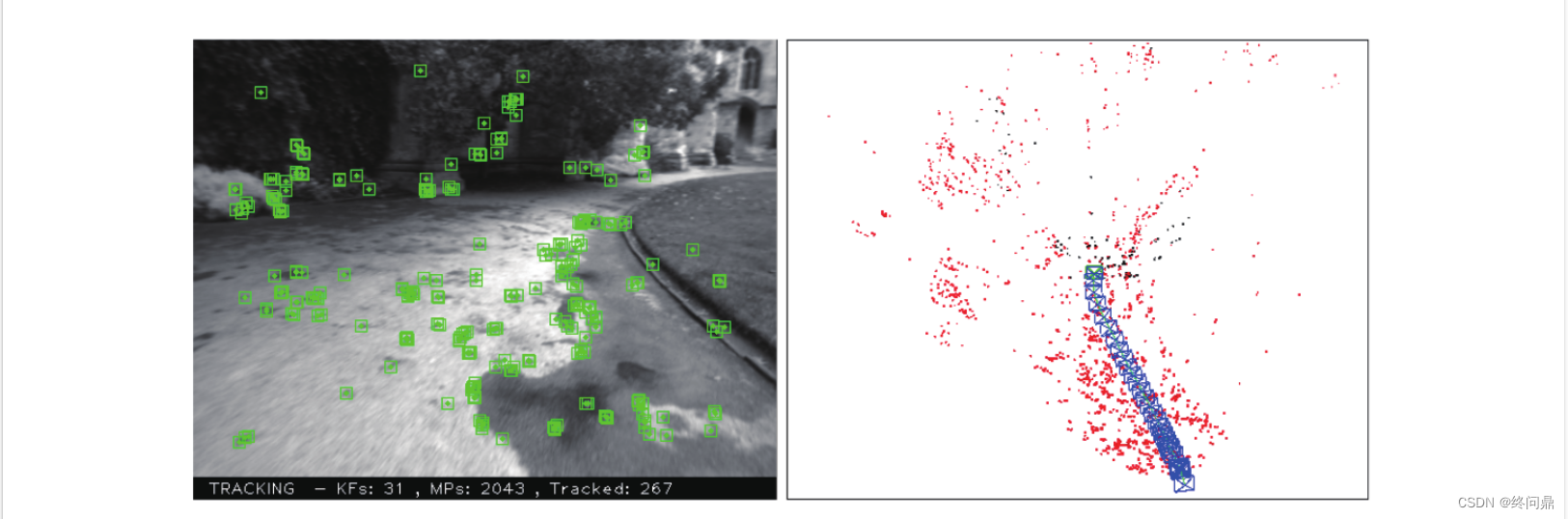
"天下谁人配白衣” SLAM方案研究方向 SLAM方案 站在历史角度,看一下为SLAM的发展带来贡献的方案: 2007年—A.J.Davison—MonoSLAM 视觉SLAM的先驱,建立在EKF基础上,此前基本无法在线运行,意义较大;…...

PyTorch中DistributedDataParallel使用笔记
1. 基本概念 在使用DistributedDataParallel时有一些概率必须掌握 多机多卡含义world_size代表有几台机器,可以理解为几台服务器rank第几台机器,即第几个服务器local_rank某台机器中的第几块GPU 单机多卡含义world_size代表机器一共有几块GPUrank第几…...
)
前端面试的话术集锦第 18 篇博文——高频考点(HTTP协议 TLS协议)
这是记录前端面试的话术集锦第十八篇博文——高频考点(HTTP协议 & TLS协议),我会不断更新该博文。❗❗❗ 1. HTTP 请求中的内容 HTTP请求由三部分构成,分别为: 请求行 首部 实体 请求行大概长这样GET /images/logo.gif HTTP/1.,基本由请求方法、URL、协议版本组成,…...
SQL Server 数据库变成单个用户怎么办
参考技术A 1、首先我们打开SQL SERVER的管理控制台,找到一个要设置角色的用户。 2、下面我们将为这个用户赋予创建数据库的角色,我们先用这个用户登录管理工具看一下是否具有创建用户的权限。 3、进行数据库创建的时候,提示如下的错误&…...
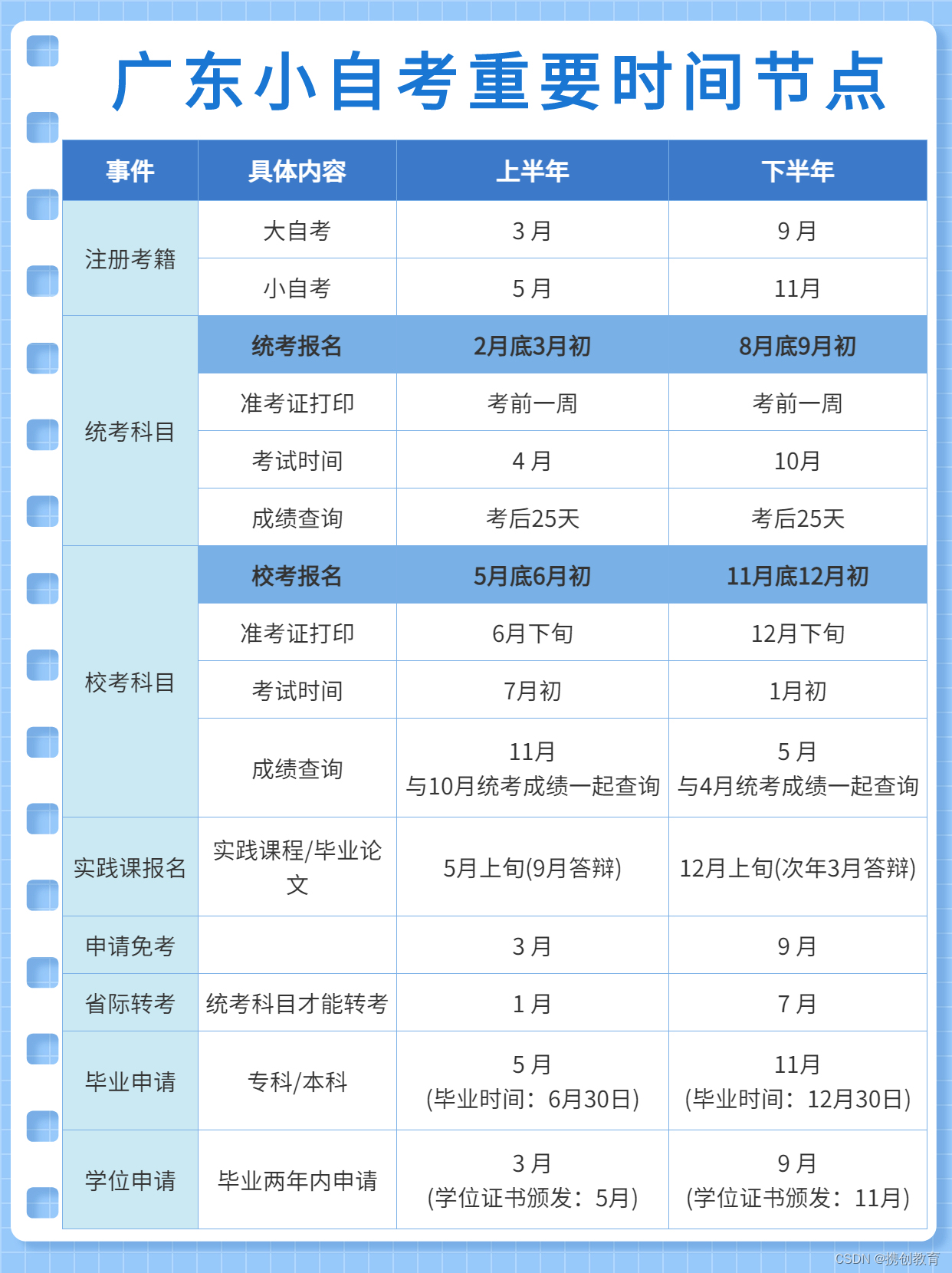
错过成考报名,今年你还有这两种方式升学!
2023年广东成人高考已经报名结束啦 错过报名或没有抢到考位的同学不用伤心 你还有另外两个提升学历的机会 开放大学or小自考 今天一起来了解一下吧~ 什么是开放大学? 开放教育其实也就是开放大学,也就是我们所说的中央广播电视大学,现在…...
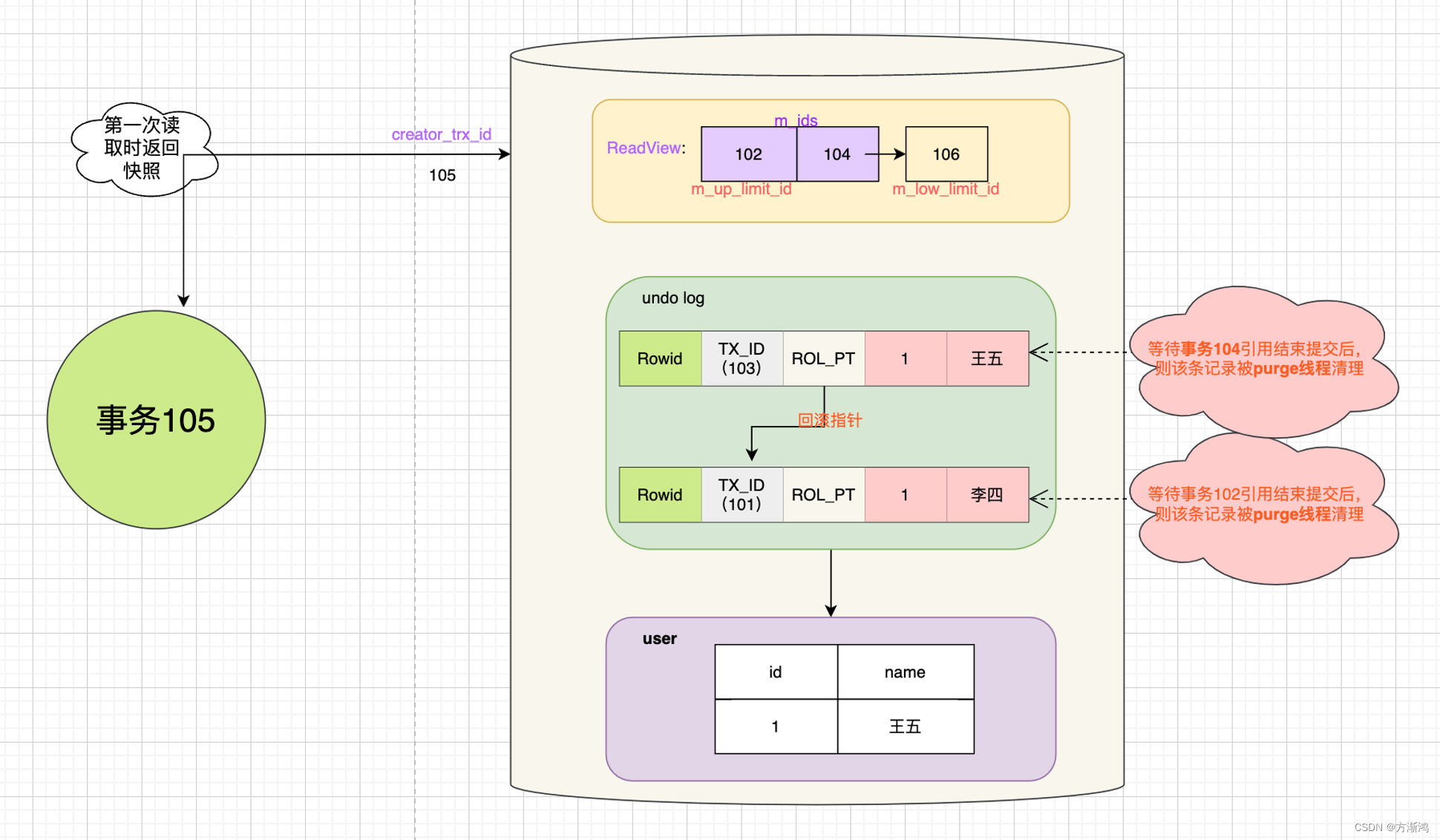
【2023】从事务的特征以及解决方式上分析MySQL是如何保证事务的
----以MySQL的InnoDB介绍 目录 前言事务,事务到底是什么? 一、事务的特征:二、事务特征具体保证1、Redo Log(重做日志) ---保证事务的持久性1.1、🟡刷盘时机1.2、redo log记录形式1.3、redo log日志的好处 2、undo log(回滚日志)…...
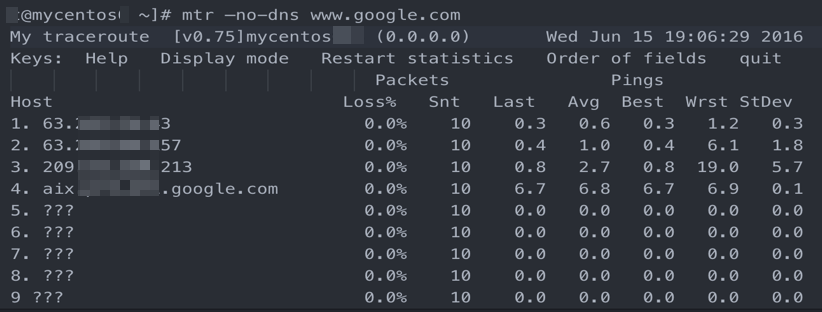
MTR 网络连通性测试工具 基础入门 整理
MTR MTR的全称是 my traceroute,是一个集合了 ping 与 traceroute 功能的网络诊断工具,广泛应用于链路测试。相对于 traceroute 只会做一次链路跟踪测试,mtr会对链路上的相关节点做持续探测并给出相应的统计信息。因此,mtr能避免…...

Linux安装mysql数据库并实现主从搭建
一.环境说明 【环境说明】: 192.168.110.161 mysql-master ##网络配置到位,防火墙关闭,selinux关闭 192.168.110.162 mysql-slave ##网络配置到位,防火墙关闭,selinux关闭 两台主机,操作系统是centos7…...

windows使用小技巧之windows照片查看器无法显示此图片
碰到过好几次了,以前没有理会,今天特意去查了一下解决方法,不然确实不太方便。 1、打开“颜色管理”-“高级”: 2、将“设备配置文件”选择为“Agfa:Swop Standard” 3、关闭,重新打开图片,好…...

ez_pz_hackover_2016
ez_pz_hackover_2016 Arch: i386-32-little RELRO: Full RELRO Stack: No canary found NX: NX disabled PIE: No PIE (0x8048000) RWX: Has RWX segments32位,保护全关 int chall() {size_t v0; // eaxint result; // eaxchar s[1024]…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...

push [特殊字符] present
push 🆚 present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中,push 和 present 是两种不同的视图控制器切换方式,它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...

苹果AI眼镜:从“工具”到“社交姿态”的范式革命——重新定义AI交互入口的未来机会
在2025年的AI硬件浪潮中,苹果AI眼镜(Apple Glasses)正在引发一场关于“人机交互形态”的深度思考。它并非简单地替代AirPods或Apple Watch,而是开辟了一个全新的、日常可接受的AI入口。其核心价值不在于功能的堆叠,而在于如何通过形态设计打破社交壁垒,成为用户“全天佩戴…...

关于easyexcel动态下拉选问题处理
前些日子突然碰到一个问题,说是客户的导入文件模版想支持部分导入内容的下拉选,于是我就找了easyexcel官网寻找解决方案,并没有找到合适的方案,没办法只能自己动手并分享出来,针对Java生成Excel下拉菜单时因选项过多导…...
