排序算法-----归并排序
目录
前言:
归并排序
1. 定义
2.算法过程讲解
2.1大致思路
2.2图解示例
拆分合成步骤
编辑
相关动态图
3.代码实现(C语言)
4.算法分析
4.1时间复杂度
4.2空间复杂度
4.3稳定性
前言:
今天我们就开始学习新的排序算法----归并排序,说到归并排序,最重要的思想就是分而治之,先分后治。相较于前面所学过的排序算法,归并排序过程相对比较复杂,但是不要慌!我会详细讲解这个过程的!下面我们就一起来学习吧!

归并排序
1. 定义
归并排序是建立在归并操作上的一种有效,稳定的排序算法,该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并
2.算法过程讲解
2.1大致思路
已知一个数组arr[0,n-1],实现对这个数组进行拆分为arr[0,n/2]和arr[n/2+1,n-1]然后对这个数组进行进一步对半拆分,直到拆成每个分数组里面只有一个元素时,结束拆分;然后进入排序,按照拆分过程的路径进行排序合并,直到合并为一个数组的时候结束,最终得到的数组就是排序完成的数组。
归并排序是用分治思想,分治模式在每一层递归上有三个步骤:
- 分解(Divide):将n个元素分成个含n/2个元素的子序列。
- 解决(Conquer):用合并排序法对两个子序列递归的排序。
- 合并(Combine):合并两个已排序的子序列已得到排序结果
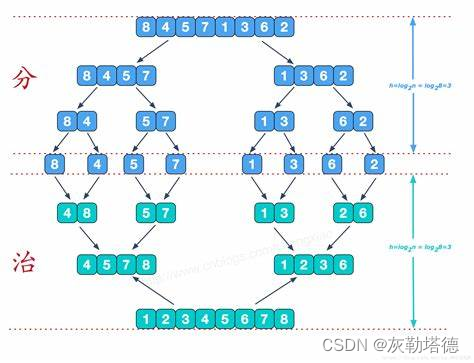
2.2图解示例
拆分合成步骤
已知一个数组 [6,5,3,1,8,7,2,4],要求通过归并排序进行排序
第一步,依次拆分,直到每一个分数组剩下一个元素 ,如下所示:
6 5 3 1 8 7 2 4
第一次拆分 6 5 3 1 8 7 2 4
第二次拆分 6 5 3 1 8 7 2 4
第三次拆分 6 5 3 1 8 7 2 4
第二步,拆分完成之后,就进行排序 合并,如下所示:
6 5 3 1 8 7 2 4
第一次合并: 5 6 1 3 7 8 2 4
第二次合并: 1 3 5 6 2 4 7 8
第三次合并: 1 2 3 4 5 6 7 8
以上步骤就完成了归并排序的过程了,演示图如下所示:
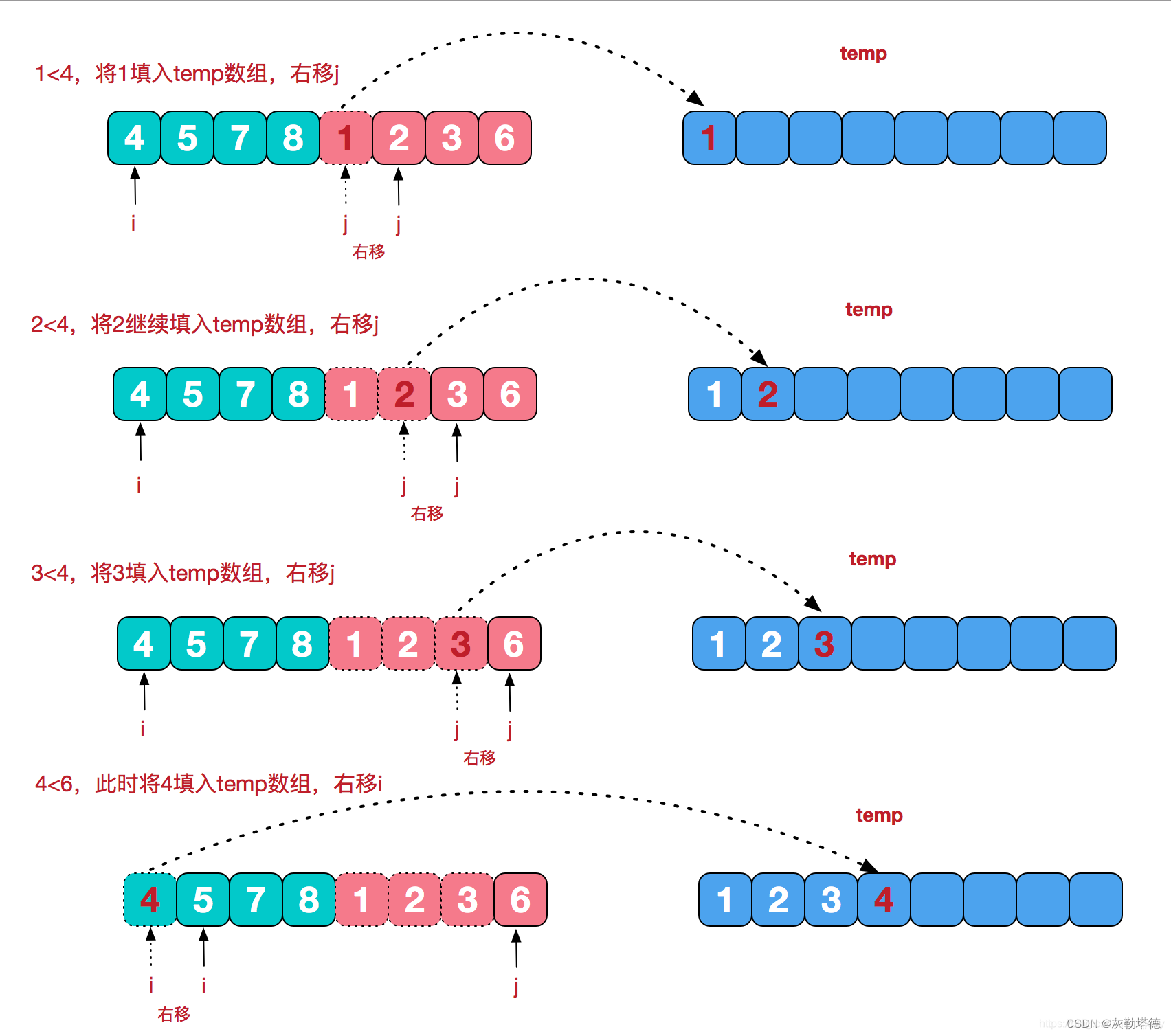
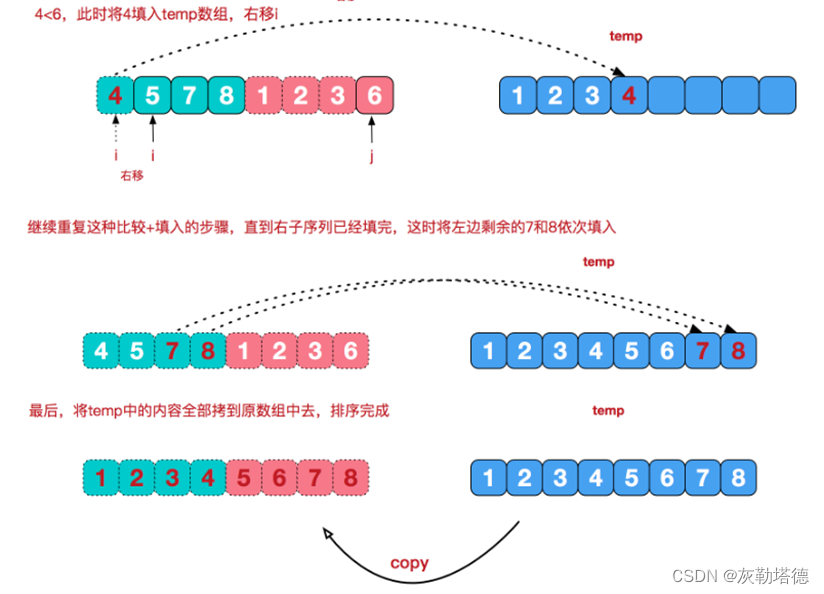 动态图:
动态图:
相关动态图
3.代码实现(C语言)
#include<stdio.h>
//归并排序
//合成排序
void merge(int* n,int *temp,int left,int mid,int rigth) {int l_pos = left;int r_pos = mid+1;int pos = left;//左右两部分数组进行比较合并while (l_pos <= mid && r_pos <= rigth) {if (n[l_pos] < n[r_pos])temp[pos++] = n[l_pos++];elsetemp[pos++] = n[r_pos++];}//如果左边还有多余的就直接补到后面去while (l_pos <= mid)temp[pos++] = n[l_pos++];//如果右边有多余的就直接补到后面去while (r_pos <= rigth)temp[pos++] = n[r_pos++];//这里只需要把原来的数组覆盖掉就行了while (left <= rigth) {n[left] = temp[left];left++;}}
//拆分与归并
void msort(int *n,int *temp,int left,int right) {if (left < right) { int mid = (left + right) / 2; //先拆分为两部分msort(n, temp, left, mid); //左边递归msort(n, temp, mid+1, right);//右半递归merge(n, temp, left, mid, right); //拆分完成之后进行归并和排序}
}
//排序函数接口
void merge_sort(int* n, int length) {int* temp = (int*)malloc(sizeof(int) * length);//申请一个同样大小的辅助数组空间if (temp) {//如果申请成功msort(n, temp, 0, length-1); //进入到排序free(temp); //释放掉这个空间}else {printf("Space allocation failure");}
}int main() {int array[8] = { 25,24,6,65,11,43,22,51 };printf("排序前:");for (int i = 0; i < sizeof(array) / sizeof(int); i++) {printf("%d ", array[i]);}printf("\n排序后:");merge_sort(array, sizeof(array) / sizeof(int));for (int i = 0; i < sizeof(array) / sizeof(int); i++) {printf("%d ", array[i]);}
}
//排序前:25 24 6 65 11 43 22 51
//排序后:6 11 22 24 25 43 51 654.算法分析
4.1时间复杂度
归并排序的速度仅次于快速排序,速度是相当快的。因为归并排序每次都是在相邻的数据中进行操作,所以归并排序时间复杂度为O(nlogn)。
4.2空间复杂度
你知道么,归并排序在任何情况下的时间复杂度永远都是 O(nlogn),是不是很奇怪呢?别急,凡事有得必有失,归并排序是通过牺牲空间的代价来实现减小时间复杂度的。上面的代码涉及到数据暂存空间的开辟,其开辟的空间数量最大也不会超过n,所以空间复杂度为O(n)
4.3稳定性
归并排序是稳定的排序算法,因为无论是在排序拆解过程中还是在归并过程中都没有改变相同元素的相对位置,所以是稳定的。
好了,以上就是今天的全部内容了,你们学会了吗?我们下一期再见!
相关文章:

排序算法-----归并排序
目录 前言: 归并排序 1. 定义 2.算法过程讲解 2.1大致思路 2.2图解示例 拆分合成步骤 编辑 相关动态图 3.代码实现(C语言) 4.算法分析 4.1时间复杂度 4.2空间复杂度 4.3稳定性 前言: 今天我们就开始学习新的排序算法…...
docker 配置 gpu版pytorch环境--部署缺陷检测--Anomalib
目录 一、docker 配置 gpu版pyhorch环境1、显卡驱动、cuda版本、pytorch cuda版本三者对应2、拉取镜像 二、部署Anomalib1、下载Anomalib2、创建容器并且运行3、安装Anomalib进入项目路径安装依赖测试: 一、docker 配置 gpu版pyhorch环境 1、显卡驱动、cuda版本、p…...
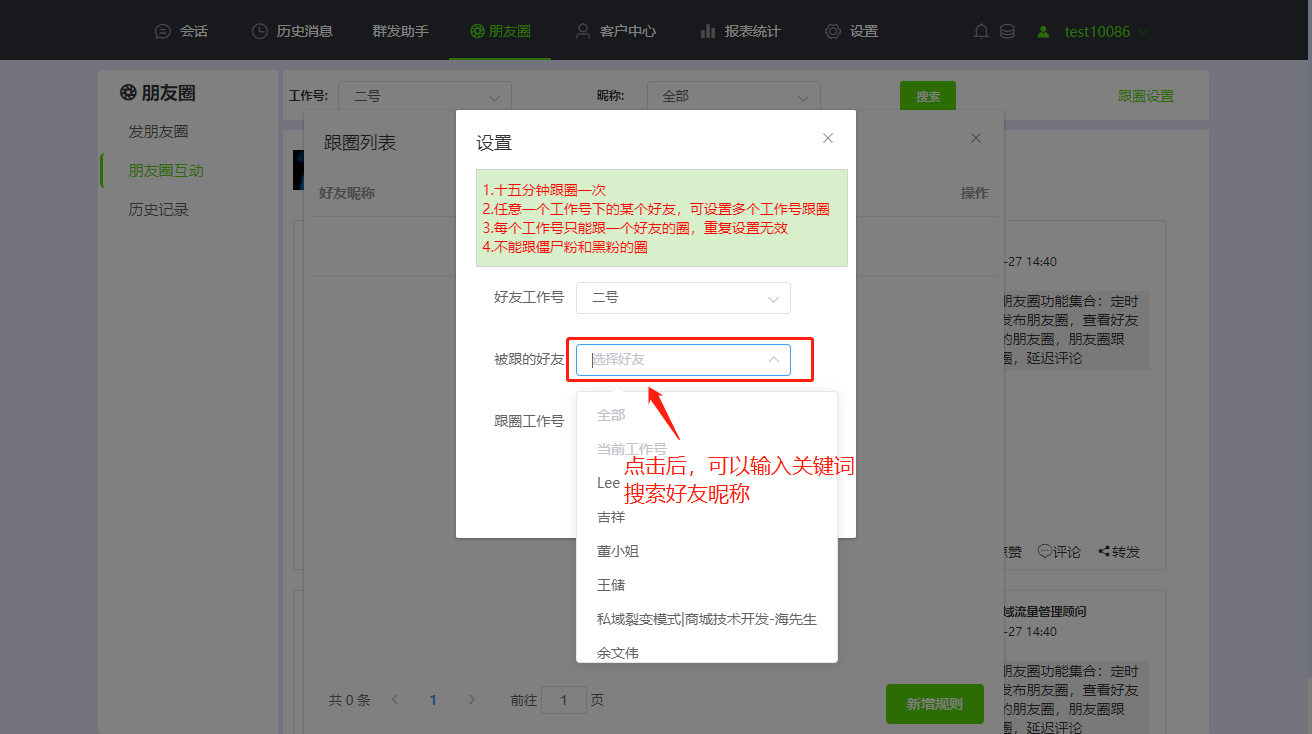
为什么定时发朋友圈会更有效呢?
这是因为在同一时段 发送的好友朋友圈 无法有效分散用户的注意力 导致曝光度难以提升 而通过推广定时发朋友圈 可根据自己的粉丝活跃度 设置发圈时间 让每一条朋友圈都能高效 传递到更多的好友手中 这样,曝光度自然而然地就大大提升了! 1.多个号…...

【跟小嘉学 PHP 程序设计】一、PHP 开发环境搭建
系列文章目录 【跟小嘉学 PHP 程序设计】一、PHP 开发环境搭建 文章目录 系列文章目录@[TOC](文章目录)前言一、PHP介绍二、Centos 安装 PHP2.1、安装并启动 Nginx2.2、安装并启动 mariadb2.3、安装 rh-php2.4、添加 Nginx 配置2.5、Nginx 服务三、使用 Docker 为 PHP 部署开发…...
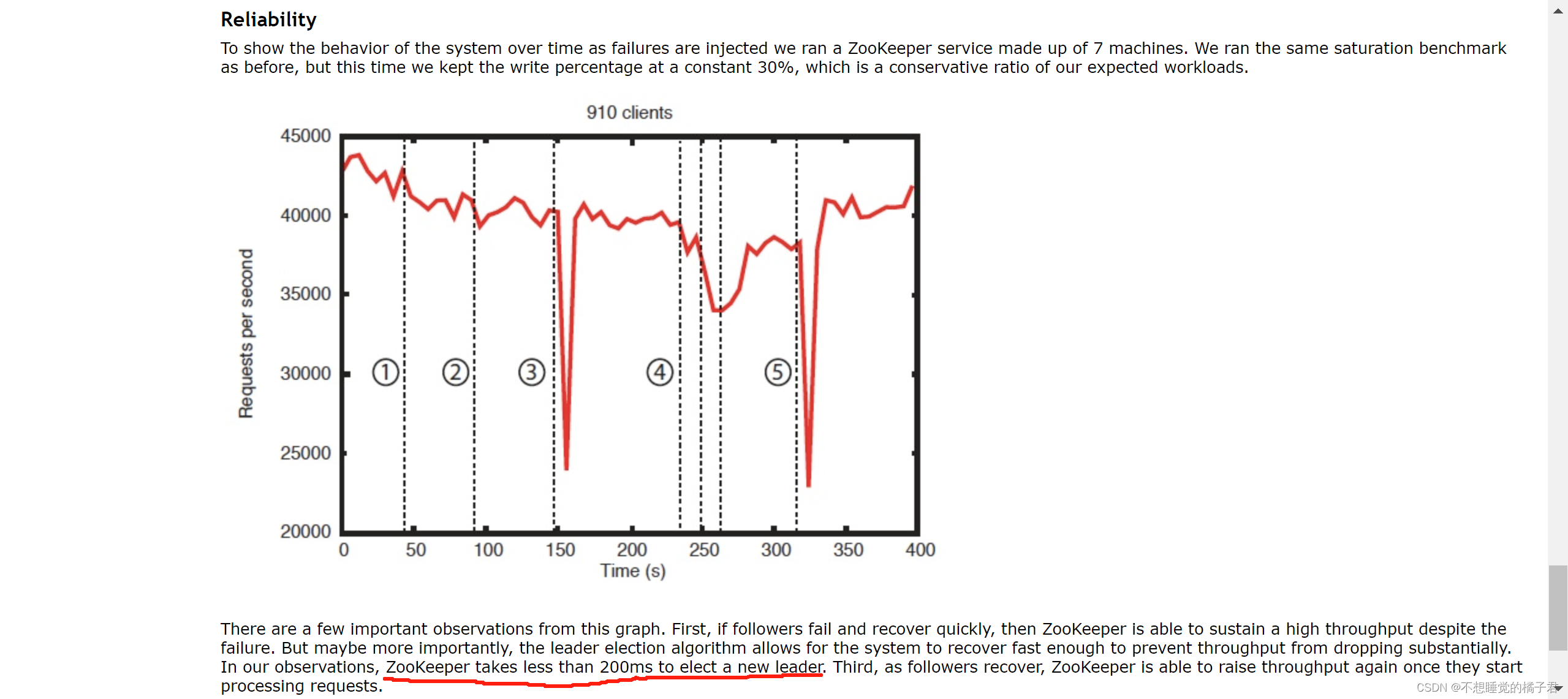
【zookeeper】zk选举、使用与三种节点简介,以及基于redis分布式锁的缺点的讨论
这里我准备了4台虚拟机,从node1到node4,其myid也从1到4. 一,zk server的启动和选举 zk需要至少启动3台Server,按照配置的myid,选举出参与选举的myid最大的server为Leader。(与redis的master、slave不同&a…...
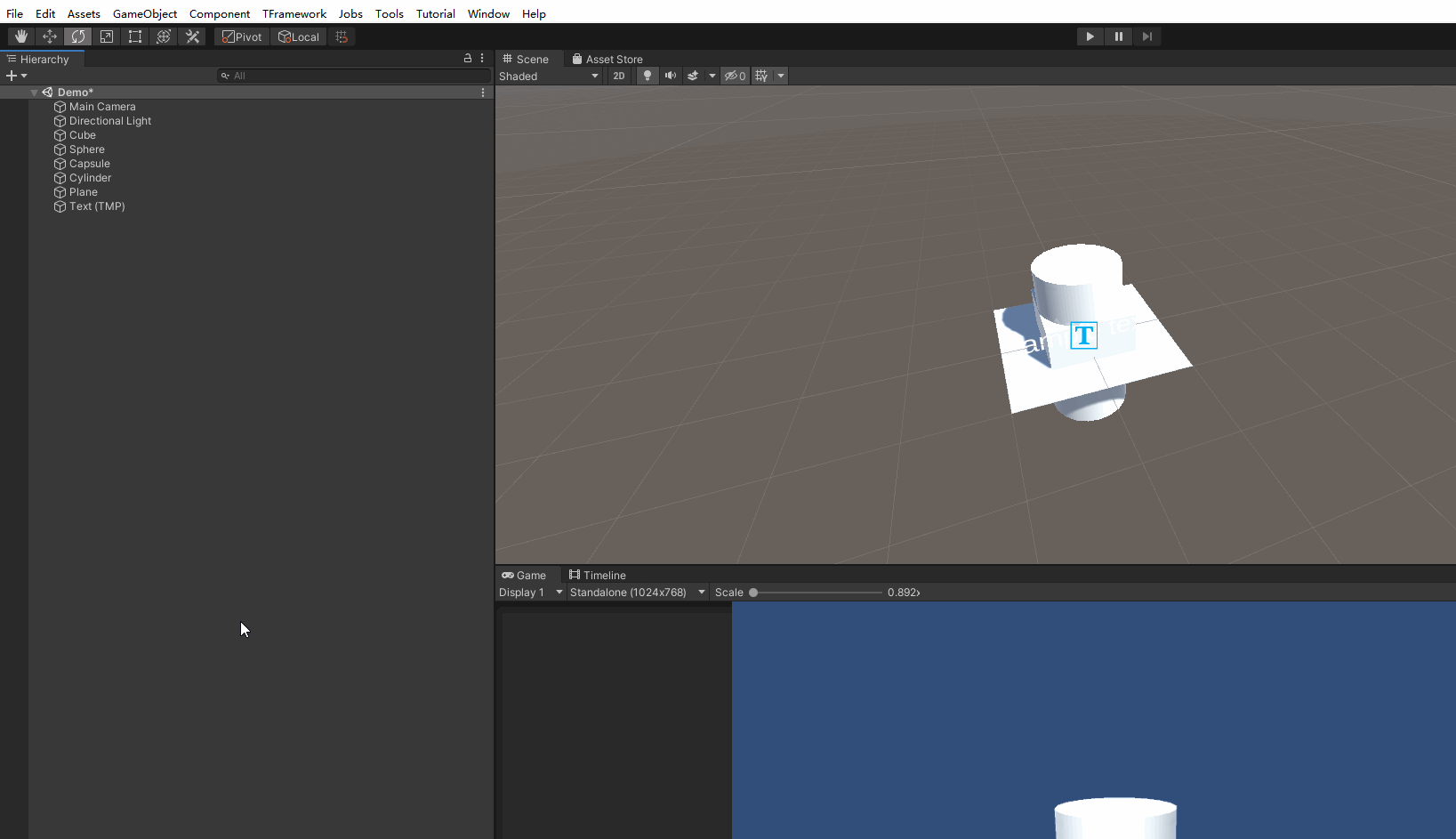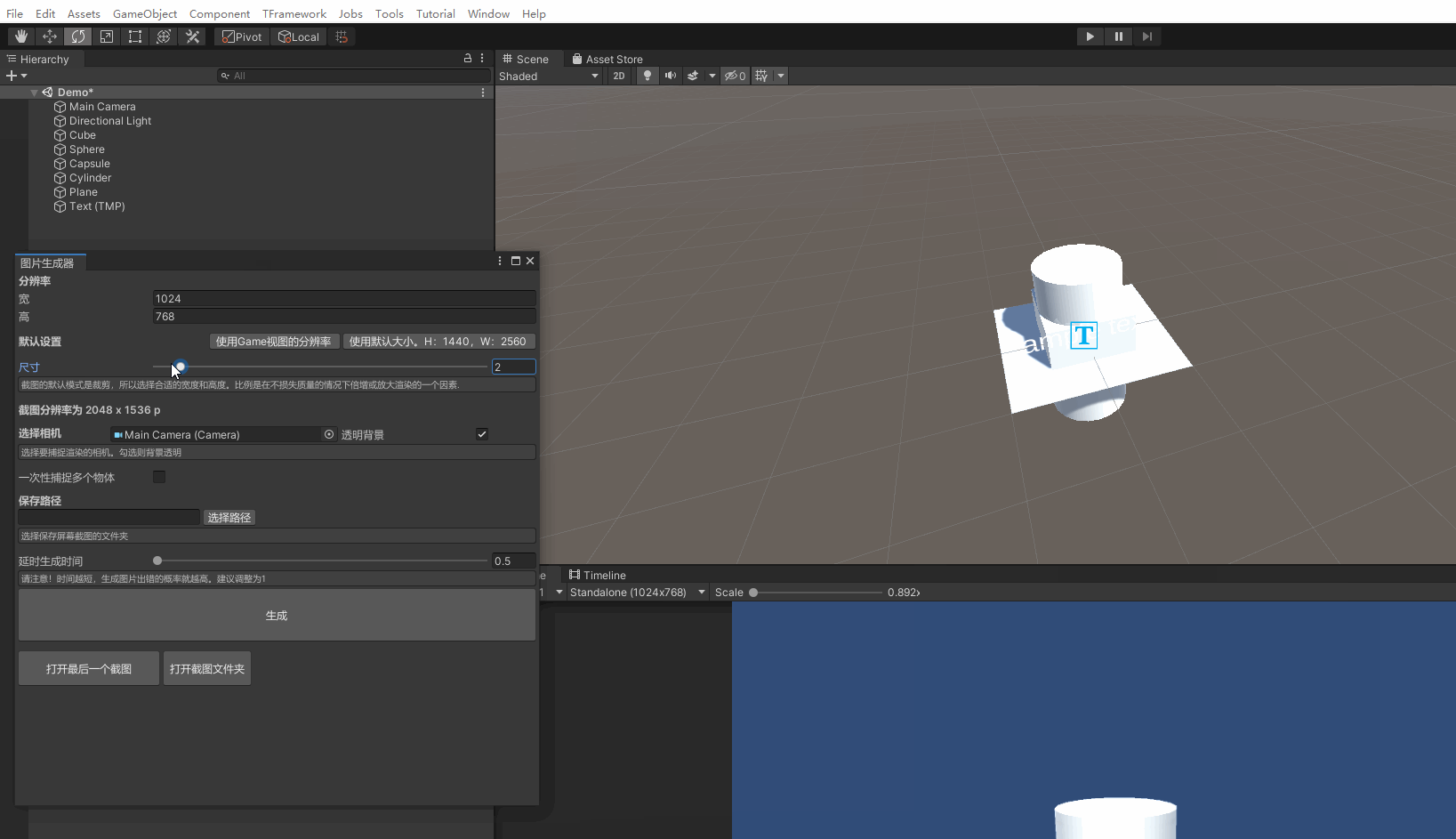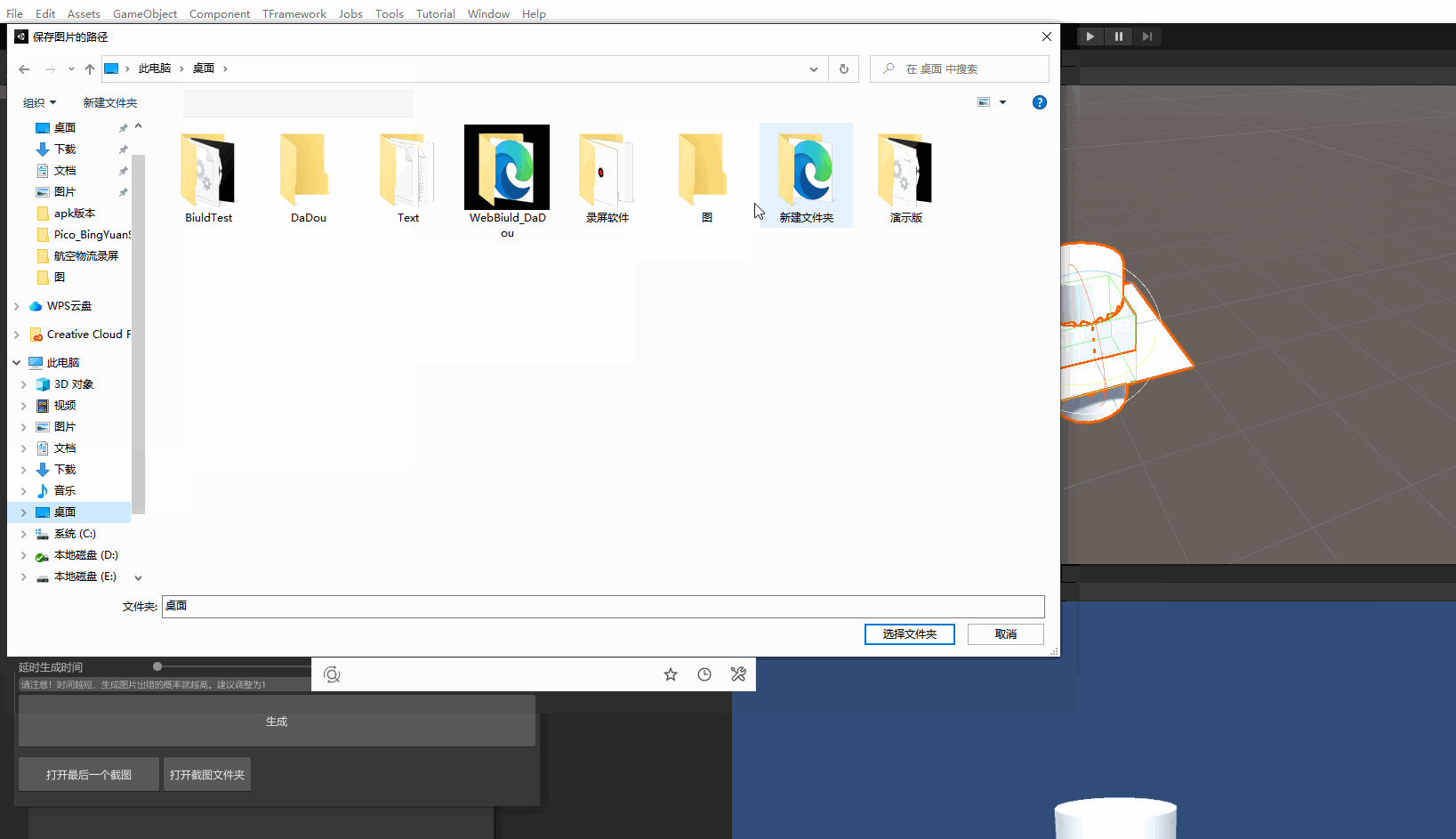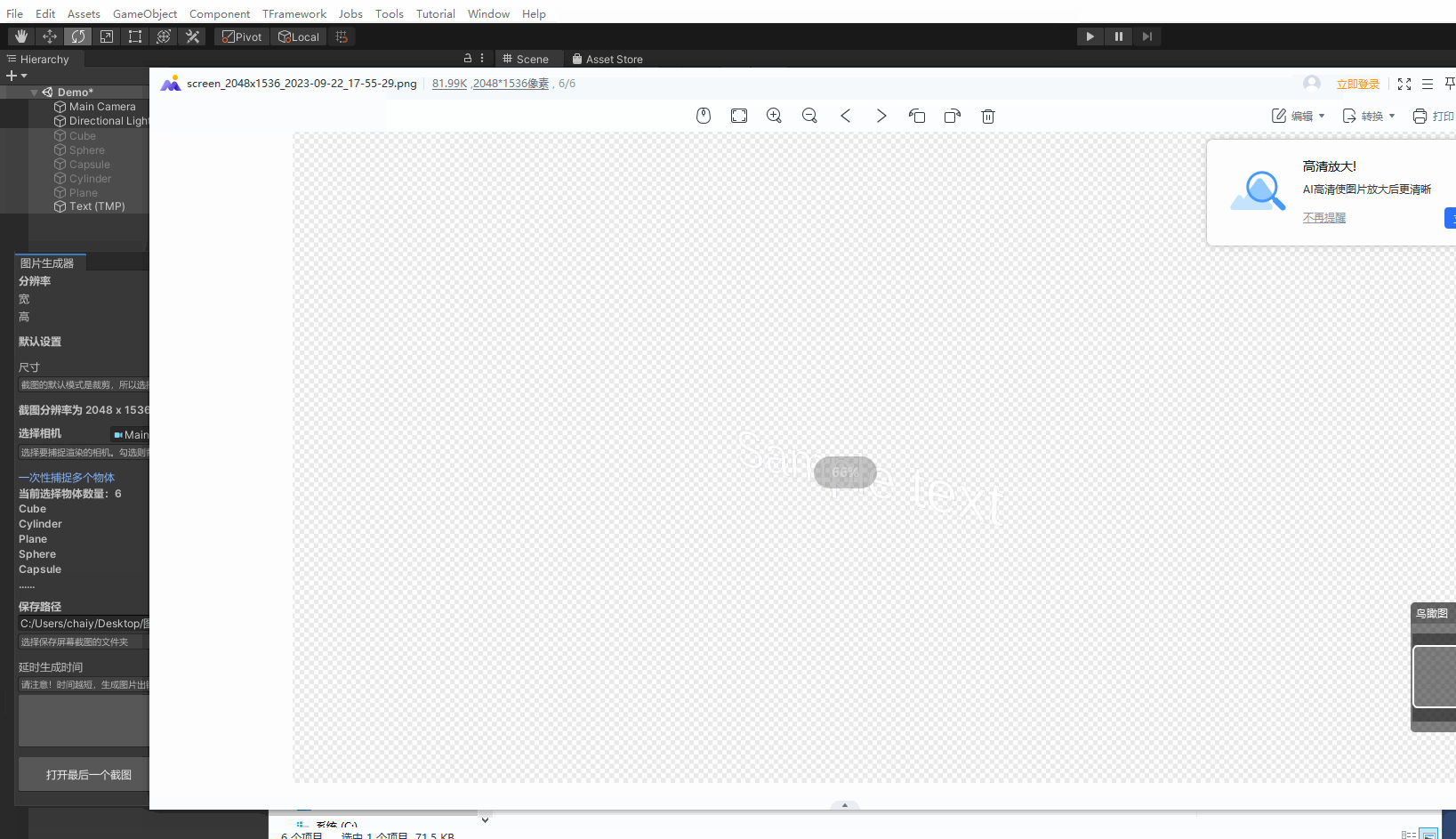
Unity截图生成图片 图片生成器 一键生成图片
使用Unity编辑器扩展技术实现快速截图功能 效果: 里面没有什么太难的技术,直接上源码吧 注意!代码需要放在Editor文件下才能正常运行 using System; using UnityEditor; using UnityEngine;[ExecuteInEditMode] public class Screenshot …...

Matlab图像处理-区域特征
凹凸性 设P是图像子集S中的点,若通过的每条直线只与S相交一次,则称S为发自P的星形,也就是站在P点能看到S的所有点。 满足下列条件之一,称此为凸状的: 1.从S中每点看,S都是星形的; 2.对S中任…...
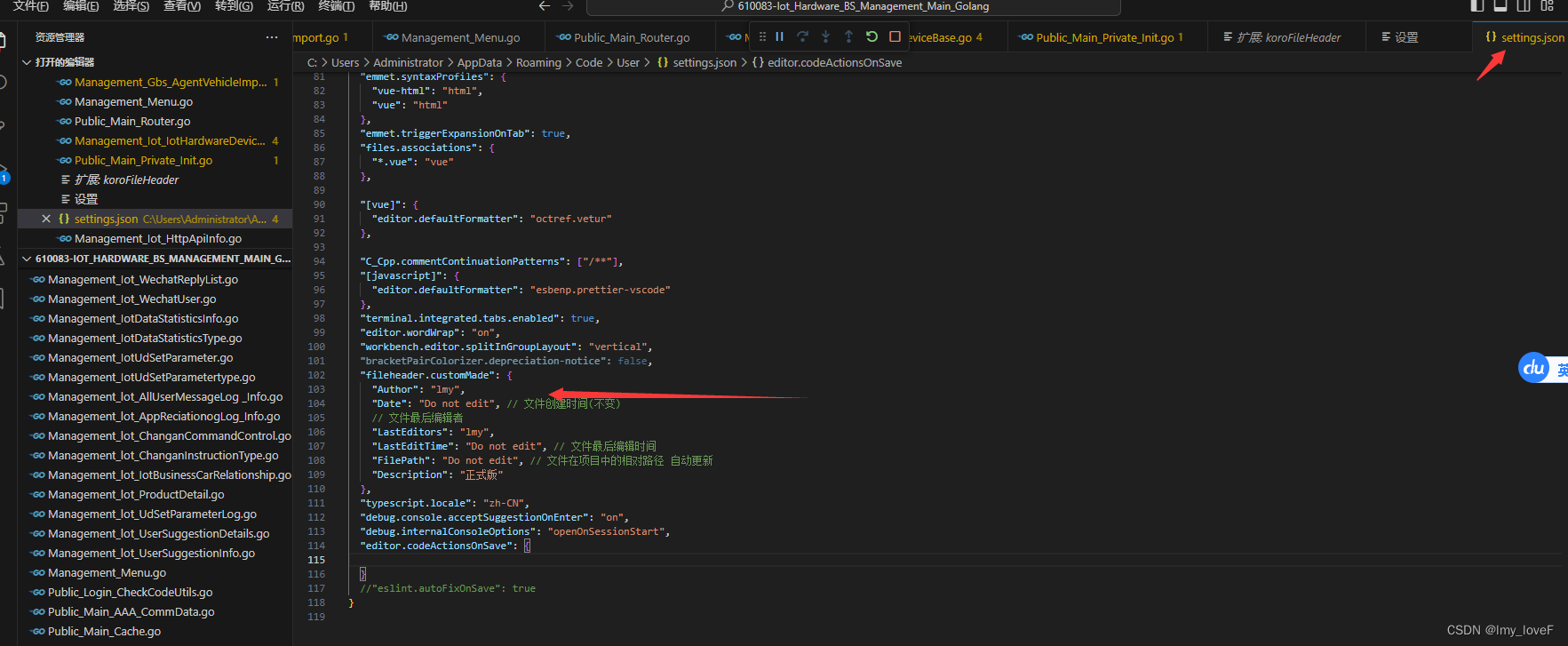
golang 自动生成文件头
安装koroFileHeader控件 打开首选项,进入设置,配置文件头信息"fileheader.customMade": {"Author": "lmy","Date": "Do not edit", // 文件创建时间(不变)// 文件最后编辑者"LastEditors"…...
Excel中的宏、VBA
一、宏是什么? EXCEL MACRO 是一种记录和播放工具,它仅记录您的 Excel 步骤,并且宏将根据需要播放任意多次。 VBA 宏可自动执行重复任务,从而节省了时间。 这是一段可在 Excel 环境中运行的编程代码,但您无需成为编码…...
2023华为杯数学建模研赛思路分享——最全版本A题深度解析
问题回顾: WLAN网络信道接入机制建模 1. 背景 无线局域网(WLAN, wireless local area network)也即Wi-Fi广泛使用,提供低成本、高吞吐和便利的无线通信服务。基本服务集(BSS, basic service set)是WLAN的…...

【校招VIP】测试方案之测试需求分析
考点介绍: 需求分析就是要弄清楚用户需要的是什么功能,用户会怎样使用系统。这样我们测试的时候才能更加清楚的知道系统该怎么样运行,才能更好的设计测试用例,才能更好的测试。 测试方案之测试需求分析-相关题目及解析内容可点击…...

滚珠螺母的清洁方式
滚珠螺母是一种通过滚珠与螺杆进行螺旋运动转换的机械零件,主要用于控制螺杆的运动轨迹和方向,把原来的滑动摩擦利用滚珠的滚动变成滚动摩擦,因此滚珠螺母的摩擦系数大大降低,从而提高了传动效率,要想滚珠螺母达到预期…...

leetcode做题笔记148. 排序链表
给你链表的头结点 head ,请将其按 升序 排列并返回 排序后的链表 。 思路一:归并排序 c语言解法 struct ListNode* merge(struct ListNode* head1, struct ListNode* head2) {struct ListNode* dummyHead malloc(sizeof(struct ListNode));dummyHead…...

多线程学习
并发:交替运行 并行:一起运行 多线程实现方式 继承Thread类 ①自己定义一个类继承Thread public class MyThread extends Thread{public void run(){}} ②重写run方法 public class MyThread extends Thread{public void run(){"重写的内容&…...

软件测试/测试开发丨ChatGPT在测试计划中的应用策略
点此获取更多相关资料 简介 测试计划是指描述了要进行的测试活动的范围、方法、资源和进度的文档。它主要包括测试项、被测特性、测试任务和风险控制等。 所以在使用ChatGPT输出结果之前,我们需要先将文档的内容框架梳理好,以及将内容范围划定好&…...
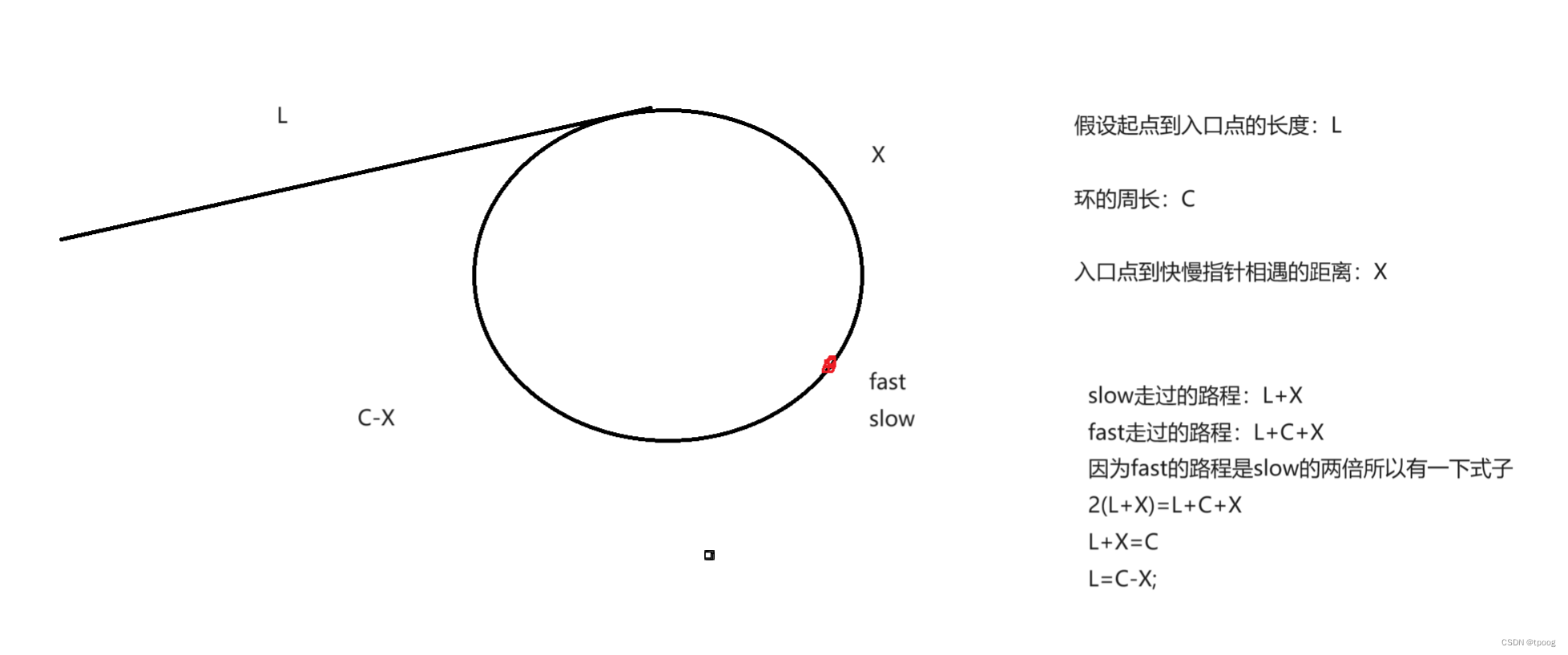
链表oj3(Leetcode)——相交链表;环形链表
一,相交链表 相交链表(Leetcode) 1.1分析 看到这个我们首先想到的就是一个一个比较他们的值有相等的就是交点,但是如果a1和b2的值就相等呢?所以这个思路不行,第二种就是依次比较链表,但是这…...

nginx反向代理
nginx反向代理8.反向代理8.1 实现http反向代理8.1.1 反向代理配置参数8.1.2 反向代理单台web服务器8.1.2.1 端口号后加"/"8.1.2.2 端口号后不加"/" 8.1.3指定location 实现反向代理,动静分离8.1.4 反向代理实例:缓存功能8.1.4.1 举例 8.1.5 实现…...
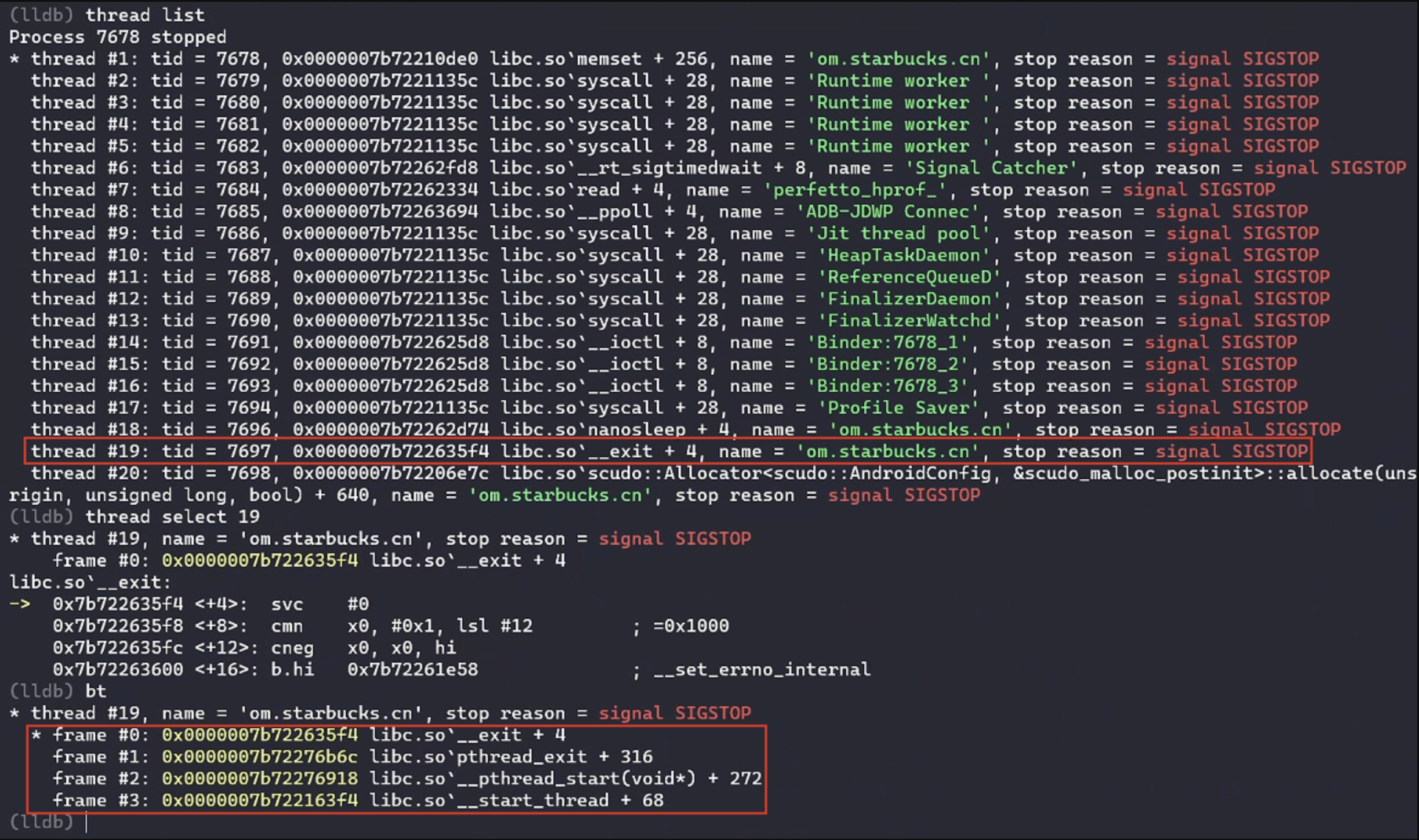
基于eBPF的安卓逆向辅助工具——stackplz
前言 stackplz是一款基于eBPF技术实现的追踪工具,目的是辅助安卓native逆向,仅支持64位进程,主要功能如下: hardware breakpoint 基于pref_event实现的硬件断点功能,在断点处可读取寄存器信息,不会被用户…...
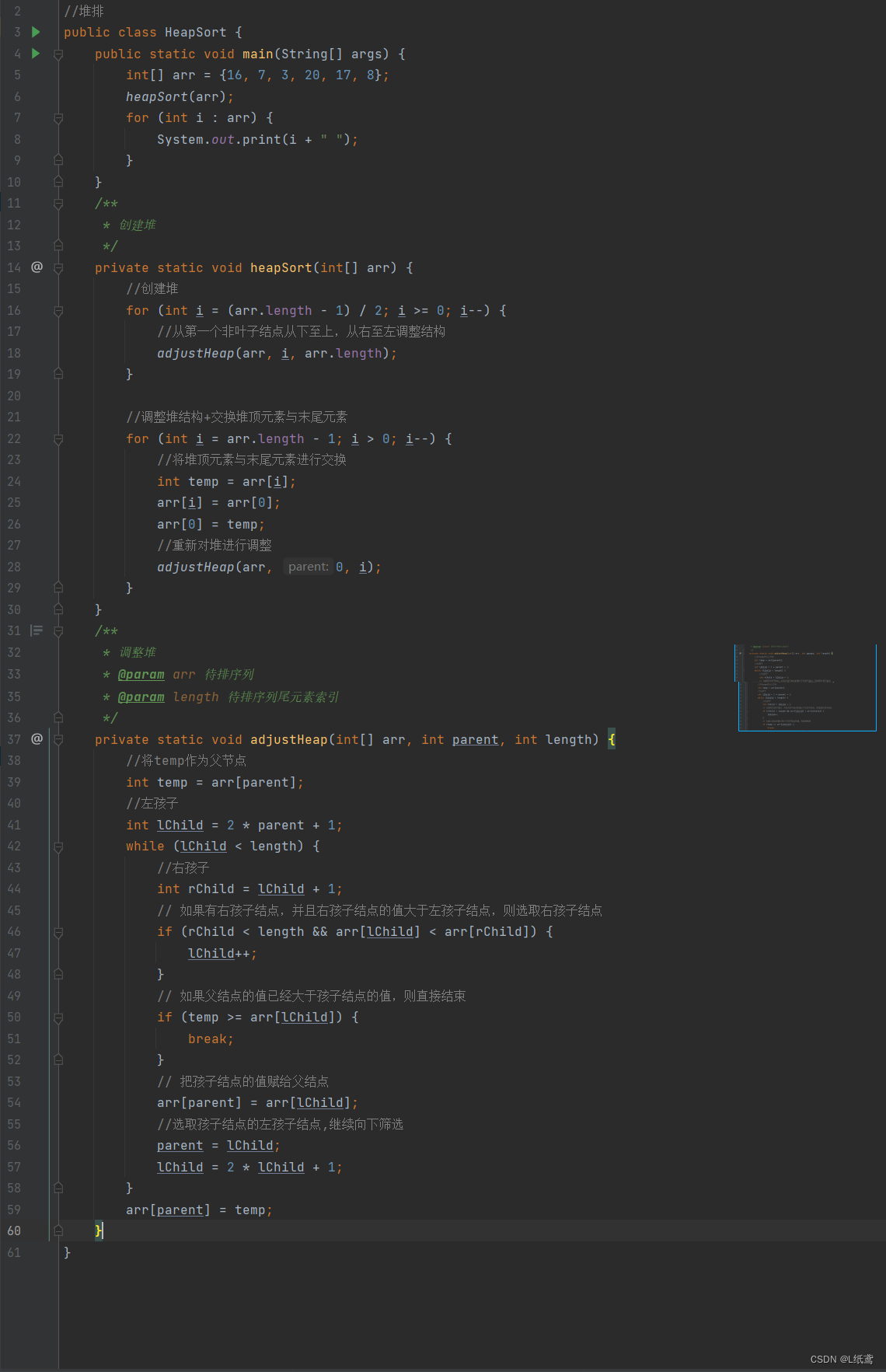
十大排序——4.堆排序
前面我们讲了堆,现在我们来看一下队排序。 堆排序的步骤: 首先将一个无序数组建立成一个大顶堆然后,将堆顶的元素和堆低的元素进行交换(即将最大的元素交换的到堆底),缩小并下潜调整堆重复上一步…...
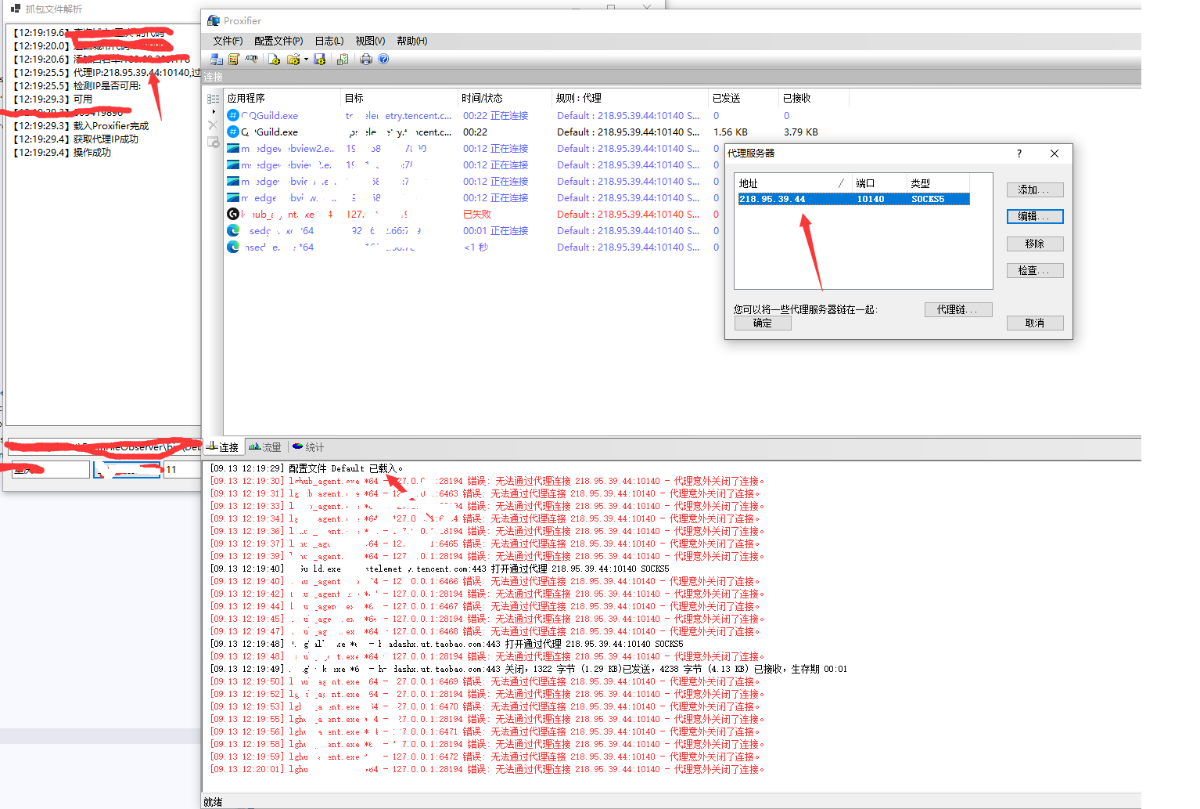
独辟蹊径”之动态切换进程代理IP
前言 项目中遇到这样一个需求,需要动态切换指定进程Sockets5代理IP,目前了解到可通过编写驱动拦截或者劫持LSP实现,LSP劫持不太稳定,驱动无疑是相对较好的解决方案,奈何水平不足便有了这"蹊径"。 初步尝试…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...

