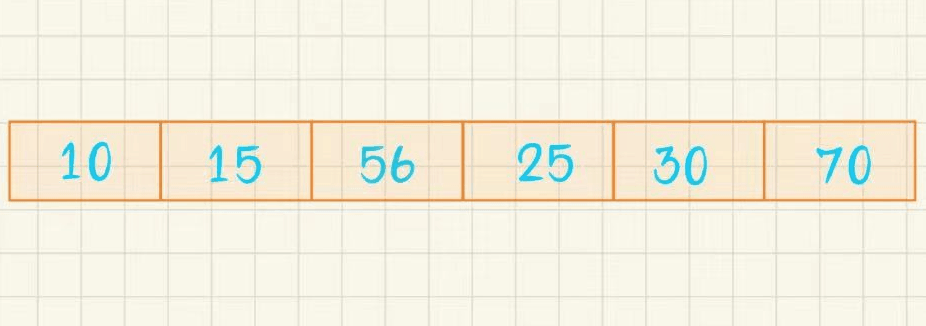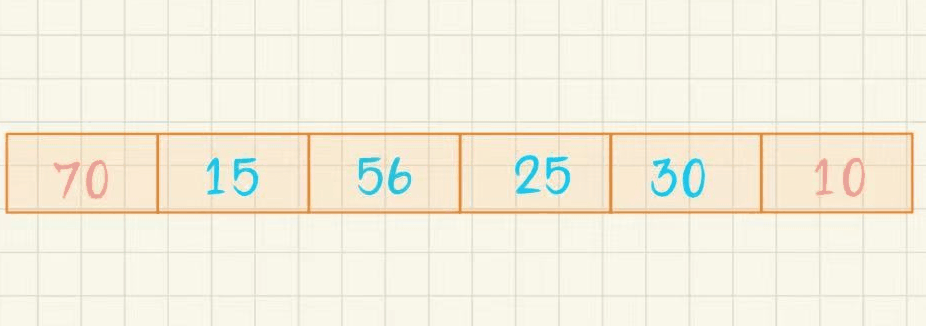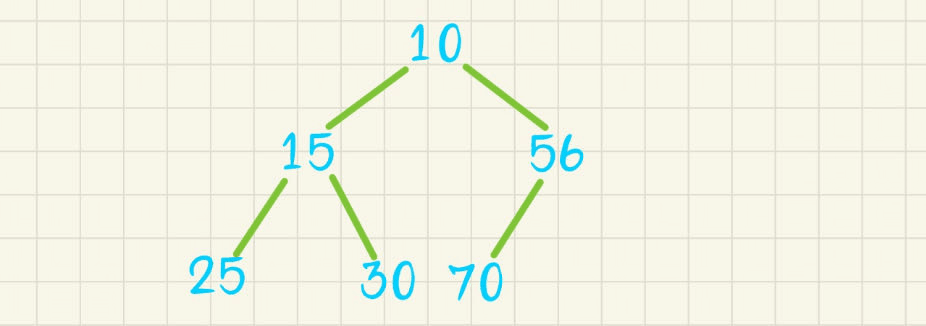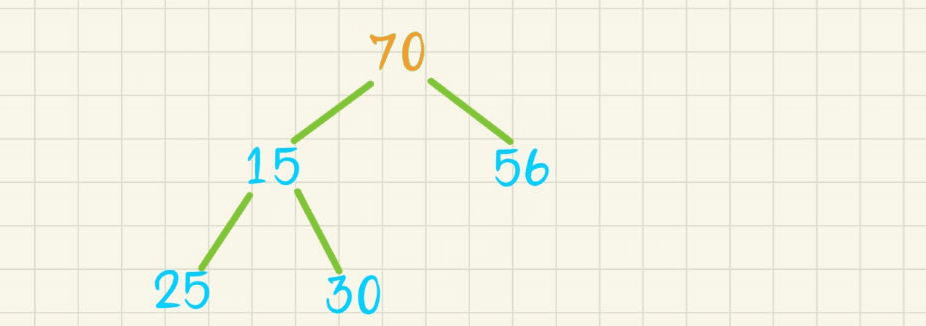
【数据结构】二叉树之堆的实现

🔥博客主页:小王又困了
📚系列专栏:数据结构
🌟人之为学,不日近则日退
❤️感谢大家点赞👍收藏⭐评论✍️
目录
一、二叉树的顺序结构
📒1.1顺序存储
📒1.2堆的性质
📒1.3堆的分类
二、堆的实现
📒2.1堆的创建
📒2.2堆的初始化
📒2.3堆的插入
📒2.4向上调整数据
📒2.5堆的删除
📒2.6向下调整数据
📒2.7堆的销毁
🗒️前言:
在上一期的文章中我们学习了一些二叉树的知识,也了解了堆的概念。堆是一颗完全二叉树,分为大堆和小堆,今天我们将实现堆的各种功能。
一、二叉树的顺序结构
📒1.1顺序存储
顺序结构存储就是使用数组来存储,一般使用数组只适合表示完全二叉树,因为不是完全二叉树会有空间的浪费。而现实使用中只有堆才会使用数组来存储。二叉树顺序存储在物理上是一个数组,在逻辑上是一颗二叉树。
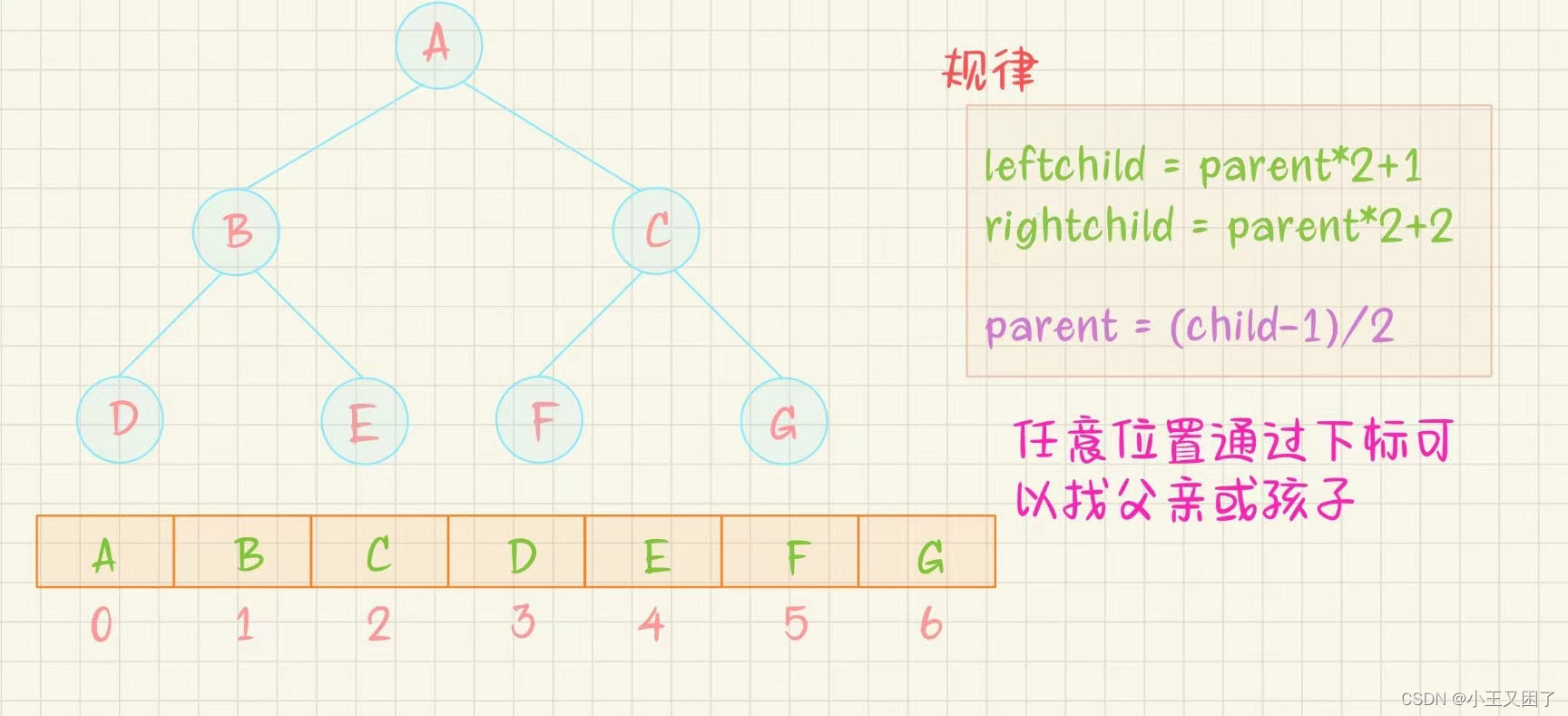
📒1.2堆的性质
- 堆中某个节点的之总是不大于或不小于其父亲节点的值
- 堆是一颗完全二叉树
📒1.3堆的分类
- 小堆:树中任意一个父亲都小于等于孩子
- 大堆:树中任意一个父亲都大于等于孩子
二、堆的实现
📒2.1堆的创建
堆的逻辑结构是树形结构,是我们想象出来的,实际上我们操作的数组,所以堆的创建和顺序表的结构相同。
typedef int HPDateType; typedef struct Heap {HPDateType* a;int size;int capacity; }HP;
📒2.2堆的初始化
我们有两种初始化的方式,一种是在初始化阶段不开辟空间,在插入过程中进行扩容;另一种是在初始化阶段就开辟空间。
void HeapInit(HP* php) {assert(php);php->a = NULL;php->size = 0;php->capacity = 0; }void HeapInit(HP* php) {assert(php); php->size = 0;php->capacity = 5;php->a = (HPDateType*)malloc(sizeof(HPDateType) * capacity);if (tmp == NULL){perror("malloc");exit(-1);} }
📒2.3堆的插入
堆是使用顺序结构的数组来存储的,我们使用尾插插入数据更方便,然后将数据调整到合适的位置。
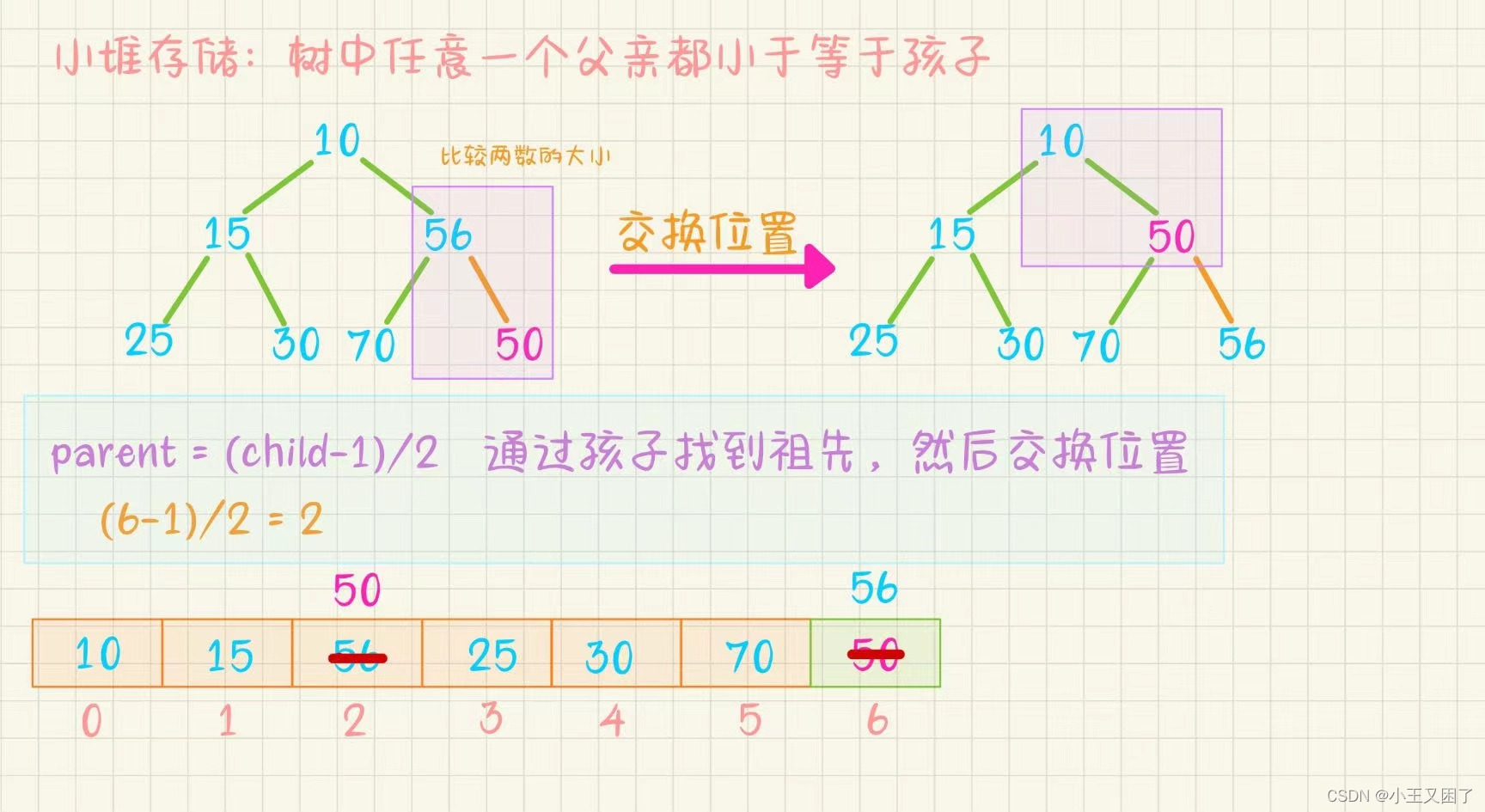
void HeapPush(HP* php, HPDataType x) {assert(php);// 扩容if (php->size == php->capacity){int newCapacity = php->capacity == 0 ? 4 : php->capacity * 2;HPDataType* tmp = (HPDataType*)realloc(php->a, sizeof(HPDataType) * newCapacity);if (tmp == NULL){perror("realloc fail");exit(-1);}php->a = tmp;php->capacity = newCapacity;}php->a[php->size] = x;php->size++;AdjustUp(php->a, php->size - 1); }如图:在小堆中插入50,50比它的父亲小,所以要交换两数的位置。我们知道孩子的下标通过 parent=(child-1)/2 就可以得到父亲的下标,然后交换两数。
📒2.4向上调整数据
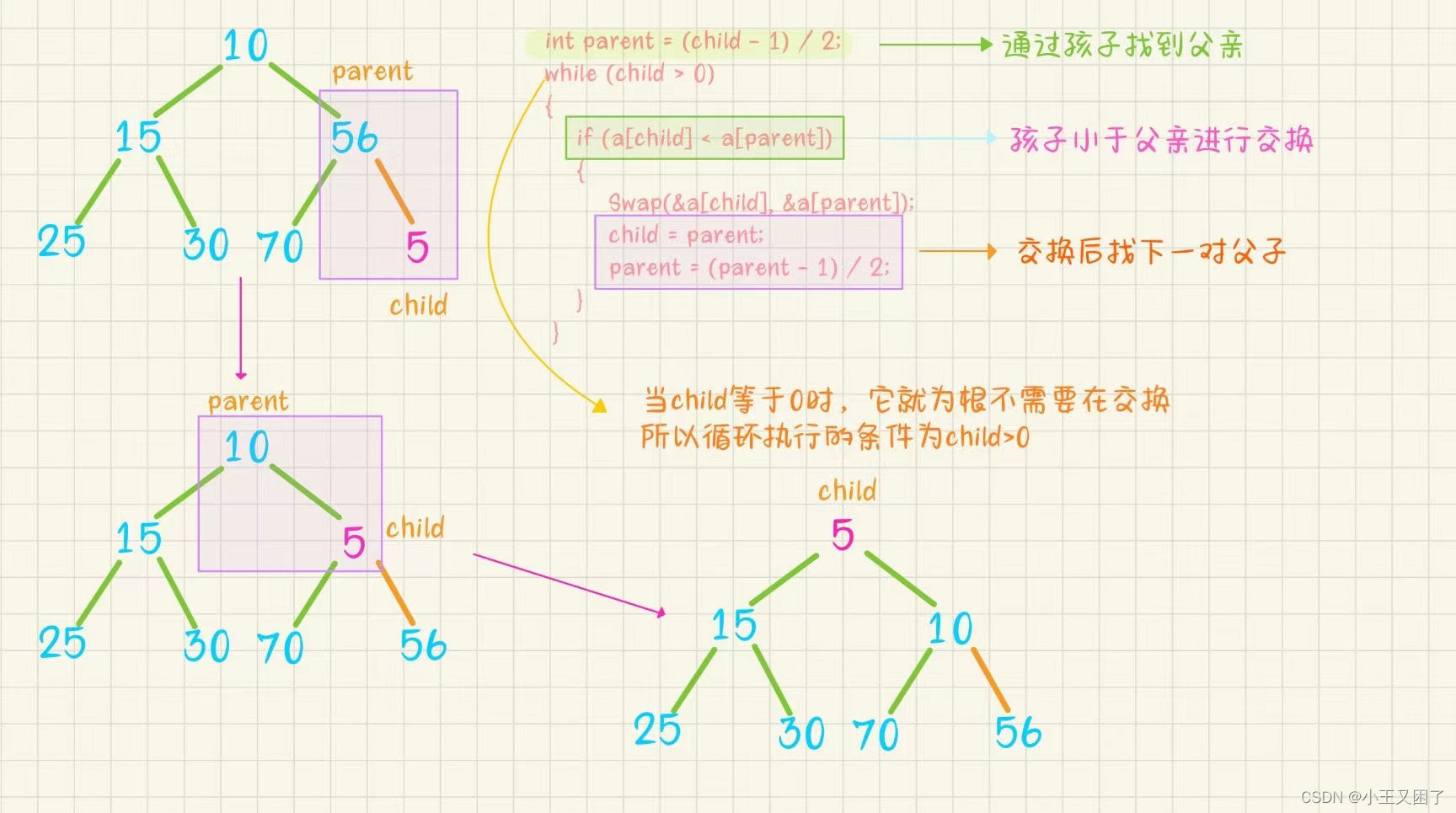
如果是小堆存储我们通过孩子的下标找到父亲,比较两数如果孩子小于父亲就交换,然后在向上比较,如果孩子不小于父亲就跳出循环。
void Swap(HPDataType* p1, HPDataType* p2) {HPDataType tmp = *p1;*p1 = *p2;*p2 = tmp; }void AdjustUp(HPDataType* a, int child) {int parent = (child - 1) / 2;while (child > 0){if (a[child] < a[parent]){Swap(&a[child], &a[parent]);child = parent;parent = (parent - 1) / 2;}else{break;}} }
📒2.5堆的删除
我们使用挪动覆盖的方法删除根,会使关系混乱,剩下的值不一定是堆,而且效率很低。这里提供一种更好的方法,将根和最后一个值交换,然后删除,最后调整数据。
void HeapPop(HP* php) {assert(php);assert(php->size > 0);Swap(&php->a[0], &php->a[php->size - 1]);--php->size;AdjustDown(php->a, php->size, 0); }这里要注意有数据的时候才能删除,所以要加入 assert(php->size > 0) 进行判断。
📒2.6向下调整数据
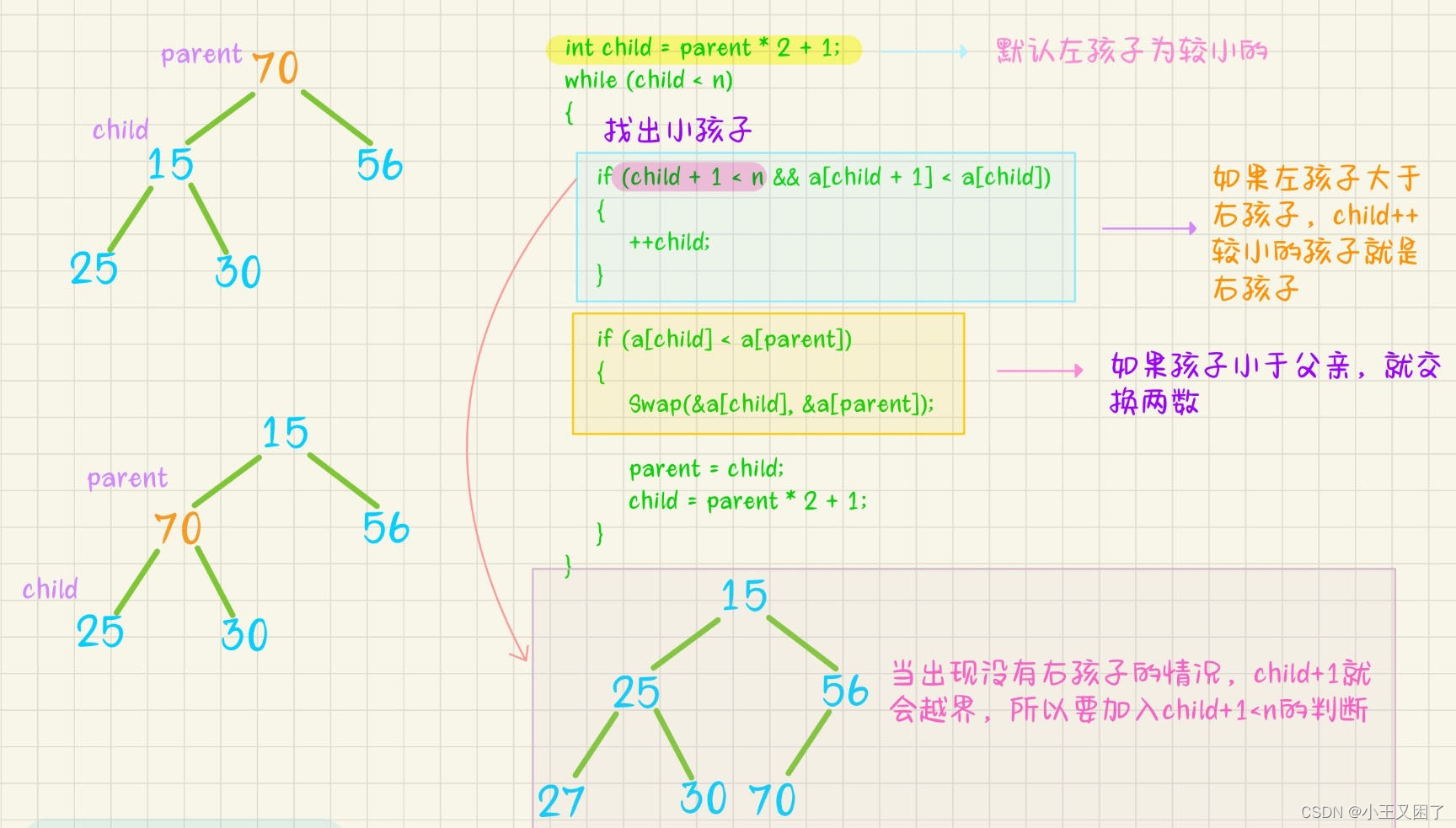
如果是小堆存储我们要找到左右孩子中较小的数,然后与父亲交换,再找到下一层重复步骤,直到找到叶节点结束。
void AdjustDown(HPDataType* a, int n, int parent) {//默认左孩子是较小的int child = parent * 2 + 1;while (child < n){// 找出小的那个孩子if (child + 1 < n && a[child + 1] < a[child]){++child;}if (a[child] < a[parent]){Swap(&a[child], &a[parent]);// 继续往下调整parent = child;child = parent * 2 + 1;}else{break;}} }
📒2.7堆的销毁
我们使用动态开辟内存,要及时释放空间并置为空指针,不然会造成数据泄露。
void HeapDestroy(HP* php) {assert(php);free(php->a);php->a = NULL;php->size = php->capacity = 0; }
本次的内容到这里就结束啦。希望大家阅读完可以有所收获,同时也感谢各位读者三连支持。文章有问题可以在评论区留言,博主一定认真认真修改,以后写出更好的文章。你们的支持就是博主最大的动力。
相关文章:
【数据结构】二叉树之堆的实现
🔥博客主页:小王又困了 📚系列专栏:数据结构 🌟人之为学,不日近则日退 ❤️感谢大家点赞👍收藏⭐评论✍️ 目录 一、二叉树的顺序结构 📒1.1顺序存储 📒1.2堆的性质…...
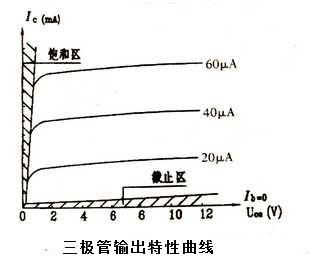
电工-三极管输入输出特性曲线讲解
三极管特性曲线是反映三极管各电极电压和电流之间相互关系的曲线,是用来描述晶体三极管工作特性曲线,常用的特性曲线有输入特性曲线和输出特性曲线。这里以下图所示的共发射极电路来分析三极管的特性曲线。 输入特性曲线 该曲线表示当e极与c极之间的电…...
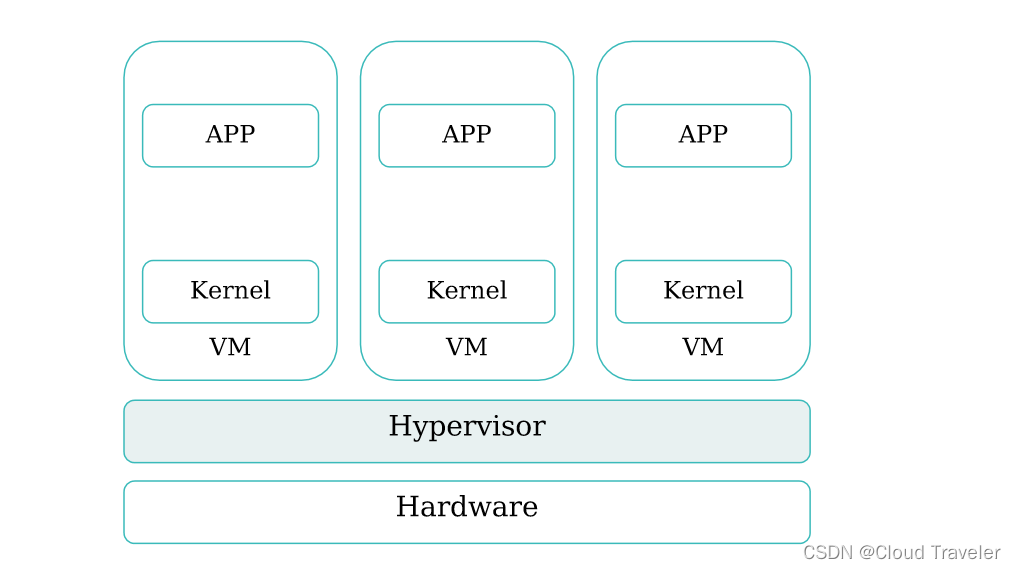
深入解析容器与虚拟化:技术、对比与生态
深入解析容器与虚拟化:技术、对比与生态 文章目录 深入解析容器与虚拟化:技术、对比与生态容器和虚拟化的基本概念和原理容器的定义和特点虚拟化的定义和特点 容器使用场景容器和虚拟机的对比虚拟化技术的四个特点容器实现虚拟化的原理常见容器引擎和容器…...

制作游戏demo的心得
制作这个游戏demo出来的心得 https://www.bilibili.com/video/BV1cF411m7Dh/ 制作游戏demo的心得 制作游戏demo,主要是为了表现自己的技术,那就一门心思想着如何提高表现力就行了,在整体的画面渲染风格方面或许没有什么可选择的,…...
Web Tour Server窗口闪现
1.打开该文件所在位置 2.右击选择编辑,在最后一行加上pause,保存后重新打开Server窗口 3.重新打开后,若出现以下情况: 以管理员身份打开cmd命令行,输入命令netstat -aon|findstr “1080”,查看1080端口占用…...

Linux下的基本指令
目录 01. ls 指令 02. pwd命令 03. cd 指令 04. touch指令 05.mkdir指令(重要): 06.rmdir指令 && rm 指令(重要): 07.man指令(重要): 08mv指令ÿ…...

随机数生成器代码HTML5
代码如下 <!DOCTYPE html> <html> <head> <title>随机数生成器</title> <meta name"viewport" content"widthdevice-width, initial-scale1.0"> <style> body { text-align: center; bac…...
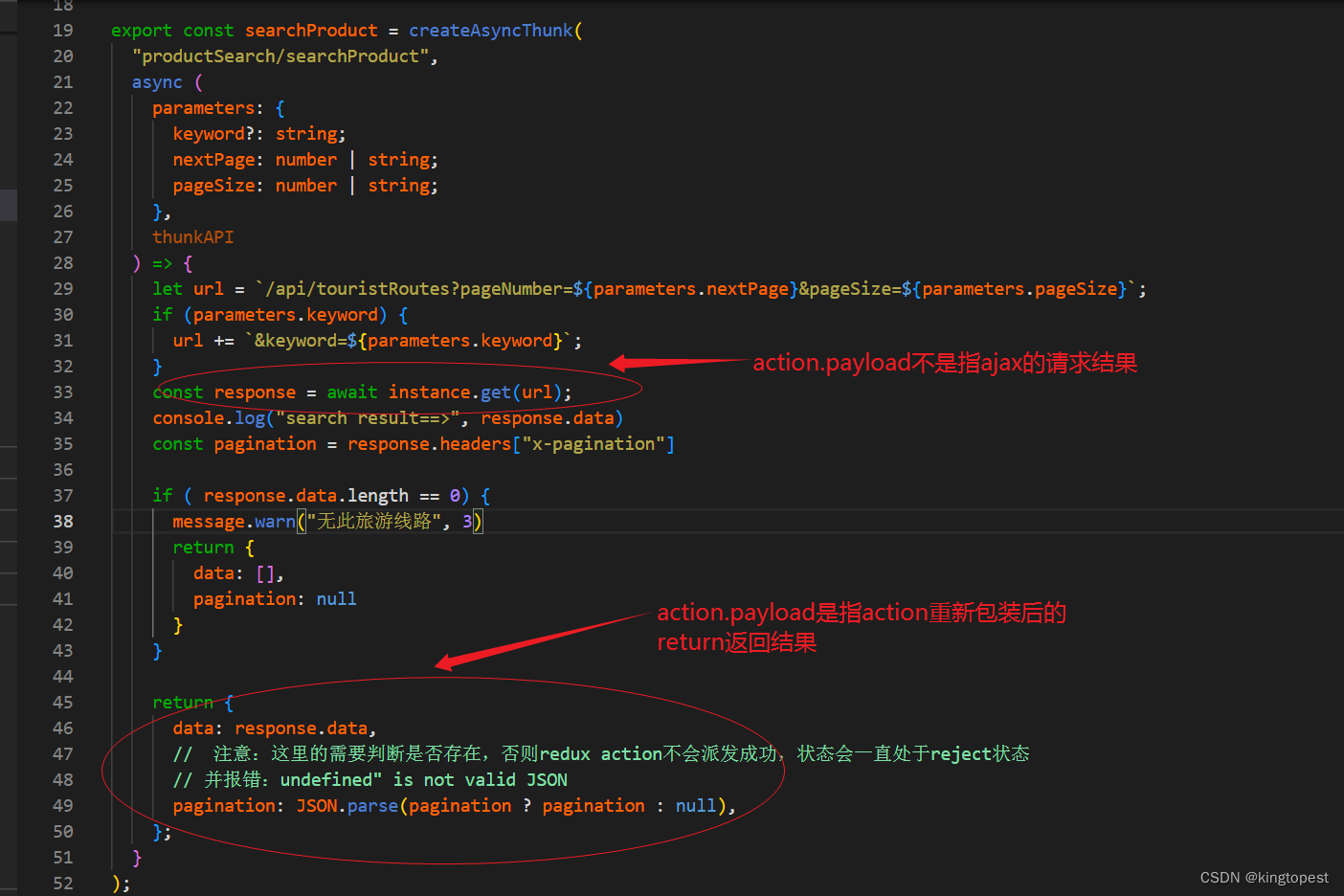
正确理解redux Toolkits中createSlice的action.payload
使用redux Toolkits中的createSlice编写extraReducers经常看到使用action.payload来更新state状态值: 那么action.payload指的到底是什么? 让我们看看action的定义部分: 注意: action.payload不是上面ajax请求的返回内容&#x…...
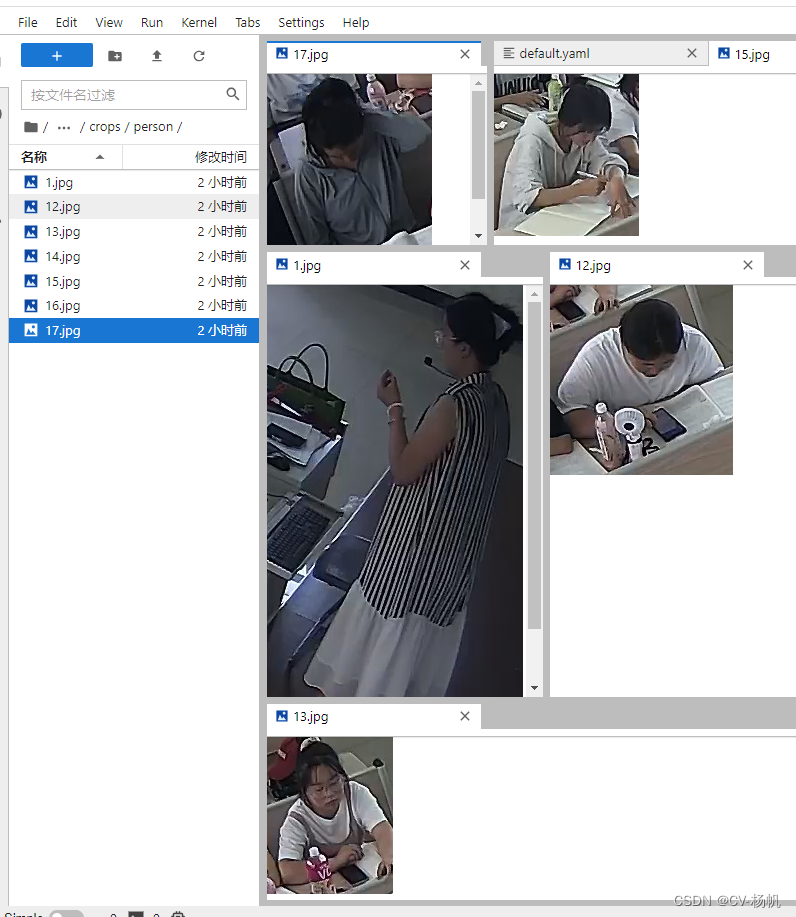
YOLOv8快速复现 官网版本 ultralytics
YOLOV8环境安装教程.:https://www.bilibili.com/video/BV1dG4y1c7dH/ YOLOV8保姆级教学视频:https://www.bilibili.com/video/BV1qd4y1L7aX/ b站视频:https://www.bilibili.com/video/BV12p4y1c7UY/ 1 平台搭建YOLOv8 平台:https://www.a…...
Haproxy搭建 Web 群集实现负载均衡
目录 1 Haproxy 1.1 HAProxy的主要特性 1.2 HAProxy负载均衡策略 1.3 LVS、Nginx、HAproxy的区别 2 Haproxy搭建 Web 群集 2.1 haproxy 服务器部署 2.1.1 关闭防火墙 2.1.2 内核配置(实验环境可有可无) 2.1.3 安装 Haproxy 2.1.4 Haproxy服务…...
Tessy 5.0.4
Tessy 5.0.4 Linux 2692407267qq.com,更多内容请见http://user.qzone.qq.com/2692407267/...

mybatis-plus根据指定条件批量更新
1.service实现类中 比如我这里只针对UserEntity,在UserServiceImpl下(该实现类是继承了mybatis-plus的ServiceImpl的)新增如下代码: public boolean updateBatchByQueryWrapper(Collection<UserEntity> entityList, Funct…...

虹科方案 | LIN/CAN总线汽车零部件测试方案
文章目录 摘要一、汽车零部件测试的重要性?二、虹科的测试仿真工具如何在汽车零部件测试展露头角?三、应用场景**应用场景1:方向盘开关的功能测试****应用场景2:各类型电机的控制测试****应用场景3:RGB氛围灯的功能测试…...

[solidity]合约调用合约
先写一个简单的合约将其部署,部署后的合约地址为:0xd9145CCE52D386f254917e481eB44e9943F39138 // SPDX-License-Identifier: MIT pragma solidity ^0.8.0;contract A{string myname;function setName(string memory _name) public{myname_name;}functi…...
Vulnhub系列靶机---JANGOW 1.0.1
文章目录 网卡配置信息收集主机发现端口扫描 漏洞利用反弹Shell提权 靶机文档:JANGOW 1.0.1 下载地址:Download (Mirror) 难易程度:. 网卡配置 水果味儿 信息收集 主机发现 端口扫描 访问80端口 点击site目录 点击页面上方的一个选项&…...

肖sir__项目环境之全流程__005
一、测试流程(h模型) 1、需求文档(产品) 需求文档(软件需求规格说明书srs) (1)如何分析需求 a、显示需求(主流程、功能,业务) b、隐性需求&#x…...

搜狗输入法下键翻页
搜狗输入法下键翻页 从官网下载 搜狗输入法智慧版关闭超级候选关闭候选...

C#多线程
一、多线程实现方式 1. 使⽤Thread类: System.Threading.Thread 类是C#中最基本的多线程编程⼯具。 2. 使⽤ThreadPool: 线程池是⼀个管理和重⽤线程的机制,它可以在应⽤程序中创建和使 ⽤多个线程,⽽⽆需显式地管理线程的…...

Unity 编辑器常用方法
unity编辑器开发 脚本注解1. RuntimeInitializeOnLoadMethod2. ColorUsage3. Header4. SerializeField5. HideInInspector6. Space7. Range8. Multiline9.[RequireComponent(typeof())]10.HelpURL 右键菜单注解1. CreateAssetMenu - 针对ScriptableObject 菜单栏注解1. MenuIt…...
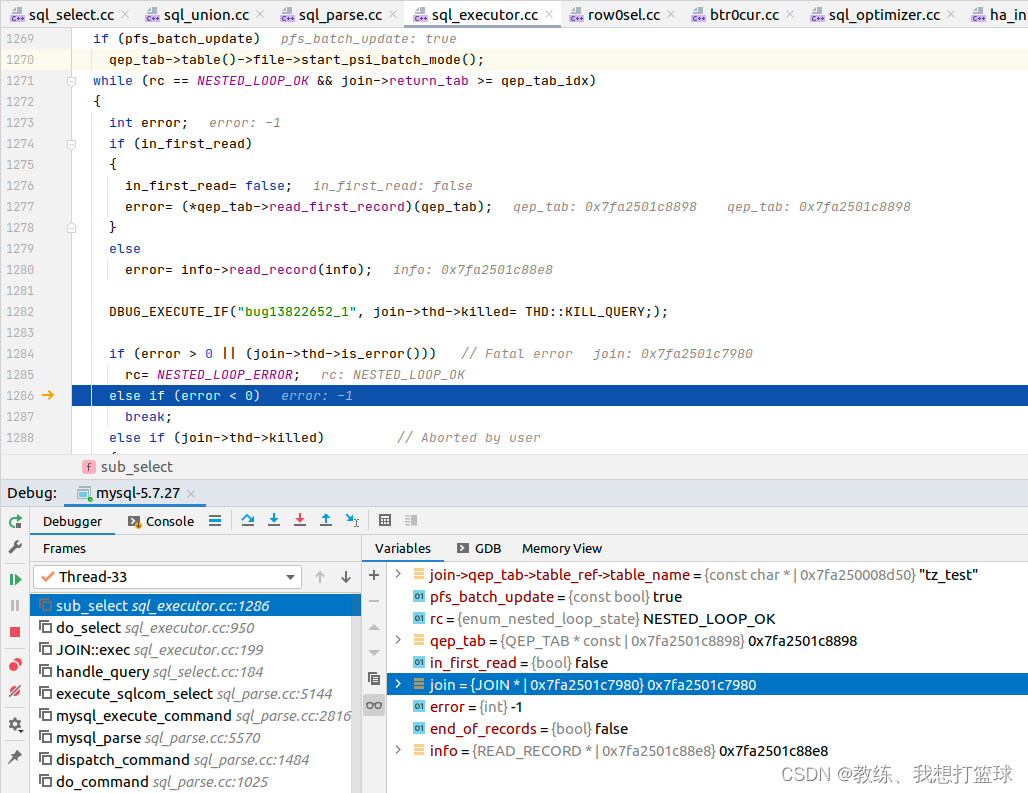
21 mysql ref 查询
前言 这里主要是 探究一下 explain $sql 中各个 type 诸如 const, ref, range, index, all 的查询的影响, 以及一个初步的效率的判断 这里会调试源码来看一下 各个类型的查询 需要 lookUp 的记录 以及 相关的差异 此系列文章建议从 mysql const 查询 开始看 测试表结构…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

怎么让Comfyui导出的图像不包含工作流信息,
为了数据安全,让Comfyui导出的图像不包含工作流信息,导出的图像就不会拖到comfyui中加载出来工作流。 ComfyUI的目录下node.py 直接移除 pnginfo(推荐) 在 save_images 方法中,删除或注释掉所有与 metadata …...

脑机新手指南(七):OpenBCI_GUI:从环境搭建到数据可视化(上)
一、OpenBCI_GUI 项目概述 (一)项目背景与目标 OpenBCI 是一个开源的脑电信号采集硬件平台,其配套的 OpenBCI_GUI 则是专为该硬件设计的图形化界面工具。对于研究人员、开发者和学生而言,首次接触 OpenBCI 设备时,往…...
)
安卓基础(Java 和 Gradle 版本)
1. 设置项目的 JDK 版本 方法1:通过 Project Structure File → Project Structure... (或按 CtrlAltShiftS) 左侧选择 SDK Location 在 Gradle Settings 部分,设置 Gradle JDK 方法2:通过 Settings File → Settings... (或 CtrlAltS)…...

小木的算法日记-多叉树的递归/层序遍历
🌲 从二叉树到森林:一文彻底搞懂多叉树遍历的艺术 🚀 引言 你好,未来的算法大神! 在数据结构的世界里,“树”无疑是最核心、最迷人的概念之一。我们中的大多数人都是从 二叉树 开始入门的,它…...

自然语言处理——文本分类
文本分类 传统机器学习方法文本表示向量空间模型 特征选择文档频率互信息信息增益(IG) 分类器设计贝叶斯理论:线性判别函数 文本分类性能评估P-R曲线ROC曲线 将文本文档或句子分类为预定义的类或类别, 有单标签多类别文本分类和多…...