[Machine Learning][Part 2]监督学习的实现
目录
线性模型实现:
cost function :代价函数或者损失函数——衡量模型优劣的一个指标
理论:
代码实现:
梯度下降——自动寻找最小的cost function 代价函数
梯度的概念:
梯度下降公式:
实现一个简单的监督学习的模型:预测part1 中提到的买房模型。
模型中有一个输入参数:房子面积 (单位:1000平方)x;一个输出结果:房子价格:y(单位:千美元)
目前假设训练数据有两个:
- 1000平方米的房子,售价300万美元
- 2000平方米的房子,售价500万美元
x_train = np.array([1.0, 2.0]) #features
y_train = np.array([300.0, 500.0]) #target value训练数据的图像是:
# 绘制训练数据
# Plot the data points
plt.scatter(x_train, y_train, marker='x', c='r')
# Set the title
plt.title("Housing Prices")
# Set the y-axis label
plt.ylabel('Price (in 1000s of dollars)')
# Set the x-axis label
plt.xlabel('Size (1000 sqft)')
plt.show()

x_train中保存的是房子面积的集合,y_train中保存的是对应面积房子的价格
线性模型实现:
首先,线性模型的计算公式是y = w*x+b,其中x是输入变量,y输出变量。可以看到模型是由w,b这两个参数来决定的。
这个数学模型可以用代码表示如下:
ef compute_model_output(x, w, b):"""Computes the prediction of a linear modelArgs:x (ndarray (m,)): Data, m examplesw,b (scalar) : model parametersReturnsy (ndarray (m,)): target values"""m = x.shape[0] #获取训练数据的数目f_wb = np.zeros(m) #将模型输出值初始化为0for i in range(m):f_wb[i] = w*x[i]+breturn f_wb上述代码中x表示输入的房子面积,w和b表示的模型的参数。
然后,我们先给w,b赋值来调用一下这个模型并绘制出模型图形:w=100,b=100
w= 100
b = 100
tmp_f_wb = compute_model_output(x_train,w,b)# Plot our model prediction
plt.plot(x_train,tmp_f_wb,c = 'b',label='Our Prediction')
# Plot the data points
plt.scatter(x_train,y_train,marker='x',c='r',label = 'Actual Value')# draw picture of module
# Set the title
plt.title("Housing Prices")
# Set the y-axis label
plt.ylabel('Price (in 1000s of dollars)')
# Set the x-axis label
plt.xlabel('Size (1000 sqft)')
plt.legend()
plt.show()输出如下:

可以看到当前的w,b实现的模型与实际值差距很大,那么如何找到合适的w,b呢,这就需要引入衡量模型准确度的一个指标cost function,被翻译成代价函数或者损失函数。
cost function :代价函数或者损失函数——衡量模型优劣的一个指标
理论:
我们的目标是为了寻找一个合适的model,可以给出精确的房价预测。代价函数用来衡量当前模型的优劣,通过观察这个指标可以帮我们找到最佳模型。代价函数的一种方式是通过当前预测值和实际值之间的方差来实现,因此当代价函数为0或者无限趋近于0时,模型的精确度是最高的。实现公式如下:

公式(2)表示我们的预测模型计算出来的第i的训练数据的结果。
公式(1)代价函数J(w,b)等于所有训练数据的代价函数的期望的二分之一
代码实现:
# 计算代价函数
def compute_cost(x, y, w, b):"""Computes the cost function for linear regression.Args:x (ndarray (m,)): Data, m examplesy (ndarray (m,)): target valuesw,b (scalar) : model parametersReturnstotal_cost (float): The cost of using w,b as the parameters for linear regressionto fit the data points in x and y"""# number of training examplesm = x.shape[0]cost_sum = 0for i in range(m):f_wb = w*x[i]+bcost = (f_wb-y[i])**2cost_sum = cost_sum+costtotal_cost = (1/(2*m))*cost_sumreturn total_cost上面代码的total_cost 就是公式(1)的实现结果。
现在假设b=100为固定值,来看一下代价函数和模型精确度的关系:
w=160, 可以看到左图为预测模型,右图为当前w,b组合的情况下的模型的代价函数还没有到达最小值,所以左图中的蓝色预测模型与实际数据的红点并没有重合
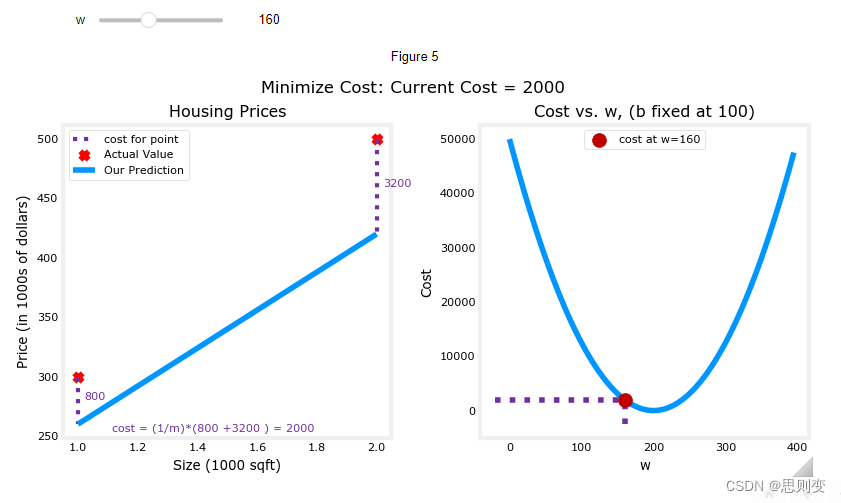
w=200,可以看到右图中此时的cost代价函数最小,左图中的实际数据点也与预测模型完全重合

通过上面的对比可以发现通过cost function J(w,b)可以找到最佳的模型参数。因为上面的例子中只有两个训练数据,当有多个训练数据时,所有的训练数据不一定会全落在同一条直线上,这种情况下我们如何寻找cost function J(w,b)=0的参数呢?
下面准备一组数量较多的训练数据:
x_train = np.array([1.0, 1.7, 2.0, 2.5, 3.0, 3.2])
y_train = np.array([250, 300, 480, 430, 630, 730,])plt.close('all')
fig, ax, dyn_items = plt_stationary(x_train, y_train)
updater = plt_update_onclick(fig, ax, x_train, y_train, dyn_items)结果为:


上面两张图中第一行右图是cost function 代价函数图,可以看出来多数据的情况下,很有可能是找不到代价函数为0的点的,这时只能寻找最小的点。当代价函数最小的时候,第一行左图中的线性模型与实际数据匹配度较高。
成本函数对损失进行平方的事实确保了“误差面”像汤碗一样凸起。它将始终具有一个最小值,可以通过遵循所有维度的梯度来达到该最小值。在前面的图中,由于w和b维度的比例不同,因此不容易识别。下面的图,其中w和b是对称的,可以发现,上图中的cost 图形,就是下图中这个碗被拍扁的状态。

梯度下降——自动寻找最小的cost function 代价函数
上一部分中代价函数是通过手动来调整的,在实际应用中手动调整是不现实的,因此需要一种方法来自动寻找最小的代价函数。
梯度的概念:
要引入梯度需要先知道方向导数这个东西。方向导数是函数定义域的内点对某一方向求导得到的导数。就是说函数上每一个点都有向各种方向变大变小的趋势,而方向导数就是函数上某一个点朝某一个方向上的导数。而同一个点上朝各个方向的导数大小是不一样的,梯度就是这些导数中变化量最大的那个方向。
具体分析可以参考知乎文章:通俗理解方向导数、梯度|学习笔记 - 知乎 (zhihu.com)
上一张AI大佬的图来直观感受一下梯度:
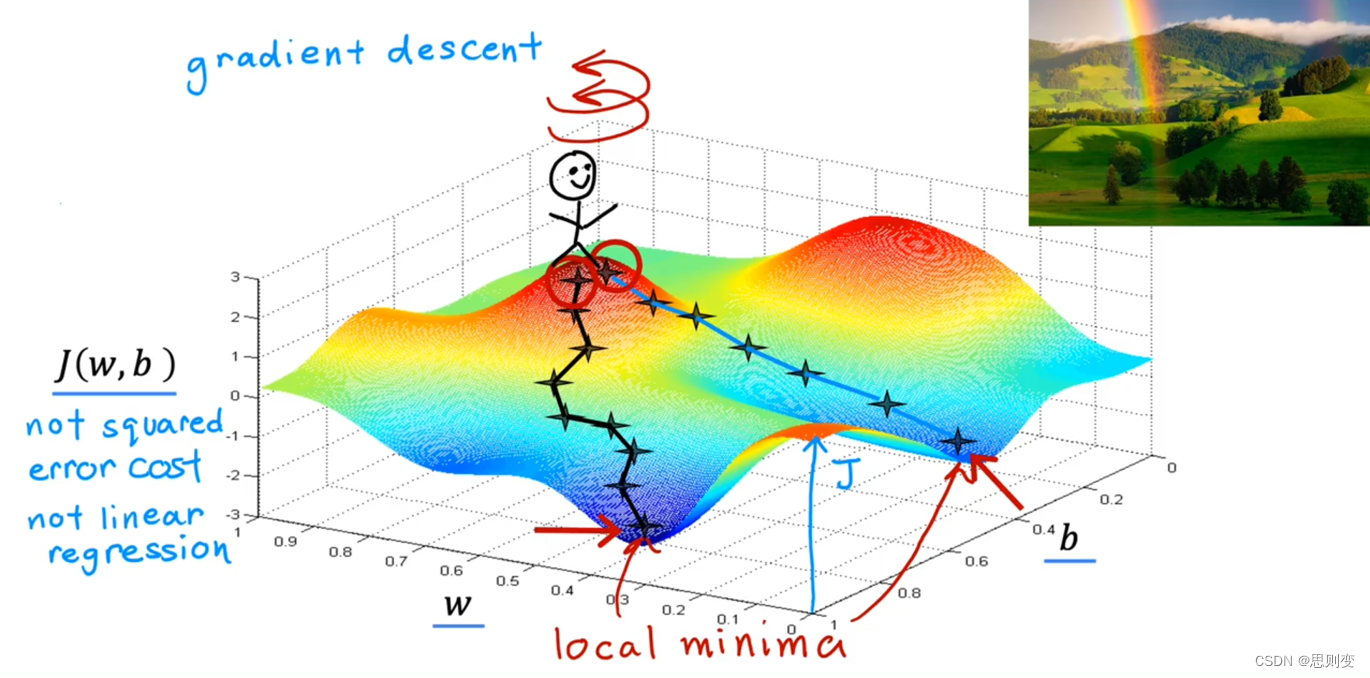
下山的路有很多条,只有沿梯度方向下山最快。因此我们要沿着梯度的方向来快速的寻找cost function的最小值。
梯度下降公式:

实现代码为:
代码实现了上面的公式4和公式5,也就是计算了w,b各自的偏导数。
def compute_gradient(x, y, w, b): """Computes the gradient for linear regression Args:x (ndarray (m,)): Data, m examples y (ndarray (m,)): target valuesw,b (scalar) : model parameters Returnsdj_dw (scalar): The gradient of the cost w.r.t. the parameters wdj_db (scalar): The gradient of the cost w.r.t. the parameter b """# Number of training examplesm = x.shape[0] dj_dw = 0dj_db = 0for i in range(m): f_wb = w * x[i] + b dj_dw_i = (f_wb - y[i]) * x[i] dj_db_i = f_wb - y[i] dj_db += dj_db_idj_dw += dj_dw_i dj_dw = dj_dw / m dj_db = dj_db / m return dj_dw, dj_db现在检验一下这个函数计算出来的是不是梯度:
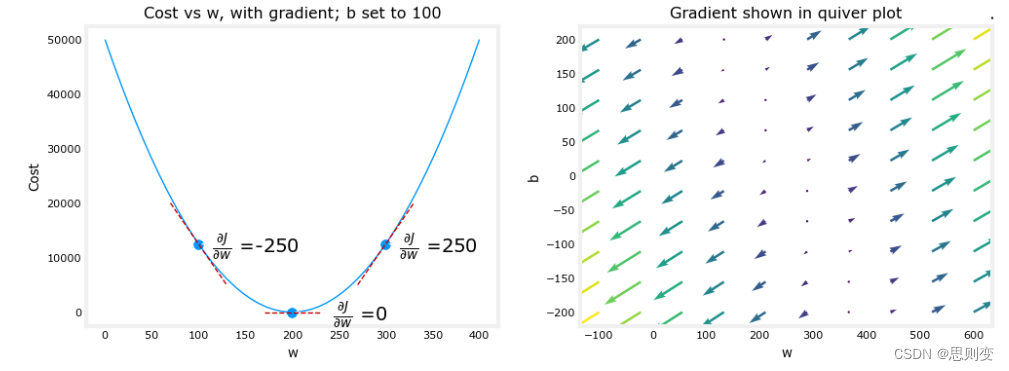
plt_gradients(x_train,y_train, compute_cost, compute_gradient)
plt.show()结果为:当w=200时,cost function 代价函数的值最小。下面右边的图中,在图的右侧,导数为正数,而在左侧为负数。由于“碗形”,导数将始终导致梯度下降到梯度为零的底部。
上面完成了梯度的计算,现在来进行梯度下降的代码实现:
def gradient_descent(x, y, w_in, b_in, alpha, num_iters, cost_function, gradient_function):"""Performs gradient descent to fit w,b. Updates w,b by takingnum_iters gradient steps with learning rate alphaArgs:x (ndarray (m,)) : Data, m examplesy (ndarray (m,)) : target valuesw_in,b_in (scalar): initial values of model parametersalpha (float): Learning ratenum_iters (int): number of iterations to run gradient descentcost_function: function to call to produce costgradient_function: function to call to produce gradientReturns:w (scalar): Updated value of parameter after running gradient descentb (scalar): Updated value of parameter after running gradient descentJ_history (List): History of cost valuesp_history (list): History of parameters [w,b]"""w = copy.deepcopy(w_in) # avoid modifying global w_in# An array to store cost J and w's at each iteration primarily for graphing laterJ_history = []p_history = []b = b_inw = w_infor i in range(num_iters):# Calculate the gradient and update the parameters using gradient_functiondj_dw, dj_db = gradient_function(x, y, w, b)# Update Parameters using equation (3) aboveb = b - alpha * dj_dbw = w - alpha * dj_dw# Save cost J at each iterationif i < 100000: # prevent resource exhaustionJ_history.append(cost_function(x, y, w, b))p_history.append([w, b])# Print cost every at intervals 10 times or as many iterations if < 10if i % math.ceil(num_iters / 10) == 0:print(f"Iteration {i:4}: Cost {J_history[-1]:0.2e} ",f"dj_dw: {dj_dw: 0.3e}, dj_db: {dj_db: 0.3e} ",f"w: {w: 0.3e}, b:{b: 0.5e}")return w, b, J_history, p_history # return w and J,w history for graphing梯度下降的代码已经完成,我们来通过下面的代码使用这个梯度下降算法寻找最优的模型:
假设初始的模型参数w_init和b_init 都是0,训练次数为10000次,学习率tmp_aplha为1.0e-2也就是0.01。然后打印出最终的参数w和b。
# 目前还是通过多次的迭代更新w,b,来确认最合适的w,b参数。有没可能不手动更新迭代次数,由模型自己寻找最佳参数
# initialize parameters
w_init = 0
b_init = 0
# some gradient descent settings
iteration = 10000
tmp_alpha = 1.0e-2# run gradient descent
w_final,b_final , J_hist, p_hist = gradient_descent(x_train,y_train,w_init,b_init,tmp_alpha,iteration,compute_cost,compute_gradient)print(f"(w,b) found by gradient descent: ({w_final:8.4f},{b_final:8.4f})")
最终输出为:w=200,b=100
Iteration 0: Cost 7.93e+04 dj_dw: -6.500e+02, dj_db: -4.000e+02 w: 6.500e+00, b: 4.00000e+00
Iteration 1000: Cost 3.41e+00 dj_dw: -3.712e-01, dj_db: 6.007e-01 w: 1.949e+02, b: 1.08228e+02
Iteration 2000: Cost 7.93e-01 dj_dw: -1.789e-01, dj_db: 2.895e-01 w: 1.975e+02, b: 1.03966e+02
Iteration 3000: Cost 1.84e-01 dj_dw: -8.625e-02, dj_db: 1.396e-01 w: 1.988e+02, b: 1.01912e+02
Iteration 4000: Cost 4.28e-02 dj_dw: -4.158e-02, dj_db: 6.727e-02 w: 1.994e+02, b: 1.00922e+02
Iteration 5000: Cost 9.95e-03 dj_dw: -2.004e-02, dj_db: 3.243e-02 w: 1.997e+02, b: 1.00444e+02
Iteration 6000: Cost 2.31e-03 dj_dw: -9.660e-03, dj_db: 1.563e-02 w: 1.999e+02, b: 1.00214e+02
Iteration 7000: Cost 5.37e-04 dj_dw: -4.657e-03, dj_db: 7.535e-03 w: 1.999e+02, b: 1.00103e+02
Iteration 8000: Cost 1.25e-04 dj_dw: -2.245e-03, dj_db: 3.632e-03 w: 2.000e+02, b: 1.00050e+02
Iteration 9000: Cost 2.90e-05 dj_dw: -1.082e-03, dj_db: 1.751e-03 w: 2.000e+02, b: 1.00024e+02
(w,b) found by gradient descent: (199.9929,100.0116)上面可以尝试迭代次数不同的情况下,得出的w和b是不一样的。目前还是通过手更新迭代次数来寻找w,b,有没有可能不需要人的干预就能实现模型自己学习,自己寻找最佳的w,b组合,后面的CNN应该能做到这一点。
至此,线性模型的实现,模型性能的衡量参数,模型最佳参数的训练方法基本就整理清楚了。
相关文章:

[Machine Learning][Part 2]监督学习的实现
目录 线性模型实现: cost function :代价函数或者损失函数——衡量模型优劣的一个指标 理论: 代码实现: 梯度下降——自动寻找最小的cost function 代价函数 梯度的概念: 梯度下降公式: 实现一个简单的监督学习…...
【计算机毕业设计】基于SpringBoot+Vue大学生心理健康管理系统的开发与实现
博主主页:一季春秋博主简介:专注Java技术领域和毕业设计项目实战、Java、微信小程序、安卓等技术开发,远程调试部署、代码讲解、文档指导、ppt制作等技术指导。主要内容:毕业设计(Java项目、小程序等)、简历模板、学习资料、面试题…...
下载水果FLStudio21.2软件安装更新教程
编曲是一种对音乐创作过程中涉及的元素和步骤进行组织和安排的艺术形式。对于想要学习编曲的人来说,以下是一些有用的建议: 1. 学习基础知识 在开始学习编曲之前,你需要掌握一些基础知识,例如音乐理论、乐器演奏和数字音乐制作技…...
人工智能机器学习-飞桨神经网络与深度学习
飞桨神经网络与深度学习-机器学习 目录 飞桨神经网络与深度学习-机器学习 1.机器学习概述 2.机器学习实践五要素 2.1.数据 2.2.模型 2.3.学习准则 2.4.优化算法 2.5.评估标准 3.实现简单的线性回归模型 3.1.数据集构建 3.2.模型构建 3.3.损失函数 3.4.模型优化 3…...

linux部署页面内容
/bin:该目录包含了常用的二进制可执行文件,如ls、cp、mv、rm等等。 /boot:该目录包含了启动Linux系统所需的文件,如内核文件和引导加载程序。 /dev:该目录包含了所有设备文件,如硬盘、光驱、鼠标、键盘等等…...
若依框架集成WebSocket带用户信息认证
一、WebSocket 基础知识 我们平时前后台请求用的最多的就是 HTTP/1.1协议,它有一个缺陷, 通信只能由客户端发起,如果想要不断获取服务器信息就要不断轮询发出请求,那么如果我们需要服务器状态变化的时候能够主动通知客户端就需要用…...
0基础学习VR全景平台篇 第101篇:企业版功能-子账号分配管理
大家好,欢迎观看蛙色VR官方系列——后台使用课程! 本期为大家带来蛙色VR平台,企业版教程-子账号分配管理功能! 功能位置示意 一、本功能将用在哪里? 子账号分配管理功能,主要用于企业版用户为自己服务的终…...

adb 命令集
adb 查看app启动时间 1.清除时间 adb shell am start -S com.android.systemui/.SystemUIService2.启动应用并记录 adb shell am start -W <PACKAGE_NAME>/.<ACTIVITY_NAME>TotalTime: 491 adb 查看分辨率、dpi 分辨率 adb shell wm sizePhysical size: 1080…...

分享78个Python源代码总有一个是你想要的
分享78个Python源代码总有一个是你想要的 源码下载链接:https://pan.baidu.com/s/1ZhXDsVuYsZpOUQIUjHU2ww?pwd8888 提取码:8888 下面是文件的名字。 12个python项目源码 Apache Superset数据探查与可视化平台v2.0.1 API Star工具箱v0.7.2 Archery…...
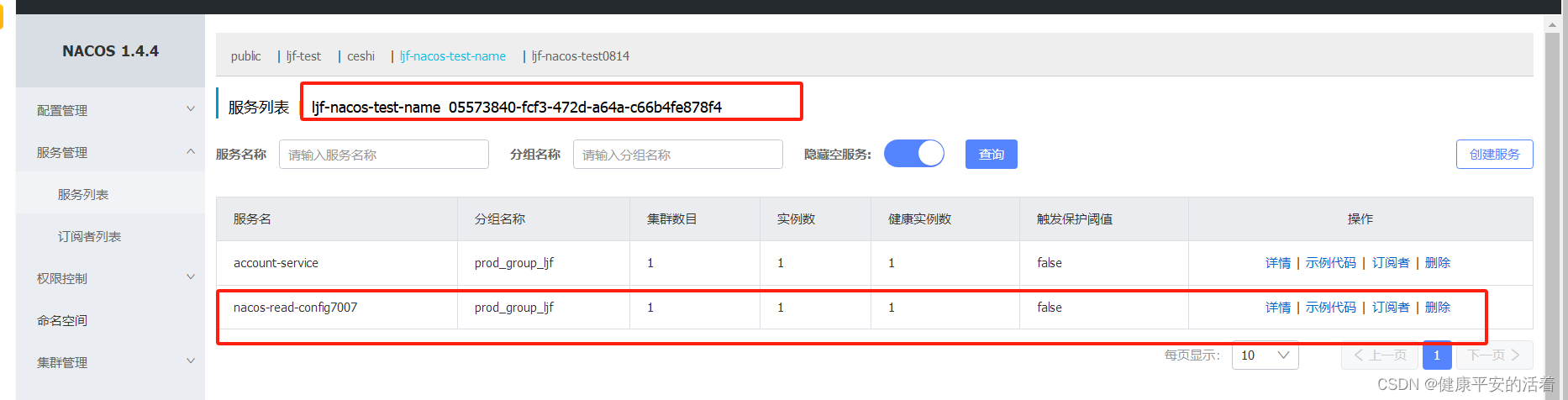
springcloud3 指定nacos的服务名称和配置文件的group,名称空间
一 指定读取微服务的配置文件 1.1 工程结构 1.2 nacos的配置 1.配置文件 2.内容 1.3 微服务的配置文件 1.bootstrap.yml内容 2.application.yml文件内容 1.4 验证访问 控制台: 1.5 nacos服务空间名称和groupid配置 1.配置文件配置 2.nacos的查看...

go-redis简单使用
目录 一:官方文档和安装方式二:简单案例使用 一:官方文档和安装方式 官方中文文档:https://redis.uptrace.dev/zh/guide/go-redis.html安装:go get github.com/redis/go-redis/v9 二:简单案例使用 简单的…...

33. 搜索旋转排序数组-二重二分查找
33. 搜索旋转排序数组-二分查找 整数数组 nums 按升序排列,数组中的值 互不相同 。 在传递给函数之前,nums 在预先未知的某个下标 k(0 < k < nums.length)上进行了 旋转,使数组变为 [nums[k], nums[k1], …, n…...
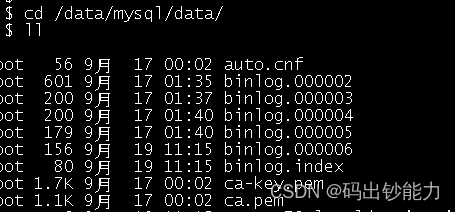
mysql自动删除过期的binlog
一、binlog_expire_logs_seconds 配置项 mysql 8.0使用配置项 binlog_expire_logs_seconds 设置binlog过期时间,单位为秒。 mysql旧版本使用配置项 expire_logs_days 设置binlog过期时间,单位为天,不方便测试。 在 8.0 使用 expire_logs_d…...

Java面向对象(1)
static静态变量 public class Student {static String name;private double score;public Student(){};public Student(double score) {this.score score;}public double getScore() {return score;}public void setScore(double score) {this.score score;} }public class t…...
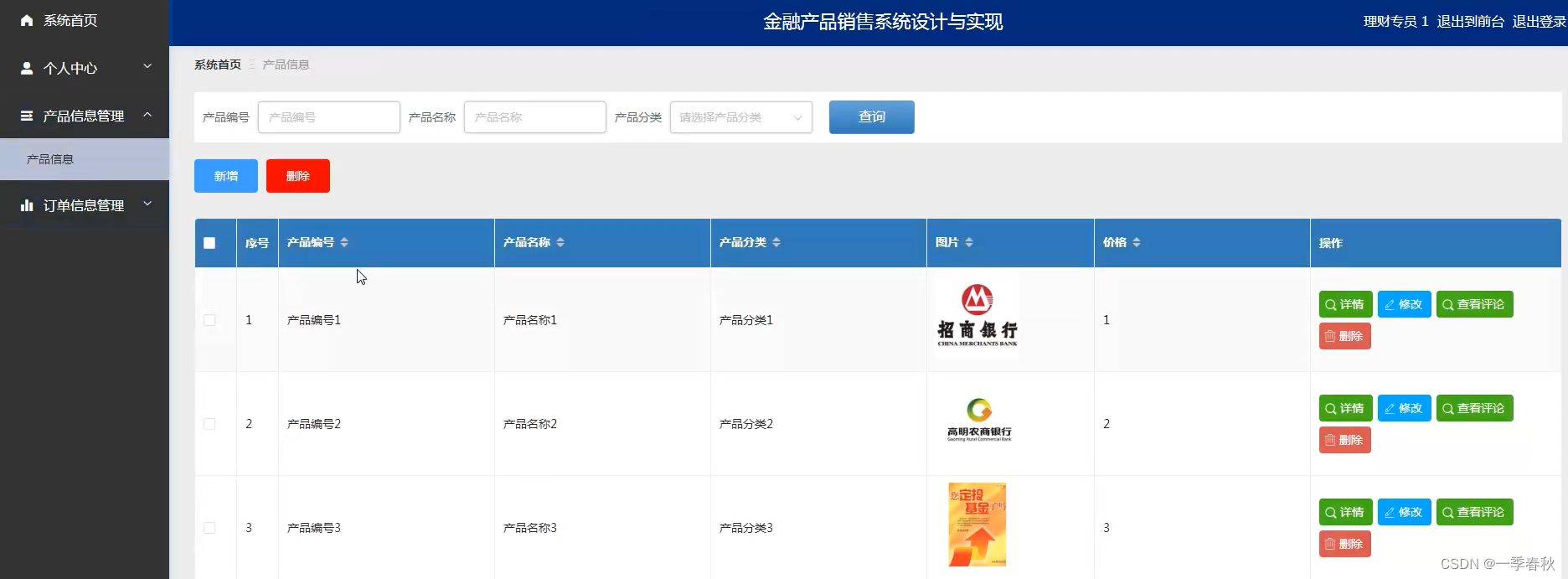
【计算机毕业设计】基于SpringBoot+Vue金融产品销售系统的设计与实现
博主主页:一季春秋博主简介:专注Java技术领域和毕业设计项目实战、Java、微信小程序、安卓等技术开发,远程调试部署、代码讲解、文档指导、ppt制作等技术指导。主要内容:毕业设计(Java项目、小程序、安卓等)、简历模板、学习资料、…...

【面试题精讲】Mysql如何实现乐观锁
❝ 有的时候博客内容会有变动,首发博客是最新的,其他博客地址可能会未同步,认准https://blog.zysicyj.top ❞ 首发博客地址 文章更新计划 系列文章地址 在 MySQL 中,可以通过使用乐观锁来实现并发控制,以避免数据冲突和并发更新问…...
从零开始搭建java web springboot Eclipse MyBatis jsp mysql开发环境
文章目录 1 第一步软件安装1.1 下载并安装Eclipse1.2 下载并安装Java1.3 下载并安装Apache Maven1.4 下载并安装MySQL 2 创建所需要的表和数据3 创建Maven 工程、修改jdk4 通过pom.xml获取所需要的jar包5 安装Eclipse的MyBatis插件6 创建文件夹以及jsp文件7 创建下面各种java类…...

【VsCode】整理代码
在VsCode中,你可以使用插件"Beautify"来格式化你的HTML代码,使其更加整齐清晰。而对于JSON代码,你可以使用"vscode-json"插件来格式化为易读的树状结构,方便查看和编辑。这些插件可以帮助你更加高效地整理HTM…...

盘点总结汇总植物病虫害、人体疾病识别相关的项目实践
在前面的很多项目中做了许多有关于植物病虫害比如:苹果病虫害、番茄病虫害、小麦病虫害、辣椒病虫害、白菜病虫害、木薯病虫害、葡萄病虫害、柑橘病虫害等等,还有一些是有关于人体疾病识别相关的,比如:病理细胞识别、癌症识别、皮…...
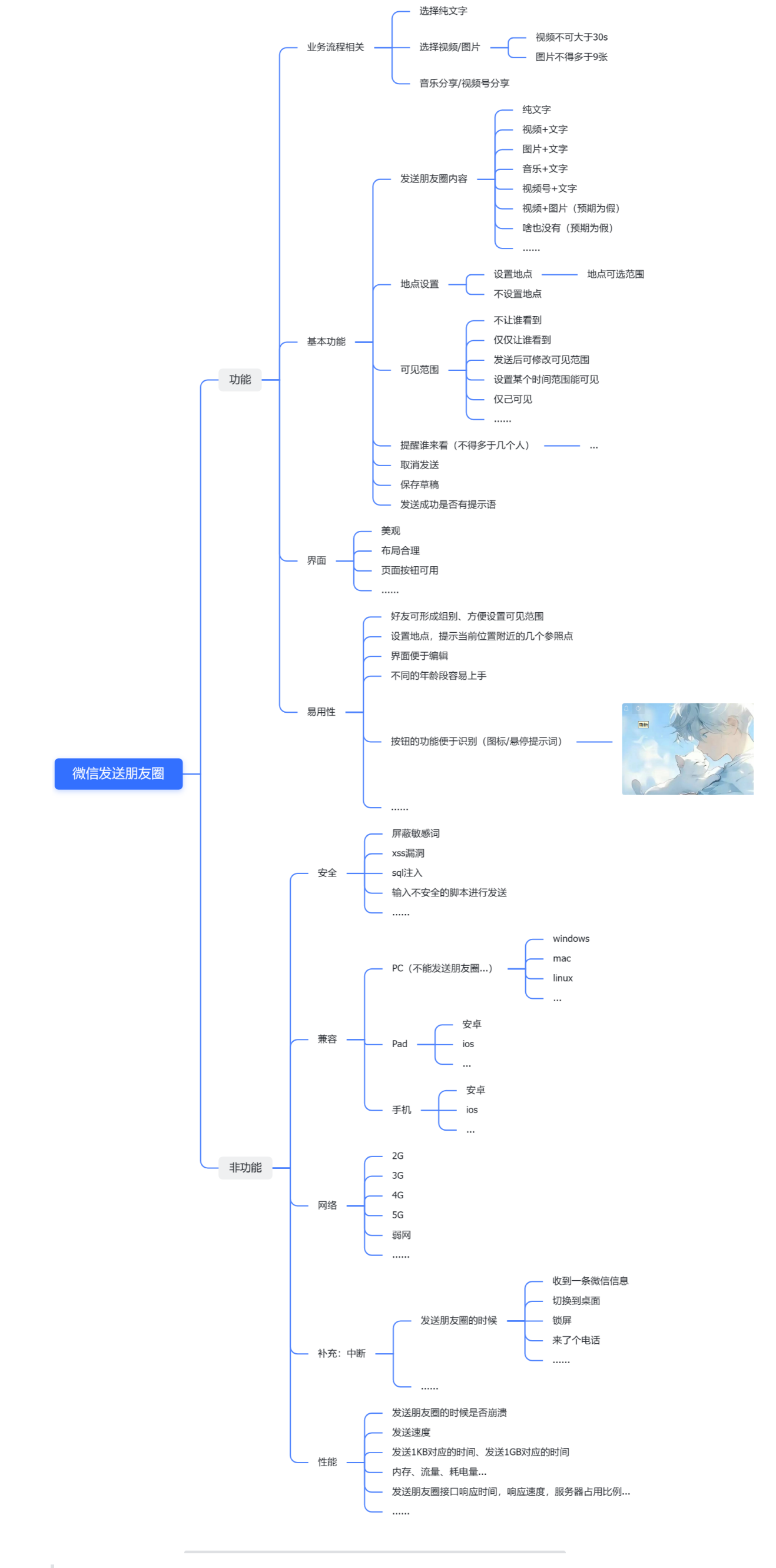
【测试开发】用例篇 · 熟悉黑盒测试用例设计方法(2)· 正交表 · 场景设计 · 常见案例练习
【测试开发】用例篇(2) 文章目录 【测试开发】用例篇(2)1. 正交表法1.1 什么是正交表1.2 两个重要概念1.3 如何通过正交表设计测试用例1.3.1 充分理解需求1.3.2 确定因素、确定水平1.3.3 allpairs画正交表1.3.4 补充正交表1.3.5 将…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

MySQL 部分重点知识篇
一、数据库对象 1. 主键 定义 :主键是用于唯一标识表中每一行记录的字段或字段组合。它具有唯一性和非空性特点。 作用 :确保数据的完整性,便于数据的查询和管理。 示例 :在学生信息表中,学号可以作为主键ÿ…...

深入理解Optional:处理空指针异常
1. 使用Optional处理可能为空的集合 在Java开发中,集合判空是一个常见但容易出错的场景。传统方式虽然可行,但存在一些潜在问题: // 传统判空方式 if (!CollectionUtils.isEmpty(userInfoList)) {for (UserInfo userInfo : userInfoList) {…...

「全栈技术解析」推客小程序系统开发:从架构设计到裂变增长的完整解决方案
在移动互联网营销竞争白热化的当下,推客小程序系统凭借其裂变传播、精准营销等特性,成为企业抢占市场的利器。本文将深度解析推客小程序系统开发的核心技术与实现路径,助力开发者打造具有市场竞争力的营销工具。 一、系统核心功能架构&…...

第八部分:阶段项目 6:构建 React 前端应用
现在,是时候将你学到的 React 基础知识付诸实践,构建一个简单的前端应用来模拟与后端 API 的交互了。在这个阶段,你可以先使用模拟数据,或者如果你的后端 API(阶段项目 5)已经搭建好,可以直接连…...

前端开发者常用网站
Can I use网站:一个查询网页技术兼容性的网站 一个查询网页技术兼容性的网站Can I use:Can I use... Support tables for HTML5, CSS3, etc (查询浏览器对HTML5的支持情况) 权威网站:MDN JavaScript权威网站:JavaScript | MDN...

基于开源AI智能名片链动2 + 1模式S2B2C商城小程序的沉浸式体验营销研究
摘要:在消费市场竞争日益激烈的当下,传统体验营销方式存在诸多局限。本文聚焦开源AI智能名片链动2 1模式S2B2C商城小程序,探讨其在沉浸式体验营销中的应用。通过对比传统品鉴、工厂参观等初级体验方式,分析沉浸式体验的优势与价值…...
