2024年考研教育专业的教育综合考试大纲、样题和往年真题
根据教育部通知,2024年全国硕士研究生招生考试初试定于2023年12月23日至24日,即我们说的2024年考研时间为12月23-24日。距离现在只剩下3个月不到的时间,那么如何让我们在最后三个月内的复习和备考有效且高效呢?

结合很多清北复交研究生的备考经验,建议大家这么做:对照着考试大纲查漏补缺。
很多考研的小伙伴都是从大三就开始准备了,所以课本和教材相信大家都已经很熟悉了,那么在最后三个月冲刺的时间就对照着大纲,一条一条的过,看看是不是理解了,并且结合往年的真题想一想,这一条会怎么考。如果每一条都想明白了、都理解了,那么考试自然就不成问题了。
所以,了解考试大纲是很重要的,这是我们考研冲刺阶段的指南针和方向。
目前,教育部门也在陆续发布2024年考研的大纲,目前已经发布了教育综合和法硕的考试大纲,本文将给大家介绍教育综合的考试大纲、样题和过去四年的真题,供大家备考了解,提高您的备考效率。

一、2024年教育综合科目试卷满分及考试时间
满分为 150 分,考试时间为 180 分钟。
二、2024年教育综合科目试卷内容结构
- 教育学原理 约 60 分
- 中外教育史 约 50 分
- 教育心理学 约 40 分
(注:中外教育史包含中国教育史、外国教育史)
三、2024年教育综合科目试卷题型结构
- 单项选择题:30 小题,每小题 2 分,共 60 分
- 论述题:2 小题,每小题 15 分,共 30 分
- 材料分析题:4 小题,每小题 15 分,共 60 分
四、2024年教育综合科目的考查目标
1、教育学原理的考查目标
- 准确识记教育学的基础知识。
- 正确理解教育学的基本概念和基本理论。
- 能够运用教育学的基本理论分析教育理论与实践问题
2、中外教育史的考查目标
- 系统掌握中外教育史的基本知识,把握教育思想演变、教育制度发展、教育实施进
- 程的基本线索与阶段,特别是代表性教育家的教育思想、重要的教育制度、重大的教育事件。
- 准确理解有关中外教育史的基本文献,特别是其中的代表性材料,培养严谨的学风。
- 正确运用辩证唯物主义和历史唯物主义的观点分析、评价中外教育历史事实,总结
- 经验与教训,为现实的教育改革与发展提供理论启示。
3、教育心理学的考查目标
- 识记与了解教育心理学的发展历程、代表人物及其主要实验。
- 理解和掌握教育心理学的基本概念、基本原理及其对教育工作的启示。
- 运用教育心理学的基本规律和主要理论,解释有关教育现象,解决有关实际问题。
五、2024年教育综合科目的样卷和历年真题
在教育部教育考试院发布的考试大纲中,附了一份样卷,我也把近四年的教育综合科目的考研真题和答案进行了整理,如果有需要可以找我要。

其他考试科目的大纲和真题、答案我也在陆续整理中,有需要的小伙伴欢迎沟通。
祝所有的小伙伴考研顺利,都能实现自己的理想和追求!
相关文章:

2024年考研教育专业的教育综合考试大纲、样题和往年真题
根据教育部通知,2024年全国硕士研究生招生考试初试定于2023年12月23日至24日,即我们说的2024年考研时间为12月23-24日。距离现在只剩下3个月不到的时间,那么如何让我们在最后三个月内的复习和备考有效且高效呢? 结合很多清北复交研…...
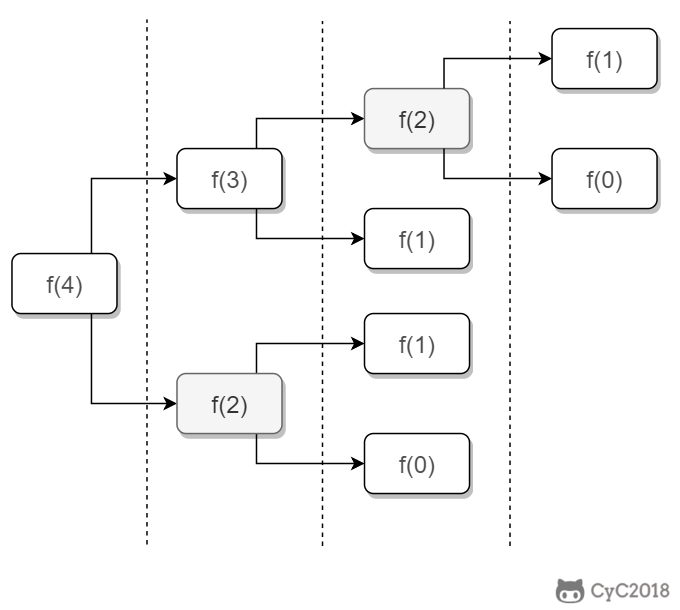
算法之斐波那契数列
10.1 斐波那契数列 题目链接 牛客网 题目描述 求斐波那契数列的第 n 项,n < 39。 解题思路 如果使用递归求解,会重复计算一些子问题。例如,计算 f(4) 需要计算 f(3) 和 f(2),计算 f(3) 需要计算 f(2) 和 f(1),…...
关于Pandas数据分析
pandas的数据加载与预处理 数据清洗:洗掉脏数据 整理分析:字不如表 数据展现:表不如图 环境搭建 pythonjupyter anaconda Jupyter Notebook Jupyter Notebook可以在网页页面中直接编写代码和运行代码, 代码的运行结果也会直接在代码块下显示…...
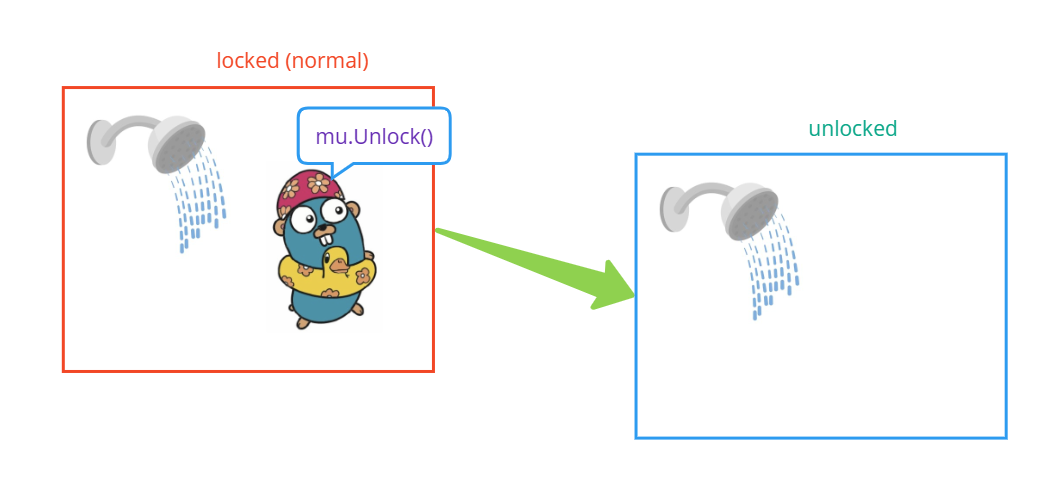
Go 并发可视化解释 - sync.Mute
在学习 Go 编程语言时,您可能会遇到这句著名的格言:“不要通过共享内存来进行通信;相反,通过通信来共享内存。” 这句话构成了 Go 强大并发模型的基础,其中通道(channels)作为协程之间的主要通信…...
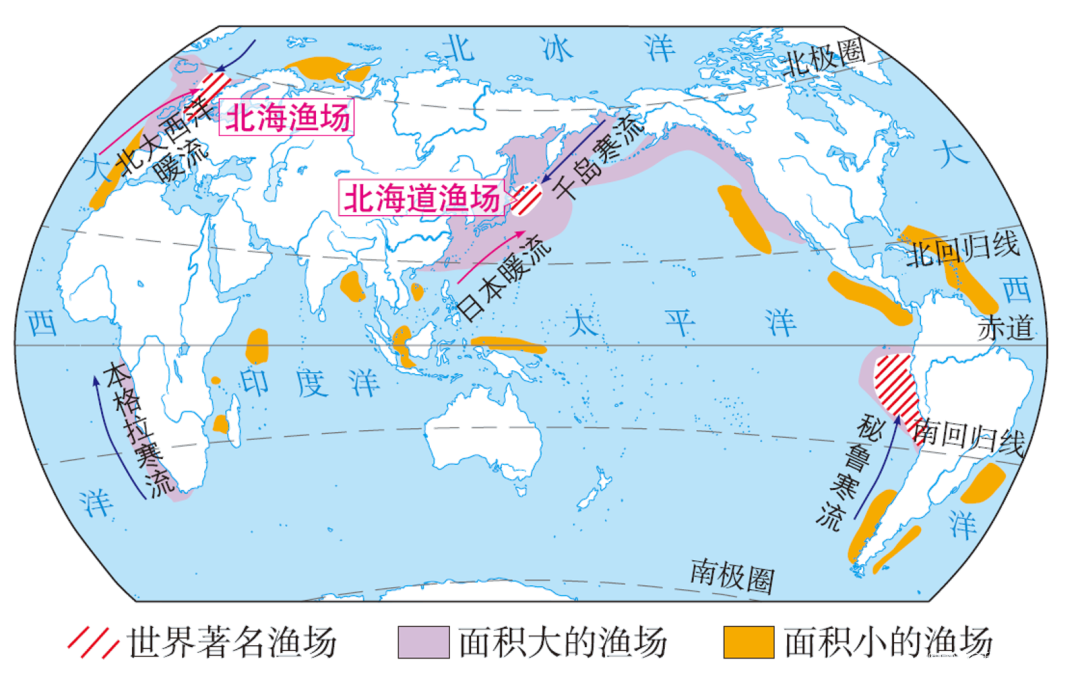
十几张高清世界地图
十几张高清世界地图 仅供学习!...
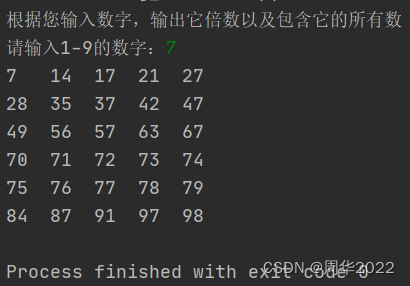
Python 逢七拍手游戏
"""逢七拍手游戏介绍:逢七拍手游戏的规则是:从1开始顺序数数,数到有7,或者是7的倍数时,就拍一手。例如:7、14、17......70......知识点:1、循环语句for2、嵌套条件语句if/elif/e…...
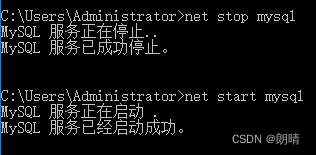
Windows安装Mysql--免安装版
在Windows系统上安装免安装版MySql的步骤 官方下载地址:https://dev.mysql.com/downloads/mysql/ 将下载好的文件“mysql-5.7.18-winx64”解压缩到C盘的 目录下: 配置环境变量: (略) 正式安装,添加my.i…...

TypeScript中常见的操作符运算符总结
一、非空断言操作符(!) 当我们⽆法断定类型时,可以使用后缀表达式操作符 ! 来断⾔操作对象是⾮ null 或⾮ undefined 类型。 具体来说,比如表达式: x ! , 结果将从 x 值域中排除 null 和 unde…...

什么是泛型约束?
泛型约束(Generic Constraints)是一种在使用泛型时限制可接受类型的方式。它允许我们对泛型类型参数进行限定,以确保只有符合特定条件的类型才能被使用。 泛型约束的作用是提供更精确的类型控制和更强的类型安全性。通过约束泛型类型参数&am…...

代码随想录算法训练营 动态规划part11
一、买卖股票的最佳时机III 123. 买卖股票的最佳时机 III - 力扣(LeetCode) 请选一个喜欢的吧/(ㄒoㄒ)/~~123. 买卖股票的最佳时机 III - 力扣(LeetCode) class Solution {public int maxProfit(int[] prices) {if(pricesnul…...
复习——Lesson 16 - Lesson20)
新概念英语(第二册)复习——Lesson 16 - Lesson20
前言 新概念英语的16-20课,从21课开始,每天一课的速度更新,方便你能快速跟上。 文章目录 前言Lesson 16 - A polite request原文译文单词 Lesson 17 - Always Young原文译文单词 Lesson 18 - He often does this!原文译文单词Lesson 19 - So…...

[题] n-皇后问题 #深搜 #DFS
题目 AcWing 843. n-皇后问题 代码 #include<bits/stdc.h> using namespace std; const int N 20; int n, p[N]; char g[N][N]; bool col[N], dg[N], udg[N]; void D (int u){if(u n){for(int j 0; j < n; j )puts(g[j]);cout << endl;return ;}for(int i…...

十小时开源了一个加密算法仓库,功能强大,后端开发人员狂喜!
写在前面 昨晚上睡觉前我就在想能不能把多个加密算法集成到一个库中,方便开发者调用,说干就干,今天肝了一天,中午直接吃的外卖哈哈哈哈,终于把仓库开源了,欢迎各位Go开发者Star和Fork! 仓库地址 go-cryp…...

标准化套利的使用
交易对象:目前使用郑商所,大商所的spd标准化套利组合进行交易。 交易平台:易盛极星极星产品网 手续费研究:白糖期货手续费和保证金2023年09月更新 - 九期网 本人使用的期货交易公司:中信期货(幸亏资金量大ÿ…...
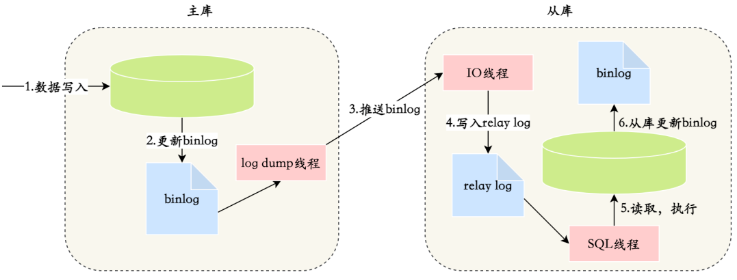
【MySQL数据库事务操作、主从复制及Redis数据库读写分离、主从同步的实现机制】
文章目录 MySQL数据库事务操作、主从复制及Redis数据库读写分离、主从同步的实现机制ACID及如何实现事务隔离级别:MVCC 多版本并发控制MySQL数据库主从复制主从同步延迟怎么处理Redis 读写分离1.什么是主从复制2.读写分离的优点 Redis为什么快呢? MySQL数…...
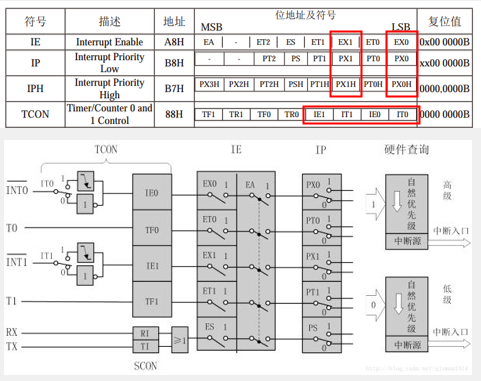
十五、红外遥控器
十五、红外遥控器 介绍基本接收和发送遥控器键码外部中断和外部中断寄存器 红外解码中断函数红外遥控电机模块电机调速 介绍 基本接收和发送 空闲状态:红外LED不亮,接收头输出高电平发送低电平:红外LED以38KHz闪烁,接收头输出低…...

diot函数解析
文章目录 前言一、Rio_readinitb二、Rio_readlineb三、strstr四、strcat五、Open_clientfd六、Rio_writen总结 前言 备战CSAPP中的ProxyLab时解析书上的diot函数中遇到了一些不会的函数,遂解析记录。 一、Rio_readinitb 读和解析请求行 Rio_readinitb(&rio,…...

Python函数绘图与高等代数互融实例(一):正弦函数与余弦函数
Python函数绘图与高等代数互融实例(一):正弦函数与余弦函数 Python函数绘图与高等代数互融实例(二):闪点函数 Python函数绘图与高等代数互融实例(三):设置X|Y轴|网格线 Python函数绘图与高等代数互融实例(四):设置X|Y轴参考线|参考区域 Python函数绘图与高等代数互融实例(五…...
Python 判断回文数
"""判断输入的数是否为回文数介绍:回文数:数字从高位到低位正序排列和低位到高位逆序排列都是同一数值例如:数字 1221 无论正序还是逆序都是 1221知识点:1、获取字符串长度函数len()2、条件语句if/elif/else3、循环…...

人工智能在金融领域的五个应用案例
随着科技的进步,人工智能(Artificial Intelligence,AI)正逐渐渗透到各个行业中,其中包括金融领域。本文介绍人工智能在金融领域的五个应用案例,以期帮助大家更好地了解这个新兴技术在金融中的价值和作用。 文章目录 Part1 风险管理…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...

R 语言科研绘图第 55 期 --- 网络图-聚类
在发表科研论文的过程中,科研绘图是必不可少的,一张好看的图形会是文章很大的加分项。 为了便于使用,本系列文章介绍的所有绘图都已收录到了 sciRplot 项目中,获取方式: R 语言科研绘图模板 --- sciRplothttps://mp.…...

第7篇:中间件全链路监控与 SQL 性能分析实践
7.1 章节导读 在构建数据库中间件的过程中,可观测性 和 性能分析 是保障系统稳定性与可维护性的核心能力。 特别是在复杂分布式场景中,必须做到: 🔍 追踪每一条 SQL 的生命周期(从入口到数据库执行)&#…...

日常一水C
多态 言简意赅:就是一个对象面对同一事件时做出的不同反应 而之前的继承中说过,当子类和父类的函数名相同时,会隐藏父类的同名函数转而调用子类的同名函数,如果要调用父类的同名函数,那么就需要对父类进行引用&#…...

数据结构:泰勒展开式:霍纳法则(Horner‘s Rule)
目录 🔍 若用递归计算每一项,会发生什么? Horners Rule(霍纳法则) 第一步:我们从最原始的泰勒公式出发 第二步:从形式上重新观察展开式 🌟 第三步:引出霍纳法则&…...
