Python|每日一练|栈|数组|字典树|数组|树|广度优先搜索|单选记录:逆波兰表达式求值|回文对|二叉树的层序遍历
1、逆波兰表达式求值(栈,数组)
根据 逆波兰表示法(https://baike.baidu.com/item/%E9%80%86%E6%B3%A2%E5%85%B0%E5%BC%8F/128437),求表达式的值。
有效的算符包括 +、-、*、/ 。每个运算对象可以是整数,也可以是另一个逆波兰表达式。
说明:
- 整数除法只保留整数部分。
- 给定逆波兰表达式总是有效的。换句话说,表达式总会得出有效数值且不存在除数为 0 的情况。
示例 1:
输入:tokens = ["2","1","+","3","*"]
输出:9
解释:该算式转化为常见的中缀算术表达式为:((2 + 1) * 3) = 9
示例 2:
输入:tokens = ["4","13","5","/","+"]
输出:6
解释:该算式转化为常见的中缀算术表达式为:(4 + (13 / 5)) = 6
示例 3:
输入:tokens = ["10","6","9","3","+","-11","*","/","*","17","+","5","+"]
输出:22
解释:
该算式转化为常见的中缀算术表达式为:
((10 * (6 / ((9 + 3) * -11))) + 17) + 5
= ((10 * (6 / (12 * -11))) + 17) + 5
= ((10 * (6 / -132)) + 17) + 5
= ((10 * 0) + 17) + 5
= (0 + 17) + 5
= 17 + 5
= 22
提示:
- 1 <= tokens.length <= 104
- tokens[i] 要么是一个算符("+"、"-"、"*" 或 "/"),要么是一个在范围 [-200, 200] 内的整数
逆波兰表达式:
逆波兰表达式是一种后缀表达式,所谓后缀就是指算符写在后面。
- 平常使用的算式则是一种中缀表达式,如 ( 1 + 2 ) * ( 3 + 4 ) 。
- 该算式的逆波兰表达式写法为 ( ( 1 2 + ) ( 3 4 + ) * ) 。
逆波兰表达式主要有以下两个优点:
- 去掉括号后表达式无歧义,上式即便写成 1 2 + 3 4 + * 也可以依据次序计算出正确结果。
- 适合用栈操作运算:遇到数字则入栈;遇到算符则取出栈顶两个数字进行计算,并将结果压入栈中。
选项代码:
class Solution(object):def evalRPN(self, tokens):""":type tokens: List[str]:rtype: int"""stack = []for token in tokens:if token not in ["+", "%", "*", "/"]:stack.append(int(token))else:num1 = stack.pop()num2 = stack.pop()if token == "+":stack.append(num1 + num2)elif token == "-":stack.append(num2 - num1)elif token == "*":stack.append(num1 * num2)elif token == "/":if num1 * num2 < 0:result = -((-num2) // num1)stack.append(result)else:stack.append(num2 // num1)print(stack)return stack.pop()
# %%
if __name__ == "__main__":tokens = ["10","6","9","3","+","-11","*","/","*","17","+","5","+"]sol = Solution()result = sol.evalRPN(tokens)print(result)PS:逆波兰式
(Reverse Polish Notation,RPN,或逆波兰记法),也叫后缀表达式(将运算符写在操作数之后)。
算法定义
一个表达式E的后缀形式可以如下定义:
(1)如果E是一个变量或常量,则E的后缀式是E本身。
(2)如果E是E1 op E2形式的表达式,这里op是任何二元操作符,则E的后缀式为E1'E2' op,这里E1'和E2'分别为E1和E2的后缀式。
(3)如果E是(E1)形式的表达式,则E1的后缀式就是E的后缀式。
如:我们平时写a+b,这是中缀表达式,写成后缀表达式就是:ab+
(a+b)*c-(a+b)/e的后缀表达式为:
(a+b)*c-(a+b)/e
→((a+b)*c)((a+b)/e)-
→((a+b)c*)((a+b)e/)-
→(ab+c*)(ab+e/)-
→ab+c*ab+e/-
算法作用
实现逆波兰式的算法,难度并不大,但为什么要将看似简单的中缀表达式转换为复杂的逆波兰式?原因就在于这个简单是相对人类的思维结构来说的,对计算机而言中序表达式是非常复杂的结构。相对的,逆波兰式在计算机看来却是比较简单易懂的结构。因为计算机普遍采用的内存结构是栈式结构,它执行先进后出的顺序。
2、回文对(字典树,数组)
给定一组 互不相同 的单词, 找出所有 不同 的索引对 (i, j),使得列表中的两个单词, words[i] + words[j] ,可拼接成回文串。
示例 1:
输入:words = ["abcd","dcba","lls","s","sssll"]
输出:[[0,1],[1,0],[3,2],[2,4]]
解释:可拼接成的回文串为 ["dcbaabcd","abcddcba","slls","llssssll"]
示例 2:
输入:words = ["bat","tab","cat"]
输出:[[0,1],[1,0]]
解释:可拼接成的回文串为 ["battab","tabbat"]
示例 3:
输入:words = ["a",""]
输出:[[0,1],[1,0]]
提示:
- 1 <= words.length <= 5000
- 0 <= words[i].length <= 300
- words[i] 由小写英文字母组成
选项代码:
from typing import List
class Solution:def palindromePairs(self, words: List[str]) -> List[List[int]]:def is_palindrome(str, start, end):"""检查子串是否是回文串"""part_word = str[start : end + 1]return part_word == part_word[::-1]def find_reversed_word(str, start, end):"""查找子串是否在哈希表中Return:不在哈希表中,返回 -1否则返回对应的索引"""part_word = str[start : end + 1]ret = hash_map.get(part_word, -1)return rethash_map = {}for i in range(len(words)):word = words[i][::-1]hash_map[word] = ires = []for i in range(len(words)):word = words[i]word_len = len(word)if is_palindrome(word, 0, word_len - 1) and "" in hash_map and word != "":res.append([hash_map.get(""), i])for j in range(word_len):if is_palindrome(word, j, word_len - 1):left_part_index = find_reversed_word(word, 0, j - 1)if left_part_index != -1 and left_part_index != i:res.append([i, left_part_index])if is_palindrome(word, 0, j - 1):right_part_index = find_reversed_word(word, j, word_len - 1)if right_part_index != -1 and right_part_index != i:res.append([right_part_index, i])return res
# %%
if __name__ == "__main__":words = ["a",""]sol = Solution()result = sol.palindromePairs(words)print(result)3、二叉树的层序遍历(树,广度优先搜索)
给你一个二叉树,请你返回其按 层序遍历 得到的节点值。 (即逐层地,从左到右访问所有节点)。
示例:
二叉树:[3,9,20,null,null,15,7], #!python中用None
3
/ \
9 20
/ \
15 7
返回其层序遍历结果:
[
[3],
[9,20],
[15,7]
]
选项代码:
class TreeNode:def __init__(self, x):self.val = xself.left = Noneself.right = Noneclass Solution(object):def levelOrder(self, root):""":type root: TreeNode:rtype: List[List[int]]"""if not root:return []queue, res = [root], []while queue:size = len(queue)temp = []for i in range(size):data = queue.pop(0)temp.append(data.val)if data.left:queue.append(data.left)if data.right:queue.append(data.right)res.append(temp)return res相关文章:

Python|每日一练|栈|数组|字典树|数组|树|广度优先搜索|单选记录:逆波兰表达式求值|回文对|二叉树的层序遍历
1、逆波兰表达式求值(栈,数组) 根据 逆波兰表示法(https://baike.baidu.com/item/%E9%80%86%E6%B3%A2%E5%85%B0%E5%BC%8F/128437),求表达式的值。 有效的算符包括 、-、*、/ 。每个运算对象可以是整数,也可以是另一个…...

慧教室系统--远程控制系统
随着科技的不断进步,越来越多的教育机构开始使用智慧教室系统来提升教学效果和学生体验。智慧教室系统不仅可以自动化管理设备,还可以实现远程控制,帮助教师和学生更加便捷地使用教室设备。智慧教室系统作为一款领先的智慧教育解决方案&#…...
)
OSCP-课外1(http万能密码、hydra密码暴力破解http、代码审计、Win缓存区溢出)
目录 难度 主机发现&端口扫描 信息收集 万能密码 hydra密码暴力破解...

ELK日志分析--Logstash
Logstash简介 Logstash安装 测试运行 配置输入和输出 使用Geoip过滤器插件增强数据编辑 配置接收 Beats 的输入 1.Logstash简介 Logstash管道具有两个必需元素input和output,以及一个可选元素filter。输入插件使用来自源的数据,过滤器插件根据你的…...
Mysql插入数据从指定选项中随机选择、插入时间从指定范围随机生成、Navicat使用存储过程模拟插入测试数据
场景 Navicat通过存储过程批量插入mysql数据: Navicat通过存储过程批量插入mysql数据_霸道流氓气质的博客-CSDN博客 上面使用过Navicat借助存储过程批量插入数据。但是插入数据是固定的 insert语句,如果在本地开发时需要模拟插入一些随机数据(从指定…...

【基础算法】关于高精度计算的问题【很高位数数据的加减乘除(相关代码用C++实现)】
文章目录前言1.高精度加法2.高精度减法3.高精度乘法4.高精度除法写在最后前言 当我们在利用计算机进行一些计算时,可能会遇到这类问题 : 有些计算要求精度高,希望计算的数的位数可达几十位甚至几百位,虽然计算机的计算精度也算较…...
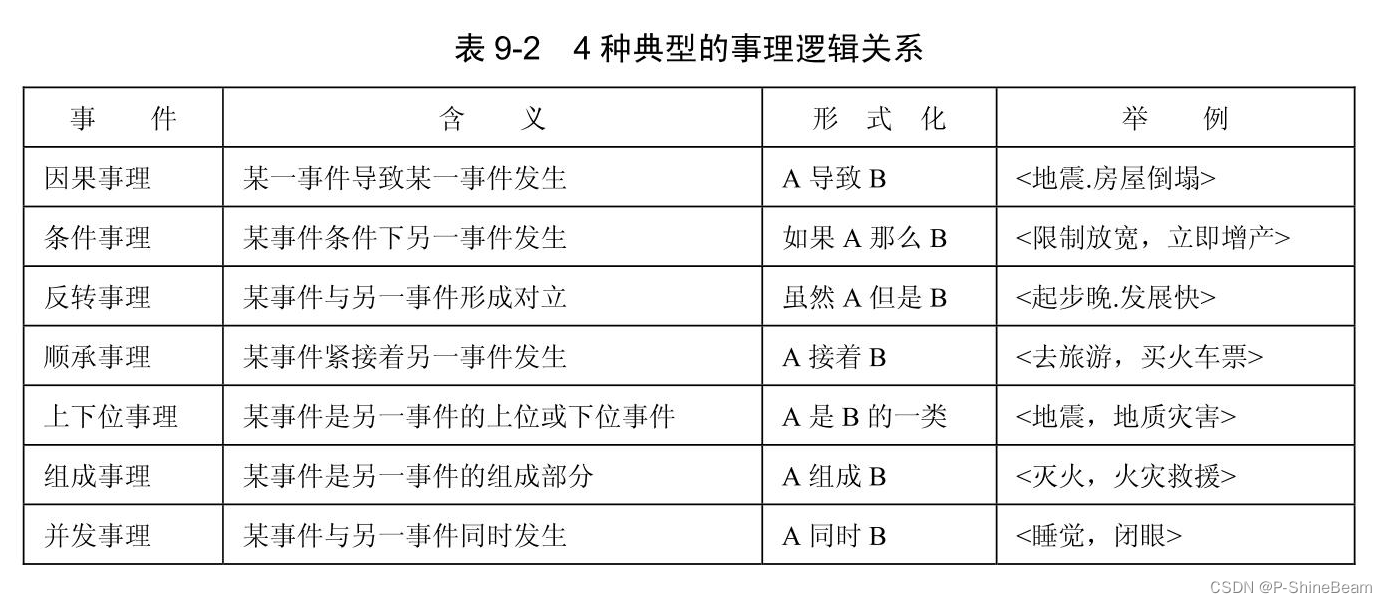
事理知识图谱
事理知识图谱能够有力第建模各类事件之间的演化关联关系为事理逻辑推理提供更好的数据基础。 事理图谱定义 事理知识图谱可以将文本中对事件以及事件之间的关系抽取并抽象出来,构建成一个有向图形式的事理知识库。在结构上,事理知识图谱是一个有向有环…...

多綫程之python爬蟲構建
目录多綫程定義簡介原理优点缺点优势代碼框架實現導包打印類爬蟲類構造方法獲取代理設置headers獲取新session獲取源代碼解析網頁解析子頁面保存數據綫程任務得到url啓動多綫程爬蟲總結多綫程 以下定義來自百度百科,看看就好沒仔細寫 定義 多线程(mul…...

【干货】Redis在Java开发中的基本使用和巧妙用法
Redis是一款高性能的内存数据结构存储系统,能够支持多种数据结构类型,如字符串、哈希、列表、集合、有序集合等,也能够支持高级功能,如事务、发布/订阅、Lua脚本等,具有高可用性、高并发性和可扩展性的优点。在Java开发…...

历时半年,我终于阿里上岸了,附面经和Java非科班学习心得
个人经历 本科双非化学,跨考了电子硕士,研究生依然双非。无互联网实习,无比赛无论文。(研究生研究方向是车辆电子和楼宇自动化,有自动化和高校实训讲师相关的实习经历) 21年11开始学Java准备秋招。 阿里上…...

ArkUI实战,自定义饼状图组件PieChart
本节笔者带领读者实现一个饼状图 PieChart 组件,该组件是根据笔者之前封装的 MiniCanvas 实现的, PieChart 的最终演示效果如下图所示: 饼状图实现的拆分 根据上图的样式效果,实现一个饼状图,实质就是绘制一个个的实…...
工作实战之系统交互api调用认证设计
目录 前言 一、黄金段位接口交互 二、钻石段位接口交互设计 1.接口文档定义 2.工具类以及demo提供 a.调用方部分代码 b.被调用方 三.星耀段位接口访问设计 1.在钻石段位的基础上,进行sdk的封装 a.maven引入 b.sdk包含工具类 四.王者段位接口访问设计 1.开发详情 2.…...

学习系统编程No.5【虚拟地址空间】
引言: 北京时间:2023/2/22,离补考期末考试还有5天,不慌,刚午觉睡醒,闹钟2点20,拖到2点50,是近以来,唯一一次有一种睡不醒的感觉,但是现在却没有精神,因为听了…...
)
Linux常用指令(未完待续。。。)
* basename:只留下路径的“最后一部分” X、文件夹&目录操作 复制 :cp /xxx /xxx - a 该选项通常在拷贝目录时使用。它保留链接、文件属性,并递归地拷贝目录,其作用等于dpR选项的组合; - d 拷贝时保留链接&#…...

用D写裸机
原文 用D编写裸机RISC-V应用 这篇文章展示,如何用D编写,目标为RISC-VQEMU模拟器的程序裸机"你好".项目 为什么是D? 我最近一直在用C编写裸机代码,我有点对C缺乏特征感到沮丧.D引入了叫betterC的模式(基本上禁止了D运行时的所有语言功能).使得D裸机编程大致与C一…...

(二十五)、实现评论功能(5)【uniapp+uinicloud多用户社区博客实战项目(完整开发文档-从零到完整项目)】
1,实现二级回复的入库操作 1.1 两个子组件(comment-item和comment-frame)与父组件reply之间的属性传值 comment-item: props: {item: {type: Object,default () {return {}}}},comment-frame: props: {commentObj: {…...
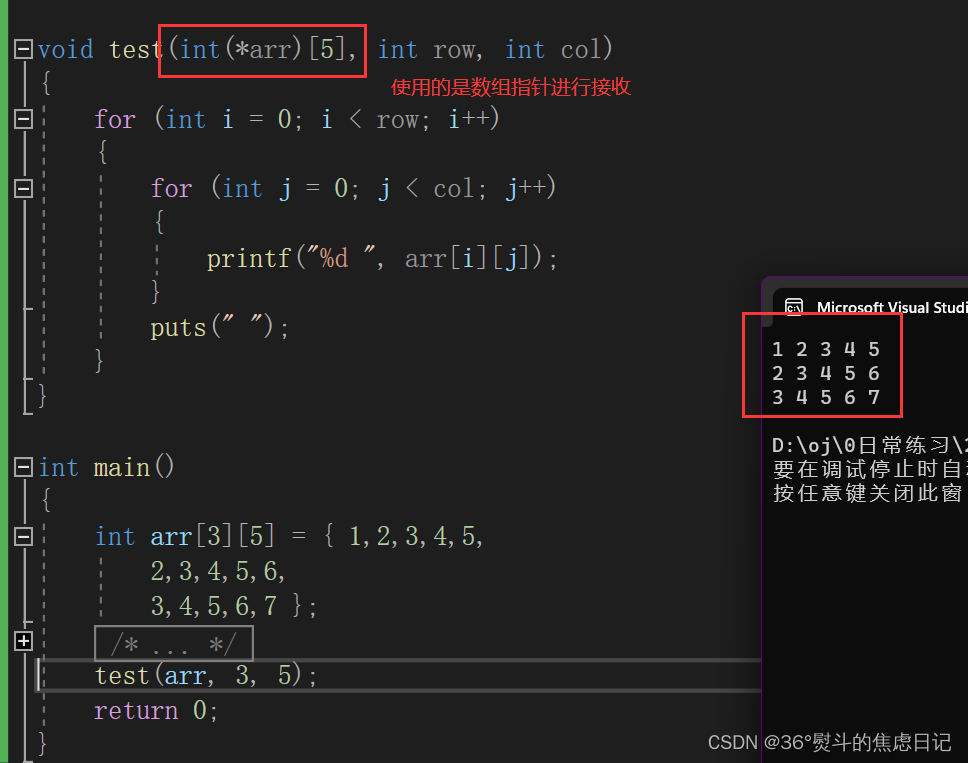
【概念辨析】二维数组传参的几种可能性
一、二维数组传参竟然不是用二级指针进行接收? 今天进行再一次的二级指针学习时,发现了一条以前没怎么注意过的知识点:二维数组进行传参只能用二维数组(不能省略列)进行接收或者是数组指针。 问题复现代码如下…...
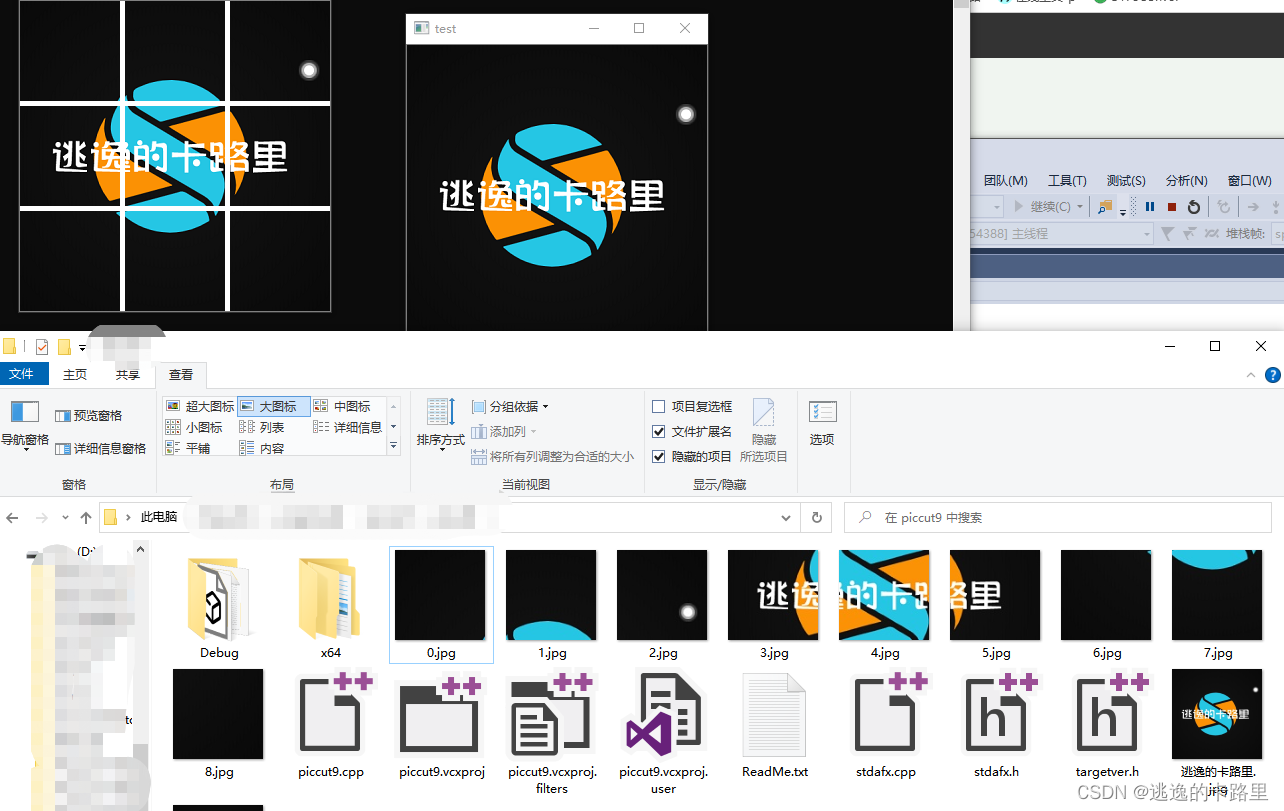
python和C++代码实现图片九宫格切图程序(附VS2015配置Opencv教程)
1、python代码实现图片分割成九宫格 需要包含的库,没有下载安装的,需要自己安装哦。 实现原理很简单,就是用PIL库不断画小区域,切下来存储成新的小图片。 假设每一个格子的宽和高分别是w、h,那么第row行(…...
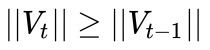
【深度学习】优化器
1.什么是优化器 优化器是在深度学习的反向传播过程中,指引损失函数(目标函数)的各个参数往正确的方向更新合适的大小,使得更新后的各个参数让目标函数不断逼近全局最小点。 2.优化器 2-1 BGD 批量梯度下降法,是梯度下…...
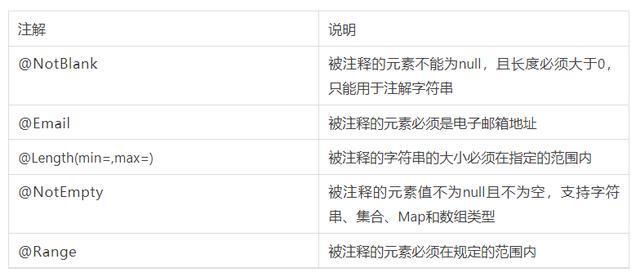
SpringBoot使用validator进行参数校验
Validated、Valid和BindingResultBean Validation是Java定义的一套基于注解的数据校验规范,比如Null、NotNull、Pattern等,它们位于 javax.validation.constraints这个包下。hibernate validator是对这个规范的实现,并增加了一些其他校验注解…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...

在树莓派上添加音频输入设备的几种方法
在树莓派上添加音频输入设备可以通过以下步骤完成,具体方法取决于设备类型(如USB麦克风、3.5mm接口麦克风或HDMI音频输入)。以下是详细指南: 1. 连接音频输入设备 USB麦克风/声卡:直接插入树莓派的USB接口。3.5mm麦克…...

DAY 26 函数专题1
函数定义与参数知识点回顾:1. 函数的定义2. 变量作用域:局部变量和全局变量3. 函数的参数类型:位置参数、默认参数、不定参数4. 传递参数的手段:关键词参数5 题目1:计算圆的面积 任务: 编写一…...

JS红宝书笔记 - 3.3 变量
要定义变量,可以使用var操作符,后跟变量名 ES实现变量初始化,因此可以同时定义变量并设置它的值 使用var操作符定义的变量会成为包含它的函数的局部变量。 在函数内定义变量时省略var操作符,可以创建一个全局变量 如果需要定义…...
