2023 ICPC 网络赛 第一场 部分题解 (待完善)
D Transitivity
题解:
根据题意可以推出结论: 如果存在连通块,那么这个连通块要满足条件,必然是满连通块.
一共有两种情况
1. 存在一个连通块不是满连通块
设cnt表示连通块的节点个数, num表示连通块边的个数
一个连通块的贡献 = cnt*(cnt-1)/2 - num;
那么最终答案 = 连通块贡献之和
2.所有连通块都是满连通块
因为我们至少需要添加一条边,所以此时等价于我们需要把两个连通块合并.
假设连通块A有x个节点,连通块B有y个节点,那么我们需要添加 x*y条边 才能满足条件.
所以即找到 最小和次小的连通块即可,答案 = x*y
AC代码:
#include <bits/stdc++.h>
typedef long long ll;
typedef unsigned long long ull;
#define int long long
#define endl '\n'
#define bit(x) (1ll << x)
using namespace std;
const int N = 1e6 + 5;
const int inf = 1e16;
vector<int> g[N];
int sz[N];//连通块大小
int cnt[N];//边的数量
int vis[N];
void solve()
{int n,m;cin >> n >> m;for(int i = 1; i<=m; i++){int u,v;cin >> u >> v;g[u].push_back(v);g[v].push_back(u);}int Min1 = inf;//最小值int Min2 = inf;//次小auto dfs = [&](auto self, int u, int fa,int root)-> void{vis[u] = 1;sz[u] = 1;cnt[root]+=g[u].size();for(auto v: g[u]){if(vis[v]){continue;}self(self,v,u,root);sz[u]+=sz[v];}};auto cal = [&](int now, int sum)//计算贡献{return sum*(sum-1)/2 - now;};int ans = 0;int f = 0;for(int i = 1; i<=n; i++){if(vis[i]){continue;}dfs(dfs,i,-1,i);cnt[i]/=2;int val = cal(cnt[i],sz[i]);//连通块的贡献if(val != 0){ans+=val;f = 1;}else{if(sz[i] < Min1){Min2 = Min1;Min1 = sz[i];}else if(sz[i] <=Min2){Min2 = sz[i];}}}if(f){cout << ans << endl;}else{cout << Min1*Min2 << endl;}
}signed main()
{ios_base::sync_with_stdio(0);cin.tie(0);cout.tie(0);int t = 1;//cin >> t;while (t--){solve();}return 0;
}A Qualifiers Ranking Rules
题解:
按照题意模拟即可
#include <bits/stdc++.h>
typedef long long ll;
typedef unsigned long long ull;
#define int long long
#define endl '\n'
#define bit(x) (1ll << x)
using namespace std;
const int N = 1e6 + 5;
const int inf = 1e16;
struct node
{string s; // 学校名称int rank; // 比赛名次int t;node(string x, int y, int _t){s = x;rank = y;t = _t;}
};
int cmp(node a, node b)
{if (a.rank == b.rank){return a.t < b.t;}return a.rank < b.rank;
}
void solve()
{int n, t;cin >> n >> t;map<string, int> vis;vector<node> pos1;int cnt = 1;for (int i = 1; i <= n; i++){string s;cin >> s;if (vis.count(s)){continue;}pos1.push_back({s, cnt, 1});vis[s] = 1;cnt++;}cnt = 1;vis.clear();for (int i = 1; i <= t; i++){string s;cin >> s;if (vis.count(s)){continue;}pos1.push_back({s, cnt, 2});cnt++;vis[s] = 1;}vis.clear();sort(pos1.begin(), pos1.end(), cmp);for (int i = 0; i < pos1.size(); i++){if (vis.count(pos1[i].s)){continue;}cout << pos1[i].s << endl;vis[pos1[i].s] = 1;}
}
signed main()
{ios_base::sync_with_stdio(0);cin.tie(0);cout.tie(0);int t = 1;// cin >> t;while (t--){solve();}return 0;
}L KaChang!
题解: 找到最大的数Max,输出 max(2ll,(int)ceil(1.0*Max/k)) 即可
void solve()
{int n,k;cin >> n >> k;int Max = 0;for(int i = 1; i<=n; i++){int x;cin >> x;Max = max(Max,x);}cout << max(2ll,(int)ceil(1.0*Max/k)) << endl;;
}I Pa?sWorD
题解:
设dp[i][S][ch] 表示只看前i个字母,且当前字符的出现状态为S,且最后一个字母是ch的方案数
(下面这些事伪代码,看不懂的可以直接看代码,有详细注释)
1.当前是 大写字母
dp[i][S| bit(2)][ch1] += dp[i-1][S][ch2];//其中ch2 != ch1 即上一层所有字符的方案数 - 上一层ch1的方案数
1.当前是 小写字母
(1)大写字母
dp[i][S| bit(2)][ch1] += dp[i-1][S][ch2];//其中ch2 != ch1 即上一层所有字符的方案数 - ch1的方案数
(2)填小写字母
dp[i][S| bit(1)][ch1] += dp[i-1][S][ch2];//其中ch2 != ch1 即上一层所有字符的方案数 - ch1的方案数
1.当前是 数字
dp[i][S| bit(0)][ch1] += dp[i-1][S][ch2];//其中ch2 != ch1 即上一层所有字符的方案数 - ch1的方案数
1.当前是 问号
枚举当前字符ch1, t表示当前字母是谁
dp[i][S| bit(t)][ch1] += dp[i-1][S][ch1];//其中ch2 != ch1 即上一层所有字符的方案数 - ch1的方案数
AC代码:
#include <bits/stdc++.h>
typedef long long ll;
typedef unsigned long long ull;
#define int long long
#define endl '\n'
#define bit(x) (1ll << x)
using namespace std;
const int N = 1e6 + 5;
const int inf = 1e16;
const int MOD = 998244353;
int add(int x, int y)
{x += y;while (x >= MOD)x -= MOD;while (x < 0)x += MOD;return x;
}int sub(int x, int y)
{return add(x, MOD - y);
}int mul(int x, int y)
{return (x * 1ll * y) % MOD;
}int binpow(int x, int y)
{int z = 1;while (y > 0){if (y % 2 == 1)z = mul(z, x);x = mul(x, x);y /= 2;}return z;
}int inv(int x)
{return binpow(x, MOD - 2);
}int divide(int x, int y)
{return mul(x, inv(y));
}int my_hash(char ch)//对字符进行哈希
{if (ch >= 'a' && ch <= 'z'){return ch - 'a' + 10;}else if (ch >= 'A' && ch <= 'Z'){return ch - 'A' + 36;}else{return ch - '0';}
}
int pos(int ch)//当前字符在二进制中的位置
{if (ch >= 10 && ch <= 35) // 小写表示第1位{return 1;}else if (ch >= 36 && ch <= 61) // 大写表示第2位{return 2;}else // 数字表示第0位{return 0;}
}int dp[2][10][70]; // 当前状态为S且最后一个字符是 ch 的方案数
int last[10]; // 状态为S时 所有的字符方案数之和
void solve()
{int n;cin >> n;string s;cin >> s;s = " " + s;//初始化部分int S = 0;int now;int ch; // 当前填入的字符编号if (s[1] == '?'){for (ch = 0; ch <= 61; ch++) // 当前填入ch{now = S | bit(pos(ch)); // 填入s[i]后,当前的二进制状态dp[1][now][ch] = 1;}}else{now = S | bit(pos(my_hash(s[1]))); // 填入s[i]后,当前的二进制状态ch = my_hash(s[1]);dp[1][now][ch] = 1; // 加上全部的if (s[1] >= 'a' && s[1] <= 'z')//如果是小写字母,还可以是大写字母{now = S | bit(pos(my_hash(s[1]) + 26)); // 填入s[i]后,当前的二进制状态ch = my_hash(s[1]) + 26; // 填大写字母dp[1][now][ch] = 1; // 加上全部的}}for (int i = 2; i <= n; i++){for (int S = 0; S < 8; S++)//{int sum = 0;for (int ch = 0; ch <= 61; ch++){dp[0][S][ch] = dp[1][S][ch]; // 滚动数组dp[1][S][ch] = 0; // 进行初始化sum = add(sum, dp[0][S][ch]);//表示上一层状态为S的所有字符的方案数}last[S] = sum; // 表示上一层状态为S的所有字符的方案数}for (int S = 0; S < 8; S++) // 枚举上一层的状态{int now;//表示填入字符后的状态int ch; // 当前填入的字符编号if (s[i] == '?'){for (ch = 0; ch <= 61; ch++) // 当前填入ch{now = S | bit(pos(ch)); // 填入s[i]后,当前的二进制状态dp[1][now][ch] = add(dp[1][now][ch], last[S]); // 加上全部的dp[1][now][ch] = sub(dp[1][now][ch], dp[0][S][ch]); // 相邻不能相同,减去}}else{now = S | bit(pos(my_hash(s[i]))); // 填入s[i]后,当前的二进制状态ch = my_hash(s[i]);dp[1][now][ch] = add(dp[1][now][ch], last[S]); // 加上全部的dp[1][now][ch] = sub(dp[1][now][ch], dp[0][S][ch]); // 相邻不能相同,减去if (s[i] >= 'a' && s[i] <= 'z') // 填入大写的{now = S | bit(pos(my_hash(s[i]) + 26)); // 填入s[i]后,当前的二进制状态ch = my_hash(s[i]) + 26;dp[1][now][ch] = add(dp[1][now][ch], last[S]); // 加上全部的dp[1][now][ch] = sub(dp[1][now][ch], dp[0][S][ch]); // 相邻不能相同,减去}}}}int ans = 0;for (int ch = 0; ch <= 61; ch++){ans = add(ans, dp[1][7][ch]);}cout << ans << endl;
}
signed main()
{ios_base::sync_with_stdio(0);cin.tie(0);cout.tie(0);int t = 1;// cin >> t;while (t--){solve();}return 0;
}相关文章:
)
2023 ICPC 网络赛 第一场 部分题解 (待完善)
D Transitivity 题解: 根据题意可以推出结论: 如果存在连通块,那么这个连通块要满足条件,必然是满连通块. 一共有两种情况 1. 存在一个连通块不是满连通块 设cnt表示连通块的节点个数, num表示连通块边的个数 一个连通块的贡献 cnt*(cnt-1)/2 - num; 那么最终答案 连…...

Hadoop的HDFS高可用方案
一、Hadoop高可用简介 Hadoop 高可用 (High Availability) 分为 HDFS 高可用和 YARN 高可用,两者的实现基本类似,但 HDFSNameNode 对数据存储及其一致性的要求比 YARN ResourceManger 高得多,所以它的实现也更加复杂 1、HDFS系统高可用简介…...

【计算机基础】让我们重新认识一下Visual Stduio及其操作,知识点汇总!!
📢:如果你也对机器人、人工智能感兴趣,看来我们志同道合✨ 📢:不妨浏览一下我的博客主页【https://blog.csdn.net/weixin_51244852】 📢:文章若有幸对你有帮助,可点赞 👍…...

使用Node构建私人代理池
在进行大规模数据采集时,经常会遇到网站反爬虫机制导致爬虫被封的问题。为了解决这个困扰,本文将向大家介绍如何利用Node.js构建私人代理池,提供稳定的代理,实现高效、可靠的爬虫操作。跟随本文一起学习,拥有解封爬虫的…...

2023年“羊城杯”网络安全大赛 决赛 AWDP [Break+Fix] Web方向题解wp 全
终于迎来了我的第一百篇文章。 这次决赛赛制是AWDP。BreakFix,其实就是CTFFix,Fix规则有点难崩。Break和Fix题目是一样的。 总结一下:败北,还是太菜了得继续修炼一下。 一、Break ezSSTI 看到是SSTI,焚靖直接一把梭…...
如何用好免费的ChatGPT
如何用好免费的ChatGPT 前言ChatGPT使用入口在线体验地址:点我体验 ChatGPT介绍ChatGPT初级使用技巧初级使用技巧:清晰明了的问题表达 ChatGPT中级使用语法中级使用语法:具体化问题并提供背景信息 ChatGPT高级使用高级使用:追问、…...

golang 实现带令牌限流的JWT demo
demo里提供了三个接口,认证取token,刷新token,获取信息,token过期前也会在header里写上新token(便于客户端更换) package mainimport ("fmt""net/http""sync""time&qu…...
ajax请求)
【web开发】9、Django(4)ajax请求
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 一、Ajax是什么?二、使用步骤二、订单管理 提示:以下是本篇文章正文内容,下面案例可供参考 一、Ajax是什么? Ajax&…...
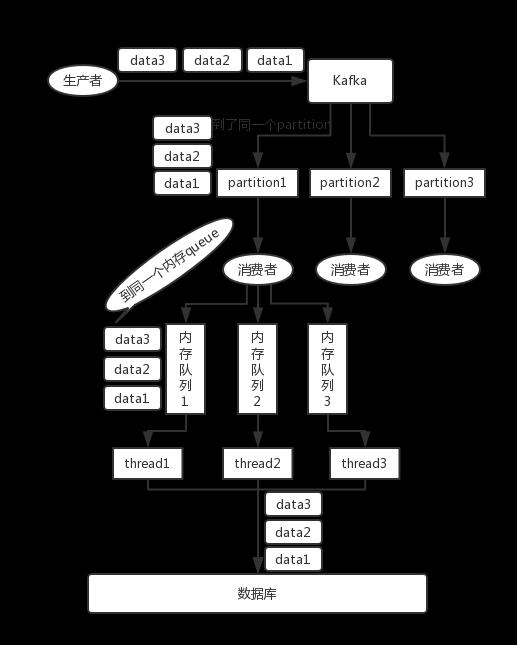
消息队列中,如何保证消息的顺序性?
本文选自:advanced-java 作者:yanglbme 问:如何保证消息的顺序性? 面试官心理分析 其实这个也是用 MQ 的时候必问的话题,第一看看你了不了解顺序这个事儿?第二看看你有没有办法保证消息是有顺序的…...

Shell别名的使用方法及管理技巧
文章目录 1. 引言1.1 概述1.2 目的1.3 适用范围 2. Shell和别名2.1 Shell简介2.2 别名的作用2.3 别名的语法 3. 创建别名3.1 临时别名3.2 永久别名 4. 别名的应用4.1 简化命令4.2 自定义命令4.3 提高工作效率 5. 管理别名5.1 查看别名5.2 修改别名5.3 删除别名 6. 实例演示6.1 …...

C/C++选择题好题分享
...
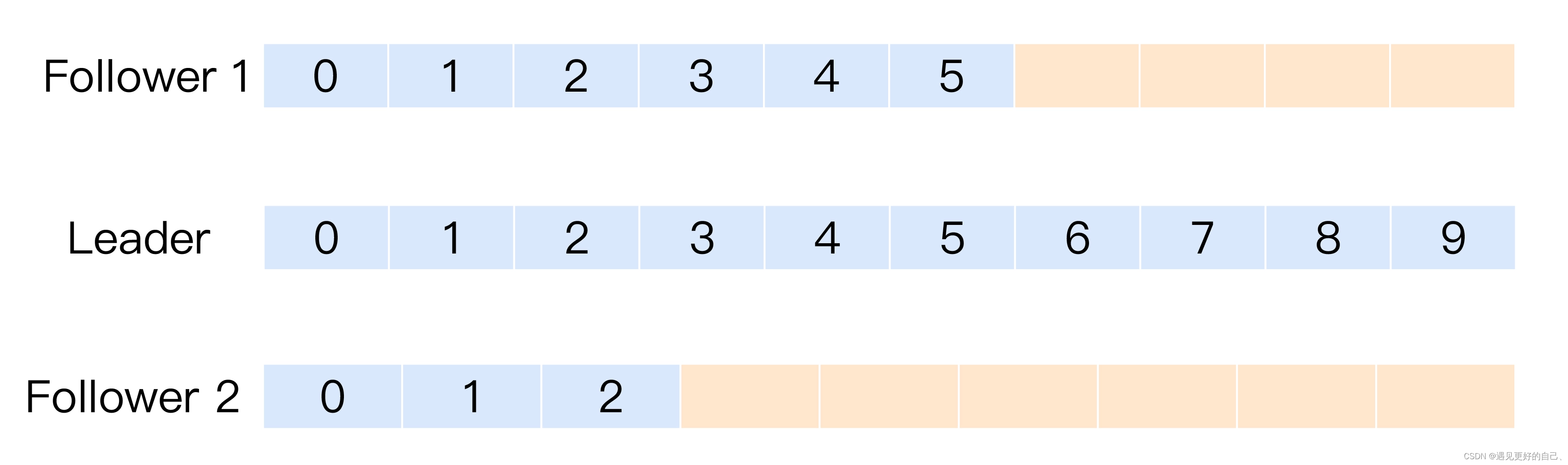
kafka副本机制
目录 前言 副本定义 副本角色 In-sync Replicas(ISR) 参考资料 前言 现在的很多的分布式系统都支持副本的机制,比如Mysql就有副本的机制,一般使用副本有如下特性和好处。 提供数据冗余。即使系统部分组件失效,系…...

服务注册发现_actuator微服务信息完善
SpringCloud体系里的,服务实体向eureka注册时,注册名默认是IP名:应用名:应用端口名。 问题: 自定义服务在Eureka上的实例名怎么弄呢 在服务提供者pom中配置Actuator依赖 <!-- actuator监控信息完善 --> <dependency><groupId…...

常见列表字典排序
一、列表排序 demoList [1, 3, 2, 4, 9 ,7]res sorted(demoList) # 默认升序# 降序 # res sorted(demoList, reverseTrue)print(res)二、字典排序 demoDict {"篮球": 5, "排球": 9, "网球": 6, "足球": 3}# sorted排序 res so…...
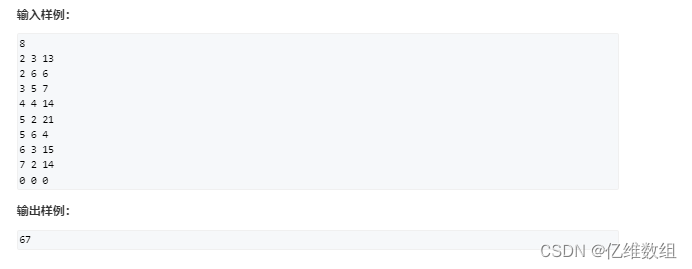
【Acwing1027】方格取数(动态规划)题解
题目描述 思路分析 错误思路: 贪心法,先走一次求出最大值,把走过的路上面的数值清零,然后用同样的方法再走一遍求最大值,然后让这两个最大值相加就是最后的结果。 很多人在看到这个题目的时候会有上面的思路&#x…...

合并区间:解决区间重叠问题的高效算法
合并区间:解决区间重叠问题的高效算法 leetcode 56. 合并区间 合并区间是一个常见的编程问题,通常涉及到一组区间,你需要将重叠的区间合并成更大的区间。这篇博客将介绍这个问题的背景,然后解释一个高效的解决方案,同…...

万字总结HTML超文本标记语言
一、前言:什么是网页? 网站是指在因特网上根据一定的规则,使用 HTML 等制作的用于展示特定内容相关的网页集合。网页是网站中的一“页”,通常是 HTML 格式的文件,它要通过浏览器来阅读。 网页是构成网站的基本元素,它通常由图片、链接、文字、声音、视频等元素组成。通常…...
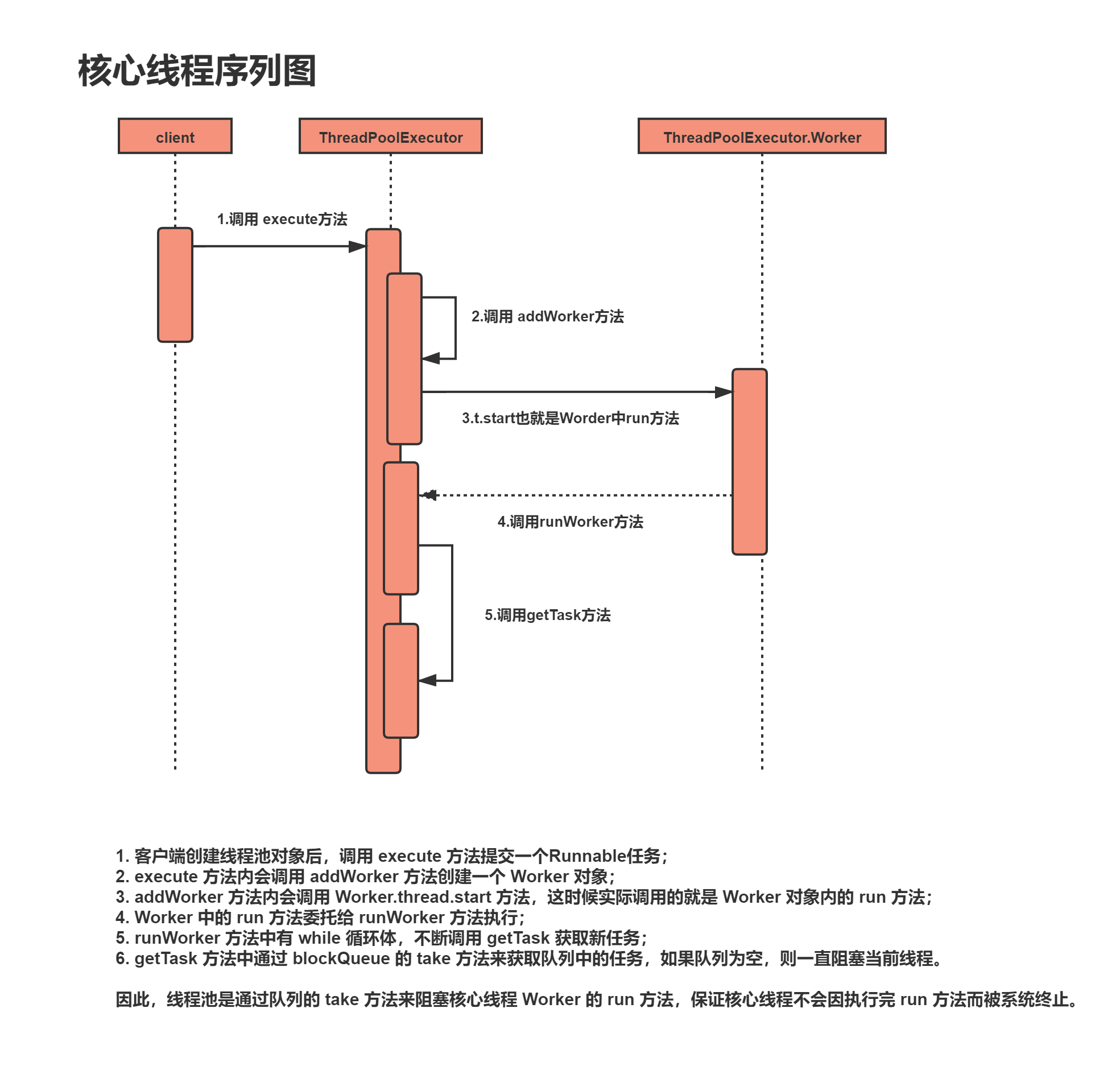
Java线程池是如何保证核心线程不被销毁的
来源: Java线程池是如何保证核心线程不被销毁的_朝 花 拾 夕的博客-CSDN博客 对于Java中 Thread 对象,同一个线程对象调用 start 方法后,会在执行完run 后走向终止(TERMINATED)状态,也就是说一个线程对象是不可以通过多…...

新课程标准培养学生“高考物理关键能力”的实践研究课题文献综述
目录 一、高考物理能力的要求与评估标准 二、高考物理关键能力的定义与内涵...

急救车工业路由器应用提升急救效率:车联网、数据采集与远程诊疗
急救车作为医院里医疗急救过程中的重要组成部分,在智慧医疗物联网领域中急救车应用4G工业路由器实现网络部署与数据采集,通过工业4G路由器能够实时采集到病患的生理数据、救护现场音频与视频、GPS定位以及车辆运行状态等重要信息。这些数据将被传输到医疗…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

GruntJS-前端自动化任务运行器从入门到实战
Grunt 完全指南:从入门到实战 一、Grunt 是什么? Grunt是一个基于 Node.js 的前端自动化任务运行器,主要用于自动化执行项目开发中重复性高的任务,例如文件压缩、代码编译、语法检查、单元测试、文件合并等。通过配置简洁的任务…...

STM32---外部32.768K晶振(LSE)无法起振问题
晶振是否起振主要就检查两个1、晶振与MCU是否兼容;2、晶振的负载电容是否匹配 目录 一、判断晶振与MCU是否兼容 二、判断负载电容是否匹配 1. 晶振负载电容(CL)与匹配电容(CL1、CL2)的关系 2. 如何选择 CL1 和 CL…...

MyBatis中关于缓存的理解
MyBatis缓存 MyBatis系统当中默认定义两级缓存:一级缓存、二级缓存 默认情况下,只有一级缓存开启(sqlSession级别的缓存)二级缓存需要手动开启配置,需要局域namespace级别的缓存 一级缓存(本地缓存&#…...

学习一下用鸿蒙DevEco Studio HarmonyOS5实现百度地图
在鸿蒙(HarmonyOS5)中集成百度地图,可以通过以下步骤和技术方案实现。结合鸿蒙的分布式能力和百度地图的API,可以构建跨设备的定位、导航和地图展示功能。 1. 鸿蒙环境准备 开发工具:下载安装 De…...

Python 训练营打卡 Day 47
注意力热力图可视化 在day 46代码的基础上,对比不同卷积层热力图可视化的结果 import torch import torch.nn as nn import torch.optim as optim from torchvision import datasets, transforms from torch.utils.data import DataLoader import matplotlib.pypl…...

AD学习(3)
1 PCB封装元素组成及简单的PCB封装创建 封装的组成部分: (1)PCB焊盘:表层的铜 ,top层的铜 (2)管脚序号:用来关联原理图中的管脚的序号,原理图的序号需要和PCB封装一一…...
