九、多项式朴素贝叶斯算法(Multinomial NB,Multinomial Naive Bayes)(有监督学习)
Multinomial Naive Bayes:用于多项式模型的Naive Bayes分类器
一、算法思路
多项式Naive Bayes分类器适用于离散特征分类(如文本分类中的字数)
多叉分布通常需要整数特征计数
不过,在实际应用中,分数计数(如 tf-idf)也可以起作用
二、官网API
官网API
导包:from sklearn.naive_bayes import MultinomialNB
class sklearn.naive_bayes.MultinomialNB(*, alpha=1.0, force_alpha='warn', fit_prior=True, class_prior=None)
①平滑参数alpha
加法(拉普拉斯/利德斯通)平滑参数(设置 alpha=0 和 force_alpha=True 表示不平滑)
浮点数,默认为1.0
也可以传入array形式,array为各个特征值
具体官网详情如下:

使用方法
MultinomialNB(alpha=1.2)
或者
beyond = ['cat','dog']
multinomial = MultinomialNB(alpha=beyond)
②force_alpha
如果为False,且alpha小于1e-10,则会将alpha设置为1e-10,默认值
如果为True,alpha将保持不变
如果alpha太接近0,可能会导致数字错误
具体官网详情如下:

使用方法
MultinomialNB(force_alpha=True)
③fit_prior
是否学习类别先验概率。如果为False,将使用统一先验;默认值为True
具体官网详情如下:

使用方法
MultinomialNB(fit_prior=False)
④类别先验概率class_prior
class_prior类别的先验概率;如果指定,则不会根据数据调整先验概率;默认值为None
具体官网详情如下:

使用方法
beyond = ['cat','dog']
multinomial = MultinomialNB(class_prior=beyond)
⑤最终构建模型
MultinomialNB(alpha=1.2,force_alpha=True,fit_prior=False)
三、代码实现
①导包
这里需要评估、训练、保存和加载模型,以下是一些必要的包,若导入过程报错,pip安装即可
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import joblib
%matplotlib inline
import seaborn as sns
from sklearn.preprocessing import LabelEncoder
from sklearn.model_selection import train_test_split
from sklearn.naive_bayes import MultinomialNB
from sklearn.metrics import confusion_matrix, classification_report, accuracy_score
②加载数据集
数据集可以自己简单整个,csv格式即可,我这里使用的是6个自变量X和1个因变量Y
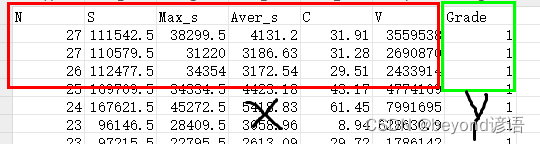
fiber = pd.read_csv("./fiber.csv")
fiber.head(5) #展示下头5条数据信息
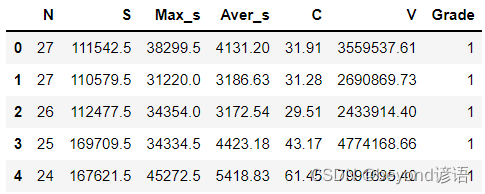
③划分数据集
前六列是自变量X,最后一列是因变量Y
常用的划分数据集函数官网API:train_test_split
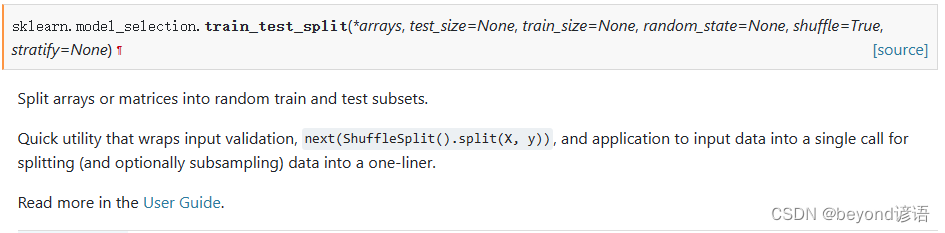
test_size:测试集数据所占比例
train_size:训练集数据所占比例
random_state:随机种子
shuffle:是否将数据进行打乱
因为我这里的数据集共48个,训练集0.75,测试集0.25,即训练集36个,测试集12个
X = fiber.drop(['Grade'], axis=1)
Y = fiber['Grade']X_train, X_test, y_train, y_test = train_test_split(X,Y,train_size=0.75,test_size=0.25,random_state=42,shuffle=True)print(X_train.shape) #(36,6)
print(y_train.shape) #(36,)
print(X_test.shape) #(12,6)
print(y_test.shape) #(12,)
④构建MultinomialNB模型
参数可以自己去尝试设置调整
multinomial = MultinomialNB(alpha=1.2,force_alpha=True,fit_prior=False)
⑤模型训练
就这么简单,一个fit函数就可以实现模型训练
multinomial.fit(X_train,y_train)
⑥模型评估
把测试集扔进去,得到预测的测试结果
y_pred = multinomial.predict(X_test)
看看预测结果和实际测试集结果是否一致,一致为1否则为0,取个平均值就是准确率
accuracy = np.mean(y_pred==y_test)
print(accuracy)
也可以通过score得分进行评估,计算的结果和思路都是一样的,都是看所有的数据集中模型猜对的概率,只不过这个score函数已经封装好了,当然传入的参数也不一样,需要导入accuracy_score才行,from sklearn.metrics import accuracy_score
score = multinomial.score(X_test,y_test)#得分
print(score)
⑦模型测试
拿到一条数据,使用训练好的模型进行评估
这里是六个自变量,我这里随机整个test = np.array([[16,18312.5,6614.5,2842.31,25.23,1147430.19]])
扔到模型里面得到预测结果,prediction = multinomial.predict(test)
看下预测结果是多少,是否和正确结果相同,print(prediction)
test = np.array([[16,18312.5,6614.5,2842.31,25.23,1147430.19]])
prediction = multinomial.predict(test)
print(prediction) #[2]
⑧保存模型
multinomial是模型名称,需要对应一致
后面的参数是保存模型的路径
joblib.dump(multinomial, './multinomial.model')#保存模型
⑨加载和使用模型
multinomial_yy = joblib.load('./multinomial.model')test = np.array([[11,99498,5369,9045.27,28.47,3827588.56]])#随便找的一条数据
prediction = multinomial_yy.predict(test)#带入数据,预测一下
print(prediction) #[4]
完整代码
模型训练和评估,不包含⑧⑨。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import joblib
%matplotlib inline
import seaborn as sns
from sklearn.preprocessing import LabelEncoder
from sklearn.model_selection import train_test_split
from sklearn.naive_bayes import MultinomialNB
from sklearn.metrics import confusion_matrix, classification_report, accuracy_scorefiber = pd.read_csv("./fiber.csv")
fiber.head(5) #展示下头5条数据信息X = fiber.drop(['Grade'], axis=1)
Y = fiber['Grade']X_train, X_test, y_train, y_test = train_test_split(X,Y,train_size=0.75,test_size=0.25,random_state=42,shuffle=True)print(X_train.shape) #(36,6)
print(y_train.shape) #(36,)
print(X_test.shape) #(12,6)
print(y_test.shape) #(12,)multinomial= MultinomialNB(alpha=1.2,force_alpha=True,fit_prior=False)
multinomial.fit(X_train,y_train)y_pred = multinomial.predict(X_test)
accuracy = np.mean(y_pred==y_test)
print(accuracy)
score = multinomial.score(X_test,y_test)#得分
print(score)test = np.array([[16,18312.5,6614.5,2842.31,25.23,1147430.19]])
prediction = multinomial.predict(test)
print(prediction) #[2]
相关文章:

九、多项式朴素贝叶斯算法(Multinomial NB,Multinomial Naive Bayes)(有监督学习)
Multinomial Naive Bayes:用于多项式模型的Naive Bayes分类器 一、算法思路 多项式Naive Bayes分类器适用于离散特征分类(如文本分类中的字数) 多叉分布通常需要整数特征计数 不过,在实际应用中,分数计数(…...
数据结构上机练习——单链表的基本操作、头文件、类定义、main函数、多种链表算法的实现,含注释
文章目录 单链表的基本操作实现1.头文件2.类定义和多种算法的实现2.1创建空表2.2头插法创建n个元素的线性链表2.3一个带头节点的链表存放一组整数,设计一个算法删除值等于x的所有节点。2.4计算线性表中值为偶数的节点个数2.5一个带头节点的单链表heada存放一组整数&…...

如何通过AI视频智能分析技术,构建着装规范检测/工装穿戴检测系统?
众所周知,规范着装在很多场景中起着重要的作用。违规着装极易增加安全隐患,并且引发安全事故和质量问题,例如,在化工工厂中,倘若员工没有穿戴符合要求的特殊防护服和安全鞋,将有极大可能受到有害物质的侵害…...
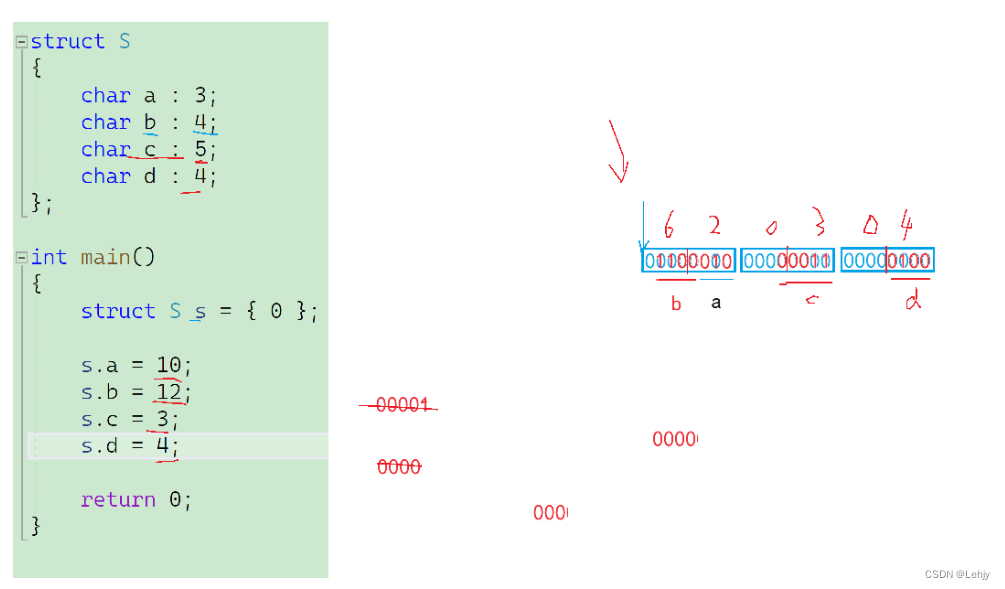
C语言自定义类型(上)
大家好,我们又见面了,这一次我们来学习一些C语言有关于自定义类型的结构。 目录 1.结构体 2位段 1.结构体 前面我们已经学习了一些有关于结构体的知识,现在我们进行深入的学习有关于它的知识。 结构是一些值的集合,这些值称为…...

Python - 小玩意 - 圣诞树背景音乐弹窗
import turtle as t import tkinter as tk import pygame import random as r import threading import time# 初始化背景音乐 def initialize_music():file r"./music/周杰伦-蜗牛.mp3"pygame.mixer.init()pygame.mixer.music.load(file)pygame.mixer.music.play()…...

The 2023 ICPC Asia Regionals Online Contest (1) E. Magical Pair(数论 欧拉函数)
题目 T(T<10)组样例,每次给出一个n(2<n<1e18), 询问多少对,满足 答案对998244353取模,保证n-1不是998244353倍数 思路来源 OEIS、SSerxhs、官方题解 2023 ICPC 网络赛 第一场简要题解 - 知乎 题解 官方题解还没有…...

<十三>objectARX开发:模拟实现CAD的移动Move命令
一、目的 实现类似于CAD的移动命令,选择对象,移动到指定位置,移动过程中对象跟随鼠标移动。效果如下: 二、关键步骤 选择对象,打开实体判断类型:acedEntSel()、acdbOpenObject()、isKindOf()。指定基点:acedGetPoint()。移动模型,追踪光标移动对象实体:acedGrRead()…...

Autosar基础:模式管理-EcuM
ECUM目录 前言一、ECUM状态机二、Fixed和Flexible模式的区别与联系三、状态详解3.1.Startup3.2.UP3.3.RUN3.4.Sleep3.5.Shutdown三、EcuM唤醒源3.1 CAN Trcv唤醒3.2 唤醒后操作前言 根据Autosar对于模式管理的需求定义,模式管理有以下模块: ①ECU State Manager(EcuM):管理…...

代码随想录Day42 | 01背包问题| 416. 分割等和子集
01背包问题(Acwing) 有 N 件物品和一个容量是 V的背包。每件物品只能使用一次。 第 i 件物品的体积是 vi,价值是 wi。 求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。 输出最大价值。 输入…...
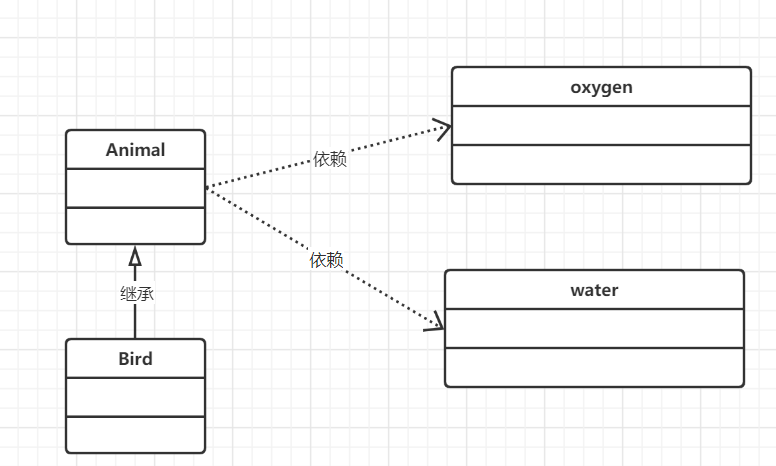
UML六大关系总结
UML六大关系有:继承、关系、聚合、组合、实现、依赖。分为通过图和代码总结这些关系。 1、继承 继承(Inheritance):表示类之间的继承关系,子类继承父类的属性和方法,并可以添加自己的扩展。 继承&#x…...

ElementUI基本介绍及登录注册案例演示
目录 前言 一.简介 二.优缺点 三.Element完成登录注册 1. 环境配置及前端演示 1.1 安装Element-UI模块 1.2 安装axios和qs(发送get请求和post请求) 1.3 导入依赖 2 页面布局 2.1组件与界面 3.方法实现功能数据交互 3.1 通过方法进行页面跳转 3.2 axios发送get请求 …...
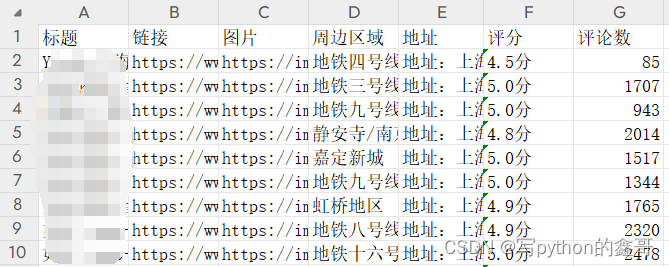
Python爬虫-某网酒店评论数据
前言 本文是该专栏的第6篇,后面会持续分享python爬虫案例干货,记得关注。 本文以某网的酒店数据为例,采集对应酒店的评论数据。具体思路和方法跟着笔者直接往下看正文详细内容。(附带完整代码) 注意:本文的案例“数据集”,选用的是本专栏上一篇“Python爬虫-某网酒店数…...
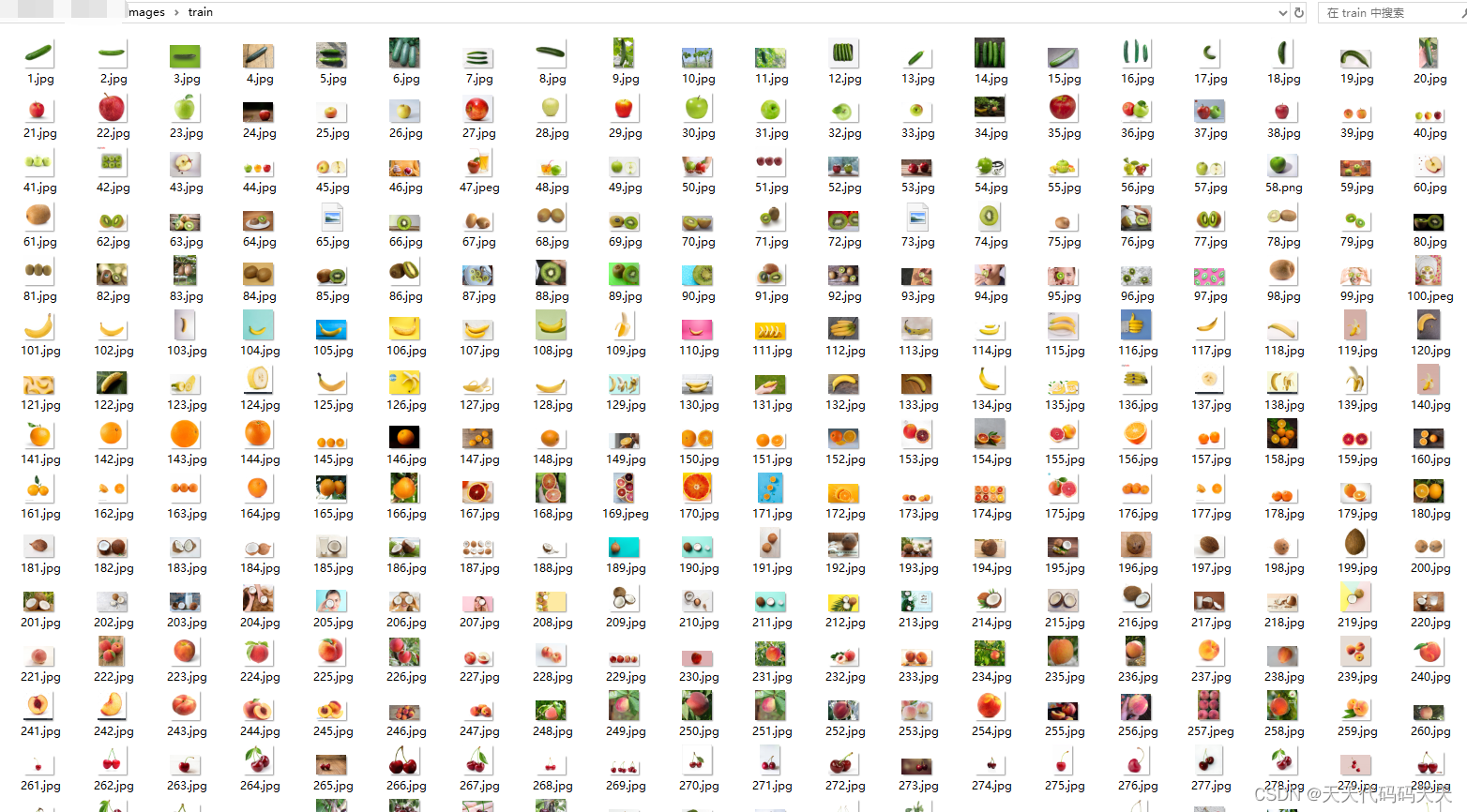
C# Onnx Yolov8 Detect 水果识别
效果 项目 代码 using Microsoft.ML.OnnxRuntime; using Microsoft.ML.OnnxRuntime.Tensors; using OpenCvSharp; using System; using System.Collections.Generic; using System.ComponentModel; using System.Data; using System.Drawing; using System.Linq; using System…...
测试网页调用本地可执行程序(续1:解析参数中的中文编码)
学习测试网页调用本地可执行程序还遗留一个问题,即网页中调用带中文参数的命令时,本地可执行程序接收到的参数字符串里的中文都转换成了编码模式,看起来如下所示: <a href TestPageCall:-a你好>启动测试程序</a><…...

C++入门知识
Hello,今天我们分享一些关于C入门的知识,看完至少让你为后面的类和对象有一定的基础,所以在讲类和对象的时候,我们需要来了解一些关于C入门的知识。 什么是C C语言是结构化和模块化的语言,适合处理较小规模的程序。对…...

spring和springmvc常用注解
1.Spring常用注解: 1)Repository将DAO类声明为Bean 2)Service用于修饰service层的组件 3)Controller通常作用在控制层,将在Spring MVC中使用 4)Component是一个泛化的概念,仅仅表示spring中的一…...

【Java】Java生成PDF工具类
Java生成PDF工具类 一、介绍 Java生成PDF工具类是一个非常实用的工具类,可以帮助我们以程序化的方式生成PDF文件。通过该工具类,我们可以向PDF文件中添加文字、图片、表格等多种内容,并且可以进行格式化和样式设置。Java生成PDF工具类常用于…...

STL map,插入和查找的一些注意事项
01、前言(废话) C 的 std::map 容器中插入键值对主要有myMap(std::make_pair(key value)) ,它们的区别你了解吗? auto it myMap,find(key) 和 auto value myMap[key] 都可以用于在 C 的 std::map 容器中查找键对应的值ÿ…...
基于springboot+vue的客户关系管理系统(前后端分离)
博主主页:猫头鹰源码 博主简介:Java领域优质创作者、CSDN博客专家、公司架构师、全网粉丝5万、专注Java技术领域和毕业设计项目实战 主要内容:毕业设计(Javaweb项目|小程序等)、简历模板、学习资料、面试题库、技术咨询 文末联系获取 项目介绍…...

【Java 基础篇】Java Stream 流详解
Java Stream(流)是Java 8引入的一个强大的新特性,用于处理集合数据。它提供了一种更简洁、更灵活的方式来操作数据,可以大大提高代码的可读性和可维护性。本文将详细介绍Java Stream流的概念、用法和一些常见操作。 什么是Stream…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...
