【数据结构】插入排序:直接插入排序、折半插入排序、希尔排序的学习知识总结
目录
1、排序的基本概念
2、直接插入排序
2.1 算法思想
2.2 代码实现
3、折半插入排序
3.1 算法思想
3.2 代码实现
4、希尔排序
4.1 算法思想
4..2 代码实现
1、排序的基本概念
排序是将一组数据按照预定的顺序排列的过程,排序的基本概念包括以下内容:
-
关键字:排序时按照哪个字段进行排序,该字段称为关键字。
-
排序规则:排序时按照升序或降序的方式排列。升序表示从小到大排列,降序表示从大到小排列。
-
稳定性:排序算法如果经过排序后,具有相同关键字的元素,排序前后的相对顺序是否保持不变。如果保持不变,该排序算法就是稳定的。
-
时间复杂度:排序算法进行排序所需要的时间复杂度。
-
空间复杂度:排序算法进行排序所需要的额外空间复杂度,即算法需要占用的额外内存大小。
2、直接插入排序
2.1 算法思想
直接插入排序算法的思想是将待排序的元素插入到已经排好序的元素序列中,从而得到一个新的、更大的有序序列。
具体来说,算法从第二个元素开始遍历待排序序列,将当前元素插入到已经排好的元素序列中的正确位置上,使得插入后仍然保持有序。因为初始时已经有一个元素的有序序列,所以排序过程中每次插入的元素都将比已经排好序的元素序列中的元素小,因此不会影响已经排好序的元素序列的有序性。当遍历完整个序列,待排序序列就被完全插入到已经排好序的元素序列中,排序完成。
直接插入排序的时间复杂度为O(n^2),空间复杂度为O(1)。虽然时间复杂度较高,但是对于小规模数据的排序效率较高,并且具有稳定性。
2.2 代码实现
以下是C语言编写的直接插入排序并计数比较次数的程序:
#include <stdio.h>
#define MAXSIZE 100void InsertionSort(int A[], int n, int *cnt) {int i, j, temp;for(i = 1; i < n; i++) {temp = A[i];for(j = i - 1; j >= 0; j--) {(*cnt)++;if(A[j] > temp)A[j + 1] = A[j];elsebreak;}A[j + 1] = temp;}
}int main() {int A[MAXSIZE];int n, cnt = 0;printf("请输入待排序数列元素个数(不超过%d):", MAXSIZE);scanf("%d", &n);printf("请输入待排序数列:");for(int i = 0; i < n; i++)scanf("%d", &A[i]);InsertionSort(A, n, &cnt);printf("排序后结果:");for(int i = 0; i < n; i++)printf("%d ", A[i]);printf("\n比较次数:%d\n", cnt);return 0;
}
程序中的 InsertionSort 函数实现了直接插入排序,并使用指针形参 cnt 对比较次数进行计数。主函数中首先输入待排序数列元素个数和数列元素,然后调用 InsertionSort 函数进行排序,并输出排序后的结果和比较次数。
下面是C语言在链式存储结构上设计直接插入排序算法的示例代码:
typedef struct Node {int data;struct Node *next;
}Node;void insertSort(Node **head) {if (*head == NULL || (*head)->next == NULL) {return;}Node *p = (*head)->next;(*head)->next = NULL; // 设置新的有序链表头节点while (p != NULL) {Node *q = p->next;Node *prev = NULL;Node *cur = *head;while (cur != NULL && cur->data < p->data) {prev = cur;cur = cur->next;}if (prev == NULL) { // 插入到头节点之前p->next = *head;*head = p;} else { // 插入到prev和cur之间prev->next = p;p->next = cur;}p = q;}
}
此代码首先对链表的头节点进行判断,若链表为空或只有一个节点则不需要排序。然后指针p指向头节点的后继节点,将头节点的后继节点设为空,新的有序链表头节点为原链表的头节点。接下来,对p的每个节点进行插入排序操作,找到p应该插入的位置并插入。最后返回排好序的链表头节点。
3、折半插入排序
3.1 算法思想
折半插入排序算法是插入排序算法的一种变种。它的基本思想是将待排序的序列分成两部分,前半部分为已排序好的部分,后半部分为未排序的部分。排序过程中,每次从未排序的部分中选出一个元素,通过折半查找的方式,找到它应该插入到已排序的部分中的哪个位置,然后再将的元素插入到已排序的部分中。
具体实现步骤如下:
1. 将待排序序列的第一个元素作为已排序的部分,剩下的元素作为未排序的部分。
2. 从未排序的部分中选出一个元素,通过二分查找找到它应该插入到已排序的部分中的位置。
3. 将该元素插入到已排序的部分中,同时将已排序的部分的长度增加1,未排序的部分的长度减少1。
4. 重复步骤2和步骤3,直到未排序的部分为空。
折半插入排序算法相比于普通的插入排序算法,虽然查找的时间复杂度由O(n)降低为O(log n),但是这并不影响算法的总体时间复杂度,依然是O(n^2)。不过,在某些特定的场景下,折半插入排序算法的效率可能会比普通的插入排序算法更高。
3.2 代码实现
折半插入排序是插入排序的一种优化算法,它利用二分查找的思想来确定插入位置,从而减少比较和移动的次数,提高排序效率。
下面是C语言实现折半插入排序的示例代码:
void binary_insertion_sort(int arr[], int len) {int i, j, left, right, mid, tmp;for (i = 1; i < len; i++) {tmp = arr[i];left = 0;right = i - 1;// 找到插入位置while (left <= right) {mid = (left + right) / 2;if (tmp < arr[mid]) {right = mid - 1;} else {left = mid + 1;}}// 移动元素for (j = i - 1; j >= left; j--) {arr[j + 1] = arr[j];}// 插入元素arr[left] = tmp;}
}
该算法的时间复杂度为O(nlogn),空间复杂度为O(1)。
4、希尔排序
4.1 算法思想
希尔排序算法是插入排序的一种改进算法,也称为缩小增量排序。希尔排序的基本思想是将待排序序列分割成若干个子序列,对每个子序列进行插入排序,然后不断减小步长,直到步长为1,完成排序。
具体实现时,先确定一个增量,在每个增量下将序列分成若干个小组,对每个小组进行插入排序。然后逐渐减小增量,重复上述操作,直到增量减小为1,再进行一次插入排序。不同的增量序列会影响希尔排序的效率,一般采用Hibbard增量序列或Sedgewick增量序列来提高排序效率。
希尔排序算法时间复杂度为O(nlogn)到O(n^2)之间,取决于增量序列的选择。在一般情况下,希尔排序具有较好的排序效率和稳定性,特别适用于数据量较大、无序性较强的序列。
4..2 代码实现
下面是C语言实现希尔排序的代码:
void shell_sort(int arr[], int len)
{int gap, i, j, temp;for (gap = len / 2; gap > 0; gap /= 2) { // gap为步长,每次减半直到为1for (i = gap; i < len; i++) {temp = arr[i];for (j = i - gap; j >= 0 && arr[j] > temp; j -= gap) {arr[j + gap] = arr[j]; // 向后移动gap位}arr[j + gap] = temp; // 插入到正确位置}}
}
该代码首先将整个待排序序列分成若干个子序列,按照步长进行插入排序。然后逐渐缩小步长,直至为1,最后进行一次普通的插入排序,完成整个排序过程。
相关文章:

【数据结构】插入排序:直接插入排序、折半插入排序、希尔排序的学习知识总结
目录 1、排序的基本概念 2、直接插入排序 2.1 算法思想 2.2 代码实现 3、折半插入排序 3.1 算法思想 3.2 代码实现 4、希尔排序 4.1 算法思想 4..2 代码实现 1、排序的基本概念 排序是将一组数据按照预定的顺序排列的过程,排序的基本概念包括以下内容…...
Magic Battery for Mac:让你的设备电量管理变得轻松简单
Mac电脑用户们,你们是否曾经为了给设备充电而感到烦恼?是否希望能够方便地查看连接设备的电量情况?现在,有了Magic Battery for macOS,这些问题都将成为过去! Magic Battery是一个实用的应用程序ÿ…...
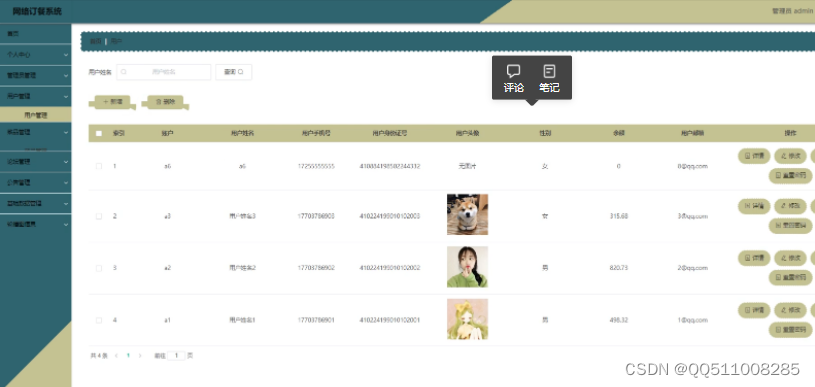
nodejs+vue大学食堂订餐系统elementui
可以查看会员信息,录入新的会员信息,对会员的信息进行管理。 网站管理模块对整个网站中的信息进行管理,可以查看会员留在留言栏中的信息,设置网站中的参数等。用户管理模块主要实现用户添加、用户修改、用户删除等功能。 近年来&…...

nat综合实验
路漫漫其修远兮,吾将上下而求索。 实验目的如图 实验思路:配置内网,再配置外网,再做nat clien1配置 clien2配置 pc3配置 lsw1配置 sysname lsw1 # vlan batch 10 20 30 # interface MEth0/0/1 # interface Eth-Trunk1port link-type trunkp…...

【iOS逆向与安全】好用的一套 TCP 类
初始化 //页面 %hook xxxxxxxViewController//- (void)viewWillAppear:(BOOL)animated{ //NSLog("View Will Appear,再次进入刷新"); - (void)viewDidLoad{//启动tcp[[Xddtcp sharedTcpManager] connectServer] ;} 发送数据 //发送数据 [[Xddtcp shared…...

Ubuntu Kafka开机自启动服务
1、创建service文件 在/lib/systemd/system目录下创建kafka.service文件 [Unit] DescriptionApache Kafka Server Documentationhttp://kafka.apache.org/documentation.html Requireszookeeper.service[Service] Typesimple Environment"JAVA_HOME/usr/local/programs/j…...
)
c#实现单例模式的两种方法(饿汉式、懒汉式)
在C#中,可以使用以下几种方式来实现单例模式: 饿汉式单例模式(Eager Singleton): 在类加载时就创建实例。私有化构造函数,防止外部实例化。提供一个静态的只读属性来获取实例。代码示例: // 在C…...

Git与Repo:开源开发的得力工具组合
Git与Repo:开源开发的得力工具组合 1. 引言 开源开发在当今的软件行业中扮演着至关重要的角色。它不仅推动了技术的创新和进步,也促进了开发者之间的合作与共享。随着越来越多的开源项目的涌现,有效的代码管理和版本控制成为了必不可少的工…...
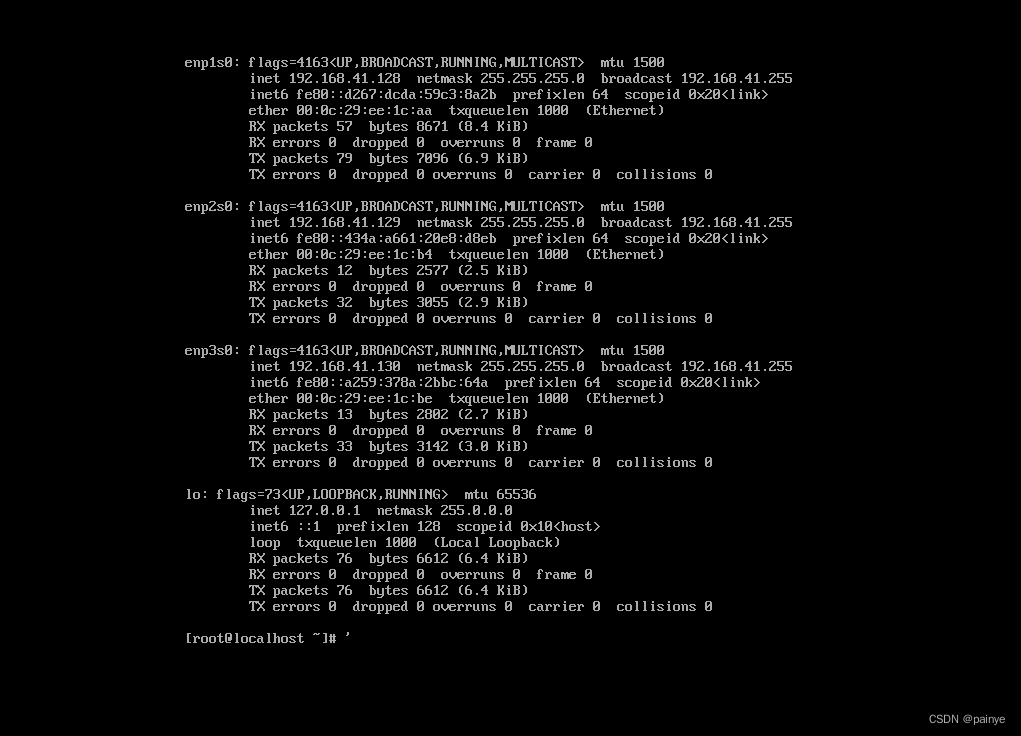
centos7 添加网卡设置动态ip,修改网卡为任意名称
centos7 添加网卡并设置动态ip,重命名为任意名称 本文记录如何在centos环境上增加两个网卡,并设置为动态获取ip,以及修改网卡名称为任意名称 1、centos7添加两个网卡动态获取ip 1.1 vmvare上添加网络适配器 1、关闭虚拟机 2、 添加网络适…...
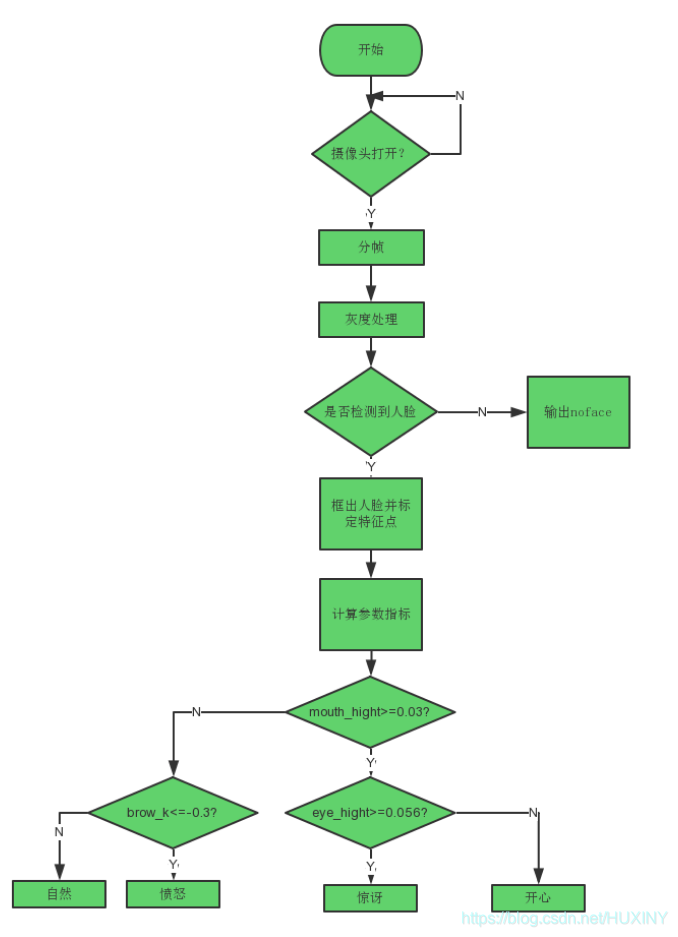
计算机竞赛 深度学习人脸表情识别算法 - opencv python 机器视觉
文章目录 0 前言1 技术介绍1.1 技术概括1.2 目前表情识别实现技术 2 实现效果3 深度学习表情识别实现过程3.1 网络架构3.2 数据3.3 实现流程3.4 部分实现代码 4 最后 0 前言 🔥 优质竞赛项目系列,今天要分享的是 🚩 深度学习人脸表情识别系…...
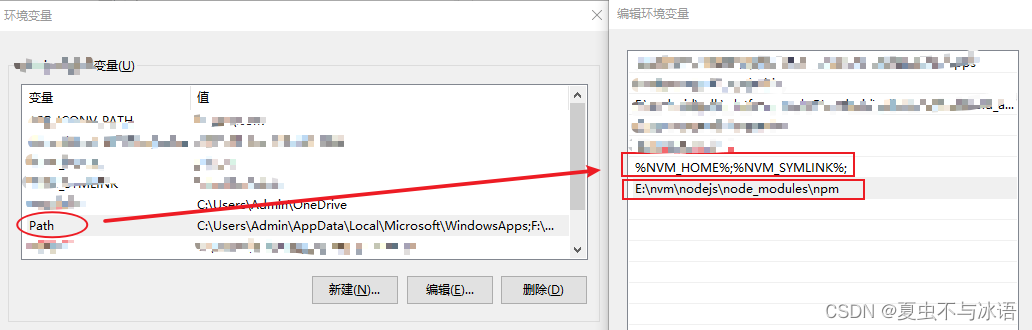
nvm安装后node或npm不是内部或外部命令
nvm安装后出现node或npm不是内部或外部命令 进行以下步骤解决 找到nvm安装所在位置,新建一个空的nodejs文件夹 打开 windowr —> sysdm.cpl —> 高级 —>环境变量 将下图中两个位置的地址改成刚刚新建的nodejs空文件夹所在的位置 nvm安装后都是会自动添加…...
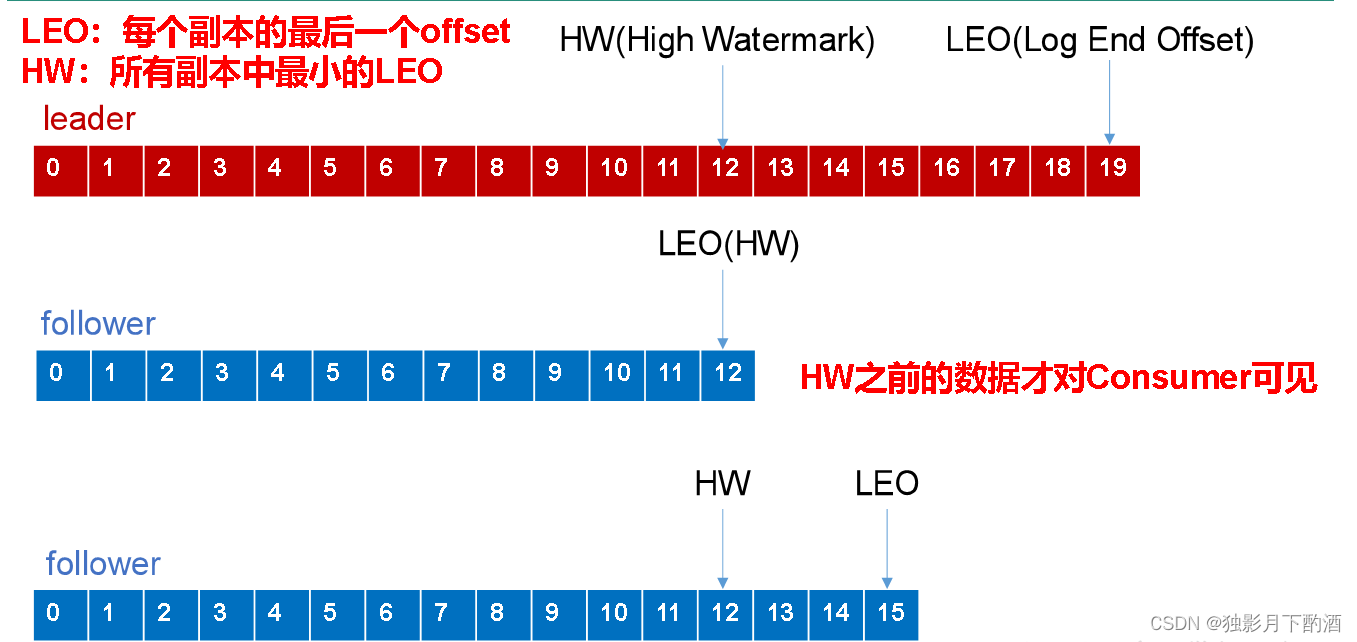
Kafka数据可靠性保证
1.生产者发送数据到Topic partition的可靠性保证 为保证producer发送的数据,能可靠的发送到指定的topic,topic的每个partition收到producer发送的数据后,都需要向producer发送ack(acknowledgement确认收到),…...
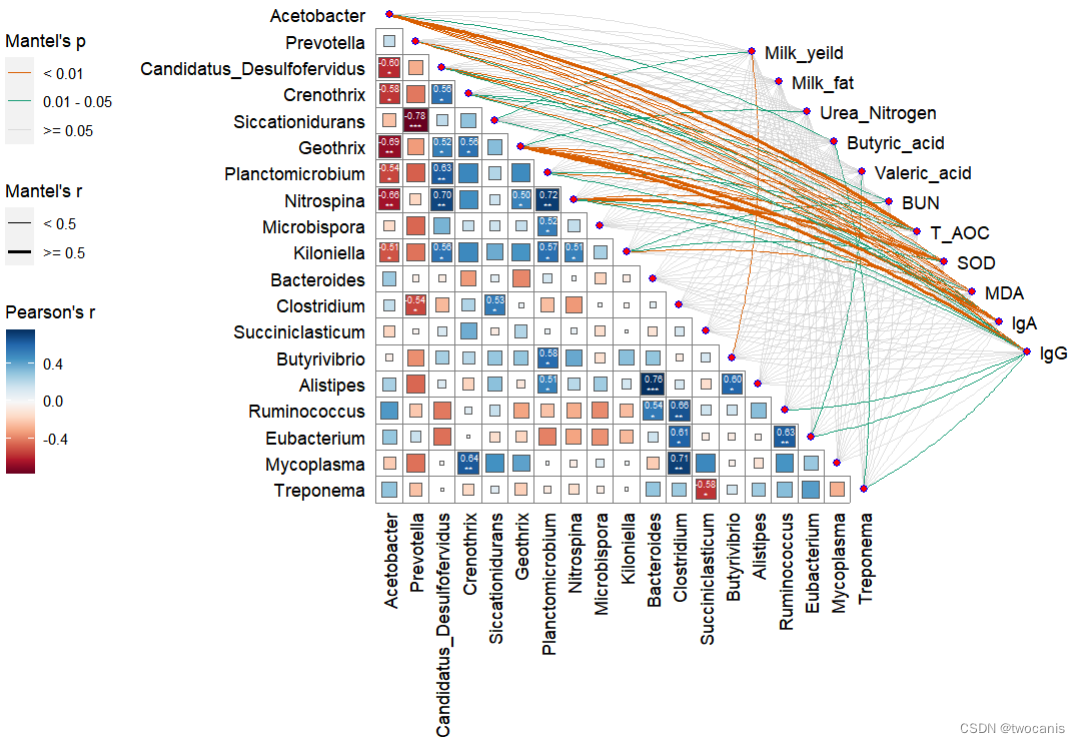
基于R的linkET包qcorrplot可视化Mantel test相关性网络热图分析correlation heatmap
写在前面 需求是对瘤胃宏基因组结果鉴定到的差异菌株与表观指标、瘤胃代谢组、血清代谢组、牛奶代谢组中有差异的部分进行关联分析,效果图如下: 数据准备 逗号分隔的csv格式文件,两个表格,一个是每个样本对应的表观指标数据&…...

IOTDB的TsFile底层设计
目录 概述 数据模型 数据结构 元数据注册 读取和写入 设计思想 主要过程...
)
MATLAB算法实战应用案例精讲-【人工智能】边缘计算(补充篇)
目录 前言 算法原理 传统边缘检测算子 构建通用的边缘检测算子 图...
Linux学习-HIS系统部署(1)
Git安装 #安装中文支持(选做) [rootProgramer ~]# echo $LANG #查看当前系统语言及编码 en_US.UTF-8 [rootProgramer ~]# yum -y install langpacks-zh_CN.noarch #安装中文支持 [rootProgramer ~]# vim /etc/locale.co…...
)
Cairo介绍及源码构建安装(3)
接前一篇文章:Cairo介绍及源码构建安装(2) 四、Cairo构建与安装 2. 配置 BLFS中给出的命令为: ./configure --prefix/usr \--disable-static \--enable-tee 这里将“--prefix”选项由“/usr”调整为“/usr/local”&#x…...

Mac电脑信息大纲记录软件 OmniOutliner 5 Pro for Mac中文
OmniOutliner 5 Pro是一款专业级的Mac大纲制作工具,它可以帮助用户更好地组织和管理信息,以及制作精美的大纲。以下是OmniOutliner 5 Pro的主要功能和特点: 强大的大纲组织和管理功能。OmniOutliner 5 Pro为用户提供了多层次的大纲结构&…...
)
linux设置应用开机自启(通用:mysql、jar、nginx、solr...)
1. 业务场景 用于单机生产环境,防止服务器断电或者强制重启导致的服务下线。 2. 实现方案 对于无状态服务,可容器部署设置 restart: always,systemctl eable docker对于有状态服务,可编写自启脚本,如下 ① 编写执行…...

Offset Explorer(Kafka消息可视化工具)报invalid hex digit ‘{‘错误解决方法
解决办法: 根据代码的实际情况,设置成对应的值。设置完成后点update、refresh更新。...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...
