C语言数组和指针笔试题(四)(一定要看)
目录
- 二维数组
- 例题一
- 例题二
- 例题三
- 例题四
- 例题五
- 例题六
- 例题七
- 例题八
- 例题九
- 例题十
- 例题十一
- 结果
感谢各位大佬对我的支持,如果我的文章对你有用,欢迎点击以下链接
🐒🐒🐒个人主页
🥸🥸🥸C语言
🐿️🐿️🐿️C语言例题
🐣🐓🏀python
二维数组
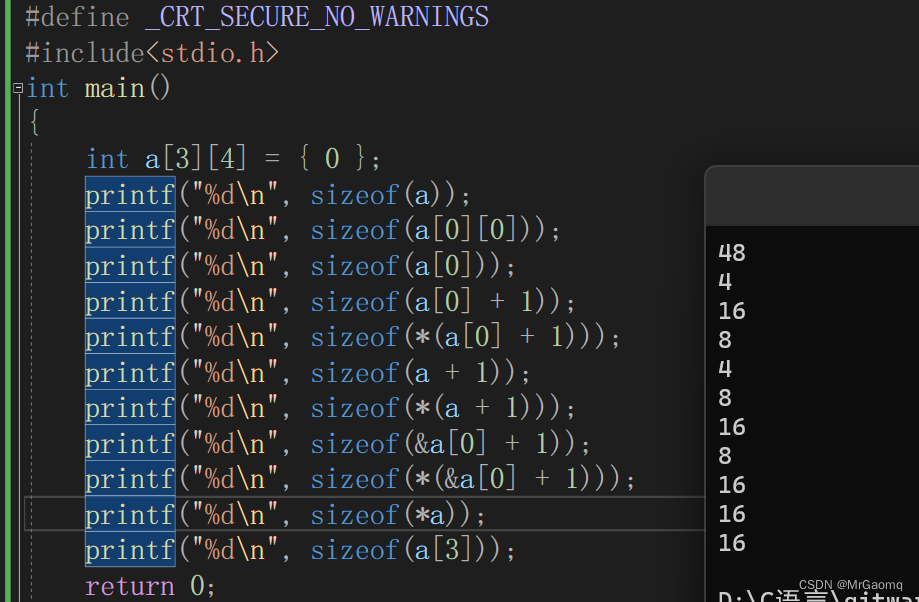
1:int a[3][4] = {0};
2:printf("%d\n",sizeof(a));
3:printf("%d\n",sizeof(a[0][0]));
4:printf("%d\n",sizeof(a[0]));
5:printf("%d\n",sizeof(a[0]+1));
6:printf("%d\n",sizeof(*(a[0]+1)));
7:printf("%d\n",sizeof(a+1));
8:printf("%d\n",sizeof(*(a+1)));
9:printf("%d\n",sizeof(&a[0]+1));
10:printf("%d\n",sizeof(*(&a[0]+1)));
11:printf("%d\n",sizeof(*a));
12:printf("%d\n",sizeof(a[3]));
在做之前我们再来复习一下数组名的意义
- sizeof(数组名),这里的数组名表示整个数组,计算的是整个数组的大小。
- &数组名,这里的数组名表示整个数组,取出的是整个数组的地址。
- 除此之外所有的数组名都表示首元素的地址
例题一
1:int a[3][4] = {0};
2:printf("%d\n",sizeof(a));
这里的a是整个数组的地址,所以sizeof会计算整个数组的内存大小,因此结果就是(3*4)(数组的元素)*4(整形类型的大小)=48
例题二
1:int a[3][4] = {0};
2:printf("%d\n",sizeof(a[0][0]));
这里的a[0][0]是指的数组首元素,因为是特别指定的一个元素,所以只需要计算整个元素的内存大小即可,因此a[0][0]是一个整形类型的元素,结果就是4
例题三
1:int a[3][4] = {0};
2:printf("%d\n",sizeof(a[0]));
a[0]是表示的第一行的数组元素,为了方便理解,我们暂时将数组中的元素改变一下,调试结果如图
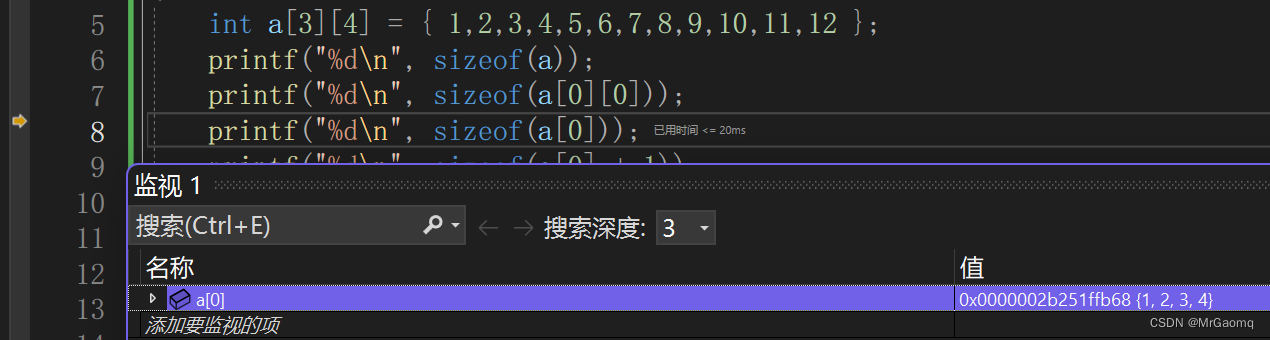
显然这里的a[0]是指的数组第一行,而不是第一列,第一行元素有4个,因此结果应该是4(第一行元素)*4(整形类型的大小)=16
另外这里顺便补充一下
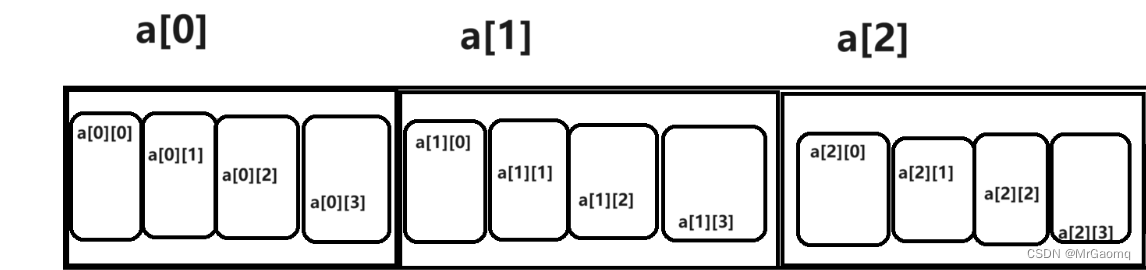
我们可以将二维数组表示成这样
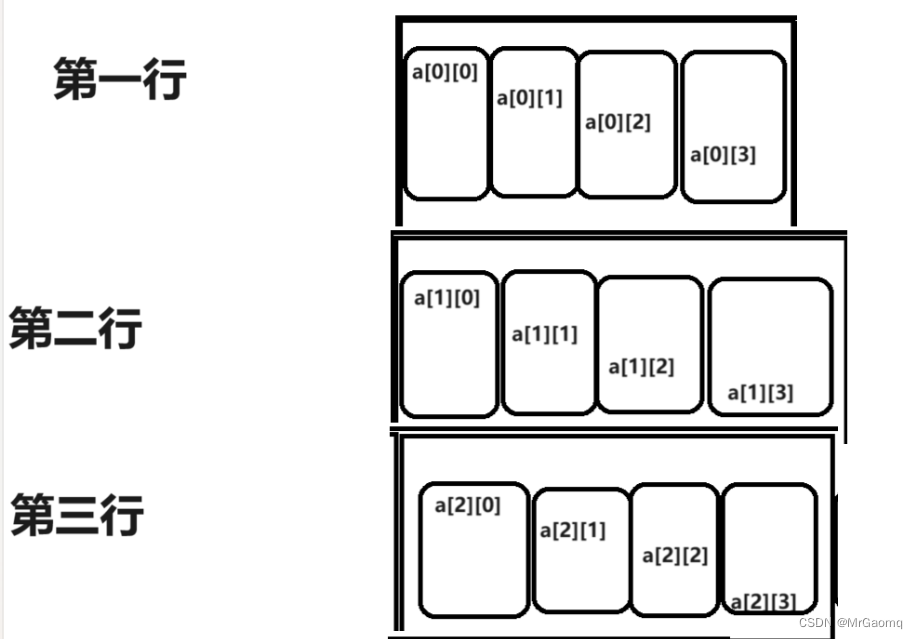
但实际上二维数组的存储方式和上图是有一些区别的
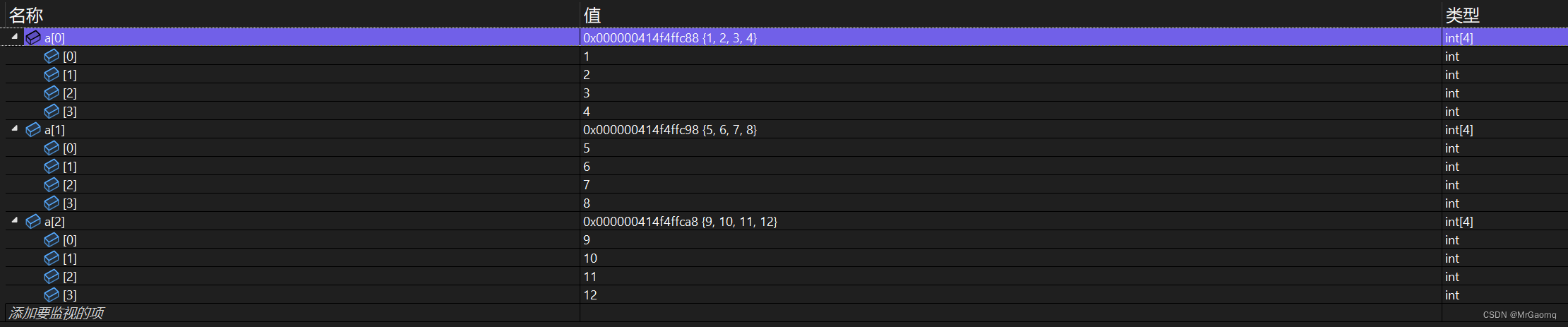
这是每一行的地址,我们再来看一下每个元素的地址
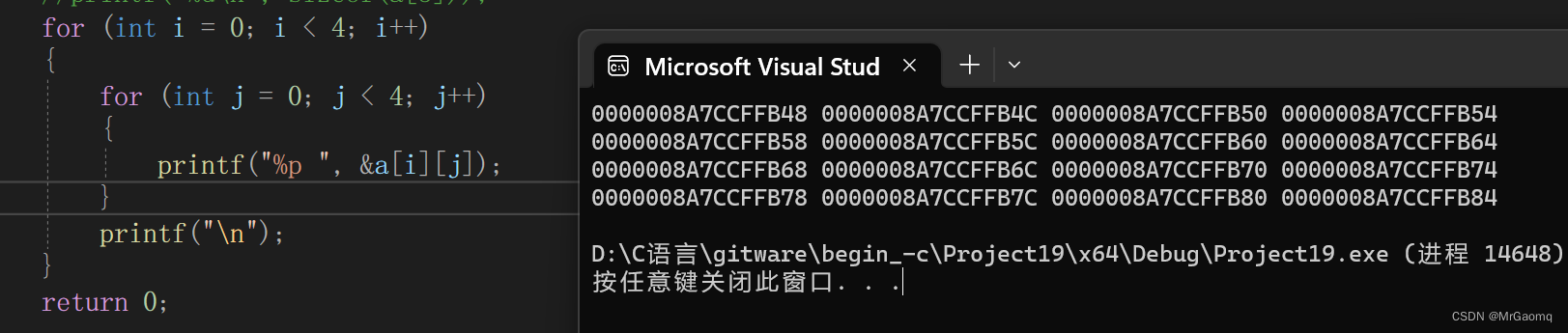
这是每一行的每一个元素,地址的表示方式是16进制,因此我们可以看出每一个元素的地址相差为4个字节,第二行的首元素和第一行末尾的元素地址相差也是4个字节,因此我们可以推断出,二维数组的存储是下一行首元素地址接在上一行末尾元素的地址上,存储方式如图
例题四
1:int a[3][4] = {0};
2:printf("%d\n",sizeof(a[0]+1));
这里可能会有人非常纠结,a[0]+1是直接跳过第一行,还是直接跳过第一行的第一个元素,我们来看看调试的结果
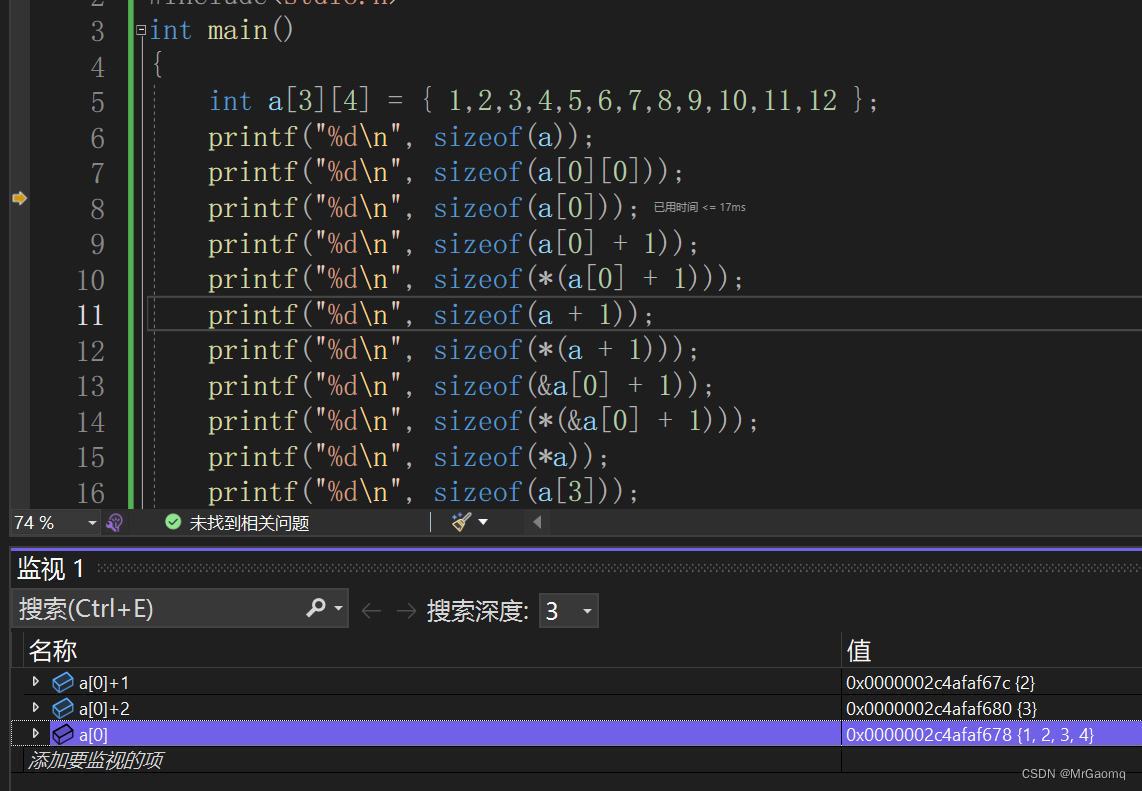
a[0]+1是跳过第一行第一个元素,但是我们可以看到单独的a[0]却表示的整个第一行元素,这是为什么呢?
其实二维数组我们可以这样写(下面的元素是为了方便理解所以改的)
a[3][4]={{1,2,3,4},{5,6,7,8},{9,10,11,12}},这有点类似于数学中的换元
这里我们将二维数组看出一维数组,将二维数组的每一行元素整体看成一个元素,{1,2,3,4}就相当于换元中的t ,而要换的元素就是1,2,3,4
因此a[0]就是换元之后的第一个元素,a[0]={1,2,3,4},而a[0]+1就是在换元前的四个元素中寻找第二个元素
例题五
1:int a[3][4] = {0};
2:printf("%d\n",sizeof(*(a[0]+1)));
上一题已经讲过了a[0]+1是第一行中的第二个元素,对这个元素解引用就是一个整形类型,所以结果就是4
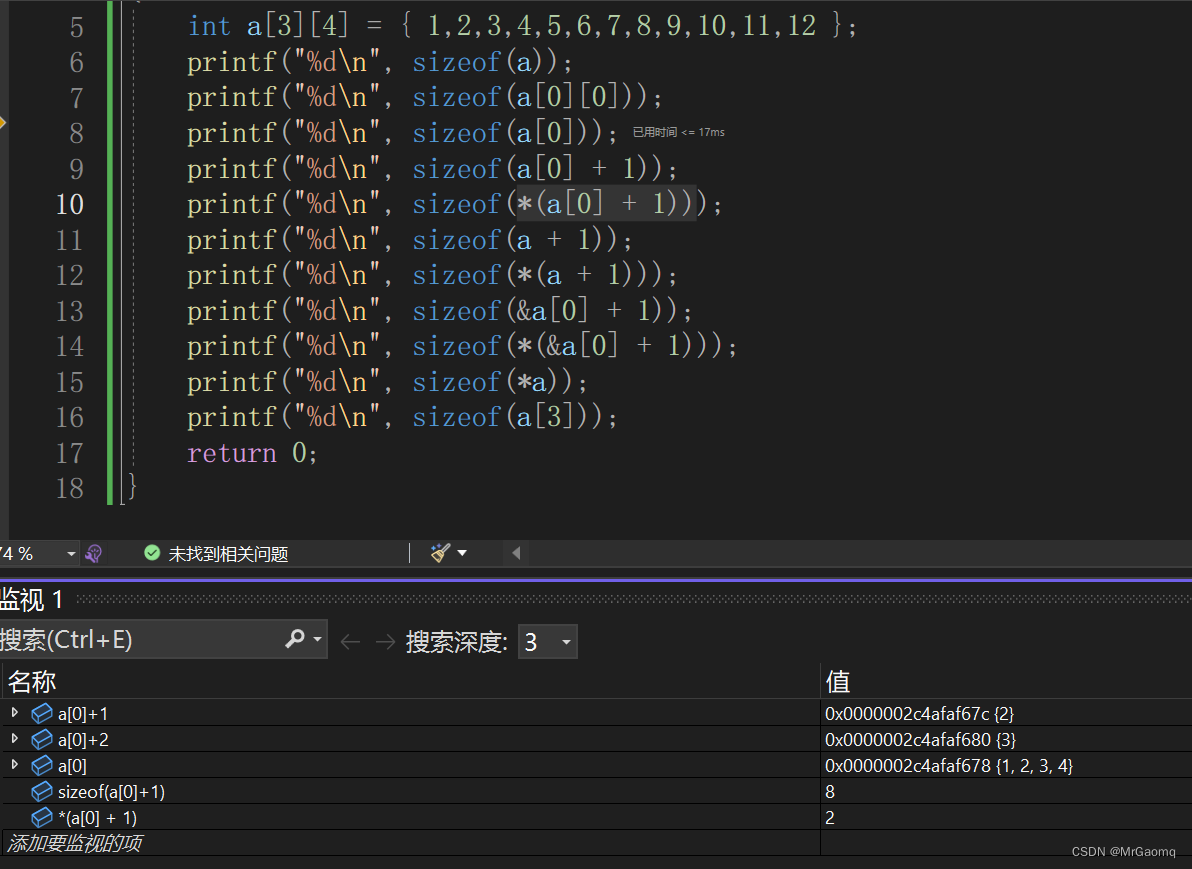
这里我们可以看出a[0]+1其实是一个地址,所以我们可以推断二维数组存的是一位数组的地址,也就是说a[3]={&b[0],&b[1],&b[2],&b[3]},这里的数组b就是每一行的元素
例题六
1:int a[3][4] = {0};
2:printf("%d\n",sizeof(a+1));
这里的a不是单独放在括号里的,所以a表示第一行的地址,a+1就是跳过第一行,所以a+1=a[1]是第二行的地址,既然是地址结果就为4或者8
例题七
1:int a[3][4] = {0};
2:printf("%d\n",sizeof(*(a+1));
这里的a+1上一题已经说过了,是第二行的地址,对第二行地址解引用,就是第二行的四个元素,所以结果就是4*4=16
例题八
1:int a[3][4] = {0};
2:printf("%d\n",sizeof(&a[0]+1));
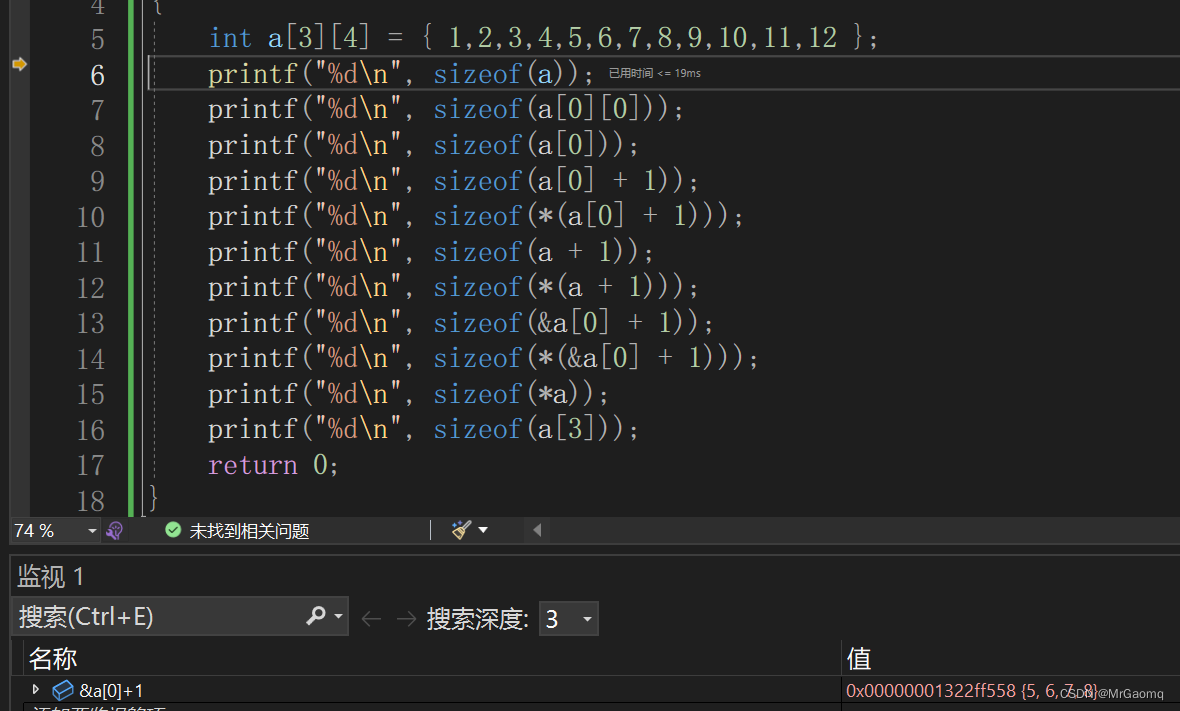
&a[0]是第一韩的地址,&a[0]+1为第二行的地址所以结果为4或者8,也可以用前面换元的思想去理解,
a[3][4]={{0,0,0,0},{0,0,0,0},{0,0,0,0},{0,0,0,0}},这里的a[0]是第一个{0,0,0,0},而a[0]+1=a[1]
a[1]=第二个{0,0,0,0},但注意这里的是&a[0]+1,&a[0]+1=&a[1]
例题九
1:int a[3][4] = {0};
2:printf("%d\n",sizeof(*(&a[0]+1)));
对第二行的地址进行解引用就是第二行的四个元素,所以结果就是4*4=16
例题十
1:int a[3][4] = {0};
2:printf("%d\n",sizeof(*a));
这里的a因为不是单独放在括号里的(有个号),所以这里的a就表示第一行元素,结果就是44=16
例题十一
1:int a[3][4] = {0};
2:printf("%d\n",sizeof(a[3]));
a[3]和之前的a[0] a[1]是一样的,表示的是第四行元素,结果就是4*4=16
结果
相关文章:

C语言数组和指针笔试题(四)(一定要看)
目录 二维数组例题一例题二例题三例题四例题五例题六例题七例题八例题九例题十例题十一 结果 感谢各位大佬对我的支持,如果我的文章对你有用,欢迎点击以下链接 🐒🐒🐒个人主页 🥸🥸🥸C语言 🐿️…...
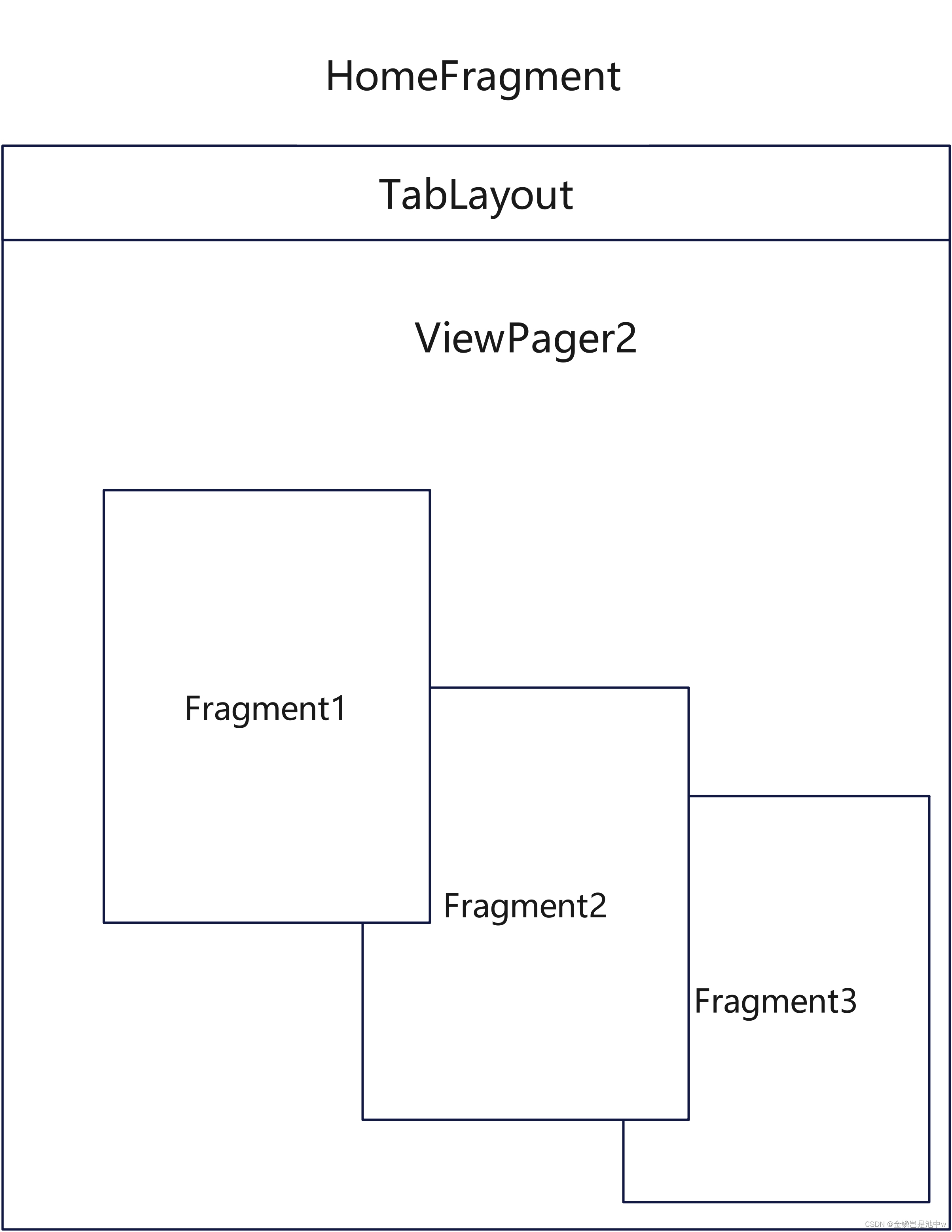
FragmentManager is already executing transactions
本文解决问题: java.lang.IllegalStateException: FragmentManager is already executing transactions 问题背景描述: 在Fragment中 用tablayoutviewpagerfragment,即Fragment嵌套Fragment场景、或者ViewPager2嵌套ViewPager2时。 执行生命…...

Matlab中clear,close all,clc功能详细说明
背景: 我们在写matlab程序时,首行总是先敲入:clear; close all; clc;,但你真的知道这三句话的具体作用嘛,下面进行详细说明和演示。 一、clear的功能 clear的功能:清理工作区变量,不清理前是…...

Typora安装无需破解免费使用
Typora简介: 在介绍Typora软件之前,需要先介绍一下MARKDOWN。 MARKDOWN是一种轻量型标记语言,它具有“极简主义”、高效、清晰、易读、易写、易更改纯文本的特点。 Typora 是一款支持实时预览的 Markdown 文本编辑器。它有 OS X、Windows、…...
--errDump - 错误上报)
LuatOS-SOC接口文档(air780E)--errDump - 错误上报
示例 -- 基本用法, 10分钟上报一次,如果有的话 if errDump thenerrDump.config(true, 600) end-- 附开源服务器端: https://gitee.com/openLuat/luatos-devlogerrDump.dump(zbuff, type, isDelete) 手动读取异常日志,主要用于用户将日志发送给自己的服务器而不是I…...

低代码平台如何助力国内企业数字化转型?
数字化是什么 数字化(Digitalization)是将许多复杂多变的信息转变为可以度量的数字、数据,再以这些数字、数据建立起适当的数字化模型,把它们转变为一系列二进制代码,引入计算机内部,进行统一处理…...
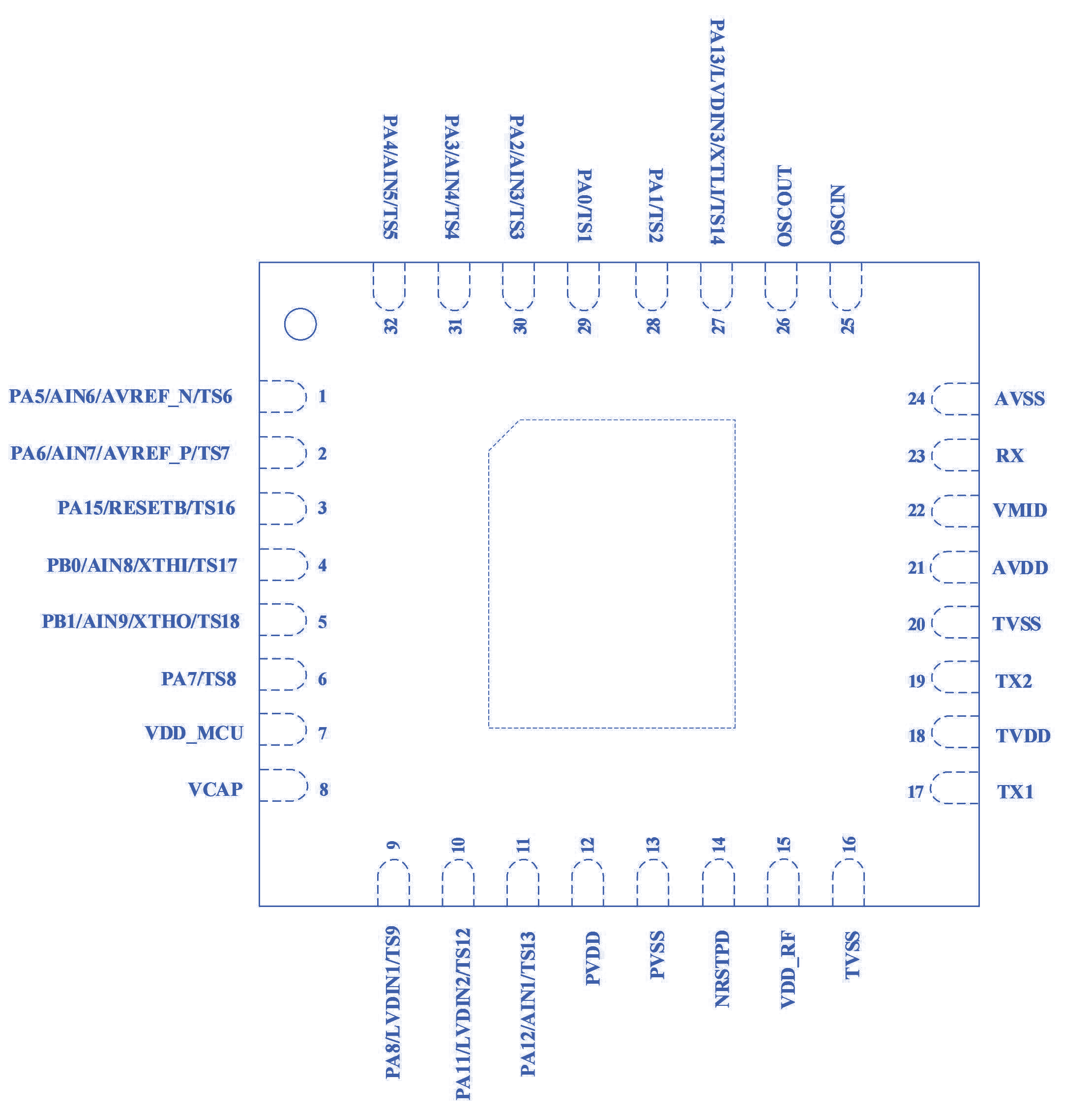
SI3262—高度集成的低功耗SOC芯片
Si3262是一款高度集成的低功耗SOC芯片,其集成了基于RISC-V核的低功耗MCU和工作在13.56MHz的非接触式读写器模块。 MCU模块具有低功耗、Low Pin Count、宽电压工作范围,集成了13/14/15/16位精度的ADC、LVD、UART、SPI、I2C、TIMER、WUP、IWDG、RTC、TSC等…...

除静电离子风机在无尘车间的应用
除静电离子风机在无尘车间中的应用非常广泛,主要是用来控制车间内的静电荷,防止静电对车间内的电子元器件、电路板等敏感部件产生损害。 具体来说,除静电离子风机通常采用电离器产生大量负离子,将车间内的静电荷中和成无害的水蒸气…...

Linux上的Pip和Python升级指南
在Linux系统上,保持Pip和Python版本的最新状态对于顺利进行Python开发至关重要。通过升级Pip和Python,你可以享受到最新的功能、修复的bug以及提升的开发效率。本文将为你提供在Linux上升级Pip和Python的详细指南,助你打造更强大的开发环境。…...

4G工业路由器高效数据传输助力光伏发电站管理
光伏发电站是能源产业中一种利用太阳能技术将光转化为电能的常见设施。随着物联网技术与环保能源的不断进步和应用的普及,光伏发电站的管理也变得更加便捷高效。 光伏发电站结合4G工业路由器实现远程监控管理,并用于采集发电站中的传感器数据和监控信息…...

【音视频笔记】Mediacodec+Muxer生成mp4,浏览器无法播放问题处理
文章目录 背景解决过程曲线修复方案 解决问题根源 背景 最近在测试视频录制功能时发现,AudioRecord MediaCodec MediaMuxer生成的MP4,PC浏览器无法播放 ,但是Android、Windows、Mac的播放器应用都能正常播放。虽然不禁想吐槽浏览器视频组件…...
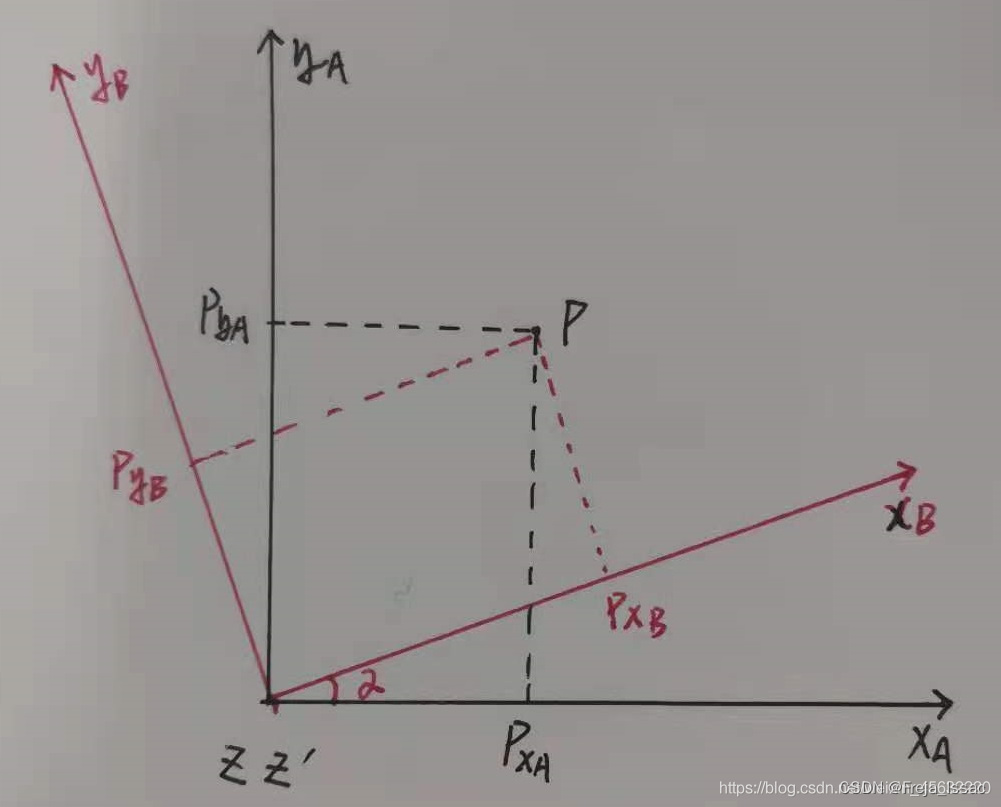
debug过程中,矩阵左乘右乘相关概念梳理
1. 变换点或者变换向量 1.1左乘 矩阵左乘通常是指对”目标点“进行左乘,即: A ′ R ∗ A AR*A A′R∗A 其中,A为原始3维点,表示一个3*1的列向量,R为33的旋转矩阵,A‘为变换后的点 B ′ T ∗ B BT*B B′T∗B 其中…...
Ubuntu 安装Kafka
在本指南中,我们将逐步演示如何在 Ubuntu 22.04 上安装 Apache Kafka。 在大数据中,数以百万计的数据源生成了大量的数据记录流,这些数据源包括社交媒体平台、企业系统、移动应用程序和物联网设备等。如此庞大的数据带来的主要挑战有两个方面…...

洗地机性价比高的是哪款?高性价比洗地机排名
洗地机已成为当下备受欢迎的智能家电之一,但在挑选合适的洗地机时,面对各种新词汇和功能选择,可能会让人感到困惑。因此,为了帮助大家在购买洗地机时不踩坑,我们基于市面上主流品牌的综合分析对比,总结出来…...

安装konga
创建konga数据库 docker run --rm pantsel/konga:latest -c prepare -a postgres -u postgresql://kong:kong{IP}:5432/konga这里要注意docker部署时IP不能直接访问localhost 安装konga docker run -p 1337:1337 \--network kong-net \--name konga \-e "NODE_ENVprodu…...

算法基础之高精度总结
目录 高精度算法分类 高精度加减乘除的异同点 加和乘 相同点 减和除 相同点 不同点 处理前导0的方式 高精度算法分类 分类:加、减、乘、除 其中加减乘都适用于两个数都是高精度,除法因为除数是高精度的话不好用整除的方法,所以除法时…...
oracle TNS Listener 远程投毒漏洞修复
有个客户在等保测评过程,测评公司扫出一个关于oracle的漏洞如下: 客户是RAC环境11.2.0.4,在生产修复漏洞前我做了如下测试验证: 测试环境准备: RAC一套11.2.0.4 实例名dbserver [oraclehisdb1 ~]$ cat /etc/hosts …...
)
第二章:最新版零基础学习 PYTHON 教程(第一节 - Python 输入/输出–在 Python 中获取输入)
开发人员经常需要与用户交互,以获取数据或提供某种结果。如今,大多数程序都使用对话框来要求用户提供某种类型的输入。而Python为我们提供了两个内置函数来读取键盘输入。 目录 输入(提示) raw_input(提示) 输入函数在 Python 中的工作原理:...
react create-react-app v5 从零搭建项目
前言: 好久没用 create-react-app做项目了,这次为了个h5项目,就几个页面,决定自己搭建一个(ps:mmp 好久没用,搭建的时候遇到一堆问题)。 我之前都是使用 umi 。后台管理系统的项目 使用 antd-…...
2023软件测试八股文,涵盖所有面试题
Part1 1、你的测试职业发展是什么? 测试经验越多,测试能力越高。所以我的职业发展是需要时间积累的,一步步向着高级测试工程师奔去。而且我也有初步的职业规划,前3年积累测试经验,按如何做好测试工程师的要点去要求自…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...
