4.迭代最近点ICP及非线性优化求解
使用非线性优化方法求解ICP
文章目录
- 使用非线性优化方法求解ICP
- 前情提要
- ICP问题回顾
- 对矩阵变量求导数
- ICP问题的非线性解法
- 代码示例
欢迎访问个人网络日志🌹🌹知行空间🌹🌹
前情提要
在迭代最近点算法ICP及SVD求解中介绍了ICP问题及使用SVD分解求解ICP的方法。除了SVD,还可以使用非线性优化的方法来求解ICP。
ICP问题回顾
还记得,ICP优化的目标函数为:
min R , t 1 2 ∑ i n ∣ ∣ p i − ( R q i + t ) ∣ ∣ 2 2 \min\limits_{R,t}\frac{1}{2}\sum\limits_{i}^n||p_i-(Rq_i+t)||_2^2 R,tmin21i∑n∣∣pi−(Rqi+t)∣∣22
我们知道旋转和平移可以写成齐次变换的形式,
T = [ R t 0 0 ] T=\begin{bmatrix} R & t\\ 0 &0 \end{bmatrix} T=[R0t0]
ICP优化的目标函数可以写成:
min T 1 2 ∑ i n ∣ ∣ p i − T q i ∣ ∣ 2 2 \min\limits_{T}\frac{1}{2}\sum\limits_{i}^n||p_i-Tq_i||_2^2 Tmin21i∑n∣∣pi−Tqi∣∣22
这里要优化的变量是 T T T,而 T T T是矩阵?如何对矩阵求导数呢?需要使用李群与李代数的概念。
对矩阵变量求导数
根据《视觉SLAM十四讲》第4讲的介绍, T T T属于特殊欧式群 S E ( 3 ) SE(3) SE(3), S E ( 3 ) SE(3) SE(3)具有连续性质,是李群。
李群局部正切空间上的表示是李代数,李代数相对于李群,类似于导数对函数的意义。
S E ( 3 ) SE(3) SE(3)对应的李代数 s e ( 3 ) \mathcal{se(3)} se(3)为:
s e ( 3 ) = { ξ = [ ρ ϕ ] ∈ R 6 , ρ ∈ R 3 , ϕ ∈ s o ( 3 ) , ξ ∧ = [ ϕ ∧ ρ 0 T 0 ] ∈ R 4 × 4 } \mathcal{se}(3)=\left \{ \xi = \begin{bmatrix} \rho \\ \phi \end{bmatrix} \in \mathbb{R}^6, \rho \in \mathbb{R}^3 ,\phi \in \mathcal{so}(3), \xi^{\wedge } = \begin{bmatrix} \phi ^{\wedge } & \rho \\ 0^T & 0 \end{bmatrix} \in \mathbb{R}^{4\times 4} \right \} se(3)={ξ=[ρϕ]∈R6,ρ∈R3,ϕ∈so(3),ξ∧=[ϕ∧0Tρ0]∈R4×4}
其中, ξ \xi ξ是 s e ( 3 ) \mathcal{se}(3) se(3)的元素,是包含平移 ρ \rho ρ和旋转 ϕ \phi ϕ的六维向量。 ϕ \phi ϕ其实是 s o ( 3 ) \mathcal{so}(3) so(3)的元素。
∧ {\wedge } ∧符号这里表示将六维向量转换成四维矩阵。
在 t = 0 t=0 t=0附近,齐次变换矩阵可以由 T = e x p ( ξ 0 t ) T=exp(\xi_0t) T=exp(ξ0t)计算出来,由此可以看到,齐次变换矩阵与一个反对称矩阵 ξ 0 ∧ t \xi_0 ^{\wedge }t ξ0∧t建立了联系,在一时刻对于给定的 T T T,可以求得一个 ξ \xi ξ,其描述了 T T T在局部的导数关系。
矩阵的指数运算显然没有定义,如何计算呢?这里可以用泰勒公式,
e x p ( A ) = ∑ n = 0 ∞ 1 n ! A n exp(A)=\sum\limits _{n=0}^{\infty }\frac{1}{n!}A^n exp(A)=n=0∑∞n!1An
将 ξ \xi ξ写成旋转加平移的形式 [ ρ , ϕ ] T [\rho, \phi]^T [ρ,ϕ]T,再将 ϕ \phi ϕ写成模长和方向的形式 ϕ = θ a \phi=\theta a ϕ=θa,代入上面的公式可得:
e x p ( ξ ∧ ) = [ ∑ n = 0 ∞ 1 n ! ( ϕ ∧ ) n ∑ n = 0 ∞ 1 ( n + 1 ) ! ( ϕ ∧ ) n ρ 0 1 ] ≜ [ R J ρ 0 T 1 ] = T exp(\xi^{\wedge})=\begin{bmatrix} \sum\limits_{n=0}^{\infty}\frac{1}{n!}(\phi ^\wedge )^n & \sum\limits_{n=0}^{\infty}\frac{1}{(n+1)!}(\phi ^\wedge )^n\rho \\ 0 & 1 \end{bmatrix}\triangleq \begin{bmatrix} R & J\rho \\ 0^T &1 \end{bmatrix}=T exp(ξ∧)= n=0∑∞n!1(ϕ∧)n0n=0∑∞(n+1)!1(ϕ∧)nρ1 ≜[R0TJρ1]=T
当 ϕ = θ a \phi=\theta a ϕ=θa时,推导可得
J = s i n θ θ I + ( 1 − s i n θ θ ) a a T + 1 − c o s θ θ a ∧ J=\frac{sin\theta}{\theta}I+(1-\frac{sin\theta}{\theta})aa^T+\frac{1-cos\theta}{\theta}a^\wedge J=θsinθI+(1−θsinθ)aaT+θ1−cosθa∧
当在李群中完成两个矩阵的乘法时,也就是依次进行两个变换时,李代数上对应会发生怎样的变化呢?
S E ( 3 ) SE(3) SE(3)是 s e ( 3 ) \mathcal{se}(3) se(3)的指数映射,那么
e x p ( ξ 1 ∧ ) e x p ( ξ 2 ∧ ) exp(\xi_1^\wedge)exp(\xi_2^\wedge) exp(ξ1∧)exp(ξ2∧)是否等于 e x p ( ( ξ 1 + ξ 2 ) ∧ ) exp((\xi_1+\xi_2)^\wedge) exp((ξ1+ξ2)∧)呢?对于矩阵的指数运算,上式并不成立。
两个李代数指数映射乘积的完整形式,由Baker-Campbell-Hausdorff(BCH)公式给出,
l n ( e x p ( A ) e x p ( B ) ) = A + B + 1 2 [ A , B ] + 1 12 [ A , [ A , B ] ] − 1 12 [ B , [ A , B ] ] + . . . ln(exp(A)exp(B))=A+B+\frac{1}{2}[A,B]+\frac{1}{12}[A,[A,B]]-\frac{1}{12}[B,[A,B]]+... ln(exp(A)exp(B))=A+B+21[A,B]+121[A,[A,B]]−121[B,[A,B]]+...
[,]是李括号,表示二元运算。
以旋转矩阵组成的特殊正交群 S O ( 3 ) SO(3) SO(3)为例,
考虑 S O ( 3 ) SO(3) SO(3)上的李代数 ( l n ( e x p ( ϕ 1 ∧ ) ( ϕ 2 ∧ ) ) ) ∧ (ln(exp(\phi_1^\wedge)(\phi_2^\wedge)))^\wedge (ln(exp(ϕ1∧)(ϕ2∧)))∧,当 ϕ 1 \phi_1 ϕ1或 ϕ 2 \phi_2 ϕ2为小量,BCH公式中李括号二次以上的项可以忽略掉,则可得近似线性表示为,
( l n ( e x p ( ϕ 1 ∧ ) ( ϕ 2 ∧ ) ) ) ∨ ≈ { J l ( ϕ 2 ) − 1 ϕ 1 + ϕ 2 ϕ 1 为小量 J r ( ϕ 1 ) − 1 ϕ 2 + ϕ 1 ϕ 2 为小量 (ln(exp(\phi_1^\wedge)(\phi_2^\wedge)))^\vee\approx\left\{\begin{matrix} J_l(\phi_2)^{-1}\phi_1 +\phi_2 & \phi_1为小量\\ J_r(\phi_1)^{-1}\phi_2 +\phi_1 & \phi_2为小量 \end{matrix}\right. (ln(exp(ϕ1∧)(ϕ2∧)))∨≈{Jl(ϕ2)−1ϕ1+ϕ2Jr(ϕ1)−1ϕ2+ϕ1ϕ1为小量ϕ2为小量
上面公式中第一种相当于是对原旋转矩阵左乘一个微小变换矩阵,第二种相当于是对原旋转矩阵右乘一个微小变换矩阵。乘以微小变换矩阵相当于是发生了微小的位移和姿态变化。
左乘微小变换矩阵的近似雅可比矩阵 J l J_l Jl同推导 s e ( 3 ) \mathcal{se}(3) se(3)的指数映射中作用在平移向量 ρ \rho ρ上的雅可比 J J J
J l = J = s i n θ θ I + ( 1 − s i n θ θ ) a a T + 1 − c o s θ θ a ∧ J_l=J=\frac{sin\theta}{\theta}I+(1-\frac{sin\theta}{\theta})aa^T+\frac{1-cos\theta}{\theta}a^\wedge Jl=J=θsinθI+(1−θsinθ)aaT+θ1−cosθa∧。
通过上面的推导就建立了李群乘法和李代数加法之间的关系。
以旋转矩阵为例,对某个旋转 R R R,其对应的李代数为 ϕ \phi ϕ,对其左乘一个微小旋转 △ R \triangle R △R,其对应的李代数为 △ ϕ \triangle \phi △ϕ。那么在李群上的变化就为 △ R R \triangle R R △RR,而对应的在李代数的变化根据BCH公式近似就为 J l − 1 ( ϕ ) △ ϕ + ϕ J_l^{-1}(\phi)\triangle\phi+\phi Jl−1(ϕ)△ϕ+ϕ,综合以上可以写成:
e x p ( △ ϕ ∧ ) e x p ( ϕ ∧ ) = e x p ( ( ϕ + J l − 1 ( ϕ ) △ ϕ ) ) exp(\triangle \phi^\wedge)exp(\phi^\wedge)=exp((\phi+J_l^{-1}(\phi)\triangle \phi)) exp(△ϕ∧)exp(ϕ∧)=exp((ϕ+Jl−1(ϕ)△ϕ))
上面公式中,如果左乘的微小旋转矩阵对应的李代数带雅可比矩阵,则上式就变为(以左乘为例):
e x p ( ( J l ( ϕ ) △ ϕ ) ∧ ) e x p ( ϕ ∧ ) = e x p ( ( ϕ + J l − 1 ( ϕ ) J l ( ϕ ) △ ϕ ) ∧ ) = e x p ( ( ϕ + △ ϕ ) ∧ ) exp((J_l(\phi)\triangle \phi)^\wedge)exp(\phi^\wedge)=exp((\phi+J_l^{-1}(\phi)J_l(\phi)\triangle \phi)^\wedge)=exp((\phi+\triangle \phi)^\wedge) exp((Jl(ϕ)△ϕ)∧)exp(ϕ∧)=exp((ϕ+Jl−1(ϕ)Jl(ϕ)△ϕ)∧)=exp((ϕ+△ϕ)∧)
由上,李代数上的加法,可近似为李群上带左或右雅可比的乘法:
e x p ( ( ϕ + △ ϕ ) ∧ ) = e x p ( ( J l ( ϕ ) △ ϕ ) ∧ ) e x p ( ϕ ∧ ) = e x p ( ϕ ∧ ) e x p ( ( J r ( ϕ ) △ ϕ ) ∧ ) exp((\phi+\triangle \phi)^\wedge)=exp((J_l(\phi)\triangle \phi)^\wedge)exp(\phi^\wedge)=exp(\phi^\wedge)exp((J_r(\phi)\triangle \phi)^\wedge) exp((ϕ+△ϕ)∧)=exp((Jl(ϕ)△ϕ)∧)exp(ϕ∧)=exp(ϕ∧)exp((Jr(ϕ)△ϕ)∧)
因为旋转矩阵组成的李群各个变换之间只定义了有意义的乘法而没有定义有意义的加法,因此不能直接在李群上定义导数。
而考虑李群与李代数之间的关系,以旋转矩阵为例对 S O ( 3 ) SO(3) SO(3)上的李代数求导,
∂ R P ∂ R \frac{\partial RP}{\partial R} ∂R∂RP
由于 S O ( 3 ) SO(3) SO(3)上只对乘法满足封闭性,因此不能按照常规的微分定义来求导,设 R R R对应的李代数为 ϕ \phi ϕ,由 R = e x p ( ϕ ∧ ) R=exp(\phi^\wedge) R=exp(ϕ∧)可得
∂ e x p ( ϕ ∧ ) P ∂ ϕ = lim δ ϕ → 0 e x p ( ( ϕ + δ ϕ ) ∧ ) p − e x p ( ϕ ∧ ) p δ ϕ = lim δ ϕ → 0 e x p ( J l ( ϕ ) δ ϕ ) ∧ ) e x p ( ϕ ∧ ) p − e x p ( ϕ ∧ ) p δ ϕ = lim δ ϕ → 0 ( I + ( J l ( ϕ ) δ ϕ ) ∧ ) e x p ( ϕ ∧ ) p − e x p ( ϕ ∧ ) p δ ϕ = lim δ ϕ → 0 ( J l ( ϕ ) δ ϕ ) ∧ e x p ( ϕ ∧ ) p δ ϕ = lim δ ϕ → 0 − ( e x p ( ϕ ∧ ) p ) ∧ J l ( ϕ ) δ ϕ δ ϕ = − ( R p ) ∧ J l ( ϕ ) \begin{align}\frac{\partial exp(\phi^\wedge)P}{\partial \phi}&=\lim_{\delta\phi\to 0}\frac{exp((\phi+\delta \phi)^\wedge)p-exp(\phi^\wedge)p}{\delta\phi}\\ &=\lim_{\delta\phi\to 0}\frac{exp(J_l(\phi)\delta \phi)^\wedge)exp(\phi^\wedge)p-exp(\phi^\wedge)p}{\delta\phi}\\ &=\lim_{\delta\phi\to 0}\frac{(I+(J_l(\phi)\delta \phi)^\wedge)exp(\phi^\wedge)p-exp(\phi^\wedge)p}{\delta\phi}\\ &=\lim_{\delta\phi\to 0}\frac{(J_l(\phi)\delta \phi)^\wedge exp(\phi^\wedge)p}{\delta\phi}\\ &=\lim_{\delta\phi\to 0}\frac{-(exp(\phi^\wedge)p)^\wedge J_l(\phi)\delta \phi}{\delta\phi}\\ &=-(Rp)^\wedge J_l(\phi)\end{align} ∂ϕ∂exp(ϕ∧)P=δϕ→0limδϕexp((ϕ+δϕ)∧)p−exp(ϕ∧)p=δϕ→0limδϕexp(Jl(ϕ)δϕ)∧)exp(ϕ∧)p−exp(ϕ∧)p=δϕ→0limδϕ(I+(Jl(ϕ)δϕ)∧)exp(ϕ∧)p−exp(ϕ∧)p=δϕ→0limδϕ(Jl(ϕ)δϕ)∧exp(ϕ∧)p=δϕ→0limδϕ−(exp(ϕ∧)p)∧Jl(ϕ)δϕ=−(Rp)∧Jl(ϕ)
上面推导过程中1到2用到了BCH近似公式,2到3用到了泰勒公式,4到5用到了反对称矩阵的性质 A = − A T A=-A^T A=−AT,最终得到了旋转后的点相对于旋转矩阵李代数的导数。
通过转换成李代数求导得到的最终的导数包含一个 J l J_l Jl矩阵,其形式和计算过于复杂。另外一种李群求导的方法是扰动模型,对 R R R进行一个左乘或右乘扰动,将结果相对于扰动的变化率作为导数,以左乘扰动 △ R \bigtriangleup R △R为例,其对应的李代数为 φ \varphi φ,推导如下:
∂ R p ∂ R = lim φ → 0 e x p ( φ ∧ ) e x p ( ϕ ∧ ) p − e x p ( ϕ ∧ ) p φ \frac{\partial Rp}{\partial R}=\lim\limits_{\varphi \to 0}\frac{exp(\varphi^\wedge)exp(\phi^\wedge)p-exp(\phi^\wedge)p}{\varphi} ∂R∂Rp=φ→0limφexp(φ∧)exp(ϕ∧)p−exp(ϕ∧)p
该式的求导可写成,
∂ R p ∂ R = lim φ → 0 e x p ( φ ∧ ) e x p ( ϕ ∧ ) p − e x p ( ϕ ∧ ) p φ = lim φ → 0 ( I + φ ∧ ) e x p ( ϕ ∧ ) p − e x p ( ϕ ∧ ) p φ = lim φ → 0 φ ∧ R p φ = lim φ → 0 − ( R p ) ∧ φ φ = − ( R p ) ∧ \begin{align}\frac{\partial Rp}{\partial R}&=\lim\limits_{\varphi \to 0}\frac{exp(\varphi^\wedge)exp(\phi^\wedge)p-exp(\phi^\wedge)p}{\varphi}\\ &=\lim\limits_{\varphi \to 0}\frac{(I+\varphi^\wedge)exp(\phi^\wedge)p-exp(\phi^\wedge)p}{\varphi} \\ &= \lim\limits_{\varphi \to 0}\frac{\varphi^\wedge Rp}{\varphi} = \lim\limits_{\varphi \to 0}\frac{-(Rp)^\wedge \varphi}{\varphi}= -(Rp)^\wedge\end{align} ∂R∂Rp=φ→0limφexp(φ∧)exp(ϕ∧)p−exp(ϕ∧)p=φ→0limφ(I+φ∧)exp(ϕ∧)p−exp(ϕ∧)p=φ→0limφφ∧Rp=φ→0limφ−(Rp)∧φ=−(Rp)∧
相比于对李代数直接求导,省去了一个雅可比 J l J_l Jl的计算。
ICP问题的非线性解法
考虑前面ICP优化的目标函数:
e = min T 1 2 ∑ i n ∣ ∣ p i − T q i ∣ ∣ 2 2 = min ξ 1 2 ∑ i = 1 n ∣ ∣ ( p i − e x p ( ξ ∧ ) q i ) ∣ ∣ 2 2 e = \min\limits_{T}\frac{1}{2}\sum\limits_{i}^n||p_i-Tq_i||_2^2=\min\limits_\xi\frac{1}{2}\sum_{i=1}^{n}||(p_i-exp(\xi^\wedge)q_i)||_2^2 e=Tmin21i∑n∣∣pi−Tqi∣∣22=ξmin21i=1∑n∣∣(pi−exp(ξ∧)qi)∣∣22
ξ \xi ξ是 S E ( 3 ) SE(3) SE(3) T T T对应的李代数。
单个误差项关于位姿的导数,使用李代数的扰动模型可得,
∂ e ∂ ξ = lim δ ξ → 0 e ( δ ξ ⊕ ξ ) − e ( ξ ) δ ξ \frac{\partial e}{\partial \xi}=\lim\limits_{\delta\xi\to 0}\frac{e(\delta\xi\oplus\xi)-e(\xi)}{\delta\xi} ∂ξ∂e=δξ→0limδξe(δξ⊕ξ)−e(ξ)
⊕ \oplus ⊕表示左乘模型
对于n对三维空间中的点 p p p及其投影 q q q,希望计算的相机旋转和平移分别为 R , t R,t R,t其对应的李群为 T T T。对于空间中的一点 p i = [ X i , Y i , Z i ] T p_i=[X_i,Y_i,Z_i]^T pi=[Xi,Yi,Zi]T,其对应的投影点像素坐标为 μ i = [ μ i , v i ] T \mu_i=[\mu_i,v_i]^T μi=[μi,vi]T,根据相机模型,有以下关系,
s i [ μ i v i 1 ] = K T [ X i Y i Z i 1 ] s_i\begin{bmatrix}\mu_i\\v_i\\1 \end{bmatrix}=KT\begin{bmatrix}X_i\\Y_i\\Z_i\\1 \end{bmatrix} si μivi1 =KT XiYiZi1
写成矩阵的形式为:
s i μ i = K T p i s_i\mu_i=KTp_i siμi=KTpi
上式隐含了一次齐次坐标往三维坐标的转换。
对于n对空间点和对应的图像中投影的观测点,要估计相机的位姿,目标函数就是最小化两者之间的误差,
T ∗ = a r g min T 1 2 ∑ i = 1 n ∣ ∣ μ i − 1 s i K T p i ∣ ∣ T^*=arg \min\limits_T\frac{1}{2}\sum\limits_{i=1}^{n}||\mu_i-\frac{1}{s_i}KTp_i|| T∗=argTmin21i=1∑n∣∣μi−si1KTpi∣∣
记通过相机外参变换到相机坐标系下 p p p点对应的点 q q q的坐标为 q = ( T p ) 1 : 3 = [ X ′ , Y ′ , Z ′ ] q=(Tp)_{1:3}=[X',Y',Z'] q=(Tp)1:3=[X′,Y′,Z′]
根据相机模型关于 q q q点有:
s μ = K q s\mu=Kq sμ=Kq
展开有:
[ s μ s v s ] = [ f x 0 c x o f y c y 0 0 1 ] [ X ′ Y ′ Z ′ ] \begin{bmatrix} s\mu\\sv\\s \end{bmatrix}=\begin{bmatrix} f_x&0&c_x\\o&f_y&c_y\\0&0&1 \end{bmatrix}\begin{bmatrix}X'\\Y'\\Z'\end{bmatrix} sμsvs = fxo00fy0cxcy1 X′Y′Z′
重投影误差的左乘扰动求导数为:
∂ e ∂ ξ = ∂ e ∂ q ∂ q ∂ ξ \frac{\partial e}{\partial \xi}=\frac{\partial e}{\partial q}\frac{\partial q}{\partial \xi} ∂ξ∂e=∂q∂e∂ξ∂q
根据目标函数和相机模型的公式有:
∂ e ∂ q = − [ ∂ μ ∂ X ′ ∂ μ ∂ Y ′ ∂ μ ∂ Z ′ ∂ v ∂ X ′ ∂ v ∂ Y ′ ∂ v ∂ Z ′ ] = − [ f x Z ′ 0 − f x X ′ Z ′ 2 0 f y Z ′ − f y Y ′ Z ′ 2 ] \frac{\partial e}{\partial q}=-\begin{bmatrix}\frac{\partial \mu}{\partial X'} & \frac{\partial \mu}{\partial Y'} &\frac{\partial \mu}{\partial Z'}\\ \frac{\partial v}{\partial X'}&\frac{\partial v}{\partial Y'}&\frac{\partial v}{\partial Z'}\end{bmatrix}=-\begin{bmatrix}\frac{f_x}{Z'} & 0 &-\frac{f_xX'}{Z'^2}\\ 0&\frac{f_y}{Z'}&-\frac{f_yY'}{Z'^2}\end{bmatrix} ∂q∂e=−[∂X′∂μ∂X′∂v∂Y′∂μ∂Y′∂v∂Z′∂μ∂Z′∂v]=−[Z′fx00Z′fy−Z′2fxX′−Z′2fyY′]
而第二项为变换后的点关于李代数的导数,
∂ ( T p ) ∂ T = [ I − q ∧ 0 0 ] \frac{\partial(Tp)}{\partial T}=\begin{bmatrix}I&-q^\wedge \\ 0 & 0 \end{bmatrix} ∂T∂(Tp)=[I0−q∧0]
根据 q q q定义取出前三维,
∂ q ∂ T = [ I , − q ∧ ] T \frac{\partial q}{\partial T}=[I,-q^\wedge ]^T ∂T∂q=[I,−q∧]T
最后将两者相乘可以求得 ∂ e ∂ ξ \frac{\partial e}{\partial \xi} ∂ξ∂e。
代码示例
使用G2O求解非线性优化问题,节点就是待求解变量,边是观测数据点。
前面推导的是相机模型的点与三维空间点的PnP问题的求解,对于ICP直接是成对三维点之间的优化,相对于PnP更简单。
定义G2O的顶点和边,
class VertexPose : public g2o::BaseVertex<6, Sophus::SE3d> {public:EIGEN_MAKE_ALIGNED_OPERATOR_NEW;// 设置初始化的更新值 virtual void setToOriginImpl() override { _estimate = Sophus::SE3d();}// left multiplication on SE3virtual void oplusImpl(const double *update) {Eigen::Matrix<double, 6, 1> update_eigen;update_eigen << update[0], update[1], update[2],update[3], update[4], update[5];_estimate = Sophus::SE3d::exp(update_eigen) * _estimate;}virtual bool read(std::istream &in) override {return true;} virtual bool write(std::ostream &out) const override { return true;}};class EdgeProjectXYZRGBDPoseOnly : public g2o::BaseUnaryEdge<3, Eigen::Vector3d, bcv::VertexPose> {public:EIGEN_MAKE_ALIGNED_OPERATOR_NEW;EdgeProjectXYZRGBDPoseOnly(const Eigen::Vector3d &point) : _point(point) {}virtual void computeError() override {const VertexPose* p = static_cast<const VertexPose*> (_vertices[0]);_error = _measurement - p->estimate() * _point;}virtual void linearizeOplus() override {VertexPose *p = static_cast<VertexPose*> (_vertices[0]);Sophus::SE3d T = p->estimate();Eigen::Vector3d xyz_trans = T * _point;_jacobianOplusXi.block<3, 3>(0, 0) = -Eigen::Matrix3d::Identity();_jacobianOplusXi.block<3, 3>(0, 3) = Sophus::SO3d::hat(xyz_trans);}bool read(std::istream &in) { return true; }bool write(std::ostream &out) const { return true; }protected:Eigen::Vector3d _point;};定义求解器:
void ICPSolver::NLOSolver(std::vector<cv::Point3f> &pts1,std::vector<cv::Point3f> &pts2,cv::Mat &R, cv::Mat &t){typedef g2o::BlockSolverX BlockSolverType;typedef g2o::LinearSolverDense<BlockSolverType::PoseMatrixType> LinearSolverType;auto solver = new g2o::OptimizationAlgorithmGaussNewton(g2o::make_unique<BlockSolverType>(g2o::make_unique<LinearSolverType>()));g2o::SparseOptimizer optimizer; // graph modeloptimizer.setAlgorithm(solver); // set solveroptimizer.setVerbose(true); // print infobcv::VertexPose *p = new VertexPose();p->setId(0);p->setEstimate(Sophus::SE3d());optimizer.addVertex(p);// add edgefor(size_t i = 0; i < pts1.size(); i++) {bcv::EdgeProjectXYZRGBDPoseOnly *e = new bcv::EdgeProjectXYZRGBDPoseOnly(Eigen::Vector3d(pts2[i].x, pts2[i].y, pts2[i].z));e->setVertex(0, p);e->setMeasurement(Eigen::Vector3d(pts1[i].x, pts1[i].y, pts1[i].z));e->setInformation(Eigen::Matrix3d::Identity());optimizer.addEdge(e);}auto t1 = std::chrono::system_clock::now();optimizer.initializeOptimization();optimizer.optimize(10);auto t2 = std::chrono::system_clock::now();auto d = std::chrono::duration_cast<std::chrono::milliseconds>(t2 - t1).count();std::cout << "duration: " << d << " ms" << std::endl;std::cout << "after optim:\n";std::cout << "T=\n" << p->estimate().matrix() << std::endl;Eigen::Matrix3d R_ = p->estimate().rotationMatrix();Eigen::Vector3d t_ = p->estimate().translation();std::cout <<"det(R_)=" << R_.determinant() << std::endl;std::cout <<"R_R_^T=" << R_ * R_.transpose() << std::endl;std::cout << "R:\n" << R_ << std::endl;std::cout << "t:\n" << t_ << std::endl;R = (cv::Mat_<double>(3, 3) <<R_(0, 0), R_(0, 1), R_(0, 2),R_(1, 0), R_(1, 1), R_(1, 2),R_(2, 0), R_(2, 1), R_(2, 2));t = (cv::Mat_<double>(3, 1) << t_(0, 0), t_(1, 0), t_(2, 0));}完整可运行代码见https://gitee.com/lx_r/basic_cplusplus_examples
- 1.视觉SLAM十四讲第二版p196-198
相关文章:

4.迭代最近点ICP及非线性优化求解
使用非线性优化方法求解ICP 文章目录 使用非线性优化方法求解ICP前情提要ICP问题回顾对矩阵变量求导数 ICP问题的非线性解法代码示例 欢迎访问个人网络日志🌹🌹知行空间🌹🌹 前情提要 在迭代最近点算法ICP及SVD求解中介绍了ICP问…...
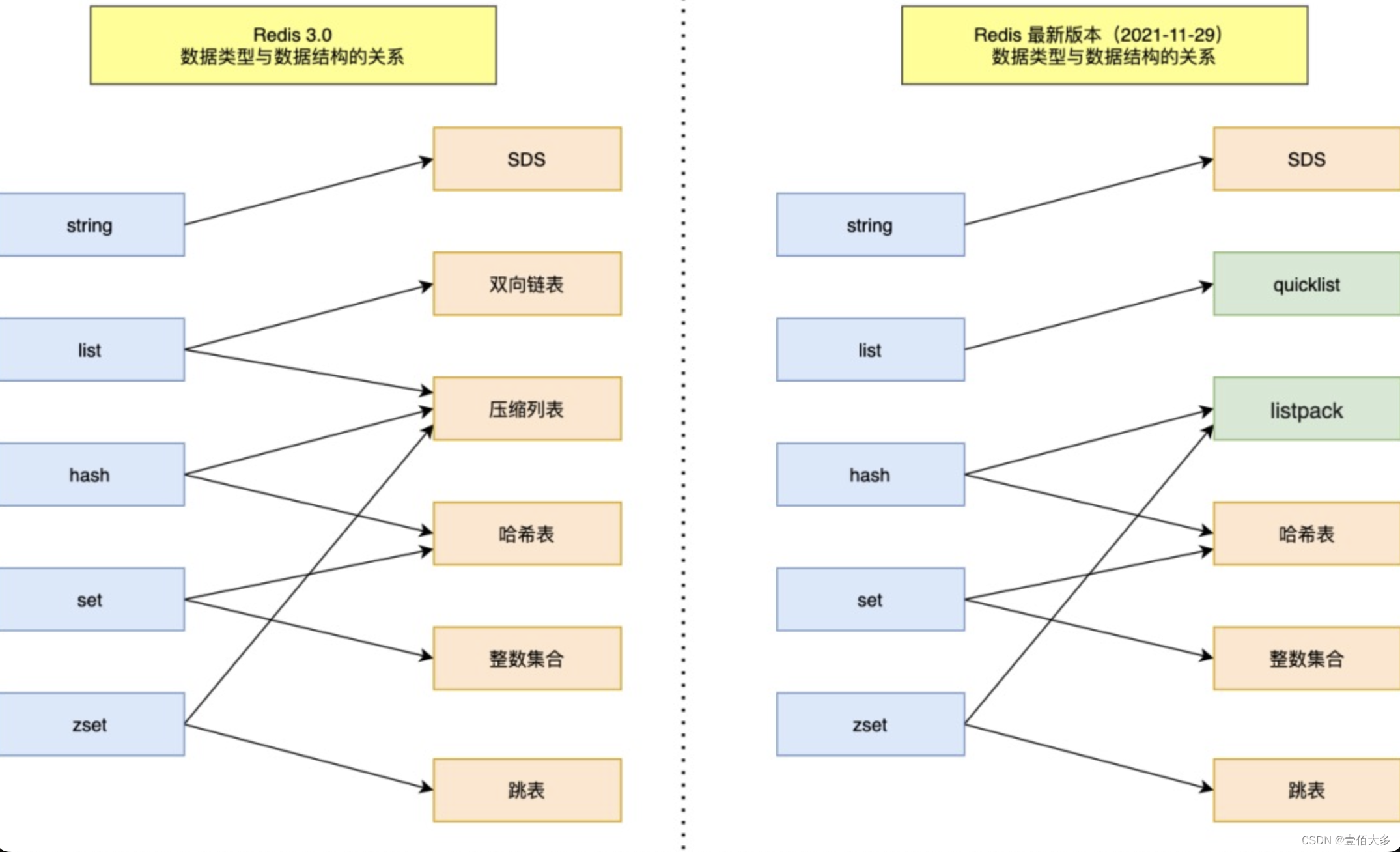
【redis总结】
文章目录 1、redis简介2、为什么要选择redis做缓存3、数据结构4、redis多线程模型redis6.0的变化 5、redis持久化AOF的实现过程RDB的实现过程 6、redis集群的搭建7、 redis过期删除和淘汰策略8、redis的内存淘汰策略 1、redis简介 Redis(Remote Dictionary Server&…...

图数据库:释放关系的力量
【squids.cn】 全网zui低价RDS,免费的迁移工具DBMotion、数据库备份工具DBTwin、SQL开发工具等 在数据管理领域,图数据库已经成为一种强大的工具,它彻底改变了我们处理和分析复杂关系的方式。与依赖表和列的传统关系数据库不同,图…...

Windows系统如何临时关闭“Windows安全中心实时保护”
前言 启动windows depender实时保护可能会使系统不太流畅,也可能会导致我们的程序无法正常运行,因为它会拦截或搜索我们的正常工作。 暂时关闭windows depender的实时保护对许多用户来说非常重要。 一、Win10系统关闭方法 打开Windows安全中心&#…...
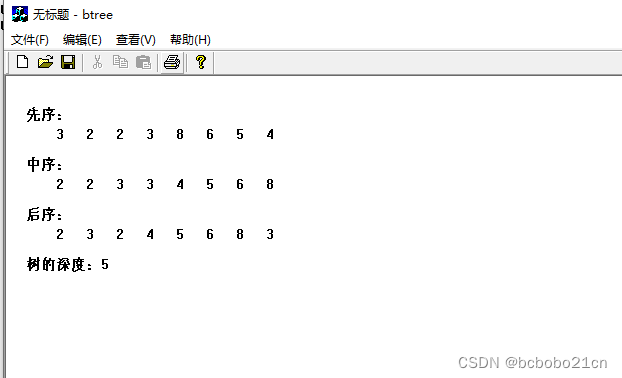
二叉树MFC实现
设有一颗二叉树如下; 这似乎是一颗经常用作示例的二叉树; 对树进行遍历的结果是, 先序为:3、2、2、3、8、6、5、4, 中序为:2、2、3、3、4、5、6、8, 后序为2、3、2、4、5、6、8、3;…...

Nginx之客户并发数限制解读
目录 基本介绍 配置指令 limit_conn_zone limit_conn 其他 limit_rate limit_rate_after limit_req_zone limit_req 基本介绍 在我们进行系统开发设计中,要考虑服务器流量异常,负载过大等问题。对于大流量恶意的攻击访问,会带来带宽…...
白捡一个存储型XSS
本文由掌控安全学院 - 杳若 投稿 起因 利用fofa搜索时发现 org"China Education and Research Network Center" && body"/register" 任意用户注册 在找到该CMS的时候发现存在任意用户注册的情况 http://xxxx.edu.cn/student/Register.ashx …...
转发,重定向和传参)
SpringMVC 学习(五)转发,重定向和传参
6. 转发和重定向 Spring MVC 的底层是 servlet,因此在 Spring MVC 中也存在转发和重定向的概念。 对于转发而言,其目的页面可以在 WEB-INF 目录下。重定向的目的页面不允许在 WEB-INF 目录下,因为重定向相当于用户再次发起一次请求…...
selenium不定位元素直接使用键盘操作(如弹框操作)
今天在使用selenium进行定位时,发现直接定位不了chrome的弹框,如这种弹框: 使用的是下面这行代码 driver.switch_to.alert.accept() 运行报错,说是没有 alert windown。。。。 啊?难道chrome的弹框不是用alert写的&…...
Inno Setup安装中文语言
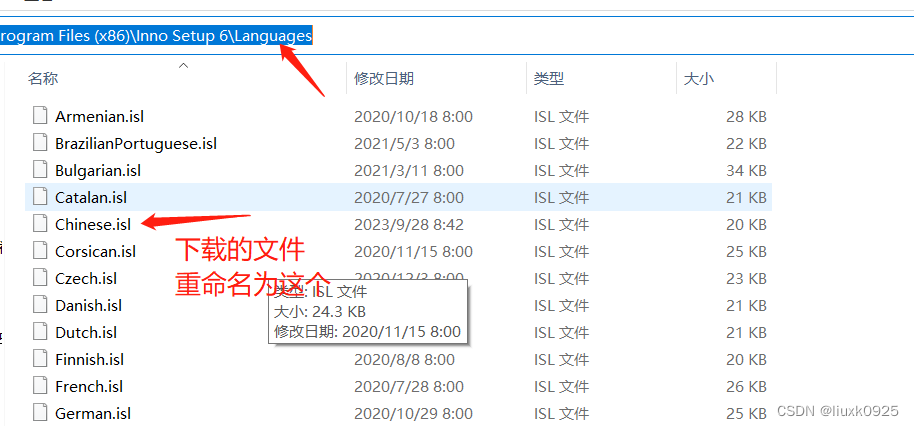
以版本6.2.2为例: 默认安装的Inno Setup是不支持中文语言的,需要我们自行下载安装。 一、打开官网Inno Setup Translations (jrsoftware.org) 下载的文件如下 二、然后重命名放到Inno Setup的如下安装目录中 三、然后重启Inno Setup即可。 打包后的…...

【数据库——MySQL】(10)视图和索引
目录 1. 视图1.1 创建视图1.2 查询视图 2. 索引2.1 索引的分类2.2 索引的建立 参考书籍 1. 视图 1.1 创建视图 基础语法: CREATE [OR REPLACE] VIEW 视图名[(列名表)]ASSELECT语句[WITH CHECK OPTION]说明: 在默认情况下,将在当前数据库创…...
No servers available for service: renren…。 Gateway 网关报503错误 ,已解决
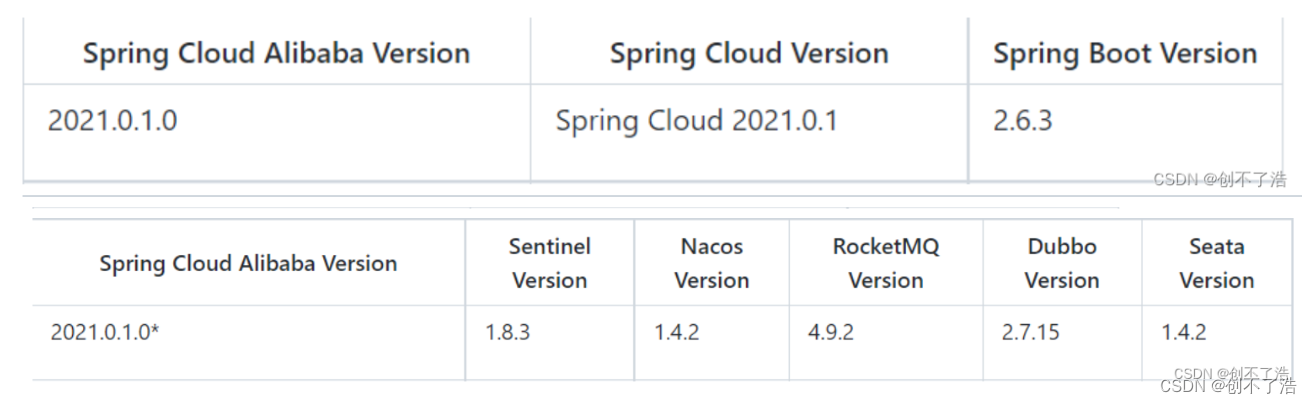
目录 环境配置问题描述loadbalancer的作用 环境配置 问题描述 配置spring cloud gateway使用端口访问就可以,使用lb:// 就报503 gateway:routes:- id: admin_routeuri: lb://gulimall-admin # uri: http://localhost:8080predicates:- Path/api/**filter…...
【Spring Cloud】深入理解 Eureka 注册中心的原理、服务的注册与发现
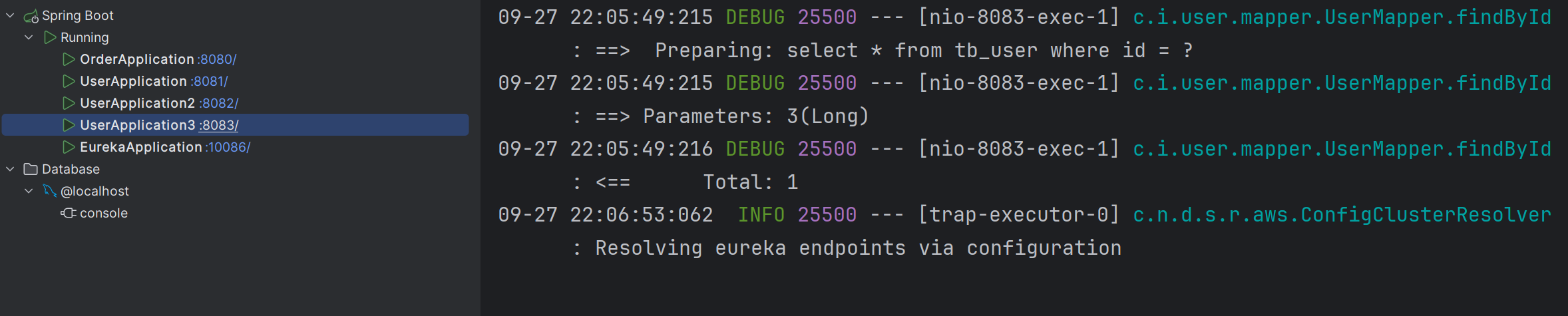
文章目录 前言一、微服务调用出现的问题1.1 服务消费者如何获取服务提供者的地址信息?1.2 如果有多个服务提供者,消费者该如何选择?1.3 消费者如何得知服务提供者的健康状态? 二、什么是 Eureka2.1 Eureka 的核心概念2.2 Eureka 的…...

添加路径到头文件默认搜索路径
在linux环境下写代码,出现函数是从其他文件引用的,需要把该文件的搜索路径添加到当前文件。 注意,除非必要,一般不建议这样做。比较好的方式是写入到CMakeLists或者Makefile中。 一次性生效,命令行输入即可ÿ…...

掌动智能:替代JMeter的压力测试工具有哪些
JMeter是一个广泛使用的开源压力测试工具,但在实际应用中,也有一些其他优秀的替代品可供选择。本文将介绍几个可替代JMeter的压力测试工具,它们在功能、性能和易用性方面都具有独特优势,可以满足不同压力测试需求的选择。 一、Gat…...
Casper Network 构建企业级区块链生态的野望
Casper Network 是基于 Layer1 且图灵完备 Wasm 的智能合约平台,它由唯一可操作的 CBC-Casper Proof-of-Stake (PoS) 共识算法(称为 Highway)支持,该网络是一个无需许可、去中心化的公共区块链。 Casper Network 主网在 2021 年 4…...
TiDB 7.1.0 LTS 特性解读丨关于资源管控 (Resource Control) 应该知道的 6 件事
TiDB 7.1.0 LTS 在前段时间发布,相信很多同学都已经抢先使用了起来,甚至都已然经过一系列验证推向了生产环境。面对 TiDB 7.1 若干重要特性,新 GA 的资源管控 (Resource Control) 是必须要充分理解、测试的一个重量级特性。对于常年奋斗在一线…...
Django Web开发入门基础
官方有很详细的文档,但是看过几遍之后如果要翻找还是有点麻烦,本文算作是学习笔记,提取一些关键点记录下来,另附上官方教程 编写你的第一个 Django 应用 注: 文中的指令使用py,是在Windows上,ma…...
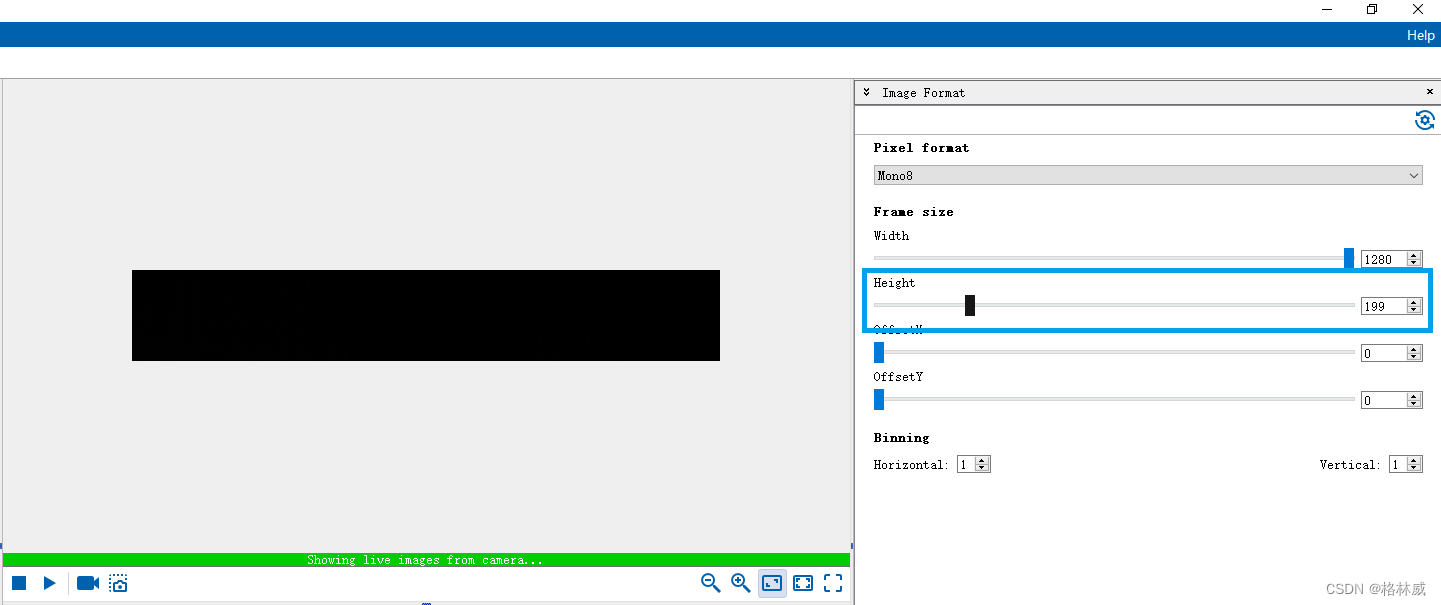
Baumer工业相机堡盟工业相机如何通过BGAPI SDK设置相机的图像剪切(ROI)功能(C#)
Baumer工业相机堡盟工业相机如何通过BGAPI SDK设置相机的图像剪切(ROI)功能(C#) Baumer工业相机Baumer工业相机的图像剪切(ROI)功能的技术背景CameraExplorer如何使用图像剪切(ROI)功…...

LetCode算法题---第2天
注:大佬解答来自LetCode官方题解 80.删除有序数组的重复项Ⅱ 1.题目 2.个人解答 var removeDuplicates function (nums) {let res [];for (let index 0; index < nums.length; index) {let num 0;if (res.includes(nums[index])) {for (let i 0; i < res.length; …...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...

Yolov8 目标检测蒸馏学习记录
yolov8系列模型蒸馏基本流程,代码下载:这里本人提交了一个demo:djdll/Yolov8_Distillation: Yolov8轻量化_蒸馏代码实现 在轻量化模型设计中,**知识蒸馏(Knowledge Distillation)**被广泛应用,作为提升模型…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...

基于Springboot+Vue的办公管理系统
角色: 管理员、员工 技术: 后端: SpringBoot, Vue2, MySQL, Mybatis-Plus 前端: Vue2, Element-UI, Axios, Echarts, Vue-Router 核心功能: 该办公管理系统是一个综合性的企业内部管理平台,旨在提升企业运营效率和员工管理水…...

Golang——6、指针和结构体
指针和结构体 1、指针1.1、指针地址和指针类型1.2、指针取值1.3、new和make 2、结构体2.1、type关键字的使用2.2、结构体的定义和初始化2.3、结构体方法和接收者2.4、给任意类型添加方法2.5、结构体的匿名字段2.6、嵌套结构体2.7、嵌套匿名结构体2.8、结构体的继承 3、结构体与…...

从面试角度回答Android中ContentProvider启动原理
Android中ContentProvider原理的面试角度解析,分为已启动和未启动两种场景: 一、ContentProvider已启动的情况 1. 核心流程 触发条件:当其他组件(如Activity、Service)通过ContentR…...

认识CMake并使用CMake构建自己的第一个项目
1.CMake的作用和优势 跨平台支持:CMake支持多种操作系统和编译器,使用同一份构建配置可以在不同的环境中使用 简化配置:通过CMakeLists.txt文件,用户可以定义项目结构、依赖项、编译选项等,无需手动编写复杂的构建脚本…...

五子棋测试用例
一.项目背景 1.1 项目简介 传统棋类文化的推广 五子棋是一种古老的棋类游戏,有着深厚的文化底蕴。通过将五子棋制作成网页游戏,可以让更多的人了解和接触到这一传统棋类文化。无论是国内还是国外的玩家,都可以通过网页五子棋感受到东方棋类…...
