【数据结构】排序算法(一)—>插入排序、希尔排序、选择排序、堆排序

👀樊梓慕:个人主页
🎥个人专栏:《C语言》《数据结构》《蓝桥杯试题》《LeetCode刷题笔记》《实训项目》
🌝每一个不曾起舞的日子,都是对生命的辜负
目录
前言
1.直接插入排序
2.希尔排序
3.直接选择排序
4.堆排序
前言
本篇文章博主将介绍排序算法中的插入排序:直接插入排序、希尔排序和选择排序:选择排序、堆排序,并进行代码实现,感兴趣的同学给博主点点关注哦🌝
欢迎大家📂收藏📂以便未来做题时可以快速找到思路,巧妙的方法可以事半功倍。
=========================================================================
GITEE相关代码:🌟fanfei_c的仓库🌟
=========================================================================
1.直接插入排序
直接插入排序的思想就是从左到右进行遍历,在遍历过程中将当前的元素插入到前面(已经有序)合适的位置,直到遍历完成。
直接插入排序的特性:
- 元素集合越接近有序,直接插入排序算法时间效率越高;
- 时间复杂度:O(N^2);
- 空间复杂度:O(1);
- 稳定性:稳定。
排序的稳定性:指的是保证排序前2个相等的数其在序列的前后位置顺序和排序后它们两个的前后位置顺序相同。
代码实现:
// 插入排序
void InsertSort(int* a, int n)
{for (int i = 0; i < n-1; i++){int end = i;int tmp = a[end + 1];//保存待插入的值while (end >= 0){if (tmp < a[end]){a[end + 1] = a[end];//向后覆盖}else//因为此时前面已经是有序序列,如果tmp>当前值,证明比前面都大,所以break跳出即可{break;}end--;}a[end+1]= tmp;}
}2.希尔排序
希尔排序与直接插入排序同属插入排序方法,也就是说希尔排序也是靠向前插入的思路进行的。
不同的是,希尔排序先进行预排序,将待排序序列调整的接近有序后,再进行一次直接插入排序。
希尔排序利用了插入排序的特性:待排序序列越接近有序,插入排序时间效率越高。
那么如何进行预排序呢?
希尔排序将待排序序列分组,假设定义一个变量 gap ,那么间隔gap的数据我们分为一组,如图:

预排序阶段:我们以分组情况为基础,每组内部进行直接插入排序,每完成一轮,gap=gap/3-1。
注意:预排序阶段的边界设计很多可以参照直接插入排序,就是将1改为了gap而已,不理解时可以代入直接插入排序进行理解。
直接插入排序阶段:直到gap的值为1的时候,我们发现此时就是直接插入排序了,经过这轮排序就能得到最终的有序序列。


图片取自wikipedia-Shell_sort
希尔排序的特性总结:
- 希尔排序是对直接插入排序的优化。
- 当gap > 1时都是预排序,目的是让数组更接近于有序。当gap == 1时,数组已经接近有序的了,这样就会很快。这样整体而言,可以达到优化的效果。我们实现后可以进行性能测试的对比。
- 希尔排序的时间复杂度不好计算,因为gap的取值方法很多,导致很难去计算,因此在好些树中给出的希尔排序的时间复杂度都不固定。大致为O(N^1.25)到O(1.6*N^1.25)。
- 稳定性:不稳定
代码实现:
// 希尔排序
void ShellSort(int* a, int n)
{int gap = n;while (gap > 1){gap = gap / 3 + 1;//gap递减普遍取这种,也有取gap=gap/2的for (int i = 0; i < n - gap; i++){int end = i;int tmp = a[end + gap];while (end >= 0){if (tmp < a[end]){a[end + gap] = a[end];end -= gap;}else{break;}}a[end + gap] = tmp;}}
}3.直接选择排序
选择排序的思想是每遍历一遍选出最小的值,放到最开始的位置。
我们对该思想优化,每次遍历选出最大值和最小值,分别放到两边。
直接选择排序的特性:
- 直接选择排序思考非常好理解,但是效率不是很好。实际中很少使用
- 时间复杂度:O(N^2)
- 空间复杂度:O(1)
- 稳定性:不稳定
代码实现:
// 选择排序
void SelectSort(int* a, int n)
{int left = 0;int right = n - 1;while (right > left){int maxi = left;int mini = left;for (int i = left+1; i <=right ; i++){if (a[i] > a[maxi]){maxi = i;}if (a[i] < a[mini]){mini = i;}}swap(&a[left], &a[mini]);if (maxi == left)//假设max被换走了,恢复一下{maxi = mini;}swap(&a[right], &a[maxi]);right--;left++;}
}4.堆排序
堆排序首先要介绍的是向下调整算法。
向下调整算法的前提是左右子树是堆。
以小堆为例:
1.给定向下调整的起点(双亲节点下标)和节点总数,根据起点下标计算孩子节点下标。
注意:向下调整时,若有两个孩子节点,则需要确保调整的是较大的孩子节点。
2.比较孩子节点与双亲节点数值大小,若孩子节点小于双亲节点,则交换两者,并将双亲节点的下标更新为之前的孩子节点下标,根据最新的双亲节点下标重新计算孩子节点下标,重复这一过程直到孩子节点超出节点总数。

对于堆排序来说:
以升序为例:
首先构建大堆(推荐使用向下调整),此时堆顶元素一定为最大值,然后将堆顶元素与最后一个节点交换,此时最大值就放到了整个数组的最后面,然后除了最后一个值以外,其他的数据再向下调整,调整完成后堆顶元素为次大值,再与数组倒数第二个位置的值交换,这样依此往复就得到了升序数组。
注意:升序建大堆,降序建小堆。
🌐更多关于堆的内容可以参考博客:堆排序与TopK问题---樊梓慕🌐
堆排序的特性总结:
- 堆排序擅于处理庞大数据。
- 时间复杂度:O(N*logN)
- 空间复杂度:O(1)
- 稳定性:不稳定
代码实现:
// 堆排序
void AdjustDown(int* a, int n, int parent)
{int child = parent * 2 + 1;while (child < n){// 找出小的那个孩子if (child + 1 < n && a[child + 1] > a[child]){++child;}if (a[child] > a[parent]){Swap(&a[child], &a[parent]);// 继续往下调整parent = child;child = parent * 2 + 1;}else{break;}}
}void HeapSort(int* a, int n)
{// 向下调整建堆// O(N)for (int i = (n - 1 - 1) / 2; i >= 0; i--){AdjustDown(a, n, i);}// O(N*logN)int end = n - 1;while (end > 0){Swap(&a[0], &a[end]);AdjustDown(a, end, 0);--end;}
}=========================================================================
如果你对该系列文章有兴趣的话,欢迎持续关注博主动态,博主会持续输出优质内容
🍎博主很需要大家的支持,你的支持是我创作的不竭动力🍎
🌟~ 点赞收藏+关注 ~🌟
=========================================================================
相关文章:

【数据结构】排序算法(一)—>插入排序、希尔排序、选择排序、堆排序
👀樊梓慕:个人主页 🎥个人专栏:《C语言》《数据结构》《蓝桥杯试题》《LeetCode刷题笔记》《实训项目》 🌝每一个不曾起舞的日子,都是对生命的辜负 目录 前言 1.直接插入排序 2.希尔排序 3.直接选择排…...
基于JAVA+SpringBoot的新闻发布平台
✌全网粉丝20W,csdn特邀作者、博客专家、CSDN新星计划导师、java领域优质创作者,博客之星、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ 🍅文末获取项目下载方式🍅 一、项目背景介绍: 随着科技的飞速发展和…...

Java实现word excel ppt模板渲染与导出及预览 LibreOffice jodconverter
Java Office 一、文档格式转换 文档格式转换是office操作中经常需要进行一个操作,例如将docx文档转换成pdf格式。 java在这方面有许多的操作方式,大致可以分为内部调用(无需要安装额外软件),外部调用(需…...

【通意千问】大模型GitHub开源工程学习笔记(2)
使用Transformers来使用模型 如希望使用Qwen-chat进行推理,所需要写的只是如下所示的数行代码。请确保你使用的是最新代码,并指定正确的模型名称和路径,如Qwen/Qwen-7B-Chat和Qwen/Qwen-14B-Chat 这里给出了一段代码 from transformers import AutoModelForCausalLM, Aut…...

MQ - 35 四款MQ的架构设计与实现的对比
文章目录 导图概述RabbitMQ顺序消息定时和延时消息事务消息优先级队列死信队列WebSocketRocketMQ顺序消息定时和延时消息事务消息死信队列消息查询根据 Offset 查询消息根据时间戳查询消息据消息 ID 查询消息SchemaKafka顺序消息幂等事务消息消息查询...
spring6-IOC容器
IOC容器 1、IoC容器1.1、控制反转(IoC)1.2、依赖注入1.3、IoC容器在Spring的实现 2、基于XML管理Bean2.1、搭建子模块spring6-ioc-xml2.2、实验一:获取bean①方式一:根据id获取②方式二:根据类型获取③方式三ÿ…...

macOS - 使用 chromedriver
文章目录 下载对应的 chromedriver 下载 Chrome https://www.google.com/chrome/ 查看 版本 下载对应的 chromedriver http://chromedriver.storage.googleapis.com/index.html https://chromedriver.chromium.org/downloads 移动 sudo mv chromedriver /usr/local/bin/ $ c…...
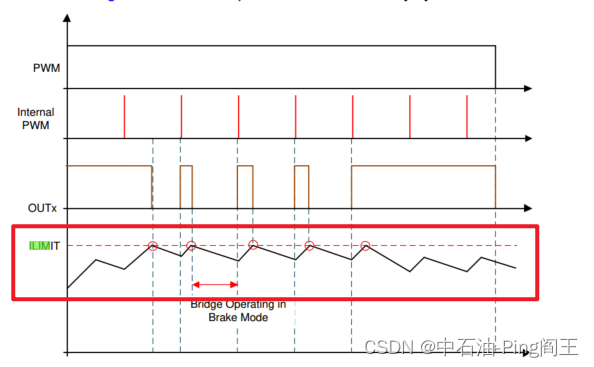
项目进展(四)-双电机均可驱动,配置模拟SPI,调平仪功能初步实现!
一、前言 截止到今天,该项目也算实现基本功能了,后续继续更新有关32位ADC芯片相关的内容,今天对驱动芯片做一个总结,也对模拟SPI做一点总结吧 二、模拟SPI 由于模拟SPI还是得有四种模式(CPOL和CPHA组合为四种),下面…...
)
《学术小白学习之路13》基于DTM和主题共现网络——实现主题时序演化网络分析(数据代码在结尾)
《学术小白学习之路13》基于DTM和主题共现网络实现主题演化网络分析 一、数据导入二、数据预处理2.1分词2.2 向量化三、DTM建模3.1 主题一致性检验3.2主题建模四、计算主题的相似度4.1获取文档主题分布4.2 时期分组4.3相似度计算4.3.1第一时期和第二时期的对比4.3.2第二时期与第…...

实验三十三、三端稳压器 LM7805 稳压性能的研究
一、题目 LM7805 输出电压、电压调整率、电流调整率以及输出纹波电压的研究。 二、仿真电路 电路如图1所示。集成稳压芯片采用 LM7805CT。 三、仿真内容 (1)测量图1(a)LM7805CT 的电压调整率,测量条件为 I O 50…...
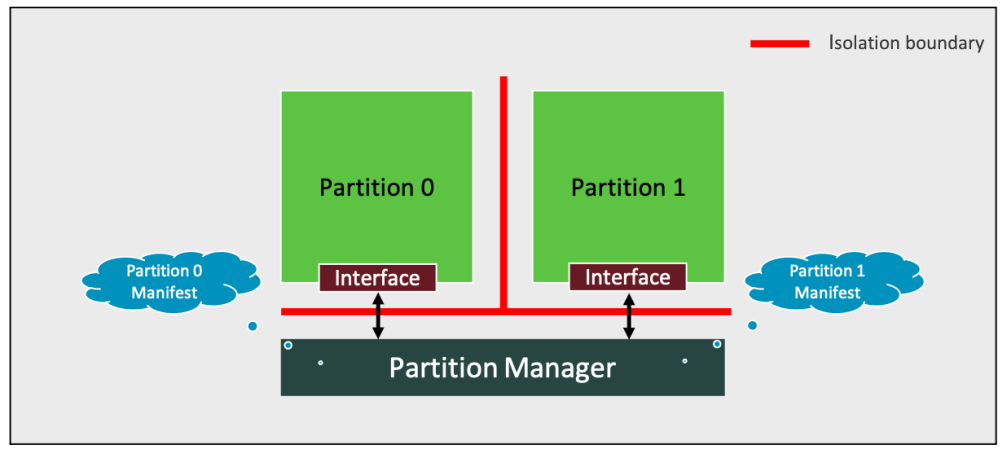
第三章 软件架构
固件框架由如下所示的构建块组成,如上图所示。 隔离边界。分区接口。分区。分区清单。分区管理器。以下各小节详细描述了这些构建块。 3.1 隔离边界 该框架定义了两种类型的隔离边界。 1、逻辑隔离边界,可用于以下情况: (1)通过一个由 IMPLEMENTATION DEFINED 机制定义…...

怎么保护苹果手机移动应用程序ipa中文件安全?
目录 前言 1. 对敏感文件进行文件名称混淆 2. 更改文件的MD5值 3. 增加不可见水印处理 3. 对html,js,css等资源进行压缩 5. 删除可执行文件中的调试信息 前言 ios应用程序存储一些图片,资源,配置信息,甚至敏感数…...

中秋节快乐
中秋节快乐,国庆节快乐...
【记录文】Android自定义Dialog实现圆角对话框
圆角的dialog还是蛮常用的,demo中正好用上了 自定义Dialog,代码中可以设置指定大小与位置 /*** author : jiangxue* date : 2023/9/25 13:21* description :圆角的矩形*/internal class RoundCornerView(context: Context,view: Int, StyleRes theme…...

架构案例2022(四十二)
促销管理系统 某电子商务公司拟升级其会员与促销管理系统,向用户提供个性化服务,提高用户的粘性。在项目立项之初,公司领导层一致认为本次升级的主要目标是提升会员管理方式的灵活性,由于当前用户规模不大,业务也相对…...

kafka 集群搭建 常用命令
1、集群搭建: <1> 将kafka 压缩包解压到某一目录 tar -zxvf kafka_2.12-3.5.1.tgz <2> 修改节点配置文件 vim config/server.properties broker.id0 log.dirs/tmp/kafka-logs <3> 将安装好的kafka 分发到其他服务器 scp -r kafka_2.12-2.4…...
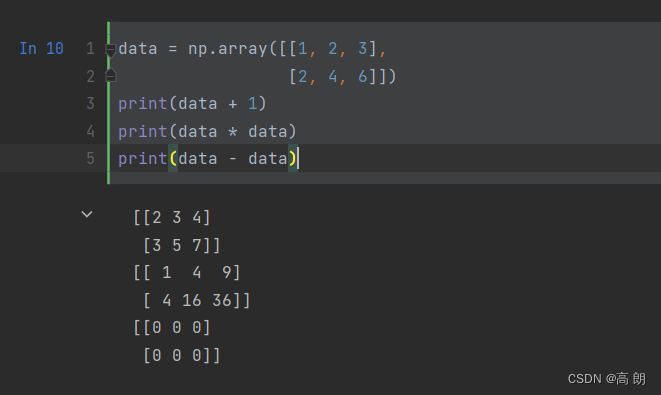
【python】numpy库
文章目录 简单介绍功能示例代码 简单介绍 NumPy(Numerical Python的简称)是Python数值计算最重要的基础包。大多数提供科学计算的包都是用NumPy的数组作为构建基础。 NumPy是在一个连续的内存块中存储数据,独立于其他Python内置对象。NumPy…...
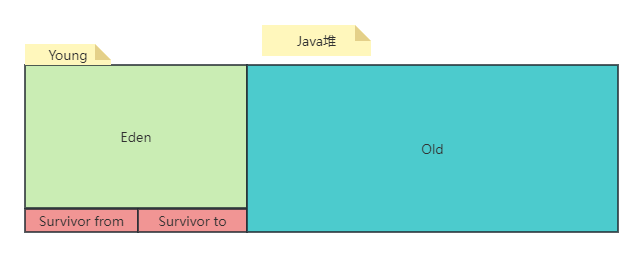
jvm垃圾收集算法
简介 由于《分代收集理论》和不同垃圾收集算法,Java堆应该被划分为不同区域,一般至少会把Java堆划分为新生代(Young Generation)和老年代(Old Generation)两个区域。 垃圾收集器可以只回收其中某一个或者…...
 白皮书)
Arm机密计算架构技术(Armv9 CCA) 白皮书
1. 概述 在本篇文章中,我们将介绍机密计算(Confidential Computing)在现代计算平台中扮演的角色,并解释机密计算的原理。然后我们将说明 Arm 机密计算架构 (Arm CCA) 如何在 Arm 计算平台中实现机密计算。 看完本文后,您将能够: 定义机密计算描述复杂的系统信任链了解R…...
Magisk Delta以及EdXposed工具在逍遥模拟器上安装教程
材料准备: 1,逍遥模拟器 安卓9的镜像 2,EdXpose 的apk以及对应的zip文件 3,riru框架 zip文件 4,magisk delta 的apk文件以及magisk manager的apk文件 放心 这些我都打包放好了,还有已经打包好的逍遥模拟器镜…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...

DeepSeek源码深度解析 × 华为仓颉语言编程精粹——从MoE架构到全场景开发生态
前言 在人工智能技术飞速发展的今天,深度学习与大模型技术已成为推动行业变革的核心驱动力,而高效、灵活的开发工具与编程语言则为技术创新提供了重要支撑。本书以两大前沿技术领域为核心,系统性地呈现了两部深度技术著作的精华:…...
