面试经典算法1:DFS
一、前言
1、题目描述和代码仅供参考,如果有问题欢迎指出
2、解题代码采用acm模式(自己处理输入输出),不采用核心代码模式(只编程核心函数)
3、解题代码采用C++语言(ai一键翻译任意语言,或者cpp转Java等任意语言)
二、题目说明
题目:
给你一个整数集合 nums ,按任意顺序 返回它所有不重复的全排列。
举例:
输入:nums = [1,2,3]
输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
三、DFS回溯法(递归编程实现)
解题思路:
定义一个f()函数求可行的全排列解,如果到叶子节点时该路径可行就记录,否则回溯求解;
f(123) = 1 + f(23),
f(23)= 2 + f(3),
f(3)= 3
解题代码:
#include <iostream>
#include <vector>using namespace std;// end参数可以用nums.size()代替,但是这里为了方便理解所以加上
void permute(vector<int>& nums, int start, int end, vector<vector<int>>& result) {if (start == end) {result.push_back(nums);//到达叶子节点,记录结果return;}for (int i = start; i <= end; i++) {swap(nums[start], nums[i]);// 将第i个元素和第start个元素交换位置,固定第start个元素permute(nums, start + 1, end, result);// 递归调用,固定[start+1, end]这个区间的元素swap(nums[start], nums[i]); // 回溯恢复原来的数组顺序,用于下一次循环}
}int main() {vector<int> nums = { 1, 2, 3 };vector<vector<int>> result;permute(nums, 0, nums.size() - 1, result);for (auto& v : result) {for (int num : v) {cout << num << " ";}cout << endl;}return 0;
}
四、有重复元素时的解法:STL库函数实现
题目说明:
当 nums有重复元素时,如果采用回溯法 ,nums有重复元素就用hash记录被选择的数字,如果已经被选择过就跳过,这当然可以解决问题,不过我们有更优雅的解法,那就是STL中的库函数,这里写出来是因为面试官可能不让你直接调库函数;
解题思路:
两个函数next_permutation和prev_permutation,分别用于生成下一个排列和上一个排列。
next_permutation函数的工作原理是找到从右到左第一个升序对(即nums[i] < nums[i+1]),然后找到这个升序对右边第一个大于它的元素(即nums[j] > nums[i]),交换这两个元素的位置,最后将升序对右边的元素反转。这样就得到了下一个排列。
prev_permutation函数的工作原理类似,只是它是找升序对,然后找到这个升序对左边第一个小于它的元素,交换这两个元素的位置,最后将升序对左边的元素反转。这样就得到了上一个排列。
在main函数中,首先调用prev_permutation函数生成所有的上一个排列,然后调用next_permutation函数生成所有的下一个排列。这样就可以得到所有的排列,而且由于next_permutation函数会跳过所有重复的排列,所以可以避免重复。
原理很详细的一篇文章:https://blog.csdn.net/myRealization/article/details/104803834
解题代码:
#include <iostream>
#include <vector>
#include <algorithm>using namespace std;bool next_permutation(vector<int>& nums) {int i = nums.size() - 2;while (i >= 0 && nums[i] >= nums[i + 1]) --i;if (i == -1) return false;int j = nums.size() - 1;while (nums[j] <= nums[i]) --j;swap(nums[i], nums[j]);reverse(nums.begin() + i + 1, nums.end());return true;
}bool prev_permutation(vector<int>& nums) {int i = 0;while (i < nums.size() - 1 && nums[i] <= nums[i + 1]) ++i;if (i == nums.size() - 1) return false;int j = nums.size() - 1;while (nums[j] >= nums[i]) --j;swap(nums[i], nums[j]);reverse(nums.begin(), nums.begin() + i + 1);return true;
}int main() {vector<int> nums = {1, 2, 3};vector<vector<int>> result;while (prev_permutation(nums)){};//O(n)时间复杂度,而sort是nlog n do {result.push_back(nums);} while (next_permutation(nums));for(auto i: result){for(auto j : i)cout << j << " ";cout << endl;}return 0;
}
如此时间复杂度就是O(n),空间复杂度O(1),如果这样面试还是过不了的话,那就不是你的问题了…
迭代器版本实现
template<typename Iterator>
bool myNextPermutation(Iterator start, Iterator end) { //[start,end)Iterator cur = end - 1, pre = cur - 1; //pre指向partitionNumber while (cur > start && *pre >= *cur) --cur, --pre; //从右到左进行扫描,发现第一个违背非递减趋势的数字if (cur <= start) return false; //整个排列逆序, 不存在更大的排列 //从右到左进行扫描,发现第一个比partitionNumber大的数for (cur = end - 1; *cur <= *pre; --cur); //cur指向changeNumber std::iter_swap(pre, cur);std::reverse(pre + 1, end); //将尾部的逆序变成正序 return true;
}template<typename Iterator>
bool myPrevPermutation(Iterator start, Iterator end) { //[start,end)Iterator cur = end - 1, pre = cur - 1; //pre指向partitionNumber while (cur > start && *pre <= *cur) --cur, --pre; //从右到左进行扫描,发现第一个违背非递增趋势的数字if (cur <= start) return false; //整个排列逆序, 不存在更小的排列 //从右到左进行扫描,发现第一个比partitionNumber小的数for (cur = end - 1; *cur >= *pre; --cur); //cur指向changeNumber std::iter_swap(pre, cur);std::reverse(pre + 1, end); //将尾部的逆序变成正序 return true;
}
1 2 3
从小到大排序的是最小的排列,从大到小排序是最大的排列。
求f(123)的排列,实际上是确定了第1个数以后求len-1个数的排列即 1 + f(23),依次类推毫无疑问这会想到dfs;
然而还有更好的解法
举例 1 3 2,求增长幅度最小下一个排列,
32为逆序不可能减小,所以要换1,1和其右侧第一个大于1的数互换
互换之后此时后半部分是逆序,倒序交换数字的右侧以后就是最小的排列
精简步骤就是
next
1、从右到左找升序对的位置
2、右侧找第一个大于升序对的位置
3、交换,并倒序升序对右侧
prev
1、从左到右找降序对的位置
2、左侧找第一个小于降序对的位置
3、交换,并倒序降序对左侧
为什么不会有重复序列?
因为next_permutation()函数可以生成给定序列的下一个字典序排列。它通过在序列中查找第一个违反字典序排列的元素,并将其交换到序列末尾来实现这一点。
然后,它将序列中剩余的元素重新排序,以生成下一个字典序排列。
由于next_permutation()函数是基于字典序排列的,因此它不会生成重复的序列。这是因为每个元素都只能出现在其原始位置或者在其后面的某个位置上,而
不会出现在其前面的位置上。
举个例子,假设我们有一个序列 [1, 2, 3],它的下一个字典序排列是 [1, 3, 2]。如果我们再次调用next_permutation()函数,它会找到下一个字典序排列,
即 [2, 1, 3]。这个过程会一直持续下去,直到我们回到原始序列为止。
因此,next_permutation()函数可以确保生成的排列是唯一的,不会有重复的序列。
相关文章:

面试经典算法1:DFS
一、前言 1、题目描述和代码仅供参考,如果有问题欢迎指出 2、解题代码采用acm模式(自己处理输入输出),不采用核心代码模式(只编程核心函数) 3、解题代码采用C语言(ai一键翻译任意语言ÿ…...
Windows系统利用cpolar内网穿透搭建Zblog博客网站并实现公网访问内网!
文章目录 1. 前言2. Z-blog网站搭建2.1 XAMPP环境设置2.2 Z-blog安装2.3 Z-blog网页测试2.4 Cpolar安装和注册 3. 本地网页发布3.1. Cpolar云端设置3.2 Cpolar本地设置 4. 公网访问测试5. 结语 1. 前言 想要成为一个合格的技术宅或程序员,自己搭建网站制作网页是绕…...

SmartCode ViewerX VNC 3.11 Crack
SmartCode ViewerX VNC 查看器 ActiveX 轻松地将 VNC 查看器功能添加到您的应用程序中 SmartCode ViewerX VNC Viewer ActiveX 使开发人员可以使用一组直观的 ActiveX 属性和方法完全访问 VNC 查看器功能。借助ViewerX控件,开发人员可以轻松地为其应用程序提供屏幕共…...

傻瓜式Java操作MySQL数据库备份
文章目录 前言存储数据库存储数据表 前言 数据库备份是开发工作中经常要做的事情,好处是mysql提供了一个非常好的命令 mysqldump,直接调用它就可以将数据以sql文件的形式备份出来。但是直接写命令非常不方便,遇到定时备份或者指定备份那么就需…...
redis常用操作命令
日升时奋斗,日落时自省 注:命令区分有点细,择取自己需要的即可 目录 1、单机架构 2、数据库和应用分离 3、分布式基本概念 3.1、应用(Application)/系统(System) 3.2、模块(Module)/组件&…...

pytorch gpu安装
cuda https://blog.csdn.net/qq_51570094/article/details/124148671 https://blog.csdn.net/zxdd2018/article/details/127705627 cudnn https://docs.nvidia.com/deeplearning/cudnn/install-guide/index.html#installlinux-tar 更改cudnn 保证文件目录中只有一个解压后…...

uni跳转页面不缓存上一个页面的方法
一、前言 要实现一个需求,从a页面跳转到b页面,从b页面跳转到c页面,然后按返回,从c页面直接返回a页面(不返回b页面) a->b->c c->a 二、实现方法 前端框架使用的是uni-app,我们修改…...
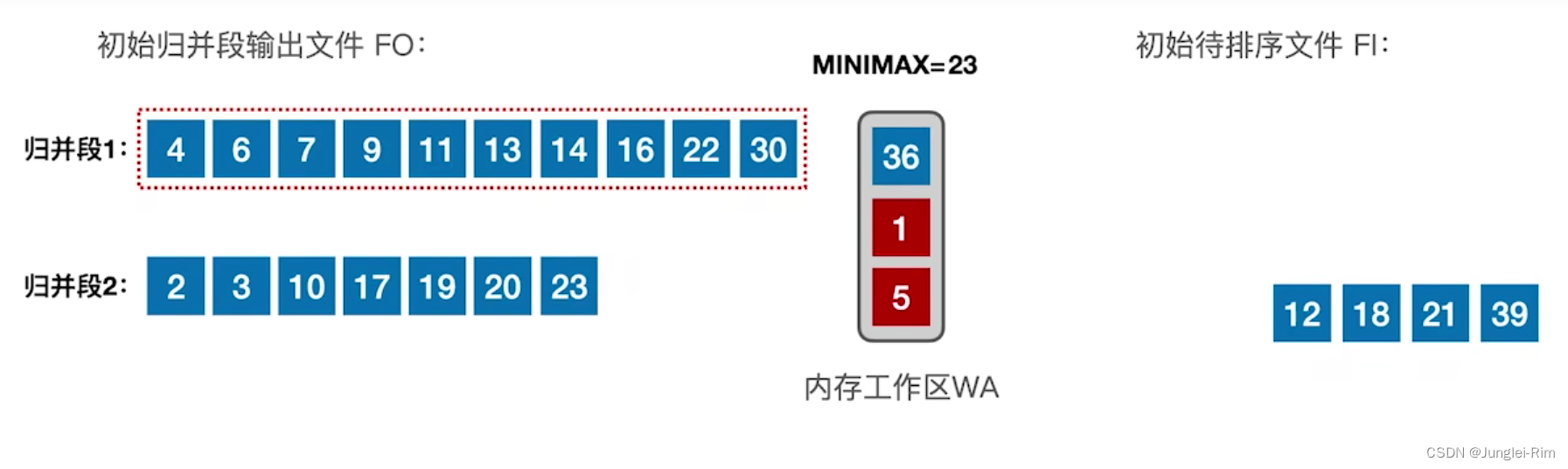
排序:败者树和置换选择排序(解决外部排序中的优化问题)
1.算法目的(败者树) 解决多路平衡归并带来的问题。 在外部排序中,使用k路平衡归并策略, 选出一个最小元素需要对比关键字(k-1)次, 导致内部归并所需时间增加。(可用“败者树”进行优化) 2.败者树的定义 …...

【超分:光谱响应函数】
Spectral Response Function-Guided Deep Optimization-Driven Network for Spectral Super-Resolution (光谱响应函数引导的深度优化驱动网络光谱超分辨) 高光谱图像(HSI)是许多研究工作的关键。光谱超分辨率(SSR&a…...

IoT 物联网 JavaScript 全栈开发,构建家居环境监控系统实战
智能家居环境监测端到端场景,全栈JavaScript开发,串联Ruff硬件、温湿度和空气质量传感器、阿里云 IoT、Serverless函数计算、百度ECharts可视化、最终以微信小程序形式在微信里实时展示家中实时温度,湿度,PM2.5指数。 01 技术架构…...

jupyter notebook可以打开,但无法打开.ipynb文件,报错500 : Internal Server Error
1、错误信息 2、解决办法 打开Anaconda Promt界面,进入自己的虚拟环境。在命令行输入以下指令: pip install --upgrade nbconvert...

latex图片编号+表格编号
对编号重新自定义 \renewcommand{\thefigure}{数字编号x}重新命名图的编号\renewcommand{\thetable}{数字编号x}重新命名表的编号编号含义 平时看书经常看到“图1.2”这样的编号,含义是第1章的第2幅插图;或者“图1.1.2”,含义是第1章第1节的…...

【1day】用友时空KSOA平台 imagefield接口SQL注入漏洞学习
注:该文章来自作者日常学习笔记,请勿利用文章内的相关技术从事非法测试,如因此产生的一切不良后果与作者无关。 目录...

linux之美
linux系统和window系统区别 Linux和Windows是两个不同的操作系统。Linux是一个开源操作系统,而Windows是一个商业操作系统。 Linux可以访问源代码并根据用户的需求进行修改,而Windows无法访问源代码。 Linux是免费的,而Windows是商业操作系…...

5、超链接标签
5、超链接标签 超链接标签就是我们常说的a标签 <a href"path" target"目标窗口位置">连接文本或图像</a> <!-- href(必填项):连接路径 target:连接在哪个窗口打开?是在新页面打开…...

CCF CSP认证历年题目自练 Day15
CCF CSP认证历年题目自练 Day15 题目一 试题编号: 201709-1 试题名称: 打酱油 时间限制: 1.0s 内存限制: 256.0MB 问题描述: 问题描述 小明带着N元钱去买酱油。酱油10块钱一瓶,商家进行促销…...

APP的收费模式及特点
移动应用(APP)的收费模式多种多样,可以根据开发者的需求、目标受众和应用的性质来选择。以下是一些常见的APP收费模式及其特点,希望对大家有所帮助。北京木奇移动技术有限公司,专业的软件外包开发公司,欢迎…...

opencv: 解决保存视频失败的问题
摘要:opencv能读取视频,但保存视频时报错。 一、首先要确保已经下载了openh264.dll文件,否则保存的视频无法打开,详细可以浏览这个:opencv:保存视频。 二、保存视频时出现一下问题: OpenCV:…...
源码编译安装zstd
目录 1 下载源码https://github.com/facebook/zstd 2 解压 3 在解压后的目录里输入make 4 sudo make install 安装完毕 5 输入whereis zstd 检查安装结果 1 下载源码https://github.com/facebook/zstd 2 解压 3 在解压后的目录里输入make 4 sudo make install 安装完毕…...
LabVIEW开发实时自动化多物镜云计算全玻片成像装置
LabVIEW开发实时自动化多物镜云计算全玻片成像装置 数字病理学领域正在迅速发展,这主要是由于计算机处理能力、数据传输速度、软件创新和云存储解决方案方面的技术进步。因此,病理科室不仅将数字成像用于图像存档等简单任务,还用于远程病理学…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...
