机器学习——一元线性回归构造直线,并给出损失函数
目 录
Question
问题分析
1.概念补充
2.流程分析
3.注意
具体实现
最终成果
代码
思考:
Question
在二维平面有n个点,如何画一条直线,使得所有点到该直线距离之和最短
如果能找到,请给出其损失函数
问题分析
1.概念补充
关于损失函数:
也即代价函数,是一个量化误差的表达式
参考链接:线性回归与非线性回归:1.0一元线性回归与代价函数(损失函数)_在一元线性回归中,哪个函数不适用于损失函数(-CSDN博客
本文中我们采用`观测值与实际值差的平方`作为损失函数
具体原理参考链接:知乎形象举例——梯度下降算法
下面是MSE函数,但是我这里就没有除以2了,所以偏导应当有一个2倍
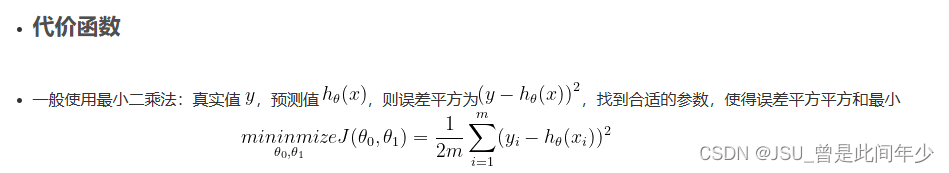
2.流程分析
对于此问题,我们应当按如下步骤进行求解
首先,我们需要对于指定初始的k与b初始化该直线
然后,对学习率(也即步长)和迭代次数进行适当调整
最后,在得到满意的结果后终止调整,整理结果,给出最终参数
3.注意
我们用的并不是直线距离进行损失计算,而是用的△y进行计算,
但是结果并没有影响,因为经过推倒后,距离d与△y成正比
具体实现
本文参考多方资料,使用python代码手写一元线性回归进行求解
计算当前参数下的最小二乘法结果:
def calcLoseFunction(k,b,XData,YData):sum=0for i in range(0,listSize):# 使用偏离值的平方进行累和sum+=(YData[i]-(k*XData[i]+b))**2return sum梯度下降法进行搜索:
#梯度下降法
def calcGradientCorrection(b, k, XData, YData, learningRate, bfsNums):for i in range(0, bfsNums):sumk, sumb = 0, 0for j in range(0, listSize):# 定义预测值Y'normalNum = k * XData[j] + b# 计算逆梯度累和sumk += -(1 / listSize) * (normalNum - YData[j]) * XData[j]sumb += -(1 / listSize) * (normalNum - YData[j])# 在逆梯度的方向上进行下一步搜索k += learningRate * sumkb += learningRate * sumbreturn k, b最终成果
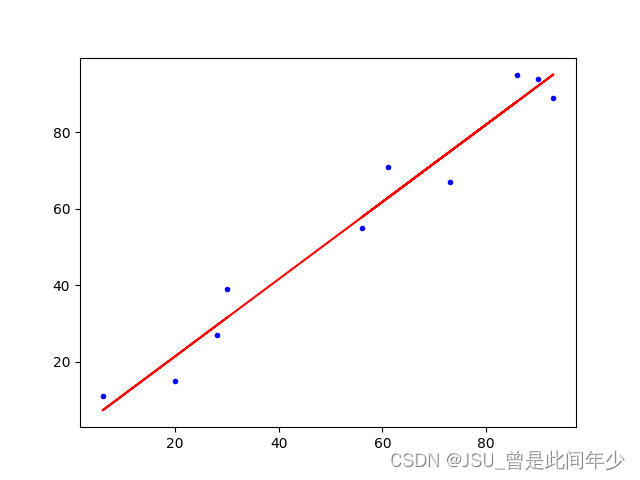
采用随机来对点进行生成,大部分测试较为稳定,模型较为拟合
但是由于X,Y都进行随机生成,按照期望来说,在100*100的矩阵范围内数据呈现均匀分布
于是改造Y数据生成方式为:
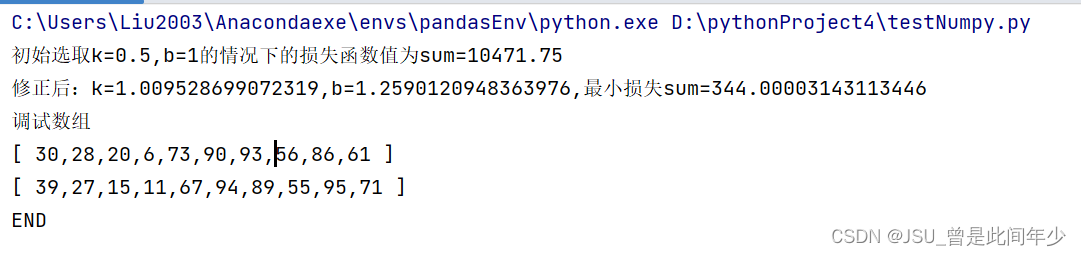
YData=[XData[i]+generateRandomInteger(-10,10) for i in range(listSize) ]调整初始斜率k=0.5进行测试,最终结果较为拟合,效果较好
代码
import numpy #发现直接用List就行了
import random
import matplotlib.pyplot as plt
# random.random()
# random.randint(start,stop)
#################全局数据定义区
# 数组大小
listSize=10
# 定义学习率 取尽量小0.001
learningRate=0.0001
#定义初始直线的 斜率k 和 截距b 45° 1单位距离
# 现在设置 k=0.5 检验程序
k,b=0.5,1
#定义迭代次数
bfsNums=9999
#################全局数据定义区END
# 生成随机数
def generateRandomInteger(start, end):# [1-100]return random.randint(start, end)# 打印本次随机生成的X,Y 便于快速粘贴复现
def printXYArray(XData,YData):# 打印Xprint("[", ",".join([str(i) for i in XData]), "]")# 打印Yprint("[", ",".join([str(i) for i in YData]), "]")# 最小二乘法定义损失函数 并计算
#参考链接:https://blog.csdn.net/zy_505775013/article/details/88683460
# 求最小二乘法的最小值 最终结果应当是在learningRate一定情况下 这个最小的sum
def calcLoseFunction(k,b,XData,YData):sum=0for i in range(0,listSize):# 使用偏离值的平方进行累和sum+=(YData[i]-(k*XData[i]+b))**2return sum#梯度下降法
def calcGradientCorrection(b, k, XData, YData, learningRate, bfsNums):for i in range(0, bfsNums):sumk, sumb = 0, 0for j in range(0, listSize):# 定义预测值Y'normalNum = k * XData[j] + b# 计算逆梯度累和 注意这里求偏导应当是两倍 不知道为什么写成1了# 求MSE的偏导sumk += -(2 / listSize) * (normalNum - YData[j]) * XData[j]sumb += -(2 / listSize) * (normalNum - YData[j])# 在逆梯度的方向上进行下一步搜索k += learningRate * sumkb += learningRate * sumbreturn k, b# 随机生成横坐标
XData=[generateRandomInteger(1,100) for i in range(listSize) ]
# 随机生成纵坐标
YData=[XData[i]+generateRandomInteger(-10,10) for i in range(listSize) ]
# 纯随机生成 但是可视化效果不直观
# YData=[generateRandomInteger(1,100) for i in range(listSize) ]
# 死值替换区
# XData=testArrayX
# YData=testArrayYprint("初始选取k={},b={}的情况下的损失函数值为sum={}".format(k,b,calcLoseFunction(k,b,XData,YData)))
# 对k,b进行梯度修正
k,b=calcGradientCorrection(b,k,XData,YData,learningRate,bfsNums)
print("修正后:k={},b={},最小损失sum={}".format(k,b,calcLoseFunction(k,b, XData, YData)))
print("调试数组")
printXYArray(XData,YData)#画图
plt.plot(XData, YData, 'b.')
plt.plot(XData, k*numpy.array(XData)+b, 'r')
plt.show()
print("END")思考:
如果替换在三维空间会怎么样,如何去求?
答:在三维空间内,我们就需要对三个变量(K1,K2,b)进行偏导求解,然后同样在逆梯度方向上搜索求解。注意要替换对应的损失函数,将直线方程进行替换即可!
相关文章:

机器学习——一元线性回归构造直线,并给出损失函数
目 录 Question 问题分析 1.概念补充 2.流程分析 3.注意 具体实现 最终成果 代码 思考: Question 在二维平面有n个点,如何画一条直线,使得所有点到该直线距离之和最短 如果能找到,请给出其损失函数 问题分析 1.概念…...
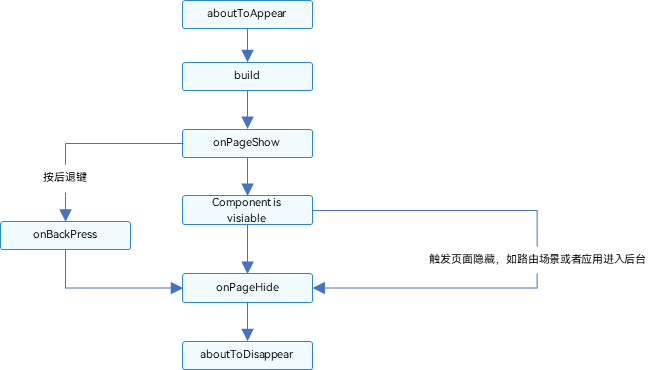
OpenHarmony自定义组件介绍
一、创建自定义组件 在ArkUI中,UI显示的内容均为组件,由框架直接提供的称为系统组件,由开发者定义的称为自定义组件。在进行 UI 界面开发时,通常不是简单的将系统组件进行组合使用,而是需要考虑代码可复用性、业务逻辑…...
云原生之使用Docker部署PDF多功能工具Stirling-PDF
云原生之使用Docker部署PDF多功能工具Stirling-PDF 一、Stirling-PDF介绍1.1 Stirling-PDF简介1.2 Stirling-PDF功能 二、本次实践规划2.1 本地环境规划2.2 本次实践介绍 三、本地环境检查3.1 检查Docker服务状态3.2 检查Docker版本3.3 检查docker compose 版本 四、下载Stirli…...
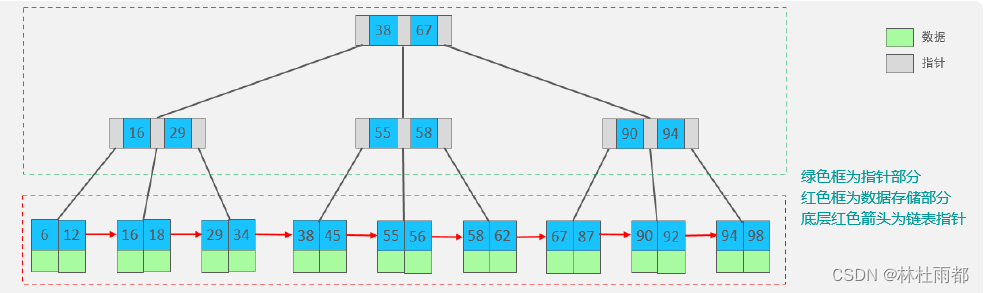
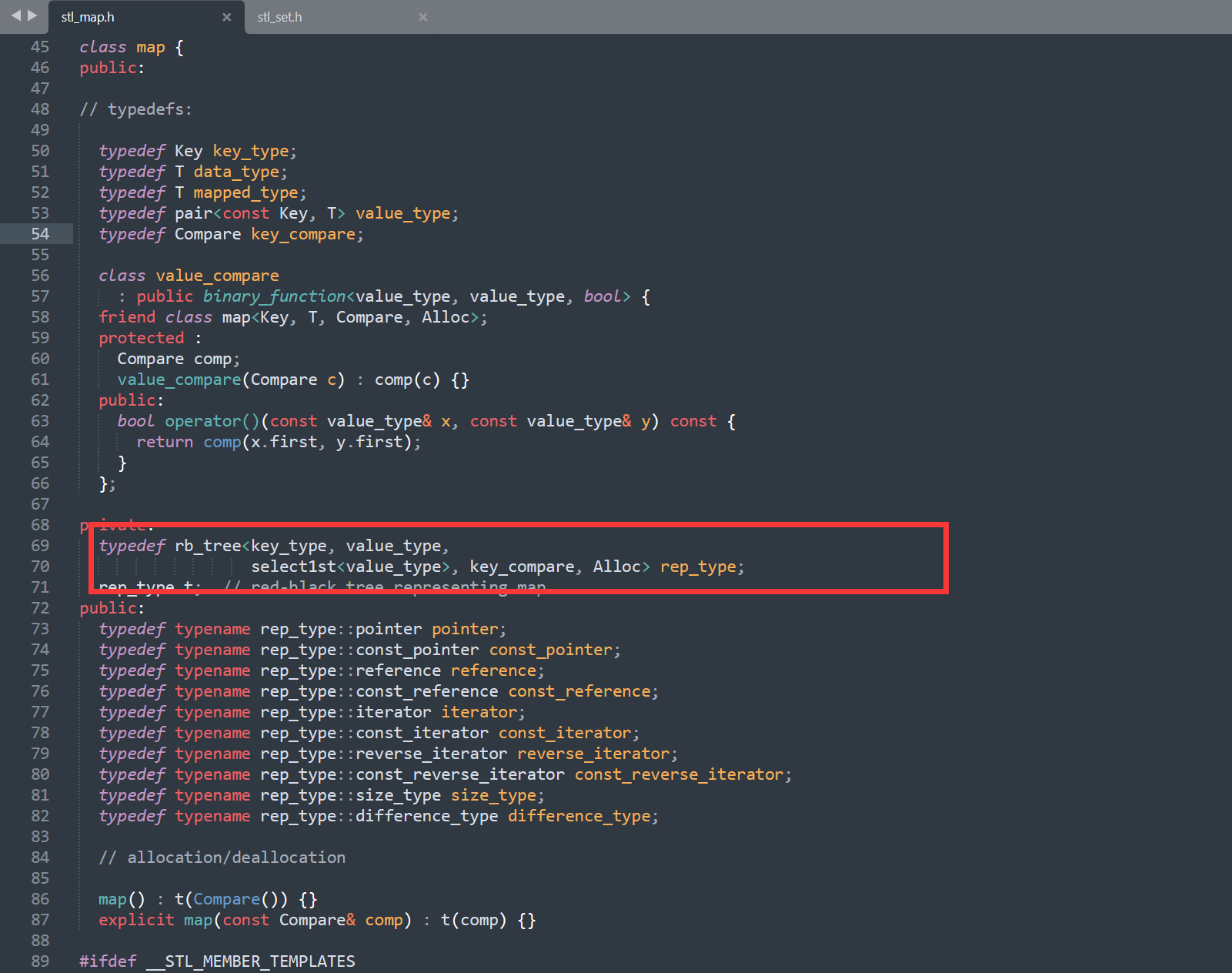
B树和B+树的介绍和对比,以及MySQL为何选择B+树
在计算机科学中,B树和B树是常用的数据结构,用于在大规模数据集上进行高效的插入、删除和查找操作。它们在数据库管理系统、文件系统等许多实际应用中发挥着重要作用。本文将深入介绍B树和B树的结构特点、实际应用方面以及它们的优缺点,并最后…...

MD5 绕过第一式:弱比较绕过
文章目录 参考环境MD5韧性脆弱性md5() 隐式类型转换字符串连接数学运算布尔判断相等运算符 科学计数法科学计数法前缀 0E 与 0e PHP8 与 PHP 其他版本下字符串转化为数值的具体规则PHP8数值字符串优化 其他版本更为详细的讲解 字符串与字符串的弱比较字符串与数值的弱比较0e215…...
红黑树是如何实现的?
文章目录 一、红黑树的概念二、红黑树的性质三、红黑树和AVL树对比四、红黑树的插入1. 红黑树的结点定义2. 父亲的颜色3. 叔叔的颜色为红色4. 叔叔不存在5. 叔叔存在且为黑6. 插入的抽象图 五、红黑树的验证1. 检查平衡2. 计算高度与旋转次数3. 验证 六、 红黑树与AVL树的比较 …...

实验室没人导该怎么办
实验室没人教该怎么办 Q: 国内top5高校研一,课题开始老板就给了一个大方向,之后怎么做实验都是自己看文献研究的,终于开始动手做实验,才发现别人根本不想管你,宁愿抱着电脑看剧也不想教你,十分焦虑,该怎么办? A: 按照大多数实验室的惯例,老板一定会指派一个小老板…...
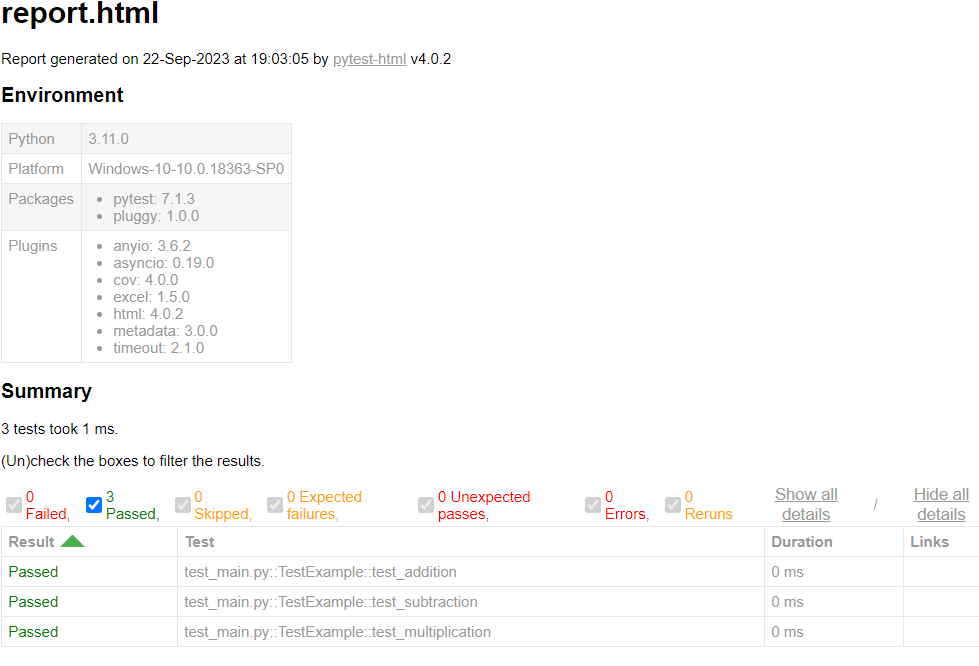
pytest简明教程
1. 简介 pytest是一款基于Python的测试框架。与Python自带的unittest相比,pytes语法更加简洁,断言更加强大,并且在自动测试以及插件生态上比unittest都要更加强大。 1.1. 安装pytest pip install pytest1.2. pytest命名规则 pytest默认会…...

解决方案:解决https页面加载http资源报错
HTTPS页面加载HTTP资源会报错的原因是出于安全性考虑。 HTTPS(HyperText Transfer Protocol Secure)是一种通过使用SSL/TLS加密通信来保护数据传输的协议,它确保了客户端和服务器之间的安全连接。 当HTTPS页面尝试加载非加密的HTTP资源时&a…...
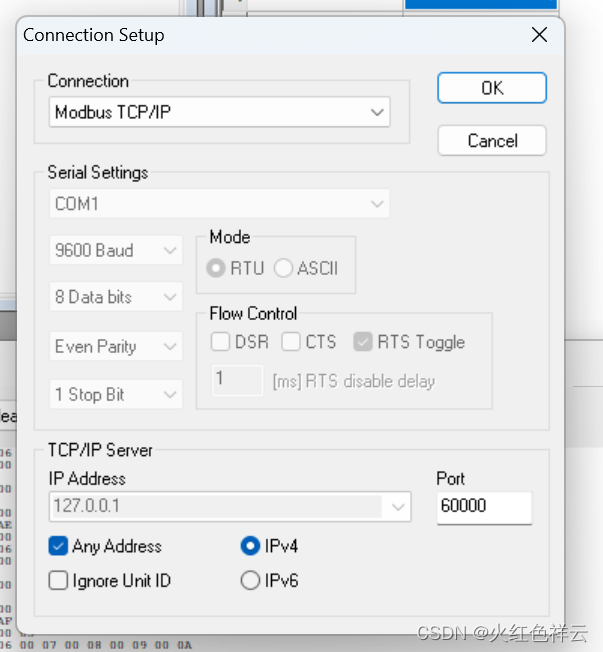
嵌入式开源库之libmodbus学习笔记
socat 安装sudo apt-get install socat创建终端 socat -d -d pty,b115200 pty,b115200查看终端 ls /dev/pts/ minicom 安装 sudo apt-get install minicom链接虚拟终端 sudo minicom -D /dev/pts/3以十六进制显示 minicom -D /dev/pts/1 -H设置波特率 minicom -D /dev/pts/1…...

Spring MVC 中的数据验证技术
一、前言 在Web开发中,数据验证是不可或缺的一部分。Spring MVC 框架提供了强大的数据验证支持,可以帮助我们轻松地对用户提交的数据进行验证。 二、实现 Spring MVC 使用 JSR-303 验证规范(Hibernate Validator 是其参考实现)…...
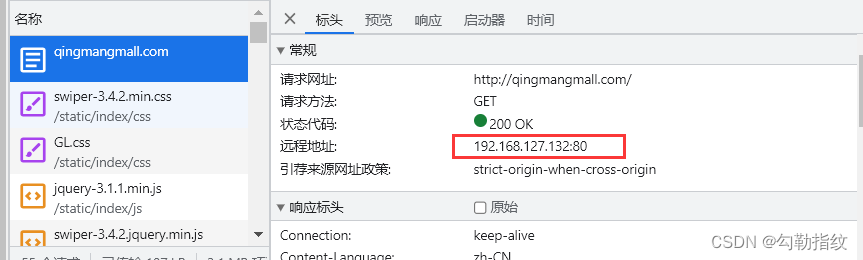
windows 修改hosts映射,可以ping通,但是无法通过http url 路径访问,出现 500 Internal Privoxy Error
问题描述 今天在学习nginx时,想在hosts配置一个nginx的域名映射,但是发现访问nginx服务的ip时可以访问通,在dos命令窗口ping配置的域名映射也可以ping通,但是一旦在浏览器通过http请求访问配置的hosts域名映射时却出现 500 Inter…...

如何将图片转为ico格式
这里主要是记录一个网站,如果你有更好的办法欢迎留言~ ico简介 ICO(Icon)是一种用于表示图标的文件格式,常用于Windows操作系统中。ICO格式的图片通常用于表示应用程序、文件夹、网站等的图标。 ICO文件可以包含多个图标&#x…...

ElasticSearch - 基于 JavaRestClient 操作索引库和文档
目录 一、RestClient操作索引库 1.1、RestClient是什么? 1.2、JavaRestClient 实现创建、删除索引库 1.2.1、前言 1.2.1、初始化 JavaRestClient 1.2.2、创建索引库 1.2.3、判断索引库是否存在 1.2.4、删除索引库 1.3、JavaRestClient 实现文档的 CRUD 1.3…...

【人脸质量评估】MagFace:一个既可以用作人脸识别,又可以用作人脸质量评估的方法
论文题目:《MagFace: A Universal Representation for Face Recognition and Quality Assessment》-CVPR2021 论文地址:https://arxiv.org/abs/2103.06627v4 代码地址:https://github.com/IrvingMeng/MagFace...

FPGA 图像缩放 千兆网 UDP 网络视频传输,基于RTL8211 PHY实现,提供工程和QT上位机源码加技术支持
目录 1、前言版本更新说明免责声明 2、相关方案推荐UDP视频传输--无缩放FPGA图像缩放方案我这里已有的以太网方案 3、设计思路框架视频源选择ADV7611 解码芯片配置及采集动态彩条跨时钟FIFO图像缩放模块详解设计框图代码框图2种插值算法的整合与选择 UDP协议栈UDP视频数据组包U…...
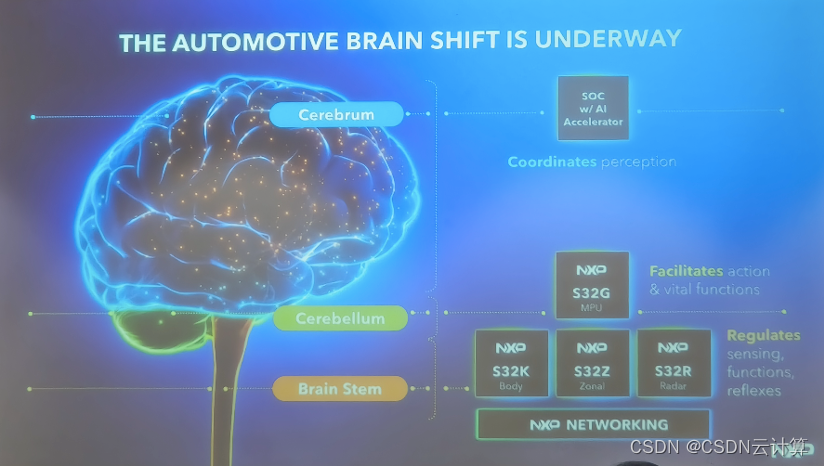
智能驾驶、智能家居、智能工业中的 AI 关键基础设施,半导体厂商恩智浦的角色是什么?
我们来看一条七年前的真实新闻报道,2016 年《福布斯》在报道中提到“2020 年会有 1000 万台的自动驾驶汽车”。然而 2023 年的现在,真正实现 L4 级别自动驾驶的汽车,仍然远远没有达到这个预测的数量。 另一边,数据显示,…...

APScheduler包——python tornado框架中实现定时任务
介绍: APScheduler的全称是Advanced Python Scheduler。它是一个轻量级的 Python 定时任务调度框架。APScheduler 支持三种调度任务:固定时间间隔,固定时间点(日期),Linux 下的 Crontab 命令。同时…...

BASH shell脚本篇3——字符串处理
这篇文章介绍下BASH shell中的字符串处理的相关命令。之前有介绍过shell的其它命令,请参考: BASH shell脚本篇1——基本命令 BASH shell脚本篇2——条件命令 Bash字符串也是一种数据类型,它用于表示文本而不是数字,它是一组可能…...

【SSL】用Certbot生成免费HTTPS证书
1. 实验背景 服务器:CentOS7.x 示例域名: www.example.com 域名对应的web站点目录: /usr/local/openresty/nginx/html 2. 安装docker # yum -y install yum-utils# yum-config-manager --add-repo https://download.docker.com/linux/ce…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...
