课题学习(二)----倾角和方位角的动态测量方法(基于磁场的测量系统)
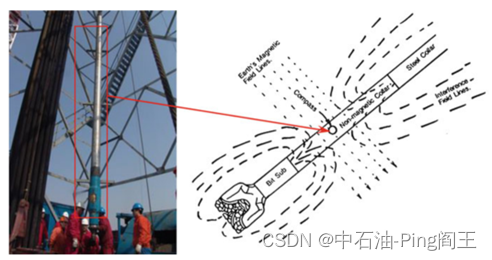
磁性测量工具安装在非磁性钻铤内,如图1,以避免磁性随钻测量工具测量时受到外部干扰。
测量系统采用三轴加速度计和三轴磁通门,并采用冗余设计,由于井下振动剧烈,陀螺仪的可靠性将大大降低。为了保证整个钻井过程中系统的可靠性,我们只以陀螺仪的测量信号作为参考。采用非磁性钻铤将电子测量仪器与上下钻柱的磁场分开,防止传感器处地球磁场的畸变。
当*钻柱旋转时,静态测量的公式不再适用 *。当传感器安装在旋转钻柱的中心时,测量x和y轴信号将呈现正弦波,平均值为零。因此,我们需要开发一套新的公式来满足动态旋转的需要。
当倾角很小时或者趋向于0,cosI=1,sinI=0(此处I为倾角),于是式(1.1)可以写作式(1.2)和(1.3)。(CSDN公式太难打,直接放图)
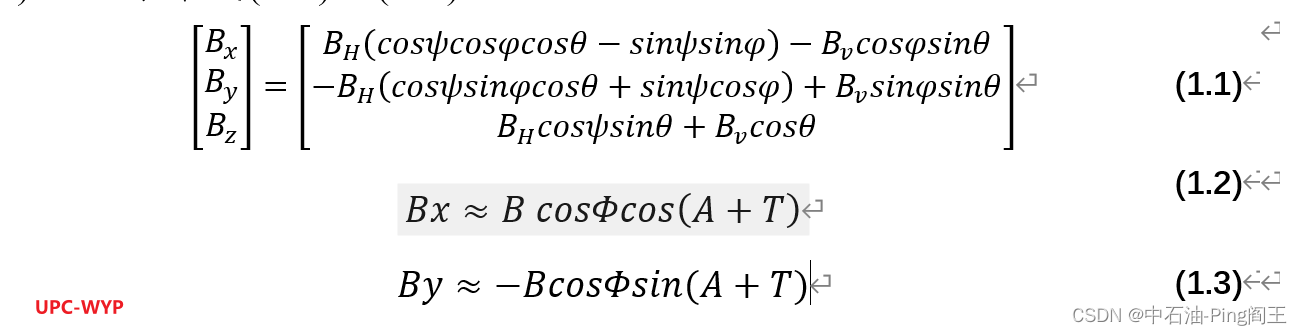
因为倾角比较小,所以Gx,Gy也非常小(几乎垂直,重力在X,Y轴上无分量)由式(1.4)可知,此时的sinI不可以近似为0。
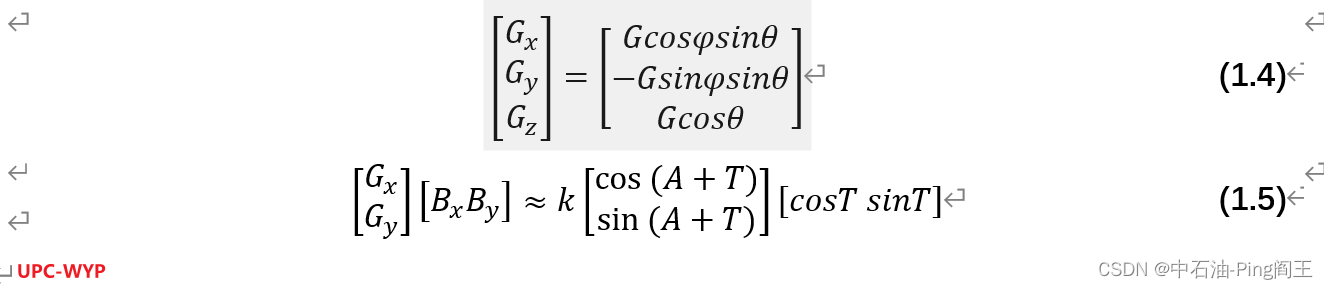
式(1.5)中的k=G∙sinI∙B∙cosΦ,同样sinI也不能看做是0。同样由式(1.5)可以得到式(1.6)(1.7)。
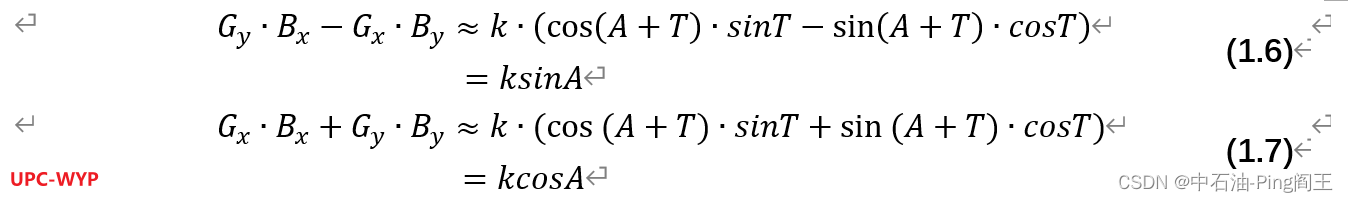
由式(1.6)(1.7)相除之后可得到A_small的值:
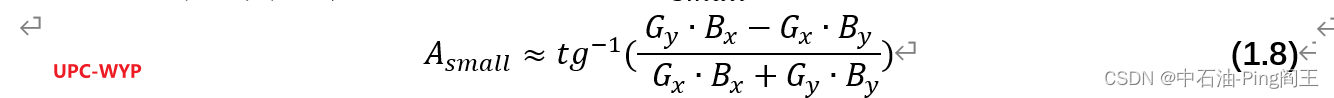
当drillstring旋转时,X和Y轴的重力、磁场分量会呈现出正弦变化的波形,上述公式需要进一步推导:
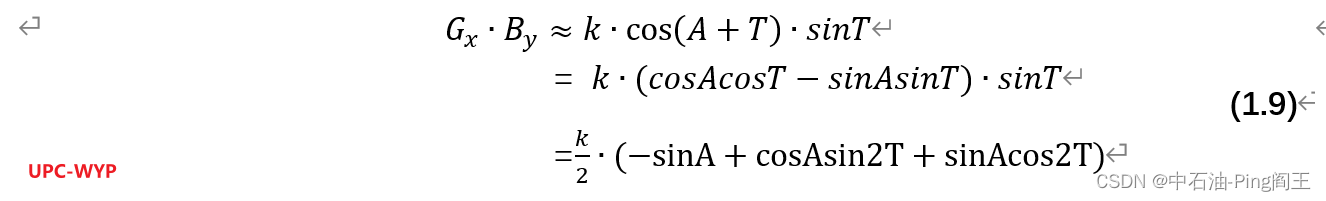
式(1.9)两侧对工具面T积分,得到
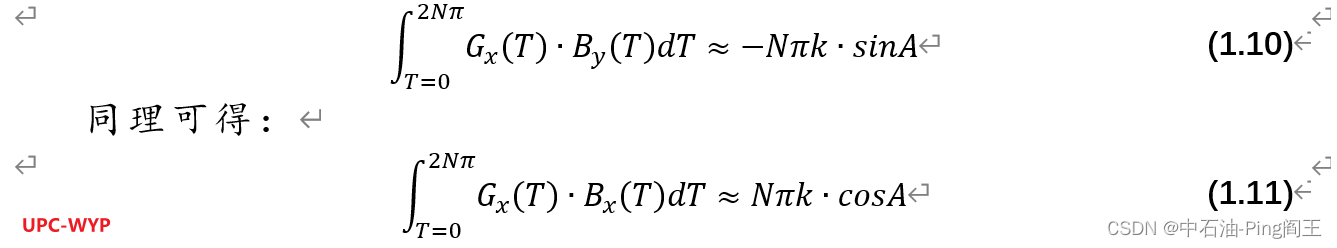
那么当钻柱旋转时,A_small’计算公式如下:
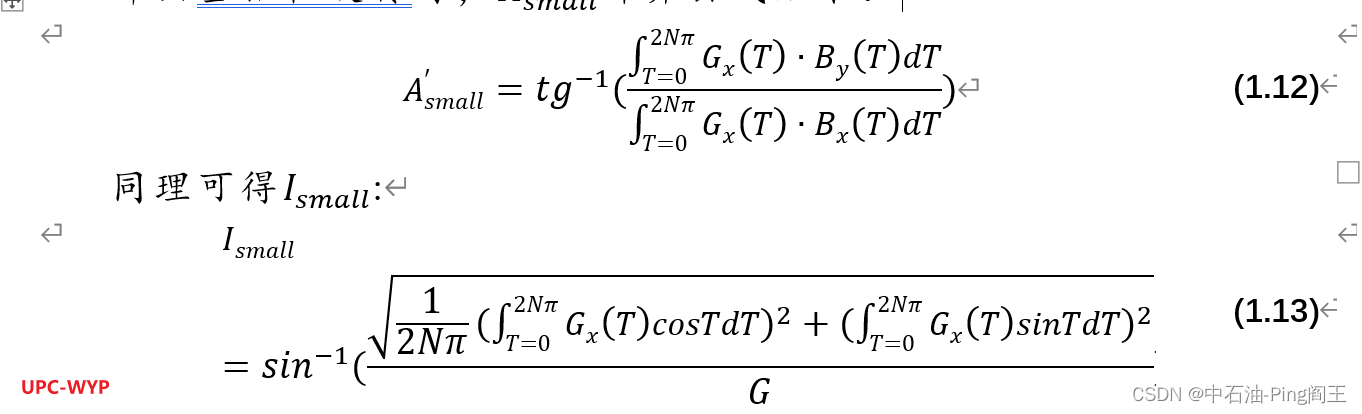
上式中,T为磁工具面角,G为重力加速度。
当倾角从0°到90°变化时,对磁工具面角进行全周期的积分,可得到旋转条件下的另一个连续式,下面计算挠度和方位的两式适用于整个井斜工况:
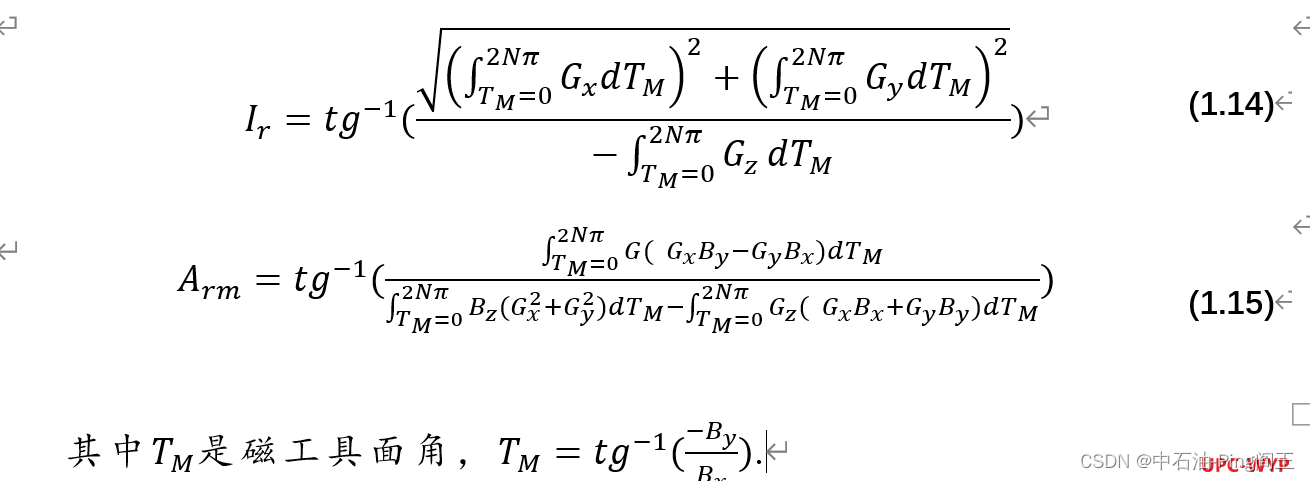
今晚先到这了,后续持续更新。。。
本专栏其他博客:
课题学习(一)----静态测量
相关文章:
课题学习(二)----倾角和方位角的动态测量方法(基于磁场的测量系统)
磁性测量工具安装在非磁性钻铤内,如图1,以避免磁性随钻测量工具测量时受到外部干扰。 测量系统采用三轴加速度计和三轴磁通门,并采用冗余设计,由于井下振动剧烈,陀螺仪的可靠性将大大降低。为了保证整个钻井过程中系统…...
Docker-Windows安装使用
1.下载docker https://cr.console.aliyun.com/cn-hangzhou/instances/mirrors 2.配置虚拟化环境 通过控制面板“设置”启用 Hyper-V 角色 右键单击 Windows 按钮并选择“应用和功能”。选择相关设置下右侧的“程序和功能”。选择“打开或关闭 Windows 功能”。选择“Hyper-…...

在Windows11上安装ubuntu虚拟机
一开始是参考了 VMware17虚拟机安装Ubuntu最新版本(Ubuntu22.04LTS)详细步骤 专栏的1和2来的。但是后面总是提示operating system not found,就参考vmware安装ubuntu时总是提示operating system not found,选择典型安装而不是专栏选择的自定义安装&#…...

【微服务】spring 控制bean加载顺序使用详解
目录 一、前言 二、使用order注解控制顺序 2.1 order 注解使用示例 2.2 order注解顺序失效问题 2.2.1 order失效问题解决办法 2.3 实现Ordered接口 三、使用dependon注解控制顺序 四、AutoConfiguration注解控制bean加载顺序 4.1 AutoConfigureBefore 操作演示 4.2 A…...
python-切换镜像源和使用PyCharm进行第三方开源包安装
文章目录 前言python-切换镜像源和使用PyCharm进行第三方开源包安装1. 切换镜像源2. 使用PyCharm进行第三方开源包安装 前言 如果您觉得有用的话,记得给博主点个赞,评论,收藏一键三连啊,写作不易啊^ _ ^。 而且听说点赞的人每…...
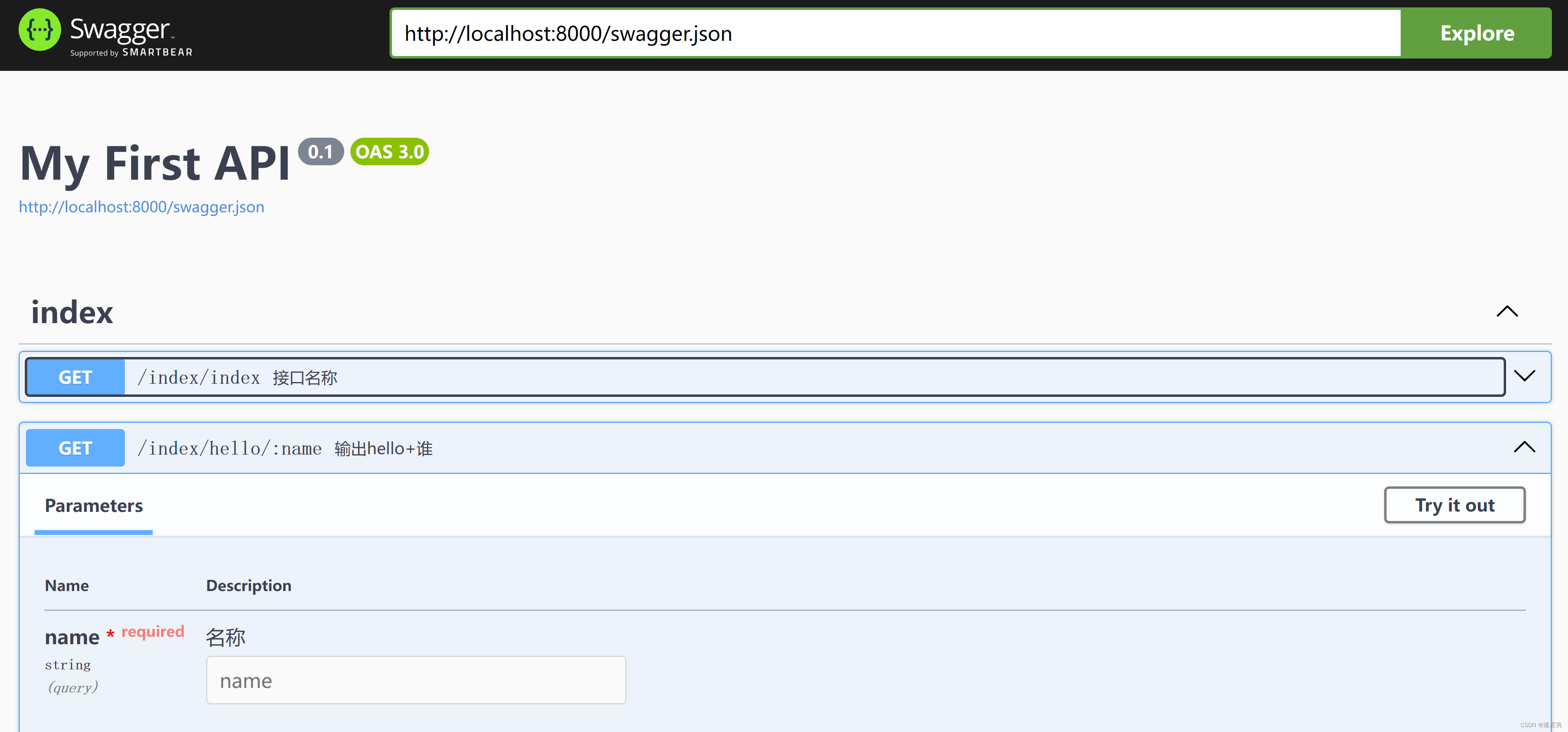
tp6 + swagger 配置文档接口
ThinkPHP 6.0 运行环境要求PHP7.2,兼容PHP8.1 安装 composer create-project topthink/think tp 6.0.*如果需要更新框架使用 composer update topthink/framework文档 完全开发手册 swagger 文档 注解文档 安装包 composer require zircote/swagger-php 引用…...
试图一文彻底讲清 “精准测试”
在软件测试中,我们常常碰到两个基本问题(困难): 很难保障无漏测:我们做了大量测试,但不清楚测得怎样,对软件上线后会不会出问题,没有信心; 选择待执行的测试用例&#…...
Visual Studio 删除行尾空格
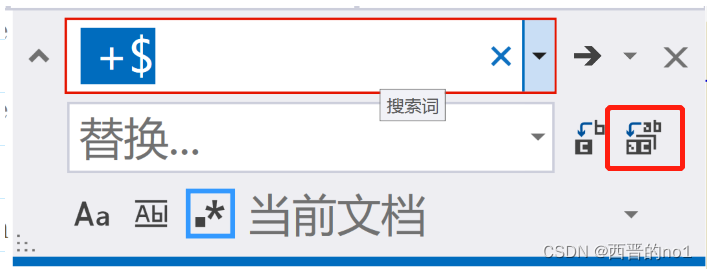
1.CtrlH 打开替换窗口(注意选择合适的查找范围) VS2010: VS2017、VS2022: 2.复制下面正则表达式到上面的选择窗口(注意前面有一个空格): VS2010: $ VS2017、VS2022: $ 3.下面的替换窗口不写入 VS2010: VS2017、VS2022: 4.点选“正则表达式…...

LeetCode_BFS_中等_1926.迷宫中离入口最近的出口
目录 1.题目2.思路3.代码实现(Java) 1.题目 给你一个 m x n 的迷宫矩阵 maze (下标从 0 开始),矩阵中有空格子(用 ‘.’ 表示)和墙(用 ‘’ 表示)。同时给你迷宫的入口 …...

开源Windows12网页版HTML源码
开源Windows12网页版HTML源码,无需安装就能用的Win12网页版来了Windows12概念版(PoweredbyPowerPoint)后深受启发,于是通过使用HTML、CSS、js等技术做了这样一个模拟板的Windows12系统,并已发布至github进行开源。 这…...

vscode中使用指定路径下的cmake
在 Visual Studio Code 中指定自定义的 CMake 路径,你可以通过以下步骤来实现: 打开你的 CMake 项目所在的文件夹,在 Visual Studio Code 中。 在项目文件夹中,创建一个名为 .vscode 的文件夹,如果它还不存在。 在 .…...
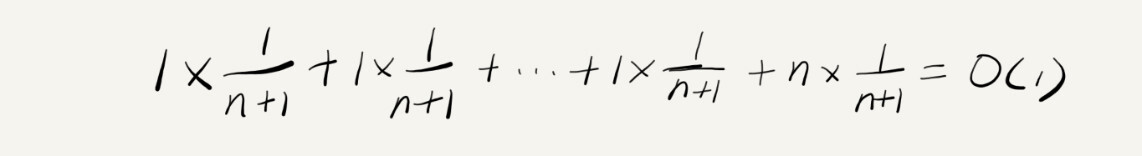
复杂度分析
文章目录 如何分析、统计算法的执行效率和资源消耗?为什么需要复杂度分析?测试结果非常依赖测试环境测试结果受数据规模的影响很大 大O复杂度表示法时间复杂度分析只关注循环次数最多的一段代码加法法则:总复杂度等于量级最大的那段代码的复杂…...

Linux安装jrockit-jdk1.6.0_29-R28.2.0-4.1.0-linux-x64
下载软件:jrockit-jdk1.6.0_29-R28.2.0-4.1.0-linux-x64.bin 执行安装 ./jrockit-jdk1.6.0_29-R28.2.0-4.1.0-linux-x64.bin 安装提示,一路next,注意第二步修改安装的路径,请修改成: <------------------------ O…...

7.2 怎样定义函数
7.2.1 为什么要定义函数 主要内容: 为什么要定义函数 C语言要求所有在程序中用到的函数必须“先定义,后使用”。这是因为在调用一个函数之前,编译系统需要知道这个函数的名字、返回值类型、功能以及参数的个数与类型。如果没有事先定义&…...

Chrome扩展V2到V3的变化
Chrome扩展manifest V3变化、升级迁移指南_chrome_ZK645945-华为云开发者联盟 (csdn.net) 1.background //V2 "background": "background.js"//V3 "background": {"service_worker": "background.js"} 2.executeScript …...

lock、tryLock、lockInterruptibly有什么区别?
lock、tryLock 和 lockInterruptibly 都是用于线程同步的方法,但它们有不同的行为和用途: lock() 方法:lock() 方法是 Java 中 Lock 接口定义的一部分,它用于获取锁并阻塞当前线程,直到锁可用为止。如果锁当前被其他线程占用,lock() 方法会导致当前线程阻塞,直到锁被释放…...

mysql面试题5:索引、主键、唯一索引、联合索引的区别?什么情况下设置了索引但无法使用?并且举例说明
该文章专注于面试,面试只要回答关键点即可,不需要对框架有非常深入的回答,如果你想应付面试,是足够了,抓住关键点 面试官:说一说索引、主键、唯一索引、联合索引的区别? 索引、主键、唯一索引和联合索引是数据库中常用的索引类型,它们有以下区别: 索引:索引是一种数…...
数据集笔记:纽约花旗共享单车od数据
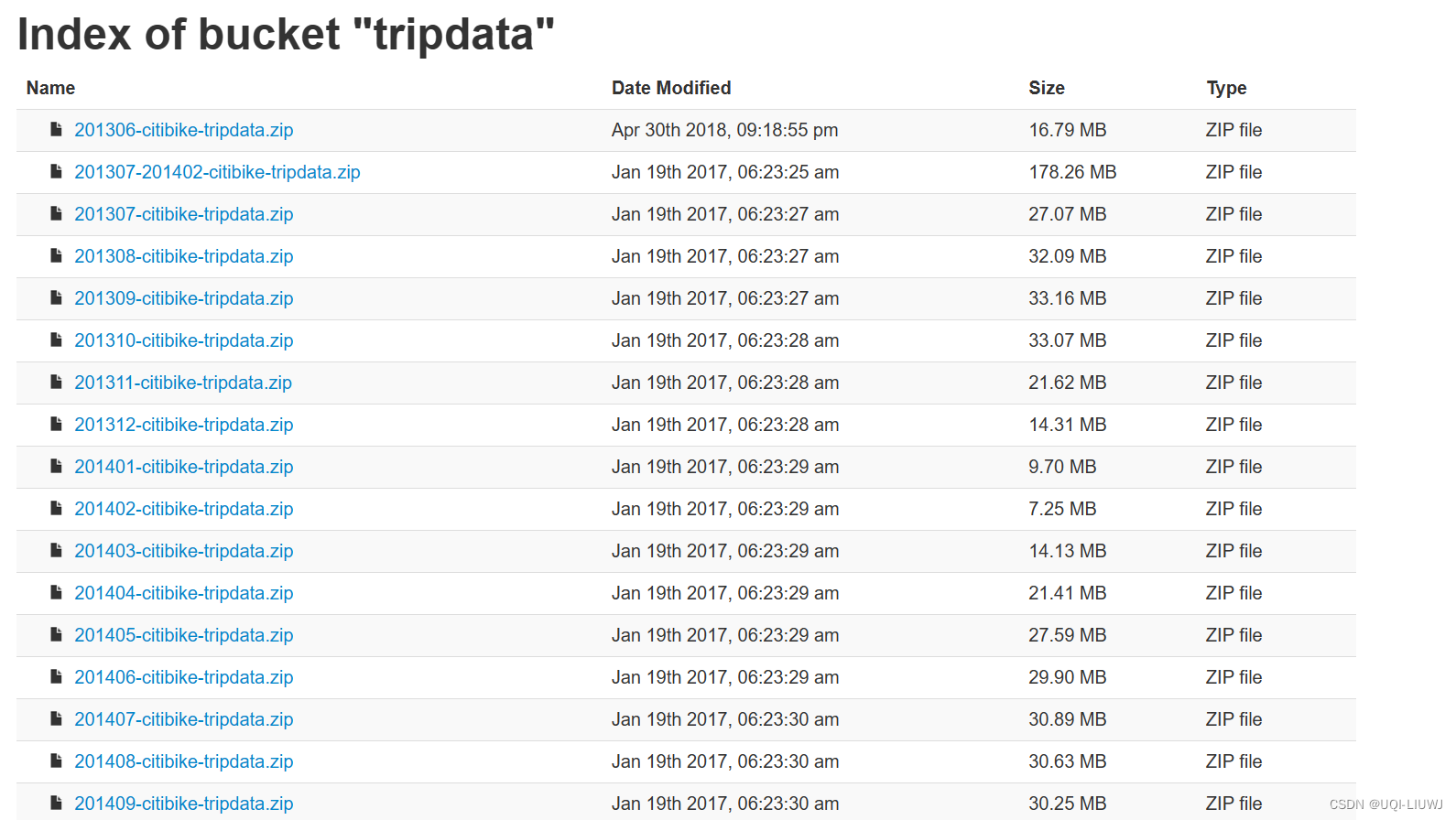
花旗共享单车公布的其共享单车轨迹数据,包括2013年-2021年曼哈顿、布鲁克林、皇后区和泽西城大约14500辆自行车和950个站点的共享单车轨迹数据 数据地址:Citi Bike System Data | Citi Bike NYC | Citi Bike NYC 性别(0未知;1男&…...

为什么 0.1+0.2 不等于 0.3
为什么 0.10.2 不等于 0.3 在 JavaScript 中,0.1 0.2 的结果不等于 0.3,这是因为在 JavaScript 中采用的是双精度浮点数格式(64 位),而在这种格式下无法精确表示某些小数,因此在进行计算时会出现精度误差。…...

huggingface_hub v0.17 现已发布
InferenceClient 现在支持所有任务!💥,感谢社区的巨大努力,新添加的任务包括: 对象检测文本分类Token 分类翻译问题回答表格问题回答填充掩码表格分类表格回归文档问题回答视觉问题回答零样本分类 这些方法还支持使用 …...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

作为测试我们应该关注redis哪些方面
1、功能测试 数据结构操作:验证字符串、列表、哈希、集合和有序的基本操作是否正确 持久化:测试aof和aof持久化机制,确保数据在开启后正确恢复。 事务:检查事务的原子性和回滚机制。 发布订阅:确保消息正确传递。 2、性…...
