第 114 场 LeetCode 双周赛题解
A 收集元素的最少操作次数
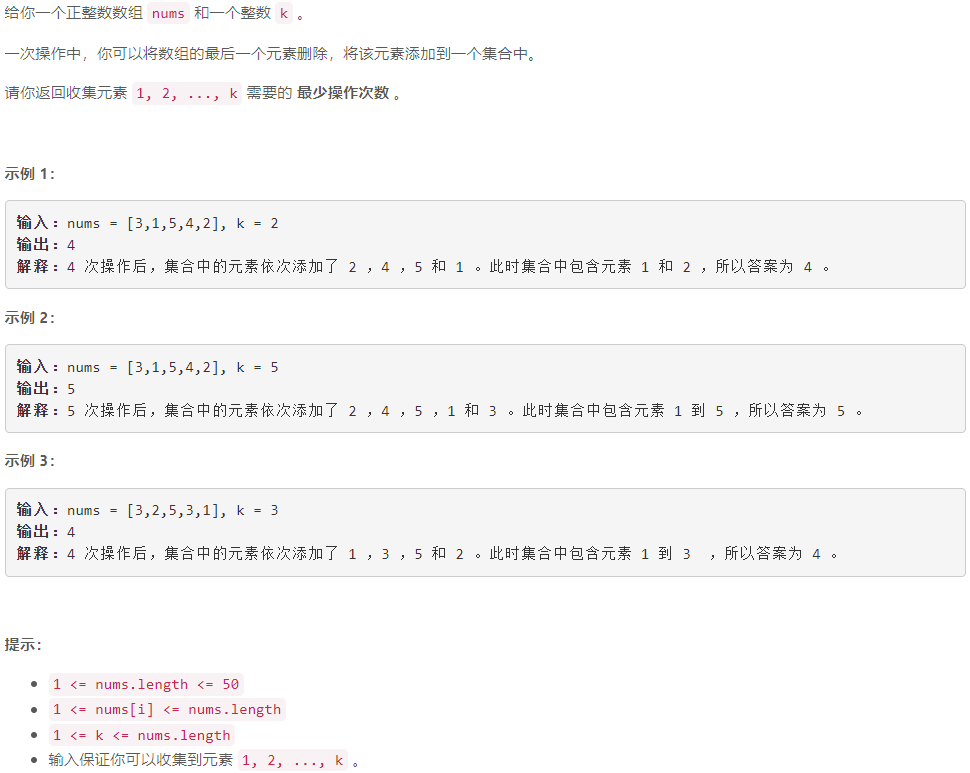
模拟: 反序遍历数组,用一个集合存当前遍历过的不超过 k k k 的正数
class Solution {
public:int minOperations(vector<int> &nums, int k) {unordered_set<int> vis;int n = nums.size();int i = n - 1;for (;; i--) {if (nums[i] <= k && !vis.count(nums[i]))vis.insert(nums[i]);if (vis.size() == k)break;}return n - i;}
};
B 使数组为空的最少操作次数
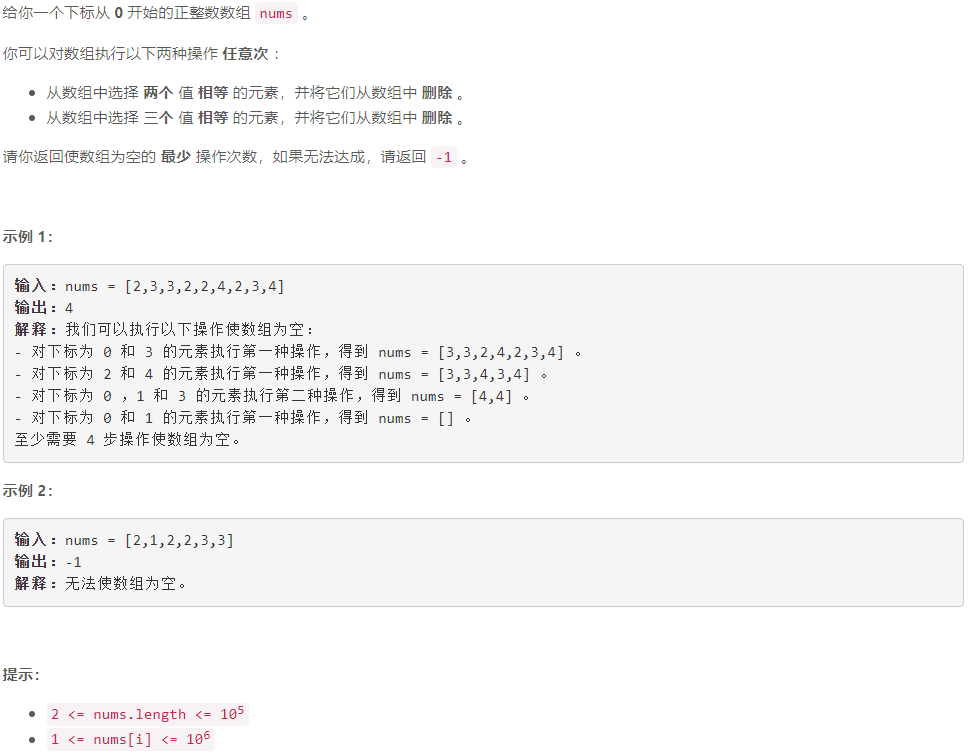
计数:记录数组中各元素出现次数,若存在只出现一次的元素则无法使数组为空,否则,要将出现次数为 f f f 的某个元素全部删除最少需要的次数为:当 f % 3 = 0 f\%3=0 f%3=0 时为 f 3 \frac f 3 3f ,当 f % 3 ≠ 0 f\%3\ne 0 f%3=0 时为 ⌊ f 3 ⌋ + 1 \left \lfloor \frac f 3 \right \rfloor + 1 ⌊3f⌋+1 。
class Solution {
public:int minOperations(vector<int> &nums) {unordered_map<int, int> cnt;for (auto x: nums)cnt[x]++;int res = 0;for (auto [_, f]: cnt) {if (f == 1)return -1;if (f % 3 == 0)res += f / 3;elseres += f / 3 + 1;}return res;}
};
C 将数组分割成最多数目的子数组
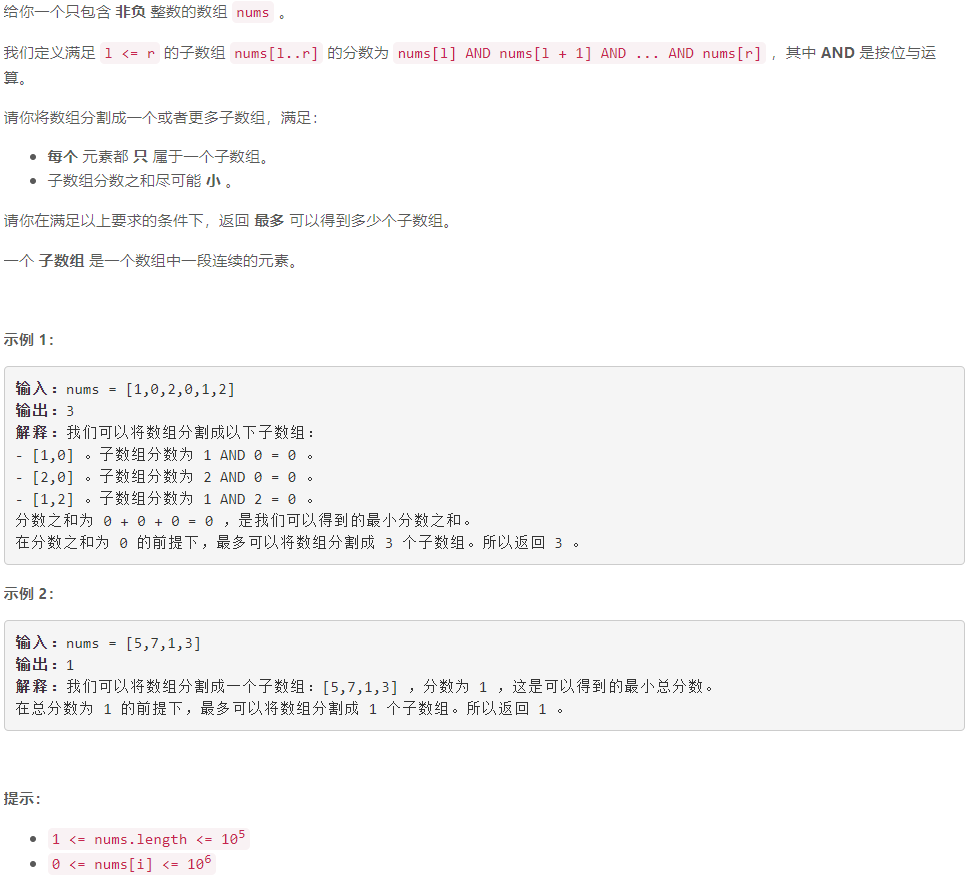
模拟:遍历数组元素 n u m s [ i ] nums[i] nums[i] ,若 n u m s [ i ] nums[i] nums[i] 不是最后一个元素,则只有一种情况会使得最优解中 n u m s [ i ] nums[i] nums[i] 为其所在子数组的最后一个元素: n u m s [ i ] nums[i] nums[i] 所在的子数组分数已经为 0 0 0 且 n u m s [ i + 1 ] & ⋯ & n u m s [ n u m s . s i z e ( ) − 1 ] nums[i+1]\&\cdots\&nums[nums.size()-1] nums[i+1]&⋯&nums[nums.size()−1] 等于 0 0 0
class Solution {
public:int maxSubarrays(vector<int> &nums) {int n = nums.size();vector<int> sf(n);//“后缀与”数组sf[n - 1] = nums[n - 1];for (int i = n - 2; i >= 0; i--)sf[i] = nums[i] & sf[i + 1];int res = 0;for (int i = 0, cur = nums[0]; i < n; i++) {cur &= nums[i];if (i == n - 1 || cur == 0 && sf[i + 1] == 0) {//nums[i]为所在子数组的最后一个元素res++;if (i != n - 1)cur = nums[i + 1];//下一个子数组的首个元素}}return res;}
};
D 可以被 K 整除连通块的最大数目
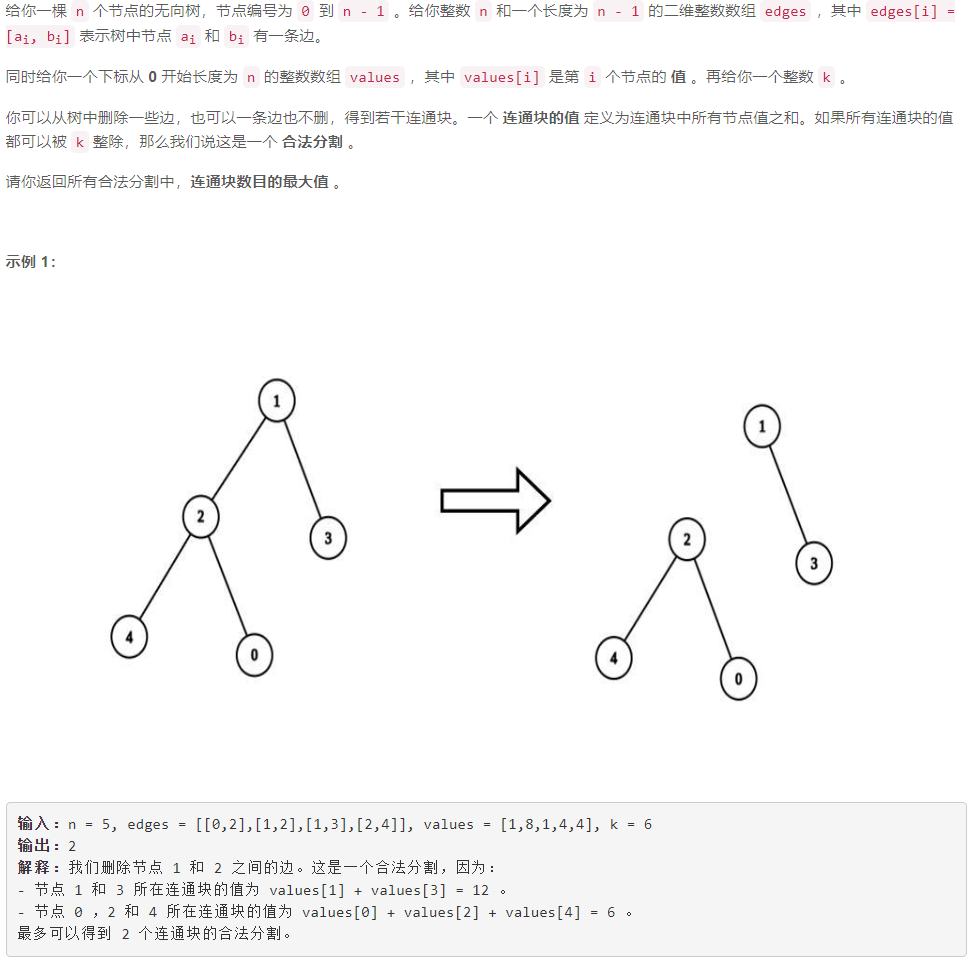
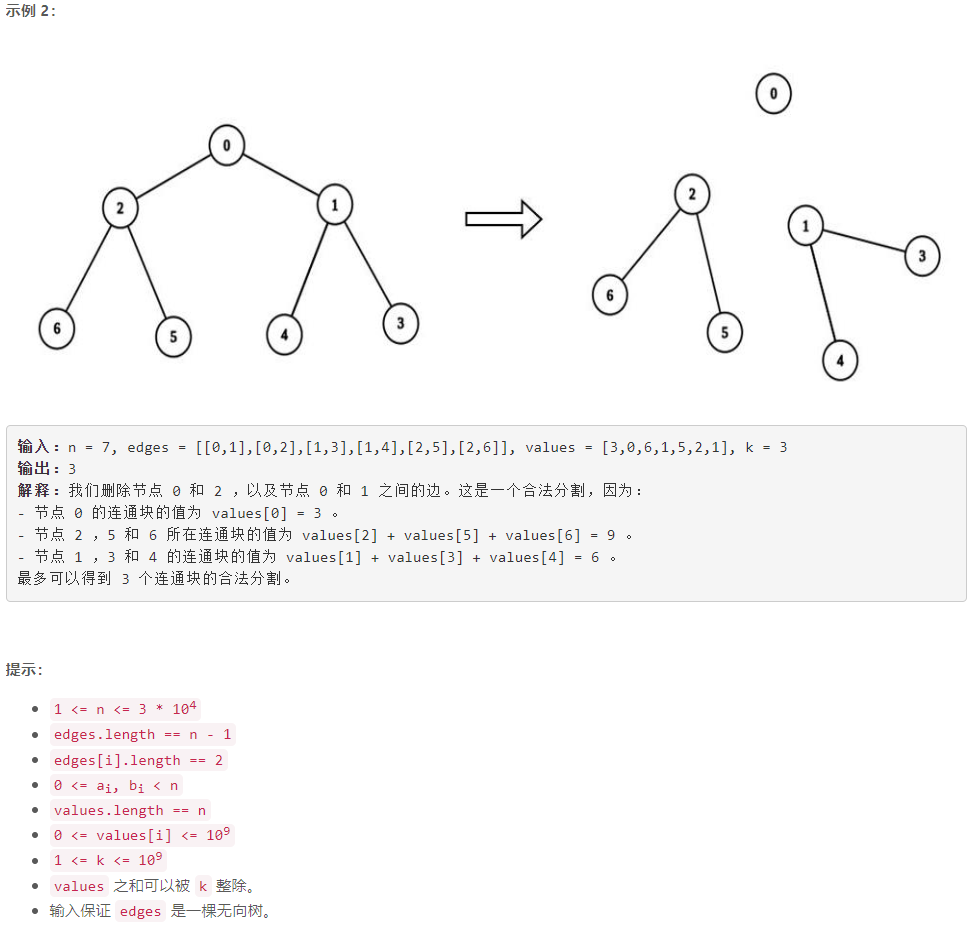
d f s dfs dfs:不妨以 0 0 0 为树根,通过 d f s dfs dfs 求 s s s 数组: s [ i ] s[i] s[i] 为以 i i i 为根的子树的所有节点值之和。设 d f s dfs dfs 遍历到的当前节点为 c u r cur cur ,若遍历到 c u r cur cur 的子节点 j j j 时,有 s [ j ] % k = = 0 s[j]\%k==0 s[j]%k==0 ,则边 ( c u r , j ) (cur,j) (cur,j) 可以删除(即可以增加一个连通块)。
class Solution {
public:using ll = long long;int maxKDivisibleComponents(int n, vector<vector<int>> &edges, vector<int> &values, int k) {vector<int> e[n];//邻接表for (auto &ei: edges) {//建图e[ei[0]].push_back(ei[1]);e[ei[1]].push_back(ei[0]);}vector<ll> s(n);int res = 1;function<ll(int, int)> dfs = [&](int cur, int par) {//当前节点为cur,父节点为pars[cur] += values[cur];for (auto j: e[cur])if (j != par) {s[cur] += dfs(j, cur);if (s[j] % k == 0)res++;}return s[cur];};dfs(0, -1);//以0为根跑dfsreturn res;}
};
相关文章:

第 114 场 LeetCode 双周赛题解
A 收集元素的最少操作次数 模拟: 反序遍历数组,用一个集合存当前遍历过的不超过 k k k 的正数 class Solution { public:int minOperations(vector<int> &nums, int k) {unordered_set<int> vis;int n nums.size();int i n - 1;for (;; i--) {if…...

[Java框架] Java常用爬虫框架推荐
Selenium GitHub 截止 2023年9月份 Star数量27.7K Selenium是一款基于浏览器自动化的工具,它可以模拟用户在浏览器上的操作行为,并获取网页上的内容。Selenium支持多种浏览器,可以很好地处理JavaScript生成内容。但是Selenium相较于其他框架而…...
Kafka:安装与简单使用
文章目录 下载安装windows安装目录结构启动服务器创建主题发送一些消息启动消费者设置多代理集群常见问题 工具kafka tool 常用指令topic查看topic删除topic 常见问题参考文献 下载安装 下载地址:kafka-download windows安装 下载完后,找一个目录解压…...
029-从零搭建微服务-消息队列(一)
写在最前 如果这个项目让你有所收获,记得 Star 关注哦,这对我是非常不错的鼓励与支持。 源码地址(后端):mingyue: 🎉 基于 Spring Boot、Spring Cloud & Alibaba 的分布式微服务架构基础服务中心 源…...

Python2020年06月Python二级 -- 编程题解析
题目一 数字转汉字 用户输入一个1~9(包含1和9)之间的任一数字,程序输出对应的汉字。 如输入2,程序输出“二”。可重复查询。 答案: 方法一 list1[一,二,三,四,五,六,七,八,九] while True:n int(input(请输入1~9之间任意一个数字…...
差分放大器的精髓:放大差模信号 抑制共模信号
参考如图基本的差分放大电路,在R1R2 R3R4的条件下,其输出与输入的关系为 : 具体推导过程参考:差分运算放大器的放大倍数的计算及结论_正在黑化的KS的博客-CSDN博客 由这个式子我们可以发现,差分放大器放大的是同相端与…...

蓝桥等考Python组别九级006
第一部分:选择题 1、Python L9 (15分) 运行下面程序,可以输出几行“*”?( ) for i in range(6): for j in range(7): print(*, end ) print() 5678 正确答案:B 2、Python …...

初级篇—第五章子查询
文章目录 什么是子查询需求分析与问题解决子查询的基本语法结构子查询的分类 单行子查询单行比较操作符代码示例HAVING 中的子查询CASE中的子查询子查询中的空值问题非法使用子查询 多行子查询多行比较操作符代码示例空值问题 相关子查询代码示例在ORDER BY 中使用子查询EXISTS…...
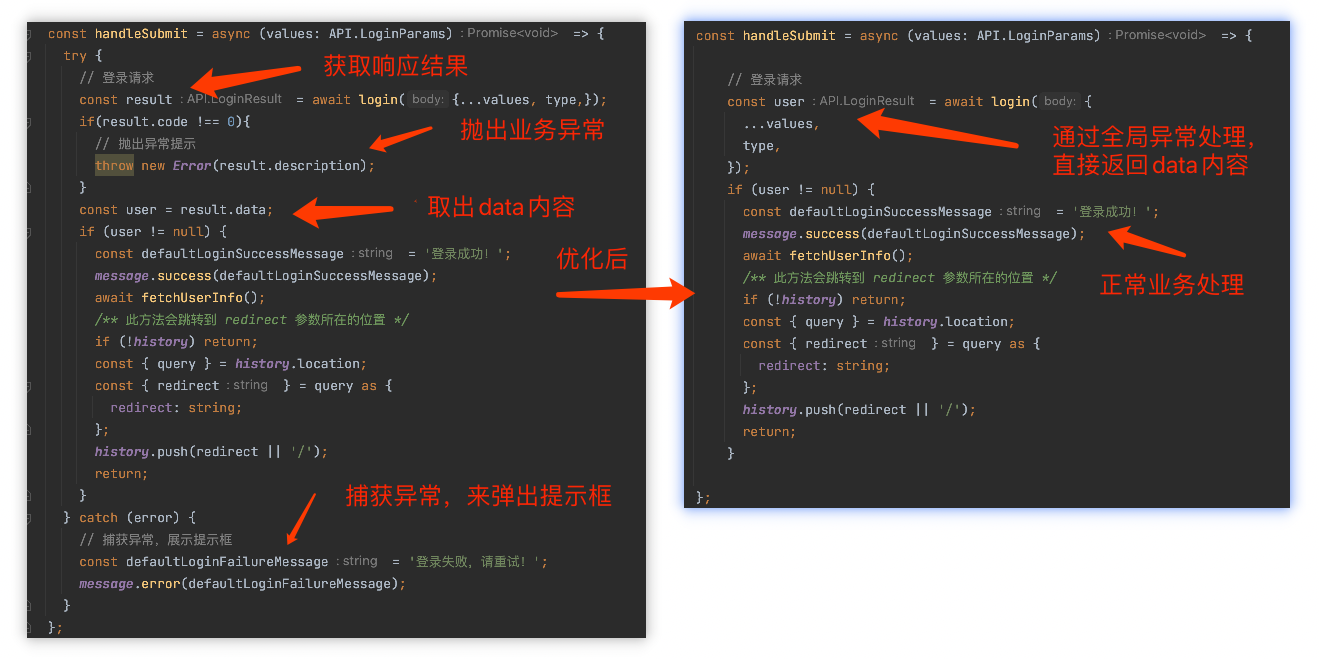
【AntDesign】封装全局异常处理-全局拦截器
[toc] 场景 本文前端用的是阿里的Ant-Design框架,其他框架也有全局拦截器,思路是相同,具体实现自行百度下吧 因为每次都需要调接口,都需要单独处理异常情况(code !0),因此前端需要对后端返回的…...

Visual Studio 代码显示空格等空白符
1.VS2010: 快捷键:CtrlR,W 2.VS2017、VS2019、VS2022: 工具 -> 选项 -> 文本编辑器 -> 显示 -> 勾选查看空白...
紫光同创FPGA图像视频采集系统,基于OV7725实现,提供工程源码和技术支持
目录 1、前言免责声明 2、设计思路框架视频源选择OV7725摄像头配置及采集动态彩条HDMA图像缓存输入输出视频HDMA缓冲FIFOHDMA控制模块HDMI输出 3、PDS工程详解4、上板调试验证并演示准备工作静态演示动态演示 5、福利:工程源码获取 紫光同创FPGA图像视频采集系统&am…...
京东大型API网关实践之路
概述 1、背景 京东作为电商平台,近几年用户、业务持续增长,访问量持续上升,随着这些业务的发展,API网关应运而生。 API网关,就是为了解放客户端与服务端而存在的。对于客户端,使开放给客户端的接口标准统…...

图像处理: 马赛克艺术
马赛克 第一章 马赛克的历史渊源 1.1 马赛克 艺术中的一种表面装饰,由紧密排列的、通常颜色各异的小块材料(如石头、矿物、玻璃、瓷砖或贝壳)组成。与镶嵌不同的是,镶嵌是将要应用的部件放置在已挖空以容纳设计的表面中࿰…...
postgresql-管理数据表
postgresql-管理数据表 创建表数据类型字段约束表级约束模式搜索路径 修改表添加字段删除字段添加约束删除约束修改字段默认值修改字段数据类型重命名字段重命名表 删除表 创建表 在 PostgreSQL 中,使用 CREATE TABLE 语句创建一个新表: CREATE TABLE …...
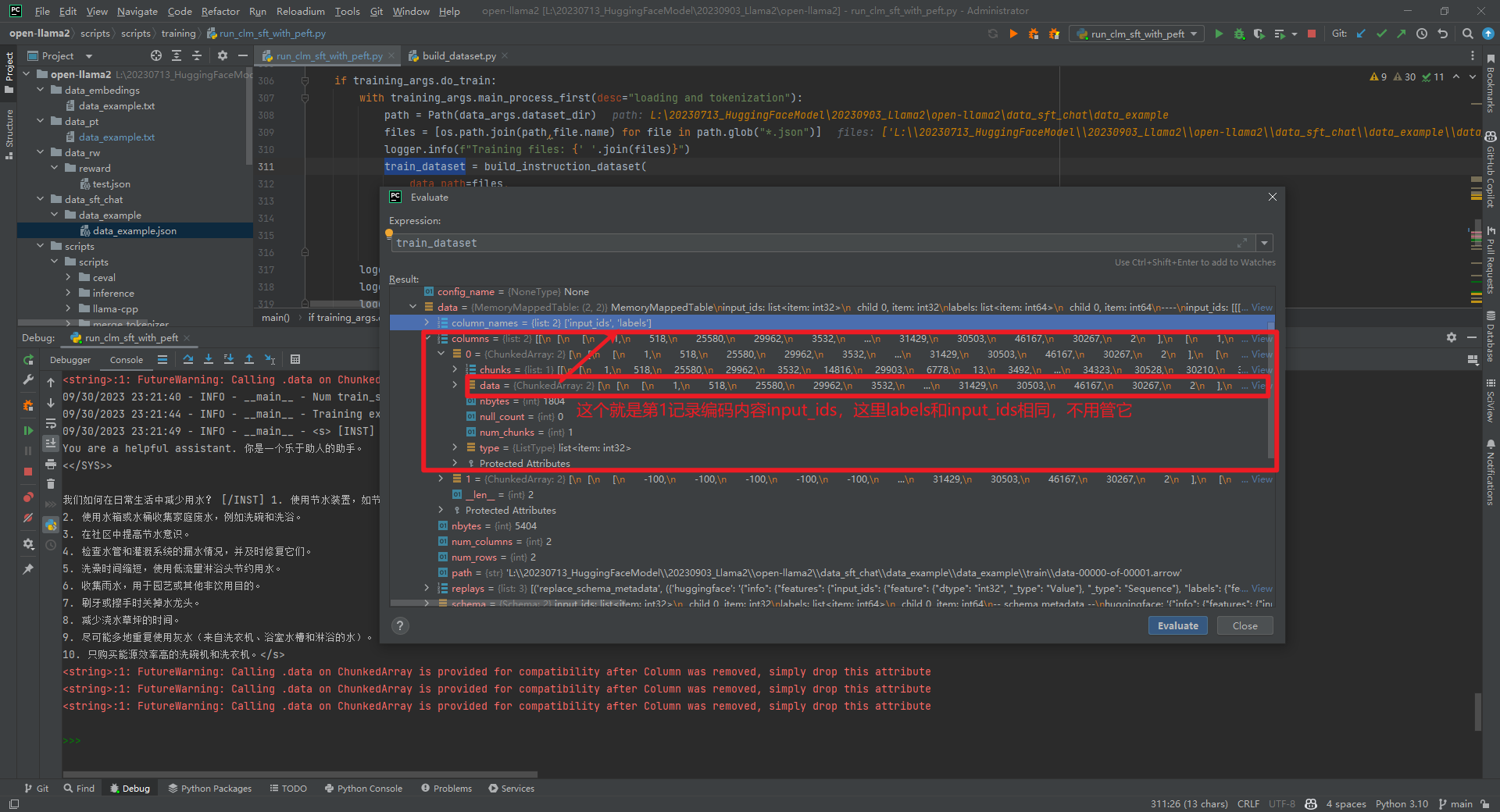
Llama2-Chinese项目:3.1-全量参数微调
提供LoRA微调和全量参数微调代码,训练数据为data/train_sft.csv,验证数据为data/dev_sft.csv,数据格式如下所示: "<s>Human: "问题"\n</s><s>Assistant: "答案举个例子,如下所…...

蓝桥等考Python组别十级001
第一部分:选择题 1、Python L10 (15分) 已知s = Hello!,下列说法正确的是( )。 s[1]对应的字符是Hs[2]对应的字符是ls[-1]对应的字符是os[3]对应的字符是o正确答案:B 2、Python L10 (15分) 运行下面程序,输入字符串“Banana”,输出的结果是&#x...

记录 Git 操作时遇到的问题及解决方案
目录 问题:git pull 时报错报错内容: ! [rejected] v1.0.3 -> v1.0.3 (would clobber existing tag)原因:本地 Git 仓库中已经存在名为 v1.0.3 和 v1.0.6 的标签了,而尝试从远程仓库(GitHub)拉取这些标签…...
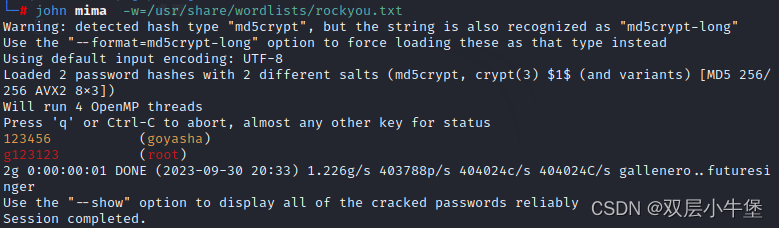
第一届“龙信杯”电子数据取证竞赛Writeup
目录 移动终端取证 请分析涉案手机的设备标识是_______。(标准格式:12345678) 请确认嫌疑人首次安装目标APP的安装时间是______。(标准格式:2023-09-13.11:32:23) 此检材共连接过______个WiFi。&#x…...

Vue与React//双绑问题
Vue和React是两个目前最流行的前端框架,它们有一些区别主要区别如下: 响应式原理:Vue使用基于模板的方式进行双向绑定,其中使用了Vue自己实现的响应式系统。Vue能够通过追踪数据的依赖关系,自动更新DOM元素。而React采…...

信息安全第四周
社会工程学 社会工程学主要研究如何操纵人的心理和情感来获取机密信息或其他目标。它主要不是通过技术手段攻击计算机系统,而是通过心理学和人际交往技巧来欺骗人,使他们泄露密码、安全代码或其他敏感信息。社会工程学主要是一种安全风险,主要…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...
