怒刷LeetCode的第21天(Java版)
目录
第一题
题目来源
题目内容
解决方法
方法一:哈希表
方法二:计数器数组
第二题
题目来源
题目内容
解决方法
方法一:分治法
方法二:快速幂 + 迭代
方法三:快速幂 + 递归
第三题
题目来源
题目内容
解决方法
方法一:回溯算法
方法二:基于集合的回溯
方法三:基于位运算的回溯
方法四:DFS(深度优先搜索)
第一题
题目来源
49. 字母异位词分组 - 力扣(LeetCode)
题目内容

解决方法
方法一:哈希表
思路: 首先,我们可以使用哈希表来存储字母异位词分组的结果。遍历字符串数组中的每个字符串,对每个字符串进行排序,得到其排序后的字符串作为哈希表的键。然后将原始字符串添加到对应键的列表中,最后返回哈希表的值即可。
import java.util.*;
class Solution {public List<List<String>> groupAnagrams(String[] strs) {// 创建一个哈希表,key 为排序后的字符串,value 为相同排序后字符串的原始字符串列表Map<String, List<String>> map = new HashMap<>();// 遍历字符串数组for (String str : strs) {// 将字符串转为字符数组并排序char[] arr = str.toCharArray();Arrays.sort(arr);String sortedStr = String.valueOf(arr);// 如果哈希表中不存在该键,则新建一个键值对if (!map.containsKey(sortedStr)) {map.put(sortedStr, new ArrayList<>());}// 将原始字符串添加到对应键的列表中map.get(sortedStr).add(str);}// 返回哈希表的值,即分组后的结果列表return new ArrayList<>(map.values());}
}
复杂度分析:
时间复杂度分析:
- 对于每个字符串,需要将其排序,排序的时间复杂度为 O(klogk),其中 k 为字符串的长度。
- 总共有 n 个字符串,因此总时间复杂度为 O(nklogk)。
空间复杂度分析:
- 使用了一个哈希表来存储分组的结果,最多包含 n 个键值对。
- 每个键值对中的值是一个列表,列表的最大长度为 n。
- 因此,空间复杂度为 O(n)。
综上所述,该解法的时间复杂度为 O(nklogk),空间复杂度为 O(n)。
LeetCode运行结果:
方法二:计数器数组
除了使用哈希表的方法,我们还可以通过使用计数器数组来实现字母异位词的分组。
具体思路如下:
- 创建一个长度为26的整型数组count,用于记录每个字母出现的次数。
- 遍历字符串数组中的每个字符串:
- 将count数组每个位置的值都置为0,用于统计当前字符串的字符出现次数。
- 遍历当前字符串,将每个字符出现的次数加到count数组对应的位置上。
- 将count数组转换为一个唯一的字符串作为哈希表的键。
- 将当前字符串添加到对应键的列表中。
- 返回哈希表的值,即分组后的结果列表。
import java.util.*;class Solution {public List<List<String>> groupAnagrams(String[] strs) {// 创建一个哈希表,key 为唯一的计数器字符串,value 为相同计数器字符串的原始字符串列表Map<String, List<String>> map = new HashMap<>();// 遍历字符串数组for (String str : strs) {// 创建一个长度为26的计数器数组int[] count = new int[26];// 统计当前字符串中每个字符出现的次数for (char c : str.toCharArray()) {count[c - 'a']++;}// 将计数器数组转换为一个唯一的字符串作为哈希表的键StringBuilder sb = new StringBuilder();for (int i = 0; i < 26; i++) {sb.append('#');sb.append(count[i]);}String key = sb.toString();// 如果哈希表中不存在该键,则新建一个键值对if (!map.containsKey(key)) {map.put(key, new ArrayList<>());}// 将原始字符串添加到对应键的列表中map.get(key).add(str);}// 返回哈希表的值,即分组后的结果列表return new ArrayList<>(map.values());}
}
复杂度分析:
时间复杂度分析:
- 对于每个字符串,需要遍历一次,并统计字符出现的次数,时间复杂度为 O(k)。
- 总共有 n 个字符串,因此总时间复杂度为 O(nk)。
空间复杂度分析:
- 使用了一个哈希表来存储分组的结果,最多包含 n 个键值对。
- 每个键值对中的值是一个列表,列表的最大长度为 n。
- 因此,空间复杂度为 O(n)。
综上所述,该解法的时间复杂度为 O(nk),空间复杂度为 O(n)。
LeetCode运行结果:
第二题
题目来源
50. Pow(x, n) - 力扣(LeetCode)
题目内容
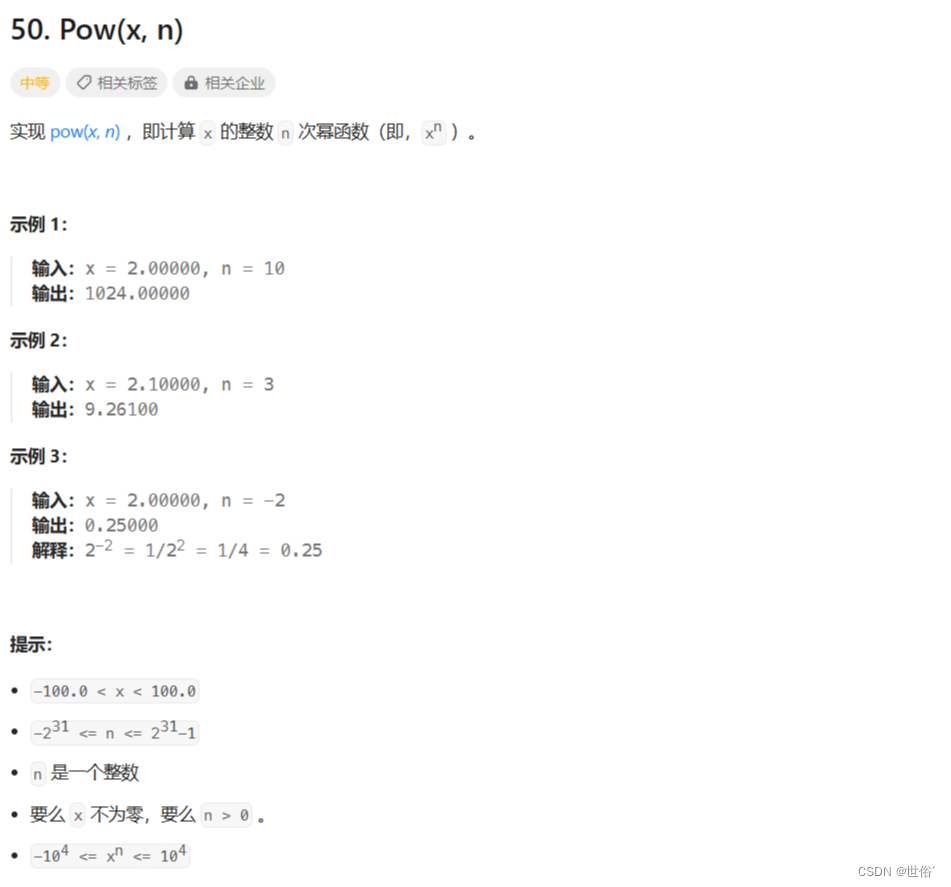
解决方法
方法一:分治法
根据题目要求,可以使用分治法来实现 pow(x, n) 函数。具体做法如下:
- 若 n < 0,则转换为求解 pow(1/x, -n)。
- 定义递归函数 helper(x, n),表示计算 x 的整数 n 次幂。
- 当 n 为 0 时,返回 1。
- 当 n 为偶数时,将问题规模缩小一半,即计算 helper(x, n/2) * helper(x, n/2)。
- 当 n 为奇数时,将结果乘以 x,即计算 x * helper(x, n/2) * helper(x, n/2)。
- 根据 n 的正负性,返回最终结果。
public class Solution {public double myPow(double x, int n) {// 若指数 n 为负数,则转换为求解 pow(1/x, -n)if (n < 0) {x = 1 / x;n = -n;}return helper(x, n);}private double helper(double x, int n) {// 递归结束条件:n 为 0if (n == 0) {return 1.0;}// 递归计算一半的结果double half = helper(x, n / 2);// 若 n 为偶数if (n % 2 == 0) {return half * half;}// 若 n 为奇数else {return x * half * half;}}
}
复杂度分析:
时间复杂度分析:
- 每次递归,问题规模缩小一半,因此递归的层数为 O(logn)。
- 在每一层递归中,需要进行一次乘法运算。因此,总时间复杂度为 O(logn)。
空间复杂度分析:
- 使用了 O(logn) 的递归栈空间。
LeetCode运行结果:
方法二:快速幂 + 迭代
算法思路: 首先,将指数 n 转化为 long 类型的 N,以处理负数指数的情况。 然后,对于任意一个实数 x 和非负整数 N,可以通过二分法迭代计算出 x^N 的值。
假设已经计算出 x^{N/2},那么有以下两种情况:
当 N 为偶数时,有:x^N = (x^{N/2})^2 当 N 为奇数时,有:x^N = x * (x^{N/2})^2
通过上面两种情况,可以将原问题分解成规模更小的子问题,并且每次只需进行一次乘法运算即可。不断重复这个过程,最终可以得到 x^N 的值。
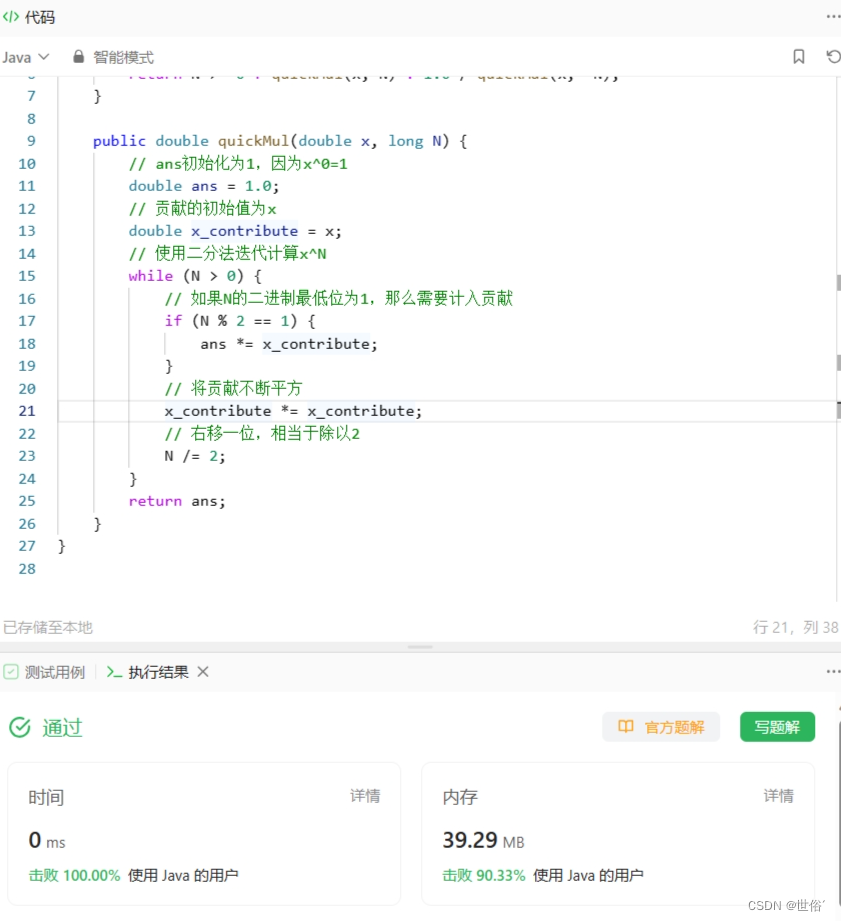
class Solution {public double myPow(double x, int n) {// 将指数转化为long类型的N,以处理负数指数的情况long N = n;// 如果N为负数,将x变为1/x,指数变为相反数return N >= 0 ? quickMul(x, N) : 1.0 / quickMul(x, -N);}public double quickMul(double x, long N) {// ans初始化为1,因为x^0=1double ans = 1.0;// 贡献的初始值为xdouble x_contribute = x;// 使用二分法迭代计算x^Nwhile (N > 0) {// 如果N的二进制最低位为1,那么需要计入贡献if (N % 2 == 1) {ans *= x_contribute;}// 将贡献不断平方x_contribute *= x_contribute;// 右移一位,相当于除以2N /= 2;}return ans;}
}
复杂度分析:
- 时间复杂度:由于每次将指数减半,因此算法的迭代次数为 logn。每次迭代只需要进行一次乘法运算,因此总时间复杂度为 O(logn)。
- 空间复杂度:算法中只使用了常数个变量,因此空间复杂度为 O(1)。
LeetCode运行结果:
方法三:快速幂 + 递归
算法思路: 假设已经计算出 x^{N/2},那么有以下两种情况:
当 N 为偶数时,有:x^N = (x^{N/2})^2 当 N 为奇数时,有:x^N = x * (x^{N/2})^2
通过上面两种情况,可以将原问题分解成规模更小的子问题,并且每次只需进行一次乘法运算即可。不断重复这个过程,最终可以得到 x^N 的值。
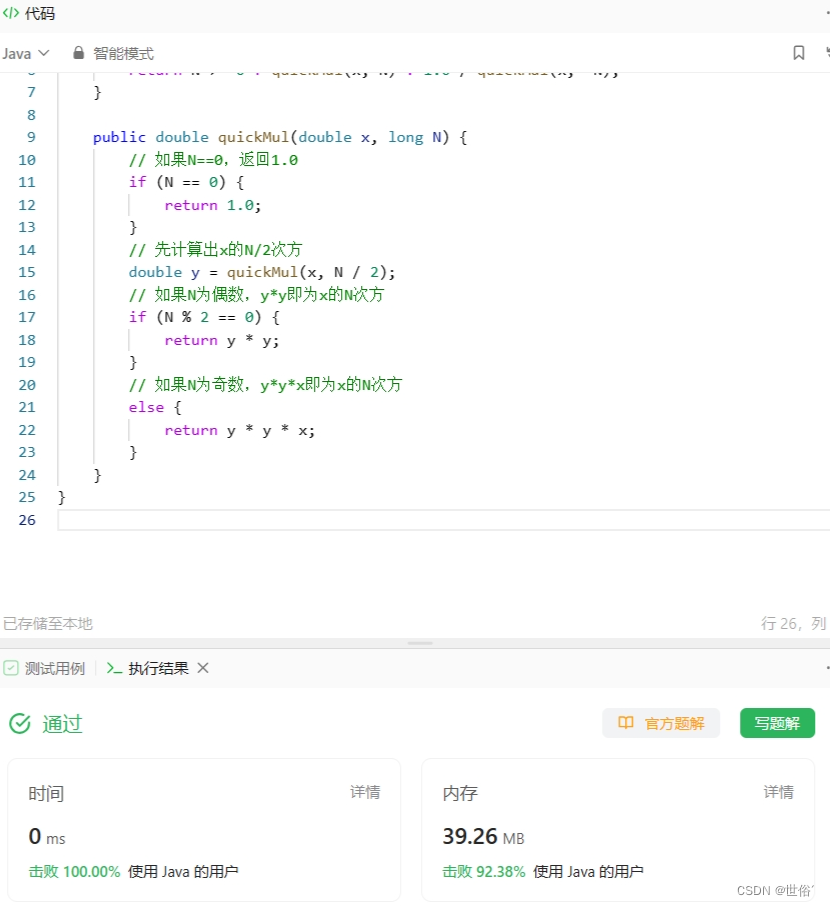
class Solution {public double myPow(double x, int n) {// 将指数转化为long类型的N,以处理负数指数的情况long N = n;// 如果N为负数,将x变为1/x,指数变为相反数return N >= 0 ? quickMul(x, N) : 1.0 / quickMul(x, -N);}public double quickMul(double x, long N) {// 如果N==0,返回1.0if (N == 0) {return 1.0;}// 先计算出x的N/2次方double y = quickMul(x, N / 2);// 如果N为偶数,y*y即为x的N次方if (N % 2 == 0) {return y * y;}// 如果N为奇数,y*y*x即为x的N次方else {return y * y * x;}}
}
复杂度分析:
- 时间复杂度:由于每次将指数减半,因此算法的迭代次数为 logn。每次迭代只需要进行一次乘法运算,因此总时间复杂度为 O(logn)。
- 空间复杂度:由于算法使用了递归来实现快速幂运算,因此最坏情况下递归的深度为 logn,因此空间复杂度为 O(logn)。
LeetCode运行结果:
第三题
题目来源
51. N 皇后 - 力扣(LeetCode)
题目内容

解决方法
方法一:回溯算法
N 皇后问题可以使用回溯算法来求解。回溯算法是一种深度优先搜索的算法,通过递归地尝试所有可能的解决方案,并在不满足条件时进行回溯。
具体思路如下:
- 创建一个长度为
n的数组queens,用于存储每一行皇后所在的列索引。初始化时,所有元素都为-1,表示还没有放置皇后。 - 使用回溯函数进行递归搜索,函数定义如下:
- 参数
row表示当前正在放置皇后的行数。 - 参数
n表示棋盘的大小,也表示需要放置的皇后的数量。 - 在递归的过程中,从左到右依次尝试放置皇后,对于每个位置
(row, col),判断是否可以放置皇后的条件是不在同一列或同一斜线上。如果可以放置,则将queens[row]设置为col,表示在当前行放置皇后的位置为(row, col)。 - 如果当前行是最后一行(即
row == n - 1),说明找到了一种解法,将该解法存储起来。 - 如果当前行不是最后一行,则继续递归放置下一行的皇后。
- 在递归结束后,需要进行回溯操作,即撤销当前行放置的皇后,尝试放置下一个位置。
- 参数
- 创建一个函数
isValid(row, col, n)来判断当前位置是否可以放置皇后。判断的条件是不在同一列或同一斜线上。具体判断方法如下:- 对于每一行,使用数组
queens存储了已经放置的皇后位置,因此只需要判断列号是否相等或者斜率是否为 ±1±1 即可。
- 对于每一行,使用数组
- 最后,将所有解法转换为字符串表示,存储到结果列表中,并返回作为结果。
class Solution {// 存储每一行皇后所在的列索引int[] queens;// 存储所有解法List<List<String>> solutions;public List<List<String>> solveNQueens(int n) {queens = new int[n];solutions = new ArrayList<>();backtrack(0, n);return solutions;}// 回溯函数private void backtrack(int row, int n) {if (row == n) { // 找到一种解法List<String> solution = generateSolution(n);solutions.add(solution);} else {for (int col = 0; col < n; col++) {if (isValid(row, col, n)) { // 判断当前位置是否可以放置皇后queens[row] = col;backtrack(row + 1, n); // 继续下一行的回溯}}}}// 判断当前位置是否可以放置皇后private boolean isValid(int row, int col, int n) {for (int i = 0; i < row; i++) {int diff = Math.abs(col - queens[i]);if (diff == 0 || diff == row - i) { // 判断是否在同一列或同一斜线上return false;}}return true;}// 生成解法的字符串表示private List<String> generateSolution(int n) {List<String> solution = new ArrayList<>();for (int row = 0; row < n; row++) {StringBuilder sb = new StringBuilder();for (int col = 0; col < n; col++) {if (col == queens[row]) {sb.append("Q");} else {sb.append(".");}}solution.add(sb.toString());}return solution;}
}
复杂度分析:
- 时间复杂度:在回溯算法中,对于每一行的每一个位置,都需要进行判断。在判断当前位置是否可以放置皇后时,需要遍历已经放置的皇后,时间复杂度为 O(N)。因此,在放置 N 个皇后的过程中,总体的时间复杂度为 O(N^N \cdot N!),其中 N! 表示 N 的阶乘。
- 空间复杂度:除了存储结果的列表之外,需要额外使用一个数组 queens 来存储每一行皇后所在的列索引,数组的长度为 N。递归调用栈的最大深度为 N。因此,额外的空间复杂度为 O(N)。
需要注意的是,以上复杂度分析是在没有剪枝优化的情况下。实际上,N 皇后问题可以通过剪枝优化来减少搜索的空间和时间复杂度,例如通过判断不同行上皇后的冲突情况,来排除不必要的搜索路径。通过合理的剪枝策略,可以显著提高算法的效率。
总结起来,N 皇后问题的时间复杂度为 O(N^N \cdot N!),空间复杂度为 O(N)。
LeetCode运行结果:

方法二:基于集合的回溯
import java.util.*;
class Solution {
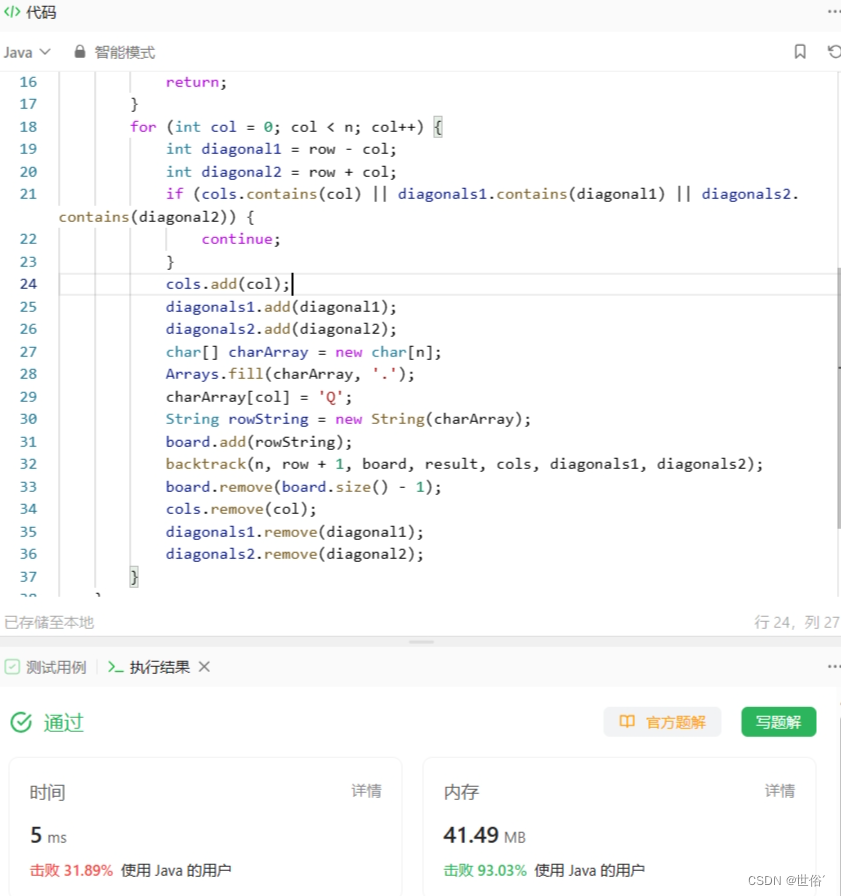
public List<List<String>> solveNQueens(int n) {List<List<String>> result = new ArrayList<>();Set<Integer> cols = new HashSet<>();Set<Integer> diagonals1 = new HashSet<>();Set<Integer> diagonals2 = new HashSet<>();backtrack(n, 0, new ArrayList<>(), result, cols, diagonals1, diagonals2);return result;}private void backtrack(int n, int row, List<String> board, List<List<String>> result,Set<Integer> cols, Set<Integer> diagonals1, Set<Integer> diagonals2) {if (row == n) {result.add(new ArrayList<>(board));return;}for (int col = 0; col < n; col++) {int diagonal1 = row - col;int diagonal2 = row + col;if (cols.contains(col) || diagonals1.contains(diagonal1) || diagonals2.contains(diagonal2)) {continue;}cols.add(col);diagonals1.add(diagonal1);diagonals2.add(diagonal2);char[] charArray = new char[n];Arrays.fill(charArray, '.');charArray[col] = 'Q';String rowString = new String(charArray);board.add(rowString);backtrack(n, row + 1, board, result, cols, diagonals1, diagonals2);board.remove(board.size() - 1);cols.remove(col);diagonals1.remove(diagonal1);diagonals2.remove(diagonal2);}}
}通过回溯的方式,在每一行中的每个位置尝试放置皇后。使用三个集合 cols、diagonals1 和 diagonals2 分别记录已经放置的皇后所在的列、主对角线和副对角线的信息,用于判断是否是合法的放置位置。当放置的皇后数量达到 N 个时,将当前结果加入最终的结果列表中。
注意,在每一次放置皇后之前,需要先判断当前位置是否已经被占据,如果是,则跳过该位置。同时,在回溯的过程中,需要及时撤销之前的操作,即从集合和棋盘中移除皇后的相关信息。
复杂度分析:
N 皇后问题的时间复杂度很难精确地确定,因为不同的搜索方案具有不同的耗时。但是可以确定的是,N 皇后问题解的数量一定是阶乘级别的,即 O(N!)。
在回溯算法中,每次递归处理到第 i 行时,都需要考虑所有列 j 是否可用,因此时间复杂度为 O(N^i)。因此,总的时间复杂度可以表示为: O(N!)
空间复杂度方面,除了存储答案和一些辅助变量外,主要的空间开销是递归调用栈的空间。在最坏情况下,即所有可能的排列方式都需要尝试一遍时,递归栈的深度会达到 N,每层递归需要 O(N) 的空间,因此空间复杂度也是 O(N)。
需要注意的是,在实际应用中,我们可以通过剪枝等方式来优化回溯算法的效率,从而在适当的情况下减小时间和空间的开销。
LeetCode运行结果:
方法三:基于位运算的回溯
当使用位运算来解决 N 皇后问题时,可以通过一个整数的二进制表示来记录每个皇后的位置,其中每个皇后占据一列,皇后所在的行由二进制中的位置表示。
class Solution {
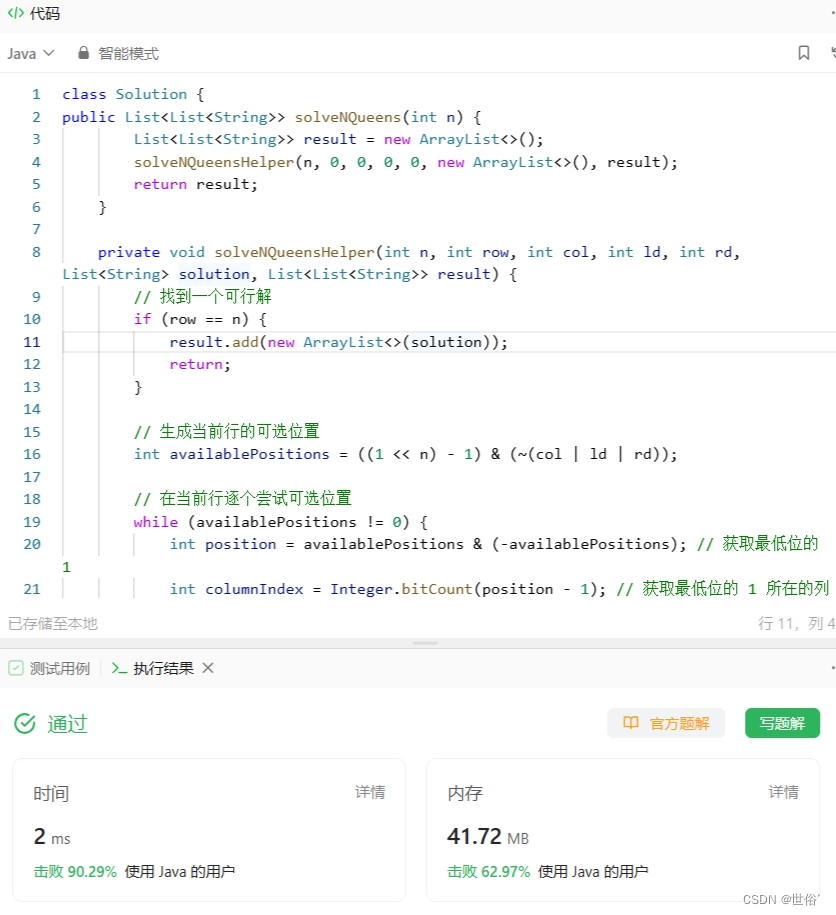
public List<List<String>> solveNQueens(int n) {List<List<String>> result = new ArrayList<>();solveNQueensHelper(n, 0, 0, 0, 0, new ArrayList<>(), result);return result;}private void solveNQueensHelper(int n, int row, int col, int ld, int rd, List<String> solution, List<List<String>> result) {// 找到一个可行解if (row == n) {result.add(new ArrayList<>(solution));return;}// 生成当前行的可选位置int availablePositions = ((1 << n) - 1) & (~(col | ld | rd));// 在当前行逐个尝试可选位置while (availablePositions != 0) {int position = availablePositions & (-availablePositions); // 获取最低位的 1int columnIndex = Integer.bitCount(position - 1); // 获取最低位的 1 所在的列索引// 构建当前行的字符串表示StringBuilder sb = new StringBuilder();for (int i = 0; i < n; i++) {sb.append(i == columnIndex ? 'Q' : '.');}solution.add(sb.toString());// 更新下一行的状态solveNQueensHelper(n, row + 1, col | position, (ld | position) << 1, (rd | position) >> 1, solution, result);// 恢复当前行的状态solution.remove(solution.size() - 1);// 清除最低位的 1,继续尝试下一个可选位置availablePositions &= (availablePositions - 1);}}
}这段代码中,使用位运算来记录每个皇后的位置,其中 col 表示已占据的列,ld 表示已占据的左对角线,rd 表示已占据的右对角线。通过位运算可以快速判断某个位置是否可选。
在 solveNQueensHelper 方法中,递归地尝试每个可选位置,并更新下一行的状态。当找到一个可行解时,将其添加到结果列表中。最后,将整个结果返回。
复杂度分析:
时间复杂度:
- 构建可选位置集合的操作需要遍历每个列,时间复杂度为 O(N)。
- 在递归求解过程中,每行都需要尝试遍历可选位置,时间复杂度为 O(N!)。 综上,总的时间复杂度为 O(N * N!)。
空间复杂度:
- 递归调用栈的深度为 N,每层递归需要常数级别的额外空间,因此空间复杂度为 O(N)。
- 存储结果列表的空间复杂度为 O(N^2 * N!),其中 N^2 是存储每个解所需的空间。 综上,总的空间复杂度为 O(N^2 * N!).
需要注意的是,虽然使用位运算可以提高算法的执行效率,但是在 N 很大时,N 皇后问题仍然是一个非常耗时的问题。因此,在实际应用中,当 N 较大时,可能需要考虑其他更加高效的解决方案。
LeetCode运行结果:
方法四:DFS(深度优先搜索)
import java.util.ArrayList;
import java.util.List;
class Solution {
public List<List<String>> solveNQueens(int n) {List<List<String>> result = new ArrayList<>();boolean[] colUsed = new boolean[n];boolean[] diag1Used = new boolean[2 * n - 1];boolean[] diag2Used = new boolean[2 * n - 1];char[][] board = new char[n][n];for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++) {board[i][j] = '.';}}dfs(0, n, board, colUsed, diag1Used, diag2Used, result);return result;}private void dfs(int row, int n, char[][] board, boolean[] colUsed, boolean[] diag1Used, boolean[] diag2Used, List<List<String>> result) {// 找到一个可行解if (row == n) {List<String> solution = new ArrayList<>();for (int i = 0; i < n; i++) {solution.add(new String(board[i]));}result.add(solution);return;}for (int col = 0; col < n; col++) {int diag1 = row + col;int diag2 = row - col + n - 1;// 检查当前位置是否可放置皇后if (!colUsed[col] && !diag1Used[diag1] && !diag2Used[diag2]) {board[row][col] = 'Q';colUsed[col] = true;diag1Used[diag1] = true;diag2Used[diag2] = true;// 继续搜索下一行dfs(row + 1, n, board, colUsed, diag1Used, diag2Used, result);// 恢复当前位置的状态board[row][col] = '.';colUsed[col] = false;diag1Used[diag1] = false;diag2Used[diag2] = false;}}}
}在这段代码中,我们使用 boolean 数组来表示每一列、每一条正对角线和反对角线是否已经被占用。我们使用二维字符数组来表示棋盘,其中皇后的位置用 'Q' 表示,空位置用 '.' 表示。
在 solveNQueens 方法中,首先初始化棋盘和状态数组,然后调用 dfs 方法进行深度优先搜索。
dfs 方法采用递归的方式,从第 0 行开始,逐行遍历每个位置。对于每个位置,检查当前列、正对角线和反对角线是否已经被占用。如果没有被占用,则将皇后放在该位置,并更新状态数组。然后递归地搜索下一行。当搜索到最后一行时,得到一个可行解,将其保存到结果列表中。最后,恢复当前位置的状态,继续尝试下一个位置。
复杂度分析:
时间复杂度:
- 在递归求解过程中,每行都需要尝试遍历可选位置,时间复杂度为 O(N!)。
- 在每个位置上,需要检查当前列、正对角线和反对角线是否已经被占用,每次检查的时间复杂度为 O(1)。 综上,总的时间复杂度为 O(N * N!).
空间复杂度:
- 递归调用栈的深度为 N,每层递归需要常数级别的额外空间,因此空间复杂度为 O(N)。
- 存储结果列表的空间复杂度为 O(N^2 * N!),其中 N^2 是存储每个解所需的空间。 综上,总的空间复杂度为 O(N^2 * N!).
需要注意的是,尽管在代码中使用了剪枝操作来减少不必要的搜索,但是对于较大的 N,仍然会有大量的组合需要尝试。因此,在实际应用中,当 N 较大时,可能需要考虑其他更加高效的解决方案或优化算法。
LeetCode运行结果:
相关文章:

怒刷LeetCode的第21天(Java版)
目录 第一题 题目来源 题目内容 解决方法 方法一:哈希表 方法二:计数器数组 第二题 题目来源 题目内容 解决方法 方法一:分治法 方法二:快速幂 迭代 方法三:快速幂 递归 第三题 题目来源 题目内容 …...

Armv9 Cortex-A720的L2 memory system 和 L2 Cache
9 L2 memory system Cortex-A720核心的L2内存系统通过CPU bridge连接core与DynamIQ Shared Unit-120,其中包括私有的L2缓存。 L2缓存是统一的,每个Cortex-A720核心在一个集群中都有私有的L2缓存。 L2内存系统包括使用虚拟地址(VA)和程序计数器(PC)的数据预取引擎。不同…...

蓝桥等考Python组别九级003
第一部分:选择题 1、Python L9 (15分) 运行下面程序,可以输出几行“*”?( ) for i in range(3): for j in range(4): print(*, end = ) print() 6374正确答案:B 2、Python L9...
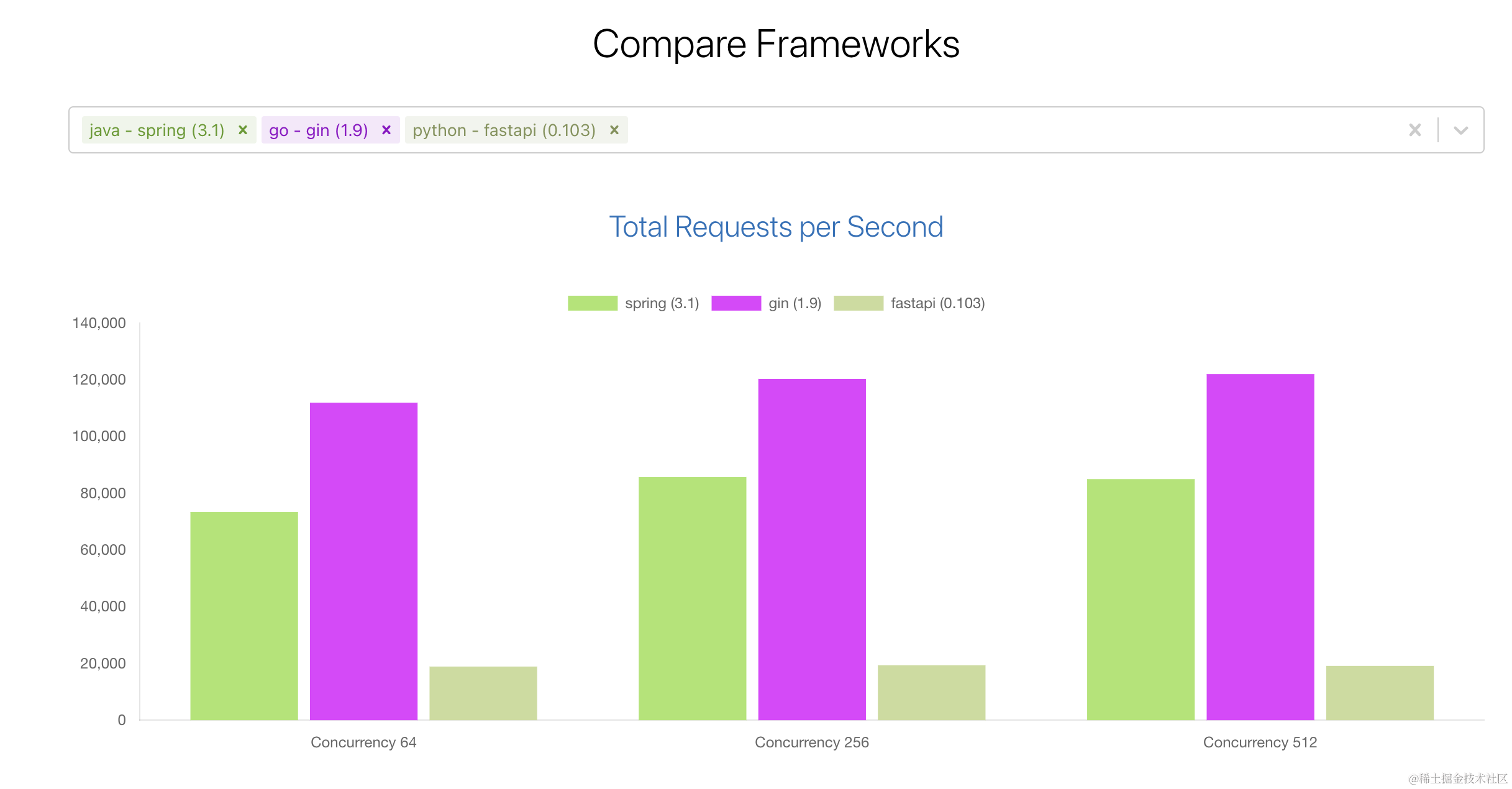
Python异步框架大战:FastAPI、Sanic、Tornado VS Go 的 Gin
一、前言 异步编程在构建高性能 Web 应用中起着关键作用,而 FastAPI、Sanic、Tornado 都声称具有卓越的性能。本文将通过性能压测对这些框架与Go的Gin框架进行全面对比,揭示它们之间的差异。 原文:Python异步框架大战:FastAPI、Sa…...

Docker笔记1
一、Docker介绍 Docker是一个开源的应用容器引擎,基于Go语言并遵从Apache2.0协议开源 可以让开发者打包他们的应用以及依赖包到一个轻量级、可移植的容器中,然后发布到任何流行的Linux机器上,也可以实现虚拟化。 容器是完全使用沙箱机制&a…...
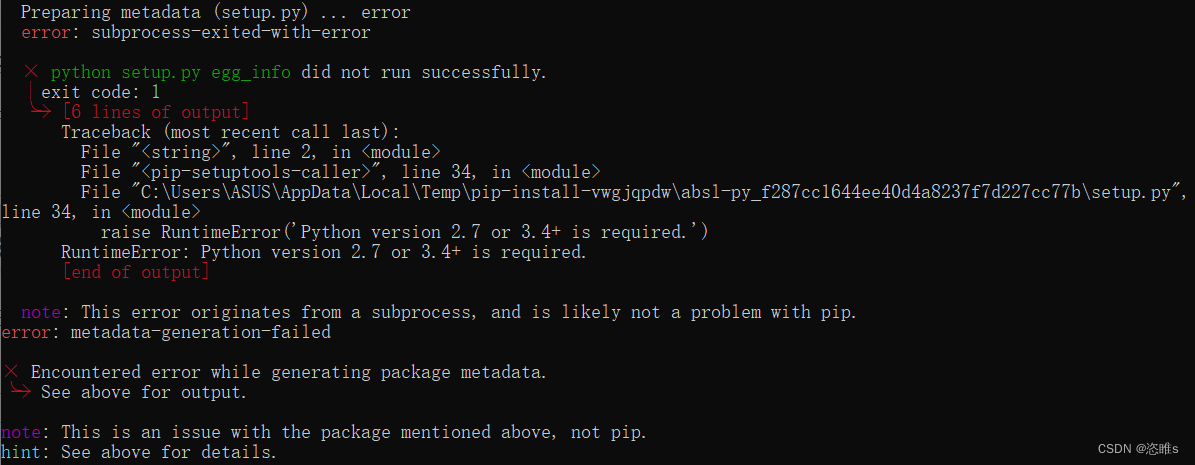
TensorFlow-Federated简介与安装
1、简介 TensorFlow Federated(TFF)是一个用于机器学习和其他分布式数据计算的开源框架。TFF 的开发旨在促进联邦学习 (FL)的开放研究和实验。联邦学习是一种机器学习方法,其中一个共享的全局模型在许多参与的客户之间…...

【强化学习】基础概念
1. Agent (智能体) 智能体是进行决策和学习的实体,它能感知环境的状态,并基于策略采取动作以影响环境。智能体的目标是通过与环境的交互获得最大化的累积奖励。 2. Environment (环境) 环境是智能体所处的外部系统,它与智能体交互。环境的…...

云原生Kubernetes:K8S集群各组件服务重启
目录 一、理论 1.各组件服务重启命令 一、理论 1.各组件服务重启命令 (1)Master节点Node节点共同服务 systemctl restart etcd systemctl daemon-reload systemctl enable flanneld systemctl restart flanneld (2)Master节…...

闲话Python编程-循环
1. for循环 Python的for语句有点特别,只能对序列和字符串进行处理,序列自然包括list、tuple和range对象。 #!/usr/bin/env python3 # -*- coding: utf-8 -*- # 练习for语句def loop_for():names [Tom, Jack, Black]for name in names:print(name)s ab…...

建筑能源管理(3)——建筑能源监管
为了全面落实科学发展观,提高建筑能源管理水平,进一步降低能源和水资源消耗、合理利用资源,以政府办公建筑和大型公共建筑的运行节能管理为突破口,建立了既有政府办公建筑和大型公共建筑运行节能监管体系,旨在提高政府…...
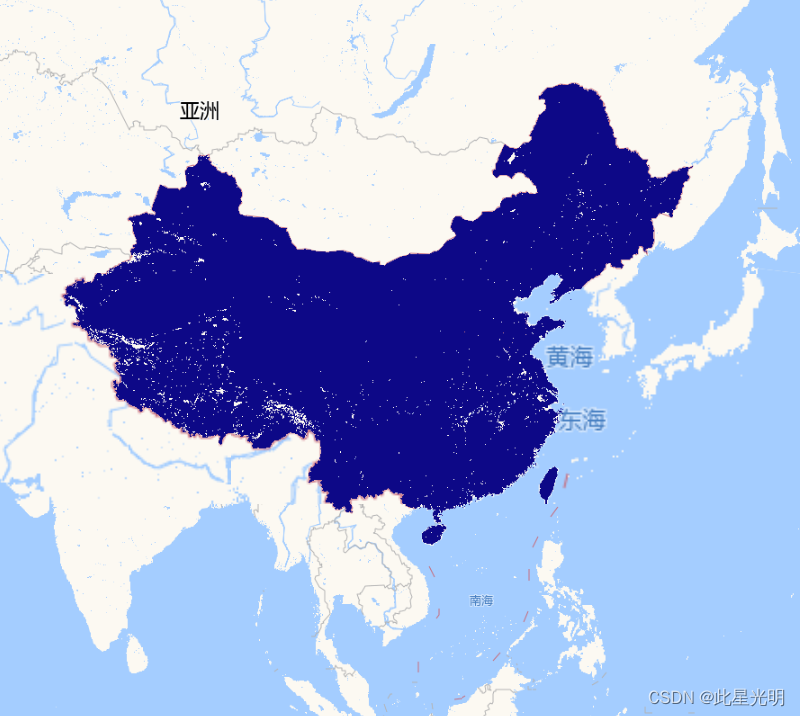
中国逐年干燥度指数数据集
简介: 中国逐年干燥度指数,空间分辨率为1km,时间为1901-2022,为比值,没有单位。该数据集是基于中国1km逐月潜在蒸散发(PET)和降水量(PRE)采用比值法计算式得到ÿ…...

Azure Arc 概要:功能、管理和应用场景详解,AZ900 考点示例
文章目录 本文大纲一、什么是 Azure Arc二、使用 Azure Arc 可以做什么操作三、使用 Azure Arc 可以管理什么资源3.1 如何使用Azure Arc与服务器? 四、Azure Arc 支持的主要场景五、在 AZ900 中的考点示例5.1 示例题 15.2 示例题 2 本文大纲 本文思维导图概述的主要内容&…...
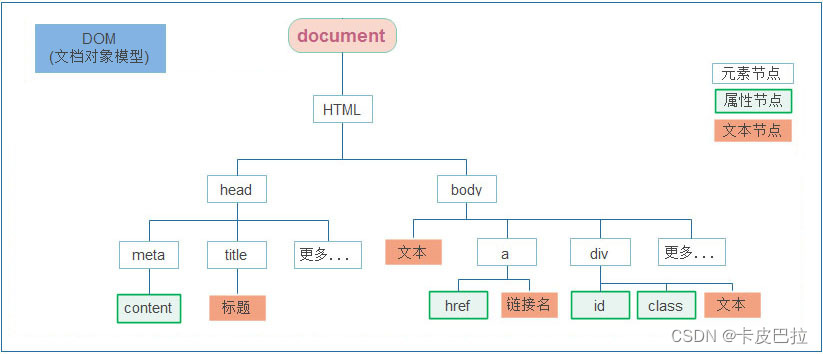
JavaScript Web APIs第一天笔记
复习: splice() 方法用于添加或删除数组中的元素。 **注意:**这种方法会改变原始数组。 删除数组: splice(起始位置, 删除的个数) 比如:1 let arr [red, green, blue] arr.splice(1,1) // 删除green元素 consol…...

十六.镜头知识之工业镜头的质量判断因素
十六.镜头知识之工业镜头的质量判断因素 文章目录 十六.镜头知识之工业镜头的质量判断因素1.分辨率(Resolution)2.明锐度(Acutance)3.景深(DOF):4. 最大相对孔径与光圈系数5.工业镜头各参数间的相互影响关系5.1.焦距大小的影响情况5.2.光圈大小的影响情况5.3.像场中…...

网络协议--概述
1.2 分层 网络协议通常分不同层次进行开发,每一层分别负责不同的通信功能。一个协议族,比如TCP/IP,是一组不同层次上的多个协议的组合。 TCP/IP通常被认为是一个四层协议系统,如图1-1所示。每一层负责不同的功能: 1.链…...

aarch64 平台 musl gcc 工具链手动编译方法
目标 手动编译一个 aarch64 平台的 musl gcc 工具链 musl libc 与 glibc、uclibc 等,都是 标准C 库, musl libc 是基于系统调用之上的 标准C 库,也就是用户态的 标准C 库。 musl libc 轻量、开源、免费,是一些 操作系统的选择,当前 Lite-OS 与 RT-Smart 等均采用自制的 mu…...

计算机图像处理-高斯滤波
高斯滤波 高斯滤波是一种线性平滑滤波,适用于消除高斯噪声,广泛应用于图像处理的减噪过程。通俗的讲,高斯滤波就是对整幅图像进行加权平均的过程,每一个像素点的值,都由其本身和邻域内的其他像素值经过加权平均后得到…...
lv5 嵌入式开发-9 信号机制(上)
目录 1 信号机制 2 信号的产生 3 常用信号 4 相关命令 4.1 信号相关命令 kill / killall 4.2 信号发送 – kill / raise 4.3 定时器函数相关函数 – alarm /ualarm/ pause 4.4 信号捕捉:设置信号响应方式 – signal /sigaction,闹钟实现 4.5 子…...

460. LFU 缓存
请你为 最不经常使用(LFU)缓存算法设计并实现数据结构。 实现 LFUCache 类: LFUCache(int capacity) - 用数据结构的容量 capacity 初始化对象int get(int key) - 如果键 key 存在于缓存中,则获取键的值,否则返回 -1…...

YOLOV8 C++ opecv_dnn模块部署
废话不多说:opencv>4.7.0 opencv编译不做解释,需要的话翻看别的博主的编译教程 代码饱含V5,V7,V8部署内容 头文件yoloV8.h #pragma once #include<iostream> #include<opencv2/opencv.hpp> using namespace std; using namespace cv; using name…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

RabbitMQ入门4.1.0版本(基于java、SpringBoot操作)
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发,后来由Pivotal Software Inc.(现为VMware子公司)接管。RabbitMQ 是一个开源的消息代理和队列服务器,用 Erlang 语言编写。广泛应用于各种分布…...

MySQL 8.0 事务全面讲解
以下是一个结合两次回答的 MySQL 8.0 事务全面讲解,涵盖了事务的核心概念、操作示例、失败回滚、隔离级别、事务性 DDL 和 XA 事务等内容,并修正了查看隔离级别的命令。 MySQL 8.0 事务全面讲解 一、事务的核心概念(ACID) 事务是…...

MacOS下Homebrew国内镜像加速指南(2025最新国内镜像加速)
macos brew国内镜像加速方法 brew install 加速formula.jws.json下载慢加速 🍺 最新版brew安装慢到怀疑人生?别怕,教你轻松起飞! 最近Homebrew更新至最新版,每次执行 brew 命令时都会自动从官方地址 https://formulae.…...
