【算法导论】快速排序
文章目录
- 1. 快速排序的描述
- 1.1基本描述
- 1.2 PARTITOION函数
- 1.3 快速排序C++完整代码
- 2. 快速排序的性能
- 2.1 最坏时间复杂度
- 2.2 平均时间复杂度
1. 快速排序的描述
1.1基本描述
快速排序是一种时间复杂度为 O(n^2) 的排序算法。虽然最坏情况时间复杂度很差,但他的平均性能却很好,它的期望时间复杂度是 O(nlgn) 而且 O(nlgn) 中隐含的常数因子很小大约是1.44左右。
快速排序与归并排序一样,也是基于归并的思想以下是对其子数组 A[ p…r ] 进行快速排序三步分治的过程:
分解:数组 A[ p…r ] 被划分为两个子数组 A[ p…q-1] 和 A[q+1…r],使得 A[ p…q-1]中的每一个元素都小于等于 A[ q ] ,而 A[ q ]也小于等于 A[ q+1…r]中的每一个元素。
解决:通过递归调用快速排序,对子数组A[ p…q-1] 和 A[q+1…r]进行排序。
合并:因为子数组都是原址排序的,所以并不需要合并操作:A[ p…r ] 已经有序。
快速排序伪代码:
QUICKSORT(A,p,r)if p < rq = PARTITION(A, p ,r)QUICKSORT(A, p ,q-1)QUICKSORT(A, q+1 ,r)
其中,q = PARTITION(A, p ,r) 所执行的操作就是分解操作,并返回 q。
1.2 PARTITOION函数
PARTITION函数伪代码:
PARTITION(A, p, r) x = A[r] i = p - 1 for j = p to r - 1 do if A[j] ≤ xthen i = i + 1 exchange A[i] with A[j]
exchange A[i + 1] with A[r]
return i + 1
PARTITION函数思路简介:
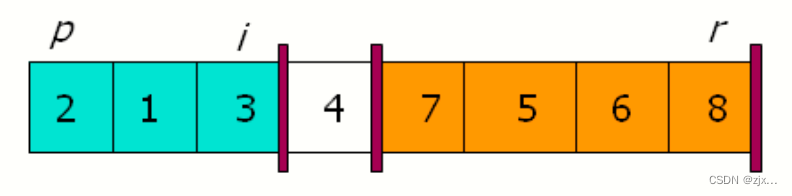
其中 0 - i 维护的是小于等于A[ r ] 的序列,A[ i+1 ] 即为比 A[ r ] 大的第一个数,j从开始节点遍历到倒数第二个节点,遇到比 A[ r ] 小的数便进行 A[ j ] 与 A[ i+1 ] 的交换,以此维护了 0 - i 序列中比 A[ r ]小的特性。j 遍历完成后,即实现了A[0…i] 小于等于 A[ r ] ,A[i+1…j] 大于 A[ r ]。
PARTITION函数执行过程:








1.3 快速排序C++完整代码
# include <iostream>
using namespace std;
int PARTITION(int A[],int p,int r)
{int x = A[r];int i = p - 1;for(int j = p; j <= r - 1; j++){if(A[j] <= x){i = i + 1;swap(A[i],A[j]);}}swap(A[i+1] , A[r]);return i+1;
}
void QUICKSORT(int A[],int p,int r)
{if(p < r){int q = PARTITION(A,p,r);QUICKSORT(A,p,q-1);QUICKSORT(A,q+1,r);}
}
int main()
{int A[100010];int n;cin>>n;for(int i=0;i<n;i++){cin>>A[i];}QUICKSORT(A,0,n-1);for(int i=0;i<n;i++){cout<<A[i]<<" ";}return 0;
}
2. 快速排序的性能
2.1 最坏时间复杂度
因为无法举出使快速排序达到最坏情况的例子所以我们通过两步证明其最坏时间复杂度为 O( n^2 )
- 举一个例子证明其时间复杂度为 O( n 2 n^2 n2)
当对快速排序进行分解的过程中得到的结果为一部分为 n 个元素,另一部分为0个元素时,该例的运行时间递归式为:
T ( n ) = T ( n − 1 ) + T ( 0 ) + θ ( n ) = T ( n − 1 ) + θ ( n ) \begin{aligned}T(n) &= T(n-1)+T(0)+\theta(n)\\ &= T(n-1)+\theta(n) \end{aligned} T(n)=T(n−1)+T(0)+θ(n)=T(n−1)+θ(n)可以得到: T ( n ) = θ ( n 2 ) T(n)=\theta(n^2) T(n)=θ(n2)
由此可知, Quicksort 的最坏运行时间为: Ω( n 2 n^2 n2) - 证明其时间复杂度不超过 O( n 2 n^2 n2)
设T(n)是对大小为 n 的输入进行快速排序的最坏情况时间,则有递归:
T ( n ) = max 0 ≤ q ≤ n − 1 ( T ( q ) + T ( n − q − 1 ) ) + C 1 n T(n)=\max_{0 \leq q\leq n-1}(T(q)+T(n-q-1))+C_1n T(n)=0≤q≤n−1max(T(q)+T(n−q−1))+C1n我们猜测对于某个常数C使得T (n) ≤ C,将这个猜测代入上面的递推式,我们得到:
T ( n ) ≤ max 0 ≤ q ≤ n − 1 ( C q 2 + C ( n − q − 1 ) 2 ) + C 1 n = C ∗ max 0 ≤ q ≤ n − 1 ( q 2 + ( n − 1 − q ) 2 ) + C 1 n \begin{aligned}T(n)&\leq \max_{0 \leq q\leq n-1}(Cq^2+C(n-q-1)^2)+C_1n\\&=C* \max_{0 \leq q\leq n-1}(q^2+(n-1-q)^2)+C_1n\end{aligned} T(n)≤0≤q≤n−1max(Cq2+C(n−q−1)2)+C1n=C∗0≤q≤n−1max(q2+(n−1−q)2)+C1n由于 q 2 + ( n − 1 − q ) 2 q^2+(n-1-q)^2 q2+(n−1−q)2 是 q q q 的二次函数,求导可得,在区间 [1… n ] 范围内该函数只可能在 q = 1 , q = n , q = n / 4 q = 1,q = n,q = n/4 q=1,q=n,q=n/4,等三个点处取极值,由此可知:
∑ 0 ≤ q ≤ n − 1 ( q 2 + ( n − 1 − q ) 2 ) ≤ n 2 \sum_{0 \leq q\leq n-1}(q^2+(n-1-q)^2) \leq n^2 0≤q≤n−1∑(q2+(n−1−q)2)≤n2所以有:
T ( n ) ≤ C ( n − 1 ) 2 + C 1 n = C ∗ n 2 − 2 C n + C 1 n + C T(n)\leq C(n-1)^2+C_1n=C*n^2-2Cn+C_1n+C T(n)≤C(n−1)2+C1n=C∗n2−2Cn+C1n+C当取 C > C1 时, T ( n ) < = C n 2 T (n)<=Cn^2 T(n)<=Cn2 对所有 n > = 1 n >=1 n>=1 成立,由此证得快速排序时间复杂度不超过 O( n 2 n^2 n2)。
2.2 平均时间复杂度
设 T ( n ) T (n) T(n) 为输入规模为 n 时 QUICKSORT 算法的平均运行时间, T k ( n ) T_k(n) Tk(n)为所选划分元序号为 k+1 时 QUICKSORT 算法的平均运行时间,则 T ( n ) T (n) T(n) 满足以下递归方程:
T ( n ) = ∑ k = 0 n − 1 ( p ( k + 1 ) T k ( n ) ) T(n)=\sum_{k=0}^{n-1} (p(k+1)T_k(n)) T(n)=k=0∑n−1(p(k+1)Tk(n))其中 p ( k + 1 ) p(k+1) p(k+1)为划分元素序号为 k + 1 k+1 k+1的概率,我们可以知道划分元素序号的概率是相同的故: p ( k + 1 ) = 1 n p(k+1)=\frac{1}{n} p(k+1)=n1,带入上式可得:
T ( n ) = ∑ k = 0 n − 1 1 n T k ( n ) ) = 1 n ∑ k = 0 n − 1 ( T ( k ) + T ( n − k − 1 ) + c n ) T(n)=\sum_{k=0}^{n-1} \frac{1}{n}T_k(n))= \frac{1}{n}\sum_{k=0}^{n-1} (T(k)+T(n-k-1)+cn) T(n)=k=0∑n−1n1Tk(n))=n1k=0∑n−1(T(k)+T(n−k−1)+cn)继续化简可得:
1 n ( ∑ k = 0 n − 1 T ( k ) + ∑ k = 0 n − 1 T ( n − k − 1 ) ) + c n = 2 n ∑ k = 0 n − 1 T ( k ) + c n \frac{1}{n}(\sum_{k=0}^{n-1} T(k)+\sum_{k=0}^{n-1}T(n-k-1))+cn=\frac{2}{n}\sum_{k=0}^{n-1}T(k)+cn n1(k=0∑n−1T(k)+k=0∑n−1T(n−k−1))+cn=n2k=0∑n−1T(k)+cn解递归方程可得:
n T ( n ) = 2 ∑ k = 0 n − 1 T ( k ) + c n 2 nT(n)=2\sum_{k=0}^{n-1}T(k)+cn^2 nT(n)=2k=0∑n−1T(k)+cn2 ( n − 1 ) T ( n − 1 ) = 2 ∑ k = 0 n − 1 T ( k ) + c n 2 (n-1)T(n-1)=2\sum_{k=0}^{n-1}T(k)+cn^2 (n−1)T(n−1)=2k=0∑n−1T(k)+cn2两式相减,可得:
n T ( n ) − ( n − 1 ) T ( n − 1 ) = 2 T ( n − 1 ) + c ( 2 n − 1 ) nT(n)-(n-1)T(n-1)=2T(n-1)+c(2n-1) nT(n)−(n−1)T(n−1)=2T(n−1)+c(2n−1) T ( n ) n + 1 < = T ( n − 1 ) n + 2 c n \frac{T(n)}{n+1}<=\frac{T(n-1)}{n}+\frac{2c}{n} n+1T(n)<=nT(n−1)+n2c令
G ( n ) = T ( n ) ( n + 1 ) G(n) = \frac{T(n)}{(n+1)} G(n)=(n+1)T(n)则有:
G ( n ) ≤ C ( n − 1 ) + 2 c n = G ( n − 2 ) + 2 c ( 1 n − 1 + 1 n ) = G ( n − 3 ) + 2 c ( 1 n − 2 + 1 n − 1 + 1 n ) = G ( n − k ) + 2 c ( 1 n − k + 1 + . . . + 1 n − 1 + 1 n ) \begin{aligned}G(n)& \leq C(n-1)+\frac{2c}{n}\\&=G(n-2)+2c(\frac{1}{n-1}+\frac{1}{n})\\&=G(n-3)+2c(\frac{1}{n-2}+\frac{1}{n-1}+\frac{1}{n})\\&=G(n-k)+2c(\frac{1}{n-k+1}+...+\frac{1}{n-1}+\frac{1}{n}) \end{aligned} G(n)≤C(n−1)+n2c=G(n−2)+2c(n−11+n1)=G(n−3)+2c(n−21+n−11+n1)=G(n−k)+2c(n−k+11+...+n−11+n1)整理后得到: G ( 1 ) + 2 c ∑ k = 0 n − 2 1 n − k = 2 c ∑ k = 2 n 1 k < = 2 c ∗ H n < = 2 c l o g n G(1)+2c\sum_{k=0}^{n-2}\frac{1}{n-k}=2c\sum_{k=2}^{n}\frac{1}{k}<=2c*H_n<=2clogn G(1)+2ck=0∑n−2n−k1=2ck=2∑nk1<=2c∗Hn<=2clogn
所以,Quicksort 算法的平均时间复杂度为: T ( n ) = G ( n ) ( n + 1 ) = θ ( n l o g n ) T(n)=G(n)(n+1)=\theta(nlogn) T(n)=G(n)(n+1)=θ(nlogn)
相关文章:

【算法导论】快速排序
文章目录 1. 快速排序的描述 1.1基本描述1.2 PARTITOION函数1.3 快速排序C完整代码 2. 快速排序的性能2.1 最坏时间复杂度2.2 平均时间复杂度 1. 快速排序的描述 1.1基本描述 快速排序是一种时间复杂度为 O(n^2) 的排序算法。虽然最坏情况时间复杂度很差,但他的平…...

QT之QScriptEngine的用法介绍
QT之QScriptEngine的用法介绍 成员函数用法举例 成员函数 1)QScriptEngine::evaluate(const QString &program, const QString &fileName QString(), int lineNumber 1) 执行 JavaScript 代码并返回结果。 2)QScriptEngine::evaluate(const…...

vim 工具的使用
注:以下操作都在普通模式下进行 光标的移动操作 gg 定位到代码的第一行 shiftg 定位到代码的最后一行 nshiftg 定位到第n行 shift6: 特定一行的开始 shift4 特定一行的结尾 上下左右的移动光标 h: 向左移动光标 j: 向下移动光标 k: 向上移动光标 l: 向右移动光标 …...

RPA有什么优势?RPA的8大优势!建议学习!
随着科技的不断发展,越来越多的企业开始寻求数字化转型,以提高生产力和效率。在这个过程中,RPA(Robotic Process Automation)机器人流程自动化技术逐渐成为企业数字化转型的重要工具之一。本文将从八个方面阐述RPA的优…...
初级篇—第二章SELECT查询语句
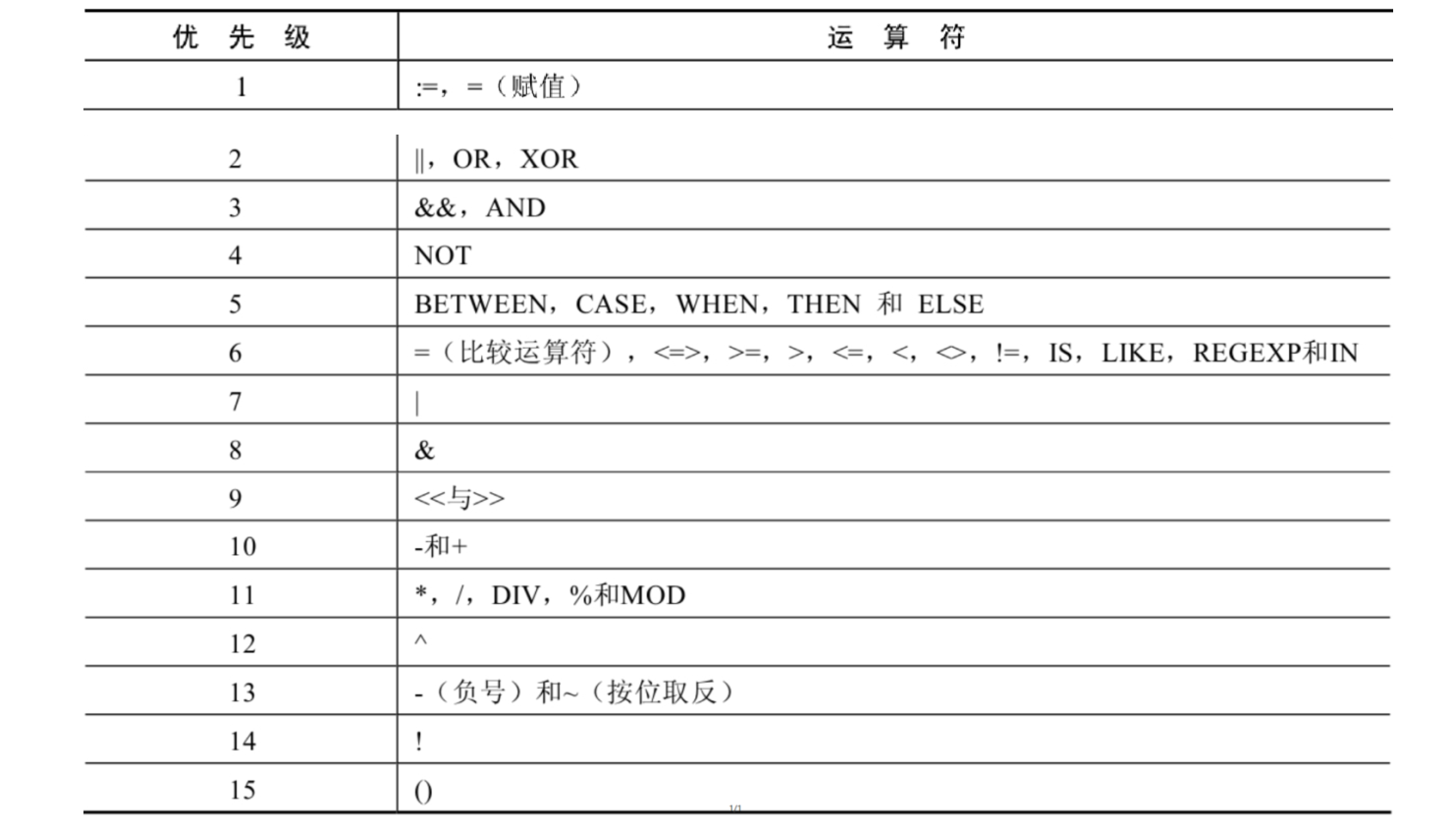
文章目录 什么是SQLSQL 分类SQL语言的规则与规范阿里巴巴MySQL命名规范数据导入指令 显示表结构 DESC基本的SELECT语句SELECTSELECT ... FROM列的别名 AS去除重复行 DISTINCT空值参与运算着重号查询常数过滤数据 WHERE练习 运算符算术运算符加减符号乘除符号取模符号 符号比较运…...

PostMan的学习
PostMan的学习 目录 环境变量和全局变量接口关联内置动态参数以及自定义动态参数实现业务闭环Postman断言批量运行collection数据驱动之CSV文件和JSON文件测试必须带请求头的接口Mock Serviers 服务器Cookie鉴权NewmanPostManNewManjenkins实现接口测试持续集成 参考资料&am…...

配置OSPF路由
OSPF路由 1.OSPF路由 1.1 OSPF简介 OSPF(Open Shortest Path First,开放式最短路径优先)路由协议是另一个比较常用的路由协议之一,它通过路由器之间通告网络接口的状态,使用最短路径算法建立路由表。在生成路由表时,…...

CCF CSP认证 历年题目自练Day17
CCF CSP认证 历年题目自练Day17 题目一 试题编号: 201803-1 试题名称: 跳一跳 时间限制: 1.0s 内存限制: 256.0MB 问题描述: 问题描述 近来,跳一跳这款小游戏风靡全国,受到不少玩家的喜爱…...
)
基于Matlab实现多因子选股模型(附上源码+数据)
本文将介绍如何使用MATLAB实现多因子选股模型。我们将使用市盈率和市净率两个因子来进行选股,并通过简单的代码案例来演示该过程。 文章目录 引言简单案例总结源码数据下载 引言 多因子选股模型是一种常用的股票选股方法,通过综合考虑多个因子的信息来…...

【中秋国庆不断更】OpenHarmony多态样式stateStyles使用场景
Styles和Extend仅仅应用于静态页面的样式复用,stateStyles可以依据组件的内部状态的不同,快速设置不同样式。这就是我们本章要介绍的内容stateStyles(又称为:多态样式)。 概述 stateStyles是属性方法,可以根…...
Qt扩展-QCustomPlot绘图基础概述
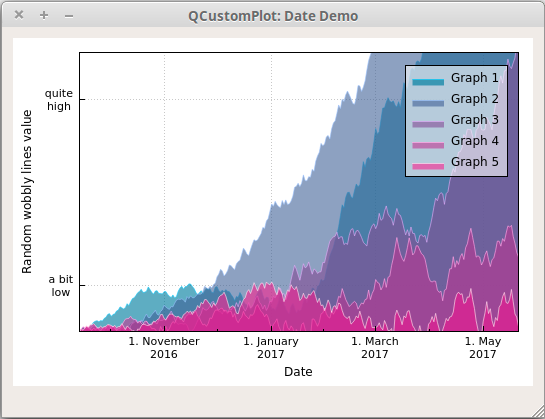
QCustomPlot绘图基础概述 一、概述二、改变外观1. Graph 类型2. Axis 坐标轴3. 网格 三、案例1. 简单布局两个图2. 绘图与多个轴和更先进的样式3. 绘制日期和时间数据 四、其他Graph:曲线,条形图,统计框图,… 一、概述 本教程使用…...
二、局域网联机
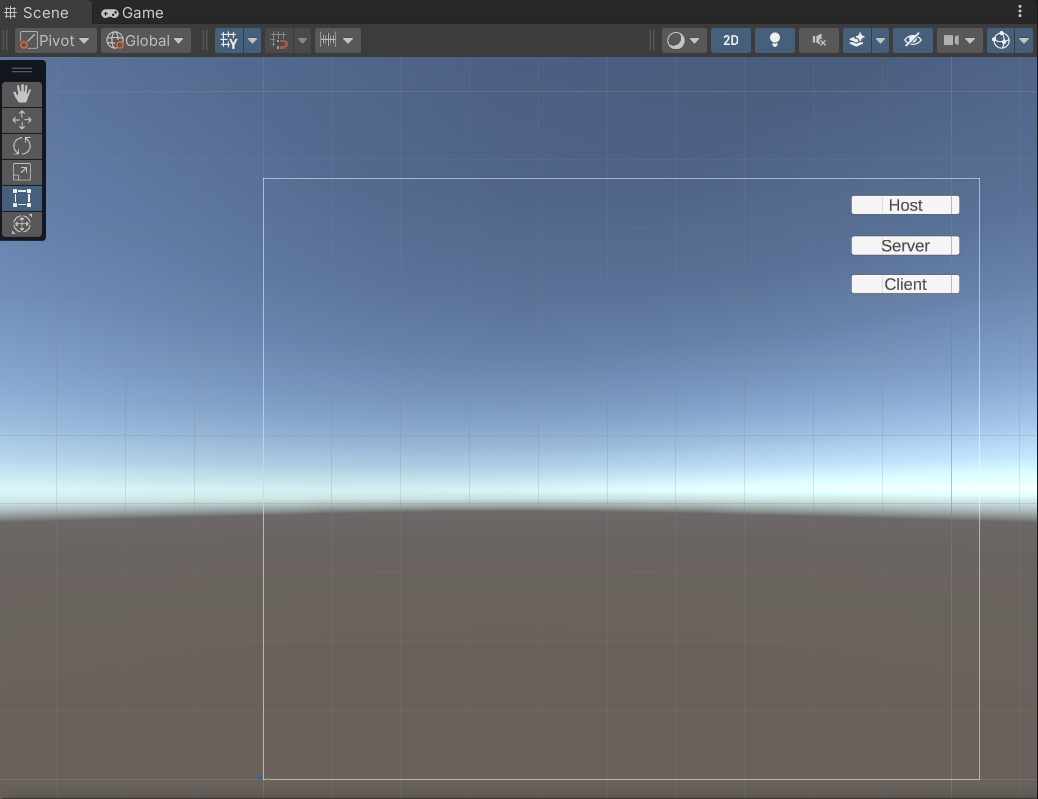
目录 1.下载资源包 2.配置NetworkManager 3.编写测试UI 1.下载资源包 2.配置NetworkManager (1)在Assets/Prefabs下创建Network Prefabs List 相应设置如下: (2) 创建空物体“NetworkManager”并挂载NetworkMan…...

决策树剪枝:解决模型过拟合【决策树、机器学习】
如何通过剪枝解决决策树的过拟合问题 决策树是一种强大的机器学习算法,用于解决分类和回归问题。决策树模型通过树状结构的决策规则来进行预测,但在构建决策树时,常常会出现过拟合的问题,即模型在训练数据上表现出色,…...

Ubuntu部署运行ORB-SLAM2
ORB-SLAM2是特征点法的视觉SLAM集大成者,不夸张地说是必学代码。博主已经多次部署运行与ORB-SLAM2相关的代码,所以对环境和依赖很熟悉,对整个系统也是学习了几个月,一行行代码理解。本次在工控机上部署记录下完整的流程。 ORB-SLA…...
二十,镜面IBL--打印BRDF积分贴图
比起以往,这节应该是最轻松的了, 运行结果如下 代码如下: #include <osg/TextureCubeMap> #include <osg/TexGen> #include <osg/TexEnvCombine> #include <osgUtil/ReflectionMapGenerator> #include <osgDB/Re…...

自动驾驶:未来的道路上的挑战与机遇
自动驾驶:未来的道路上的挑战与机遇 文章目录 引言安全与道路事故的减少交通拥堵的缓解城市规划的变革技术和法律挑战结语 2023星火培训【专项营】Apollo开发者社区布道师倾力打造,包含PnC、新感知等的全新专项课程上线了。理论与实践相结合,…...

Go 语言 iota 的神奇力量
前言 当你深入研究官网库、开源库或者任何一个 Go 项目时,你都会发现 iota 这个神奇的标识符无处不在。它扮演着一种重要的角色,让代码变得更加简洁、清晰,并提高了可读性和可维护性。它的应用范围广泛,从枚举类型到位运算&#…...

前端开发和后端开发的一些建议
前端开发和后端开发是Web开发的两个方向 前端开发主要负责实现用户在浏览器上看到的界面和交互体验,包括HTML、CSS和JavaScript等技术。后端开发主要负责处理服务器端的逻辑和数据,包括数据库操作、服务器配置和接口开发等技术。 前端开发 前端开发需…...
基于 SpringBoot+Vue 的教室人事档案管理系统
1 简介 教师人事档案管理系统利用信息的合理管理,动态的、高效的、安全的实现了教师的各种需求,改变了传统的网上查看方式,使教师可以足不出户的在线查看最适合自己个人档案、奖惩信息、档案变动、培训报名或者新闻资讯。 1、教师后台功能模…...

Lua学习笔记:require非.lua拓展名的文件
前言 本篇在讲什么 Lua的require相关的内容 本篇需要什么 对Lua语法有简单认知 对C语法有简单认知 依赖Visual Studio工具 本篇的特色 具有全流程的图文教学 重实践,轻理论,快速上手 提供全流程的源码内容 ★提高阅读体验★ 👉 ♠…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...
中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

Yolov8 目标检测蒸馏学习记录
yolov8系列模型蒸馏基本流程,代码下载:这里本人提交了一个demo:djdll/Yolov8_Distillation: Yolov8轻量化_蒸馏代码实现 在轻量化模型设计中,**知识蒸馏(Knowledge Distillation)**被广泛应用,作为提升模型…...
