[NOIP2012 提高组] 开车旅行
[NOIP2012 提高组] 开车旅行
题目描述
小 A \text{A} A 和小 B \text{B} B 决定利用假期外出旅行,他们将想去的城市从 $1 $ 到 n n n 编号,且编号较小的城市在编号较大的城市的西边,已知各个城市的海拔高度互不相同,记城市 i i i 的海拔高度为 h i h_i hi,城市 i i i 和城市 j j j 之间的距离 d i , j d_{i,j} di,j 恰好是这两个城市海拔高度之差的绝对值,即 d i , j = ∣ h i − h j ∣ d_{i,j}=|h_i-h_j| di,j=∣hi−hj∣。
旅行过程中,小 A \text{A} A 和小 B \text{B} B 轮流开车,第一天小 A \text{A} A 开车,之后每天轮换一次。他们计划选择一个城市 s s s 作为起点,一直向东行驶,并且最多行驶 x x x 公里就结束旅行。
小 A \text{A} A 和小 B \text{B} B 的驾驶风格不同,小 B \text{B} B 总是沿着前进方向选择一个最近的城市作为目的地,而小 A \text{A} A 总是沿着前进方向选择第二近的城市作为目的地(注意:本题中如果当前城市到两个城市的距离相同,则认为离海拔低的那个城市更近)。如果其中任何一人无法按照自己的原则选择目的城市,或者到达目的地会使行驶的总距离超出 x x x 公里,他们就会结束旅行。
在启程之前,小 A \text{A} A 想知道两个问题:
1、 对于一个给定的 x = x 0 x=x_0 x=x0,从哪一个城市出发,小 A \text{A} A 开车行驶的路程总数与小 B \text{B} B 行驶的路程总数的比值最小(如果小 B \text{B} B 的行驶路程为 0 0 0,此时的比值可视为无穷大,且两个无穷大视为相等)。如果从多个城市出发,小 A \text{A} A 开车行驶的路程总数与小 B \text{B} B 行驶的路程总数的比值都最小,则输出海拔最高的那个城市。
2、对任意给定的 x = x i x=x_i x=xi 和出发城市 s i s_i si,小 A \text{A} A 开车行驶的路程总数以及小 B \text B B 行驶的路程总数。
输入格式
第一行包含一个整数 n n n,表示城市的数目。
第二行有 n n n 个整数,每两个整数之间用一个空格隔开,依次表示城市 1 1 1 到城市 n n n 的海拔高度,即 h 1 , h 2 . . . h n h_1,h_2 ... h_n h1,h2...hn,且每个 h i h_i hi 都是互不相同的。
第三行包含一个整数 x 0 x_0 x0。
第四行为一个整数 m m m,表示给定 m m m 组 s i s_i si 和 x i x_i xi。
接下来的 m m m 行,每行包含 2 2 2 个整数 s i s_i si 和 x i x_i xi,表示从城市 s i s_i si 出发,最多行驶 x i x_i xi 公里。
输出格式
输出共 m + 1 m+1 m+1 行。
第一行包含一个整数 s 0 s_0 s0,表示对于给定的 x 0 x_0 x0,从编号为 s 0 s_0 s0 的城市出发,小 A \text A A 开车行驶的路程总数与小 B \text B B 行驶的路程总数的比值最小。
接下来的 m m m 行,每行包含 2 2 2 个整数,之间用一个空格隔开,依次表示在给定的 s i s_i si 和 x i x_i xi 下小 A \text A A 行驶的里程总数和小 B \text B B 行驶的里程总数。
样例 #1
样例输入 #1
4
2 3 1 4
3
4
1 3
2 3
3 3
4 3
样例输出 #1
1
1 1
2 0
0 0
0 0
样例 #2
样例输入 #2
10
4 5 6 1 2 3 7 8 9 10
7
10
1 7
2 7
3 7
4 7
5 7
6 7
7 7
8 7
9 7
10 7
样例输出 #2
2
3 2
2 4
2 1
2 4
5 1
5 1
2 1
2 0
0 0
0 0
提示
【样例1说明】
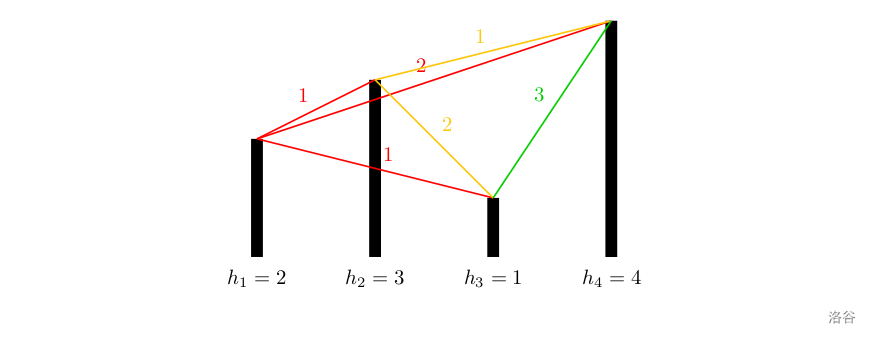
各个城市的海拔高度以及两个城市间的距离如上图所示。
如果从城市 1 1 1 出发,可以到达的城市为 2 , 3 , 4 2,3,4 2,3,4,这几个城市与城市 1 1 1 的距离分别为 1 , 1 , 2 1,1,2 1,1,2,但是由于城市 3 3 3 的海拔高度低于城市 2 2 2,所以我们认为城市 3 3 3 离城市 1 1 1 最近,城市 2 2 2 离城市 1 1 1 第二近,所以小A会走到城市 2 2 2。到达城市 2 2 2 后,前面可以到达的城市为 3 , 4 3,4 3,4,这两个城市与城市 2 2 2 的距离分别为 2 , 1 2,1 2,1,所以城市 4 4 4 离城市 2 2 2 最近,因此小B会走到城市 4 4 4。到达城市 4 4 4 后,前面已没有可到达的城市,所以旅行结束。
如果从城市 2 2 2 出发,可以到达的城市为 3 , 4 3,4 3,4,这两个城市与城市 2 2 2 的距离分别为 2 , 1 2,1 2,1,由于城市 3 3 3 离城市 2 2 2 第二近,所以小 A \text A A 会走到城市 3 3 3。到达城市 3 3 3 后,前面尚未旅行的城市为 4 4 4,所以城市 4 4 4 离城市 3 3 3 最近,但是如果要到达城市 4 4 4,则总路程为 2 + 3 = 5 > 3 2+3=5>3 2+3=5>3,所以小 B \text B B 会直接在城市 3 3 3 结束旅行。
如果从城市 3 3 3 出发,可以到达的城市为 4 4 4,由于没有离城市 3 3 3 第二近的城市,因此旅行还未开始就结束了。
如果从城市 4 4 4 出发,没有可以到达的城市,因此旅行还未开始就结束了。
【样例2说明】
当 x = 7 x=7 x=7 时,如果从城市 1 1 1 出发,则路线为 1 → 2 → 3 → 8 → 9 1 \to 2 \to 3 \to 8 \to 9 1→2→3→8→9,小 A \text A A 走的距离为 1 + 2 = 3 1+2=3 1+2=3,小 B \text B B 走的距离为 1 + 1 = 2 1+1=2 1+1=2。(在城市 1 1 1 时,距离小 A \text A A 最近的城市是 2 2 2 和 6 6 6,但是城市 2 2 2 的海拔更高,视为与城市 1 1 1 第二近的城市,所以小 A \text A A 最终选择城市 2 2 2;走到 9 9 9 后,小 A \text A A 只有城市 10 10 10 可以走,没有第二选择可以选,所以没法做出选择,结束旅行)
如果从城市 2 2 2 出发,则路线为 2 → 6 → 7 2 \to 6 \to 7 2→6→7,小 A \text A A 和小 B \text B B 走的距离分别为 2 , 4 2,4 2,4。
如果从城市 3 3 3 出发,则路线为 3 → 8 → 9 3 \to 8 \to 9 3→8→9,小 A \text A A 和小 B \text B B 走的距离分别为 2 , 1 2,1 2,1。
如果从城市 4 4 4 出发,则路线为 4 → 6 → 7 4 \to 6 \to 7 4→6→7,小 A \text A A 和小 B \text B B 走的距离分别为 2 , 4 2,4 2,4。
如果从城市 5 5 5 出发,则路线为 5 → 7 → 8 5 \to 7 \to 8 5→7→8,小 A \text A A 和小 B \text B B 走的距离分别为 5 , 1 5,1 5,1。
如果从城市 6 6 6 出发,则路线为 6 → 8 → 9 6 \to 8 \to 9 6→8→9,小 A \text A A 和小 B \text B B 走的距离分别为 5 , 1 5,1 5,1。
如果从城市 7 7 7 出发,则路线为 7 → 9 → 10 7 \to 9 \to 10 7→9→10,小 A \text A A 和小 B \text B B 走的距离分别为 2 , 1 2,1 2,1。
如果从城市 8 8 8 出发,则路线为 8 → 10 8 \to 10 8→10,小 A \text A A 和小 B \text B B 走的距离分别为 2 , 0 2,0 2,0。
如果从城市 9 9 9 出发,则路线为 9 9 9,小 A \text A A 和小 B \text B B 走的距离分别为 0 , 0 0,0 0,0(旅行一开始就结束了)。
如果从城市 10 10 10 出发,则路线为 10 10 10,小 A \text A A 和小 B \text B B 走的距离分别为 0 , 0 0,0 0,0。
从城市 2 2 2 或者城市 4 4 4 出发小 A \text A A 行驶的路程总数与小 B \text B B 行驶的路程总数的比值都最小,但是城市 2 2 2 的海拔更高,所以输出第一行为 2 2 2。
【数据范围与约定】
对于 30 % 30\% 30% 的数据,有 1 ≤ n ≤ 20 , 1 ≤ m ≤ 20 1\le n \le 20,1\le m\le 20 1≤n≤20,1≤m≤20;
对于 40 % 40\% 40% 的数据,有 1 ≤ n ≤ 100 , 1 ≤ m ≤ 100 1\le n \le 100,1\le m\le 100 1≤n≤100,1≤m≤100;
对于 50 % 50\% 50% 的数据,有 1 ≤ n ≤ 100 , 1 ≤ m ≤ 1000 1\le n \le 100,1\le m\le 1000 1≤n≤100,1≤m≤1000;
对于 70 % 70\% 70% 的数据,有 1 ≤ n ≤ 1000 , 1 ≤ m ≤ 1 0 4 1\le n \le 1000,1\le m\le 10^4 1≤n≤1000,1≤m≤104;
对于 100 % 100\% 100% 的数据: 1 ≤ n , m ≤ 1 0 5 1\le n,m \le 10^5 1≤n,m≤105, − 1 0 9 ≤ h i ≤ 1 0 9 -10^9 \le h_i≤10^9 −109≤hi≤109, 1 ≤ s i ≤ n 1 \le s_i \le n 1≤si≤n, 0 ≤ x i ≤ 1 0 9 0 \le x_i \le 10^9 0≤xi≤109
数据保证 h i h_i hi 互不相同。
完整代码
#include<iostream>
#include<cstdio>
#include<cmath>
#include<set>
using namespace std;
const int N=1e5+200,INF=2e9;
struct City
{int id,al;//identifier,altitudefriend bool operator < (City a,City b){return a.al<b.al; }
};
int n,m,x0,la,lb,ansid;
int h[N],s[N],x[N];
int f[20][N][5],da[20][N][5],db[20][N][5];
double ans=INF*1.0;
multiset<City> q;
void calc(int S,int X)
{int p=S;la=0,lb=0;for(int i=18;i>=0;i--)if(f[i][p][0] && la+lb+da[i][p][0]+db[i][p][0]<=X){la+=da[i][p][0];lb+=db[i][p][0];p=f[i][p][0];}
}
void pre()
{h[0]=INF,h[n+1]=-INF;City st;//startst.id=0,st.al=INF;q.insert(st),q.insert(st);st.id=n+1,st.al=-INF;q.insert(st),q.insert(st);for(int i=n;i;i--){int ga,gb;City now;now.id=i,now.al=h[i];q.insert(now);set<City>::iterator p=q.lower_bound(now);p--;int lt=(*p).id,lh=(*p).al;//lastp++,p++;int ne=(*p).id,nh=(*p).al;//nextp--;if(abs(nh-h[i])>=abs(h[i]-lh)){gb=lt;p--,p--;if(abs(nh-h[i])>=abs(h[i]-(*p).al))ga=(*p).id;elsega=ne;}else{gb=ne;p++,p++;if(abs((*p).al-h[i])>=abs(h[i]-lh))ga=lt;elsega=(*p).id;}//2、预处理f[0][i][0]=ga,f[0][i][1]=gb;da[0][i][0]=abs(h[i]-h[ga]);db[0][i][1]=abs(h[i]-h[gb]);//3、DP初值}for(int i=1;i<=18;i++)for(int j=1;j<=n;j++)for(int k=0;k<2;k++)if(i==1){f[1][j][k]=f[0][f[0][j][k]][1-k];da[1][j][k]=da[0][j][k]+da[0][f[0][j][k]][1-k];db[1][j][k]=db[0][j][k]+db[0][f[0][j][k]][1-k]; }else{f[i][j][k]=f[i-1][f[i-1][j][k]][k];da[i][j][k]=da[i-1][j][k]+da[i-1][f[i-1][j][k]][k];db[i][j][k]=db[i-1][j][k]+db[i-1][f[i-1][j][k]][k];}//3、倍增优化DP
}
int main()
{cin>>n;for(int i=1;i<=n;i++)scanf("%d",&h[i]);cin>>x0>>m;for(int i=1;i<=m;i++)scanf("%d%d",&s[i],&x[i]);//1、输入pre();for(int i=1;i<=n;i++){calc(i,x0);double nowans=(double)la/(double)lb;if(nowans<ans){ans=nowans;ansid=i;}elseif(nowans==ans && h[ansid]<h[i])ansid=i;}cout<<ansid<<endl;//4、求解问题1for(int i=1;i<=m;i++){calc(s[i],x[i]);printf("%d %d\n",la,lb);}//5、求解问题2return 0;
}
相关文章:

[NOIP2012 提高组] 开车旅行
[NOIP2012 提高组] 开车旅行 题目描述 小 A \text{A} A 和小 B \text{B} B 决定利用假期外出旅行,他们将想去的城市从 $1 $ 到 n n n 编号,且编号较小的城市在编号较大的城市的西边,已知各个城市的海拔高度互不相同,记城市 …...

数据库设计流程---以案例熟悉
案例名字:宠物商店系统 课程来源:点击跳转 信息->概念模型->数据模型->数据库结构模型 将现实世界中的信息转换为信息世界的概念模型(E-R模型) 业务逻辑 构建 E-R 图 确定三个实体:用户、商品、订单...
Miniconda创建paddlepaddle环境
1、conda env list 2、conda create --name paddle_env python3.8 --channel https://mirrors.tuna.tsinghua.edu.cn/anaconda/pkgs/free/ 3、activate paddle_env 4、python -m pip install paddlepaddle -i https://mirror.baidu.com/pypi/simple 5、pip install "p…...
postgresql实现单主单从
实现步骤 1.主库创建一个有复制权限的用户 CREATE ROLE 用户名login # 有登录权限的角色即是用户replication #复制权限 encrypted password 密码;2.主库配置开放从库外部访问权限 修改 pg_hba.conf 文件 (相当于开放防火墙) # 类型 数据库 …...
提取PDF数据:Documents for PDF ( GcPdf )
在当今数据驱动的世界中,从 PDF 文档中无缝提取结构化表格数据已成为开发人员的一项关键任务。借助GrapeCity Documents for PDF ( GcPdf ),您可以使用 C# 以编程方式轻松解锁这些 PDF 中隐藏的信息宝藏。 考虑一下 PDF(最常用的文档格式之一…...

adb连接切换到模拟器端口
查看连接状态 adb devices出现以下情况 C:\Users\22560>adb devices List of devices attached 127.0.0.1:5555 offline emulator-5554 device可以发现我们想要连接的雷电模拟器的5555端口目前没有连接,只有emulator-5554被连接了,此时我们需要关…...
为何每个开发者都在谈论Go?
目录 一、引言Go的历史回顾关键时间节点 使用场景Go的语言地位技术社群与企业支持资源投入和生态系统 二、简洁的语法结构基本组成元素变量声明与初始化代码示例 类型推断函数与返回值代码示例输出 接口与结构体:组合而非继承错误处理:明确而不是异常小结…...
【Leetcode】 501. 二叉搜索树中的众数
给你一个含重复值的二叉搜索树(BST)的根节点 root ,找出并返回 BST 中的所有 众数(即,出现频率最高的元素)。 如果树中有不止一个众数,可以按 任意顺序 返回。 假定 BST 满足如下定义…...

怎样给Ubuntu系统安装vmware-tools
首先我要告诉你:Ubuntu无法安装vmware-tools,之所以这么些是因为我一开始也是这样认为的,vmware-tools是给Windows系统准备的我认为,毕竟Windows占有率远远高于Linux,这也可以理解。 那么怎么样实现Ubuntu虚拟机跟Wind…...

DDS信号发生器波形发生器VHDL
名称:DDS信号发生器波形发生器 软件:Quartus 语言:VHDL 要求: 在EDA平台中使用VHDL语言为工具,设计一个常见信号发生电路,要求: 1. 能够产生锯齿波,方波,三角波&…...

Python3操作SQLite3创建表主键自增长|CRUD基本操作
Win11查看安装的Python路径及安装的库 Python PEP8 代码规范常见问题及解决方案 Python3操作MySQL8.XX创建表|CRUD基本操作 Python3操作SQLite3创建表主键自增长|CRUD基本操作 anaconda3最新版安装|使用详情|Error: Please select a valid Python interpreter Python函数绘…...

B. Comparison String
题目: 样例: 输入 4 4 <<>> 4 >><< 5 >>>>> 7 <><><><输出 3 3 6 2 思路: 由题意,条件是 又因为要使用尽可能少的数字,这是一道贪心题,所以…...

python端口扫描
扫描所有端口 import socket, threading, os, timedef port_thread(ip, start, step, timeout):for port in range(start, start step):s socket.socket()s.settimeout(timeout)try:s.connect((ip, port))print(f"port[{port}] 可用")except Exception as e:# pri…...

国庆第二天
#include<th.h>#define ERR_MSG(msg) do{\fprintf(stderr,"__%d__",__LINE__);\perror(msg);\ }while(0)#define PORT 6666 #define IP "192.168.2.3"//键盘输入事件 int serverkeyboard(fd_set readfds) {char buf[128] "";int sndfd -…...
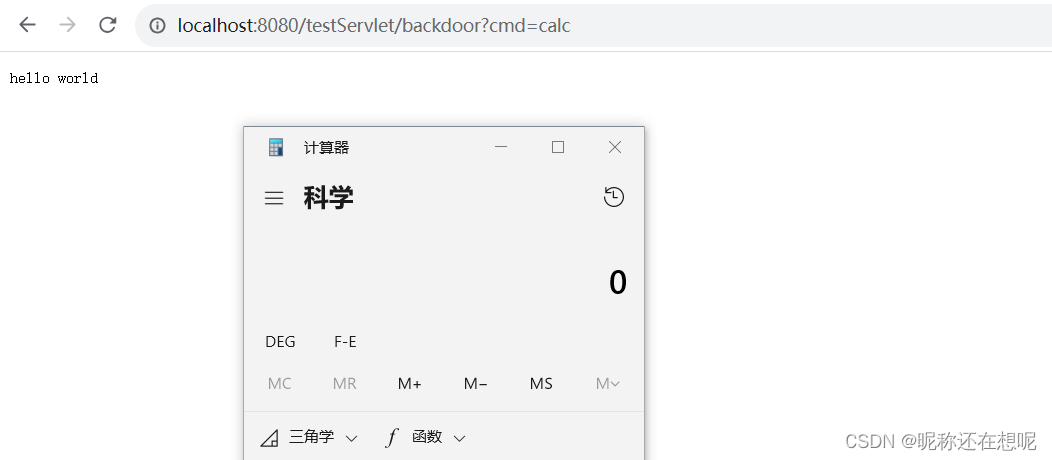
Java安全之servlet内存马分析
目录 前言 什么是中间键 了解jsp的本质 理解servlet运行机制 servlet的生命周期 Tomcat总体架构 查看Context 的源码 servlet内存马实现 参考 前言 php和jsp一句话马我想大家都知道,早先就听小伙伴说过一句话木马已经过时了,现在是内存马的天下…...

2023年第二十届中国研究生数学建模竞赛总结与分享
今天是国庆节,祝祖国繁荣富强。正好也学习不下去,就想着写写博客,总结一下自己在参加2023年第20届中国研究生数学建模比赛的一些感受。 目录 1.基本介绍 2.比赛分享 1.基本介绍 1. 竞赛时间:竞赛定于2023年9月22日8:00至2023年9…...
)
Web前端-Vue2+Vue3基础入门到实战项目-Day1(初始Vue, Vue指令, 小黑记事本)
Web前端-Vue2Vue3基础入门到实战项目-Day1 Vue快速上手创建一个Vue实例插值表达式Vue响应式特性 Vue指令指令初识 和 v-htmlv-show 和 v-ifv-else 和 v-else-ifv-on内联语句methods处理函数调用传参 v-bind案例 - 波仔的学习之旅v-forv-for基本使用案例 - 小黑的书架v-for的key…...
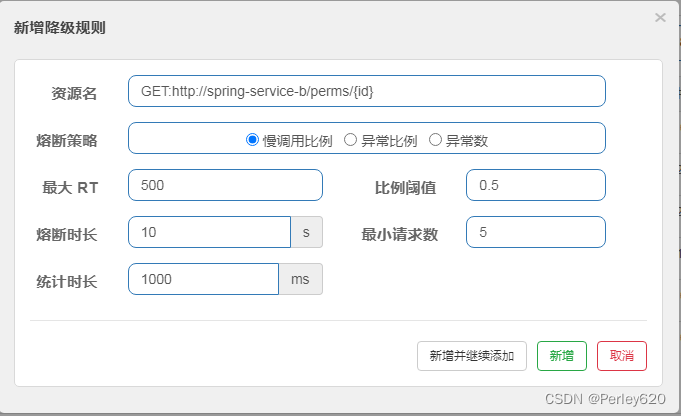
Sentinel学习(2)——sentinel的使用,引入依赖和配置 对消费者进行流控 对生产者进行熔断降级
前言 Sentinel 是面向分布式、多语言异构化服务架构的流量治理组件,主要以流量为切入点,从流量路由、流量控制、流量整形、熔断降级、系统自适应过载保护、热点流量防护等多个维度来帮助开发者保障微服务的稳定性。 本篇博客介绍sentinel的使用&#x…...

springboot 简单配置mongodb多数据源
准备工作: 本地mongodb一个创建两个数据库 student 和 student-two 所需jar包: # springboot基于的版本 <parent><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-parent</artifactId>&l…...
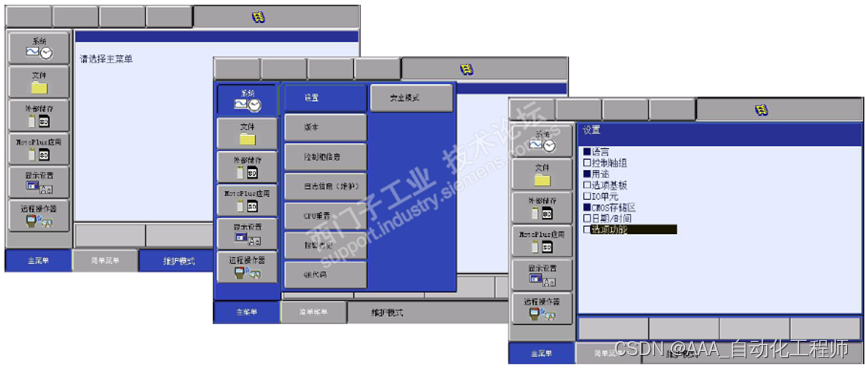
西门子S7-1200使用LRCF通信库与安川机器人进行EthernetIP通信的具体方法示例
西门子S7-1200使用LRCF通信库与安川机器人进行EthernetIP通信的具体方法示例 准备条件: PLC:S7-1200 1214C DC/DC/DC 系统版本4.5及以上。 机器人控制柜:安川YRC1000。 软件:TIA V17 PLC做主站,机器人做从站。 具体方法可参考以下内容: 使用的库文件为西门子 1200系列…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...
