【人工智能导论】线性回归模型
一、线性回归模型概述
线性回归是利用函数对一个或多个自变量和因变量之间关系进行建模的一种回归分析。简单来说,就是试图找到自变量与因变量之间的关系。

二、线性回归案例:房价预测
1、案例分析
问题:现在要预测140平方的房屋的价格,应该怎么做呢?
答案:当然是建立于一个预测模型,根据输入的特征,输出预测值(房价)。
进一步:使用线性回归模型如何呢?
采用线性方程 f ( x ) = m x + b f(x)=mx+b f(x)=mx+b来拟合房价走势。其中,x为房屋的面积,f(x)为模型输出的预测价格。
import itertools
import numpy as np
data = np.array([[80,200],[95,230],[104,245],[112,247],[125,259],[135,262]])#输出的所有组合保存在列表 com_lists中。
com_lists = list(itertools.combinations(data, 2))
对于预测模型 ,发现和获得参数m和b的过程称为模型训练。
# 定义容器列表ms和bs,分别存放不同组合获得的参数 m 和 b。
ms = []
bs = []for comlist in com_lists:x1, y1 = comlist[0]x2, y2 = comlist[1]# 因为有下列等式成立# y1 = m * x1 + b# y2 = m * x2 + b#所以m = (y2 - y1) / (x2 - x1)b = y1 - m * x1 # or b = y2 - m * x2ms.append(m)bs.append(b)m,b = np.mean(ms),np.mean(bs)
print(ms, bs)
print(m,b)
模型的参数m和b使用ms和bs的均值靠谱吗?
依据什么来判断?
一般情况下,评估模型,通常采用均方误差来进行评估。
2、均方误差
均方误差(mean-square error,MSE)是反映估计量与被估计量之间差异程度的一种度量。均方误差是衡量数据偏离真实值的距离,是差值的平方和的平均数。
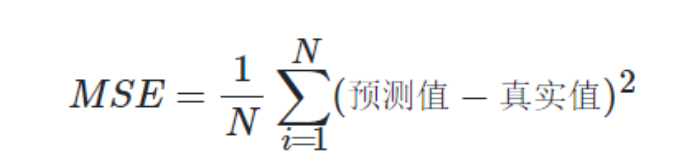
评估预测模型的好坏(m和b参数值是否合适),就是模型 f ( x ) = m x + b f(x)=mx+b f(x)=mx+b 这个预测模型得到的预测结果f(x)与标记值y 接近的程度。
通常,MSE公式前面的1/N 保留和去掉关系不大,也可以将上面的公式简化为:

#计算均方误差
losses = []
for x,y in data:predict = m * x + bloss = (y - predict)**2losses.append(loss)print(losses)
print(np.mean(losses))
3、梯度下降算法
梯度:梯度是一个矢量,在其方向上的方向导数最大,也就是函数在该点处沿着梯度的方向变化最快,变化率最大。
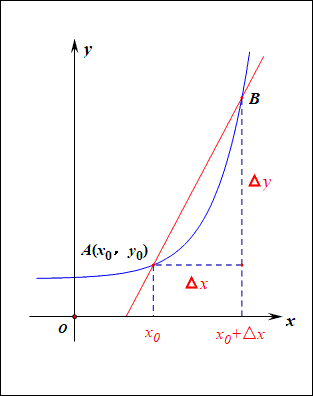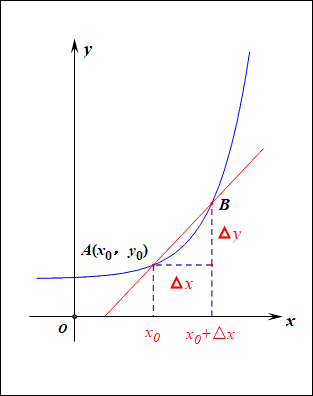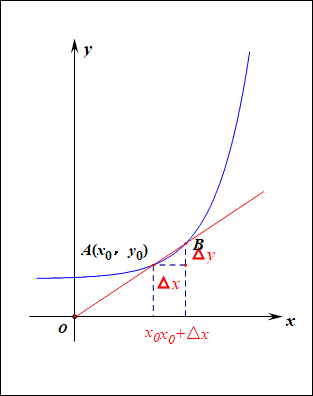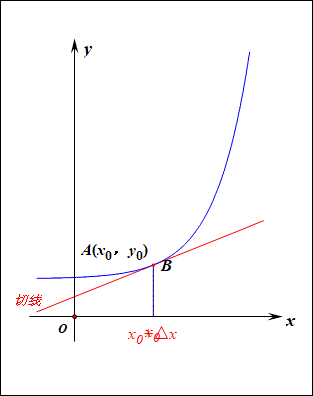
当函数y=f(x)的自变量x在一点x0上产生一个增量Δx时,函数输出值的增量Δy与自变量增量Δx的比值,在Δx趋于0时的极限a如果存在,a即为在x0处的导数,记作发或df(x0)/dx。
导数的本质是通过极限的概念对函数进行局部的线性逼近(目标时获得极值)。
在机器学习中逐步逼近、迭代求解最优化时,经常会使用到梯度,沿着梯度向量的方向是函数增加的最快,容易找最大值。反过来,沿着梯度向量相反的地方,梯度减少的最快,容易找到最小值。
循着这样的思路,获得理想预测模型的目标是使得损失函数(代价函数)更小,而获取极小值,可以采用梯度下降方法。
梯度下降方法:通过计算梯度,一步步迭代求解,不断寻找损失函数的极小值点,以获得最佳的f(x)。
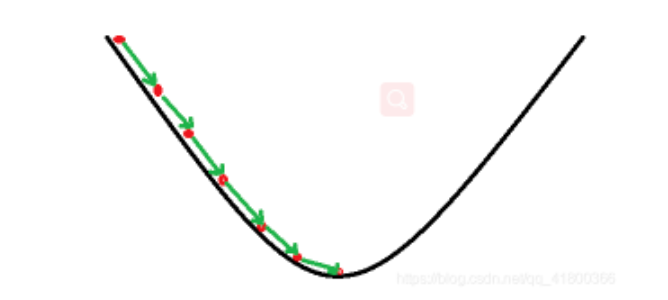
4、梯度下降算法的实现
1、首先,确定模型函数和损失函数(f(x)=mx+b, loss=MSE)
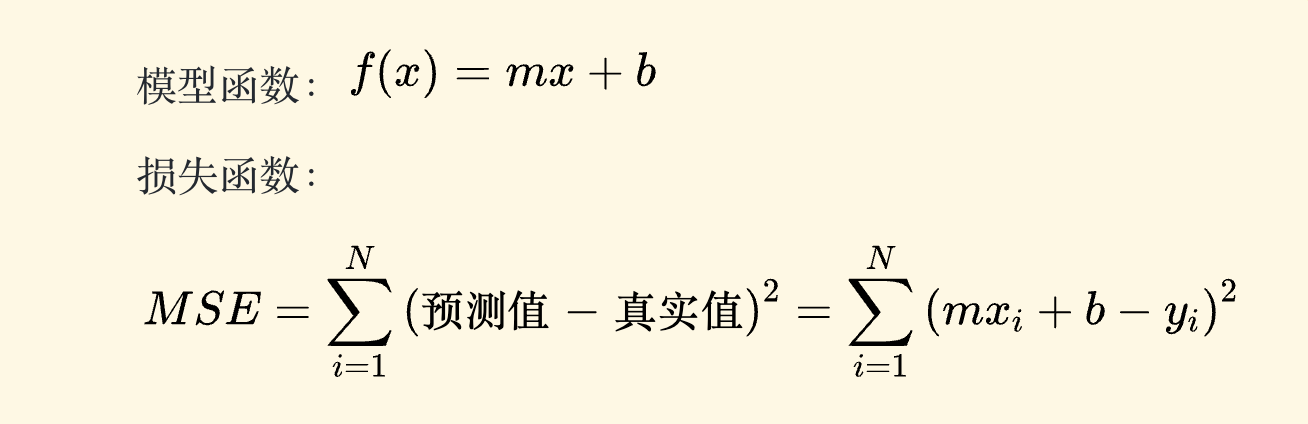
2、设定模型参数初始值和算法终止条件(例如:m,b,lr,epoch)
3、开始迭代
4、计算损失函数的梯度(参数的偏导数)

5、步长乘以梯度,得到当前位置下降的距离,更新参数

6、判断迭代过程是否终止(例如循环迭代次数满足),继续则跳转到3,否则退出。
# 实现梯度下降的算法
# 预测模型: f(x) = mx+b ,用于预测房屋的真实价格import numpy as np
import matplotlib.pyplot as plt
data = np.array([[80,200],[95,230],[104,245],[112,247],[125,259],[135,262]])# 求解f(x) = mx + b ,其中(x,y)来自data,y为标记数据
# 目标:y 与 f(x)之间的差距尽量小# 初始化参数
m = 1
b = 1
lr = 0.00001# 梯度下降的函数
def gradientdecent(m, b, data, lr): # 当前的m,b和数据data,学习率lrloss, mpd, bpd = 0, 0, 0 # loss 为均方误差,mpd为m的偏导数,# bpd为b的偏导数for xi, yi in data:loss += (m * xi + b - yi) ** 2 # 计算msebpd += (m * xi + b - yi) * 2 # 计算loss/b偏导数mpd += (m * xi + b - yi) * 2 * xi # 计算loss/m偏导数# 更新m,bN = len(data)loss = loss / Nmpd = mpd / Nbpd = bpd / Nm = m - mpd * lrb = b - bpd * lrreturn loss, m, b# 训练过程,循环一定的次数,或者符合某种条件后结束
for epoch in range(3000000):mse,m,b = gradientdecent(m,b,data,lr)if epoch%100000 == 0:print(f"loss={mse:.4f},m={m:.4f},b={b:.4f}")
结果是:loss=42.8698,虽然相比之前手工得到的f(x)=mx+b模型的loss=70.89变小了不少,但是仍然无法接近0。这是因为,线性模型无法有效拟合现实世界中真实曲线的变化趋势。
三、利用PyTorch进行梯度计算
1、梯度的自动计算
在多元函数中,某点的梯为偏导数(由每个自变量所对应的偏导数所组成的向量)。如损失函数的 J ( θ , x ) = f θ ( x ) − y J(θ, x) =fθ(x) - y J(θ,x)=fθ(x)−y ,且 θ = [ θ 1 , θ 2 , . . . , . . . , θ k ] θ = [θ_1,θ_2,...,... ,θ_k] θ=[θ1,θ2,...,...,θk]。
对于线性回归模型 f θ ( x ) = m x + b f_θ(x) = mx + b fθ(x)=mx+b, 其中 θ 1 = m θ_1=m θ1=m和 θ 2 = b θ_2=b θ2=b。 f θ ( x ) f_θ(x) fθ(x)的计算过程就是前向传播。
使用梯度下降方法确定模型 f θ ( x ) fθ(x) fθ(x) 中的参数 θ θ θ ,以及参数 θ θ θ 的更新都是在向后传播的过程中完成的。
PyTorch 如何识别这些需要计算梯度的参数?
无需为所有张量计算梯度!
将 模型参数张量 θ θ θ 的 requires_grad属性设置为True,在前向传播过程中,将会在该张量的整个传播链条上,生成计算梯度的函数,并预留保存梯度的存储空间
import torch# 对四个张量自动赋值,并设置某个张量(例如 m1)需要计算偏导数(需要后向传播)
m1 = torch.randn(1, requires_grad=True)
m2 = torch.randn(1, requires_grad=False)
b1 = torch.randn(1)
b2 = torch.randn(1)def forward1(x):global m1, b1return m1 * x + b1def forward2(x):global m2, b2return m2 * x + b2data = [[2, 5]] # m=2 b=1 最佳
x = data[0][0]
y = data[0][1]# 1.前向传播,构建了计算图
predict1 = forward1(x)
predict2 = forward2(x)# 构造损失(代价)函数
loss1 = (y - predict1) ** 2
loss2 = (y - predict2) ** 2# 2.向后传播
loss1.backward()
# loss2.backward() # why?# 查看计算图中是否保留了计算梯度的函数
print(loss1.grad_fn) # 有
print(loss2.grad_fn) # 无# 向后传播发生后, 查看模型参数 m1和m2 是否记录了梯度值
print(m1.grad) # 已记录
print(m2.grad) # loss2 无法进行向后传播,无记录# 手工计算m1的偏导值 mpd1,并与 m1.grad 比较
mpd1 = 2 * (y - (m1 * x + b1)) * (-1 * x)
print(mpd1 == m1.grad)

2、多层神经网络的梯度计算
为了完成更复杂的回归或分类任务,模型的构建会更加复杂(嵌套层次更多,方法嵌套调用)。
对于复杂函数,一个子方法的输出,是另一个子方法的输入。
对应到神经网络模型,一个子方法就是神经网络中的一层。上一层中神经元的输出,是下一层神经元的输入。

前向传播 forward:
y = f ( x ) y=f(x) y=f(x) 、 z = g ( y ) z=g(y) z=g(y)
向后传播 backward:
1、要得到 x 的梯度
2、先从 开始
开始
3、然后
4、最后
# 多层神经网络计算梯度案例# x中的特征数据批量定义,batch=3
x = torch.randn(3, requires_grad=True) # x=[x1,x2,x3]# 第二层定义
y = x + 2# 输出层定义
z = 3 * y ** 2 # z=3y2# 建立J函数,可向后传播(此处J=z.mean(),该函数无实际意义)
z = z.mean() # z=(z1+z2+z3)/3 只有标量可以向后传播# 可以打印并观察x,y,z, 计算梯度的传播链条已经建立# 向后传播, 调用链条中的梯度计算函数(求偏导)
z.backward()# 打印(在向后传播过程中,自动计算得到的) x 的梯度值
print(x.grad)
# 注意,从z开始向后传播, 手工推导可知:dJ/dx= dz/dx = 2*(x+2)
print(2 * (x + 2))
# 比较下,手工计算和自动梯度下降方法得到的值是否相同
很多时候,y 与 z 无需计算梯度。
因此,当确定不会调用Tensor.backward()时,禁用梯度计算将减少原本需要张量在requires_grad=True时的计算的内存消耗。
在with torch.no_grad()的作用域中,所有的张量都不进行梯度计算。
# a要求计算梯度,则吧需要预留资源(偏导函数、梯度占用空间等)
a = torch.randn(2, 2, requires_grad=True)
b = (a ** 2)
print(b.grad_fn)
print(b.requires_grad)# with作用域设置为no_grad,前向传播才不会为其保留偏导传播链
with torch.no_grad():c = (a ** 2)
print(c.grad_fn)
print(c.requires_grad)
3、梯度清空
在PyTorch中,求解张量的梯度的方法是torch.autograd.backward,多次运行该函数,会将计算得到的梯度累加起来。
import torch# 首先定义张量(需要计算梯度)
x = torch.ones(4, requires_grad=True)# 将x作为输入,分别建立两个 复合函数 y 和 z
# 1.第一个复合函数
y = (2 * x + 1).sum() # 问题:为什么要sum()???
# 2.第二个复合函数
z = (2 * x).sum()# 调用 y 和 z 的向后传播(自动计算梯度)#不是J的向后传播都是耍流氓!
y.backward()
print("dy/dx偏导数:", x.grad)
z.backward()
print("dz/dx偏导数:", x.grad)

根据上面的结果,可知如果对张量y和z分别求x的梯度,关于x的偏导会累加到 x.grad 中。
为了避免累加,通常计算梯度后,先清空梯度,再进行其他张量的梯度计算。PyTorch中,使用 grad.zero_() 清空梯度。
import torchx = torch.ones(4, requires_grad=True)
y = (2 * x + 1).sum()
z = (2 * x).sum()y.backward()
print("第一次偏导:", x.grad)x.grad.zero_()
z.backward()
print("第二次偏导:",x.grad)

神经网络模型在训练时,需要循环迭代来更新参数。
如果求出的梯度,一直叠加,就会导致结果没有意义。因此需要对张量的偏导进行清空。
此外,优化器也提供了类似清空梯度的函数:zero_grad()。
optimizer = torch.optim.SGD([x], lr=0.1)
# 更新参数,自动调用向后传播,并自动更新模型的参数
optimizer.step()
optimizer.zero_grad()
print(optimizer)
4、正向和向后传播的函数定义
神经网络本质上是一个非常复杂且有大量参数的复合函数(函数链条)。
1)前向传播
在PyTorch中,前向传播就是通过函数的定义来构建计算图(传播链条),形成神经网络的基本框架,并得到神经网络的输出(预测值)。
例如, y = ( a + b ) ∗ ( b + c ) y = (a+b)*(b+c) y=(a+b)∗(b+c)。PyTorch 利用 forward函数的定义,实现了“计算图”的构建。
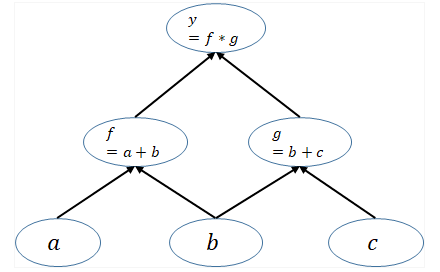
2)向后传播
根据计算图,在向后传播过程,通过计算参数 w 的梯度,并不断迭代更新参数 w,目标是使 J(代价)函数获得最小值。
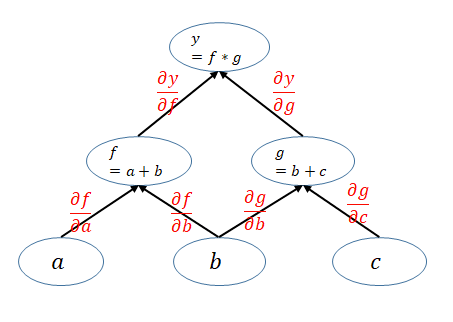
前向传播算法定义神经网络(计算图),初始参数为随机数(一次性)
向后传播算法优化迭代更新模型的参数值(多次),获得最优模型
3)前向传播函数的定义
以线性回归模型 f ( x ) = m x + b f(x)=mx+b f(x)=mx+b,其中 b=0为例。该函数的输入数据为x, 参数为w, 评估模型使用loss=MSE。
import torch
# 定义测试数据
x = torch.tensor(1.) # 输入特征
y = torch.tensor(2.) # 标记值
w = torch.tensor(1.,requires_grad=True) # 模型参数值,随机赋值1# 正向传播 : f(x) = wx
# 模型的定义,根据 x,y 值可知参数 w = 2
def forward(x,w): # 计算预测值 pred,并返回pred = w*xreturn pred# 调用正向传播
predict = forward(x,w)
print(predict)
初始值可以是任意值
4)向后传播函数的定义
实践中,预测模型的最佳参数不会这样容易得知。
通常需要多次迭代(训练),使用梯度下降方法计算模型参数的梯度,并更新模型参数,使损失函数取值最小,因此在向后传播过程中,模型参数将会不断逼近最优值,直到终止训练。
在本例中,模型参数 w 开始时被随机赋值为 1。在向后传播过程中,模型参数 w 将从 1 迭代更新为(接近) 2 ,该过程就是模型的训练过程。
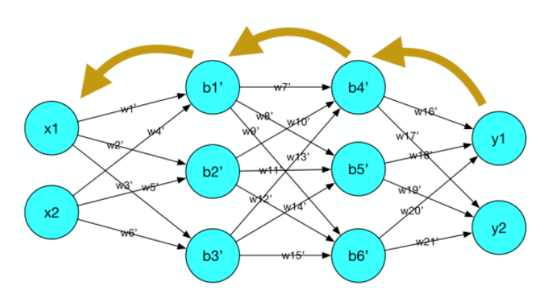
在PyTorch中,如果计算损失函数的计算结果为张量 loss(维度为0的张量),则调用 **loss.backward()**向后传播,PyTorch将自动为模型参数计算梯度值。
# 预测模型:f(x)=wx
# 输入特征数据、标记值:x,y (可观察)
# 模型参数:w(赋随机值1)
# 预测值已得到: predict = forward(x,w)loss = (predict - y)**2 # MSE = (预测值 - 真实值)的平方
loss.backward()print("此时,loss关于w的偏导值:", w.grad)
5、模型训练的问题与优化
训练模型的过程,就是不断迭代,在向后传播过程中,不断采用梯度下降方法计算模型参数的梯度方向,并沿着该方向不断迭代,以修正模型的参数,目标是使得损失函数结果为最小,这个过程就是寻找最优参数值的过程。
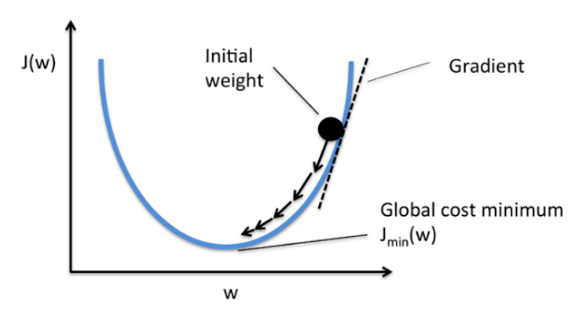
模型训练过程包括以下步骤:
- 正向传播
- 计算损失
- 向后传播
- 更新参数
- 清空梯度
import torch# 模型为: f(x)=wx
# 定义测试数据(与之前的数据不同,为成批数据,batch=4)可pycharm调试观察
X = torch.tensor([1,2,3,4],dtype=torch.float32)
Y = torch.tensor([2,4,6,8],dtype=torch.float32)
W = torch.tensor(0,dtype=torch.float32,requires_grad=True)
# 1.正向传播
def forward(w,x): #构建计算图return x*w# 2.计算损失
def lossFunction(y_pred,y): #确定损失函数return ((y_pred - y)**2).mean() #成批计算,从X和Y的定义也可以看出# 模型训练过程
learning_rate = 0.01
for epoch in range(100): # epoch为训练的次数# 1.正向传播pred = forward(W, X)# 2.计算损失loss = lossFunction(pred, Y)# 3.向后传播loss.backward()# 4.更新参数W.data = W.data - learning_rate * W.grad# 5.清空梯度W.grad.zero_()if epoch%10 == 0:print(f"loss={loss.item()},w={W.item()}")6、使用PyTorch进行模型训练
1)PyTorch中的常用损失函数
(1)均方差损失函数(MSELoss)
计算预测值(Predict) 和标记值 (Label) 之差的均方差。
torch.nn.MSELoss()
(2) 交叉熵损失 (CrossEntropyLoss)
在多分类任务中,交叉熵描述了预测分类和标记间不同概率分布的差异。
torch.nn.CrossEntropyLoss()
(3) 二进制交叉熵损失(BCELoss)
二分类任务时的交叉熵计算函数。
torch.nn.BCELoss()
import torch
import torch.nn as nn# 初始化数据集
X = torch.tensor([1,2,3,4],dtype=torch.float32)
Y = torch.tensor([2,4,6,8],dtype=torch.float32)
w = torch.tensor(0.0, dtype=torch.float32, requires_grad=True)def forward(x):return w*x# 测试代码
pre = forward(X)
print(pre)# 均方差计算预测值和真实值之间的距离
loss = torch.nn.MSELoss()# 计算此时的损失
y_pre = forward(X)
l = loss(y_pre,Y)
print(f"此时的损失:{l}")
2)优化器
优化器的目标就是:根据损失函数,找到更新参数的最优方法或路径。
随机梯度下降法(stochastic gradient descent,SGD)
optimizer = torch.optim.SGD([W], lr=learning_rate) #定义
# 第一个参数张量 [W] 为模型中要更新的参数
# 第二个lr 为学习率(步长)optimizer.step() # 根据参数梯度,对模型中的参数进行更新。
optimizer.zero_grad() # 清空模型参数梯度,防止累计情况发生
优化器可一次性对所有模型参数变量进行更新,免去手动更新参数的繁琐(Impossible Mission不可能完成的任务)。
import torch
import torch.nn as nn# 初始化数据集
X = torch.tensor([1,2,3,4],dtype=torch.float32)
Y = torch.tensor([2,4,6,8],dtype=torch.float32)
w = torch.tensor(0.0, dtype=torch.float32, requires_grad=True)def forward(x):return w*x# 均方差计算预测值和真实值之间的距离
loss = torch.nn.MSELoss()# 首先,定义损失函数和优化器
learning_rate = 0.01
n_iters = 100
loss = nn.MSELoss()
optimizer = torch.optim.SGD([w], lr=learning_rate)
print(optimizer)
# 然后, 根据正向传播结果, 更新梯度,进而更新权重值
# 开始模型训练
for epoch in range(n_iters):# 1.正向传播y_pre = forward(X)# 2.计算损失l = loss(Y, y_pre)# 3.向后传播(计算梯度)l.backward()# 4.更新权重,即向梯度反方向走一步,由优化器完成optimizer.step()# 5.清空梯度,由优化器完成optimizer.zero_grad()if epoch % 10 == 0:print(f"epoch:{epoch}, w={w},loss={l:.8f}")
3)模型定义
基于Pytorch,构建神经网络,并进行训练的代码步骤如下(特征数据X,标记数据Y)
- 定义模型(确定模型对象与模型参数,构建计算图(传播链))
- 定义损失(代价)函数loss
- 定义优化器optimizer,利用其优化模型参数
- 通过model(X) 调用forward,前向传播
- 利用loss(Y, y_pre)计算模型的损失
- 利用loss.backward() 向后传播,计算模型参数的梯度
- 利用optimizer.step() 更新模型参数的权重
- 利用optimizer.zero_grad() 清空模型参数的梯度
- 重复4-8的操作,进行训练直到达到预定结束条件
使用PyTorch可以极大的简化我们编程的难度。
通常只需要改变模型、损失函数和优化器的定义形式,就能快速搭建神经网络模型,进行训练以解决不同的深度学习问题。
四、利用PyTorch定义神经网络模型类
在PyTorch中,自定义神经网络类,通常继承于nn.Module类,并对子类的构造函数(init)和前向传播函数(forward)进行重新实现。
1、利用sklearn生成模拟数据
import numpy as np
from sklearn import datasets
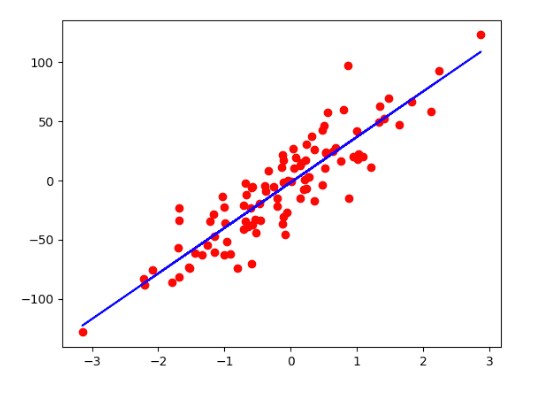
import matplotlib.pyplot as pltX_numpy,Y_numpy = datasets.make_regression(n_samples=100,n_features=1,noise=20,random_state=12
)plt.plot(X_numpy,Y_numpy,"ro") # 红色圆点
plt.show()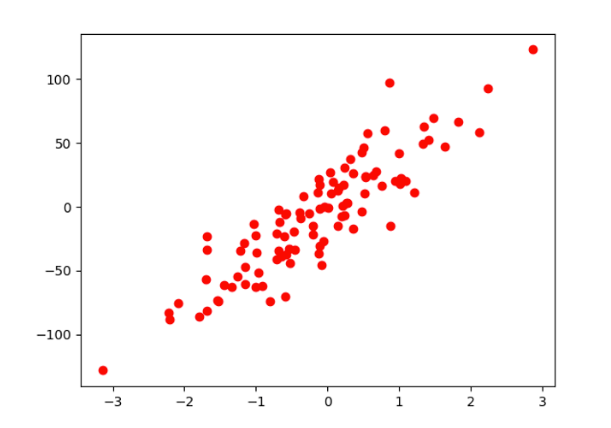
将数据集转成PyTorch使用的张量形式。
import torch
# 将numpy 的数据类型转成tensor
X = torch.from_numpy(X_numpy.astype(np.float32))
Y = torch.from_numpy(Y_numpy.astype(np.float32))print(X.shape,Y.shape)
# 对Y进行格式统一
Y = Y.view(100,1)
# 模型训练
print(X.shape,Y.shape)
2、 神经网络类的定义
线性函数模型的定义和训练:
# 1. 定义模型(包括正向传播方法forward)
n_samples,in_features = X.shape
n_labels, out_features = Y.shape# 搭建自己的神经网络,并创建模型对象
class MyModel(torch.nn.Module):# 初始化函数的定义,定义神经网络和参数def __init__(self, in_features_len, out_features_len):super(MyModel, self).__init__()# 构建线性层self.linear = torch.nn.Linear(in_features_len, out_features_len)# 向前传播,构建计算图def forward(self, x):"""重写了父类的forward函数,正向传播"""out = self.linear(x)return outmodel = MyModel(in_features,out_features)# 2.定义损失(代价)函数loss
lossF = torch.nn.MSELoss()# 3. 定义优化器optimizer,利用其管理模型参数
optimizer = torch.optim.SGD(model.parameters(),lr=0.1)
print(list(model.parameters()))# 模型训练
n_iters = 100
for epoch in range(n_iters):# 4. 通过model(X) 调用forward,进行前向传播pred = model(X)# 5. 利用loss(Y, y_pre)计算模型的损失l = lossF(Y,pred)#6. 利用loss.backward() 进行向后传播,计算模型的梯度l.backward()# 7. 利用optimizer.step() 更新权重optimizer.step()# 8. 利用optimizer.zero_grad() 清空梯度optimizer.zero_grad()# 打印结果if epoch%10 == 0:w,b = model.parameters()# print(f"epoch:{epoch},w={w[0][0].item()}")print(f"loss={l.item():.8f},w={w.item():.4f},b = {b.item()}")with torch.no_grad():predicted = model(X).numpy()plt.plot(X_numpy,Y_numpy,"ro")
plt.plot(X_numpy,predicted,"b")
plt.show()
相关文章:

【人工智能导论】线性回归模型
一、线性回归模型概述 线性回归是利用函数对一个或多个自变量和因变量之间关系进行建模的一种回归分析。简单来说,就是试图找到自变量与因变量之间的关系。 二、线性回归案例:房价预测 1、案例分析 问题:现在要预测140平方的房屋的价格&…...
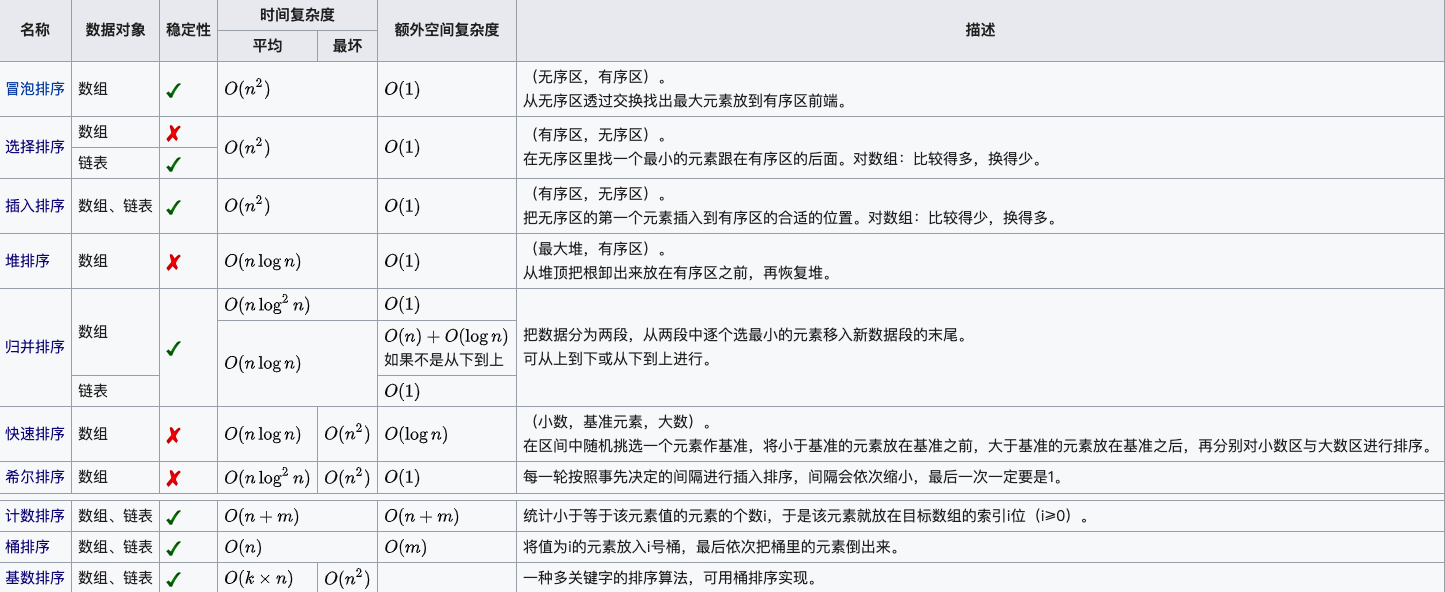
十大常见排序算法详解(附Java代码实现和代码解析)
文章目录 十大排序算法⛅前言🌱1、排序概述🌴2、排序的实现🌵2.1 插入排序🐳2.1.1 直接插入排序算法介绍算法实现 🐳2.1.2 希尔排序算法介绍算法实现 🌵2.2 选择排序🐳2.2.1 选择排序算法介绍算…...
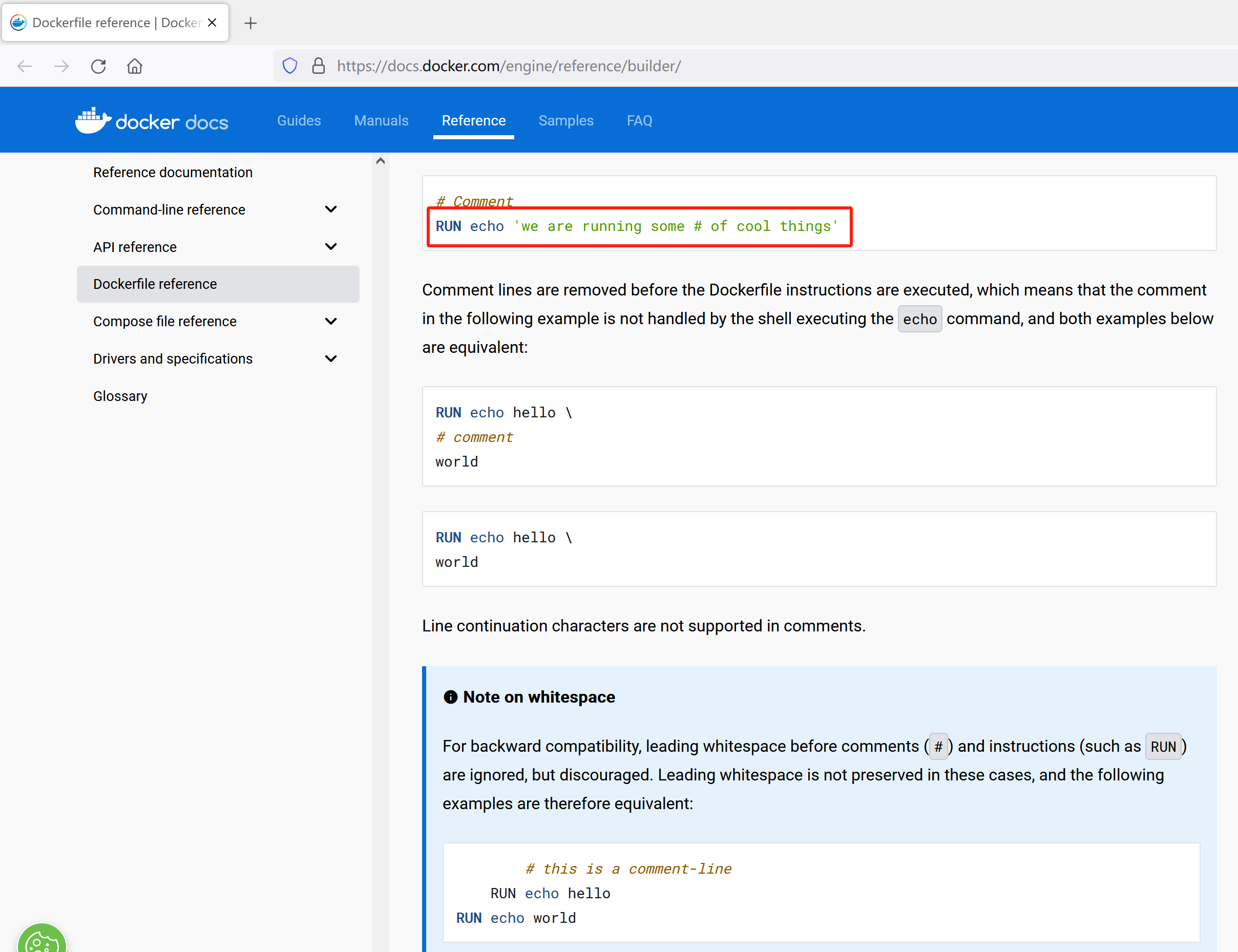
在Ubuntu上通过Portainer部署微服务项目
这篇文章主要记录自己在ubuntu上部署自己的微服务应用的过程,文章中使用了docker、docker-compose和portainer,在部署过程中遇到了不少问题,因为博主也是初学docker-compose,通过这次部署实战确实有所收获,在这篇文章一…...
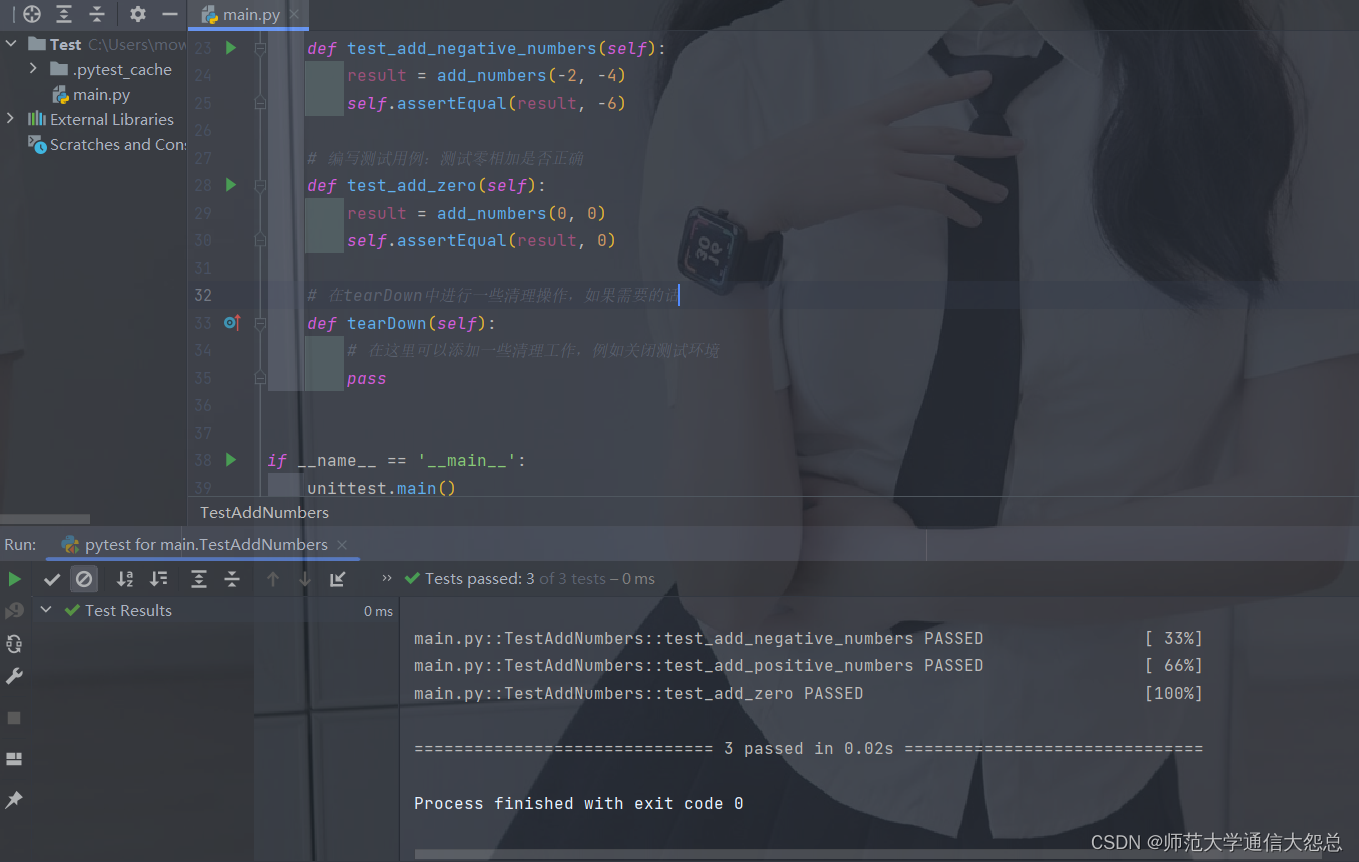
软件测试基础学习
注意: 各位同学们,今年本人求职目前遇到的情况大体是这样了,开发太卷,学历高的话优势非常的大,公司会根据实际情况考虑是否值得培养(哪怕技术差一点);学历稍微低一些但是技术熟练的…...

移动手机截图,读取图片尺寸
这个代码的设计初衷是为了解决图片处理过程中的一些痛点。想象一下,我们都曾遇到过这样的情况:相机拍摄出来的照片、网络下载的图片,尺寸五花八门,大小不一。而我们又渴望将它们整理成一套拥有统一尺寸的图片,让它们更…...

服务器应用程序不可用的原因是什么引起的
服务器应用程序不可用的原因是什么引起的 服务器应用程序不可用的原因是什么引起的?其实服务器应用程序不可用可能是由多种原因引起的。主要包括软件故障、网络问题、硬件故障、安全问题、配置错误、容量不足、数据库问题等,具体详细服务器应用程序不可用的原因如下…...

使用SPY++查看窗口信息去排查客户端UI软件问题
目录 1、使用SPY++查看窗口的信息 2、使用SPY++查看某些软件UI窗口用什么UI组件实现的...
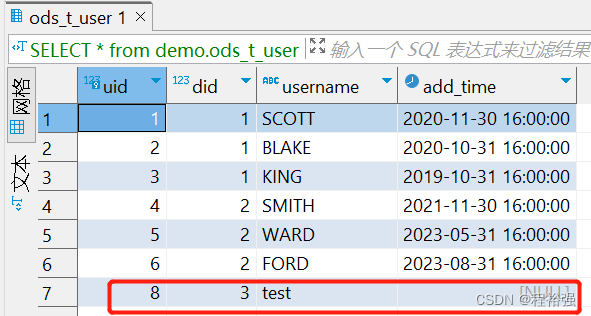
Flink CDC MySQL同步MySQL错误记录
1、启动 Flink SQL [appuserwhtpjfscpt01 flink-1.17.1]$ bin/sql-client.sh2、新建源表 问题1:Encountered “(” 处理方法:去掉int(11),改为int Flink SQL> CREATE TABLE t_user ( > uid int(11) NOT NULL AUTO_INCREMENT COMME…...
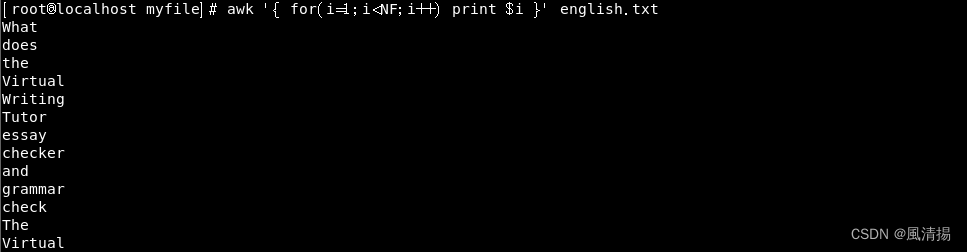
深入了解 Linux 中的 AWK 命令:文本处理的瑞士军刀
简介 在Linux和Unix操作系统中,文本处理是一个常见的任务。AWK命令是一个强大的文本处理工具,专门进行文本截取和分析,它允许你在文本文件中查找、过滤、处理和格式化数据。本文将深入介绍Linux中的AWK命令,让你了解其基本用法和…...

【RuoYi项目分析】网关的AuthFilter完成“认证”,注意是认证而不是权限
文章目录 1. 功能介绍2. AuthFilter的配置3. AuthFilter实现分析4. 资料参考 过滤器的功能是检验经过网关的每一个请求,检查 token 中的信息是否有效。 注意是“认证检查”,而不是“权限” 1. 功能介绍 1、在用户完成登录后,程序会把用户相关…...

excel将文件夹下面的表格文件指定名称的sheet批量导出到指定文件中,并按照文件名保存在新文件的不同sheet中
excel将文件夹下面的表格文件指定名称的sheet批量导出到指定文件中,并按照文件名保存在新文件的不同sheet中 import pandas as pd import ositems os.listdir("./") sheetname"" for item in items:if item.__contains__(xls):dfpd.read_exc…...
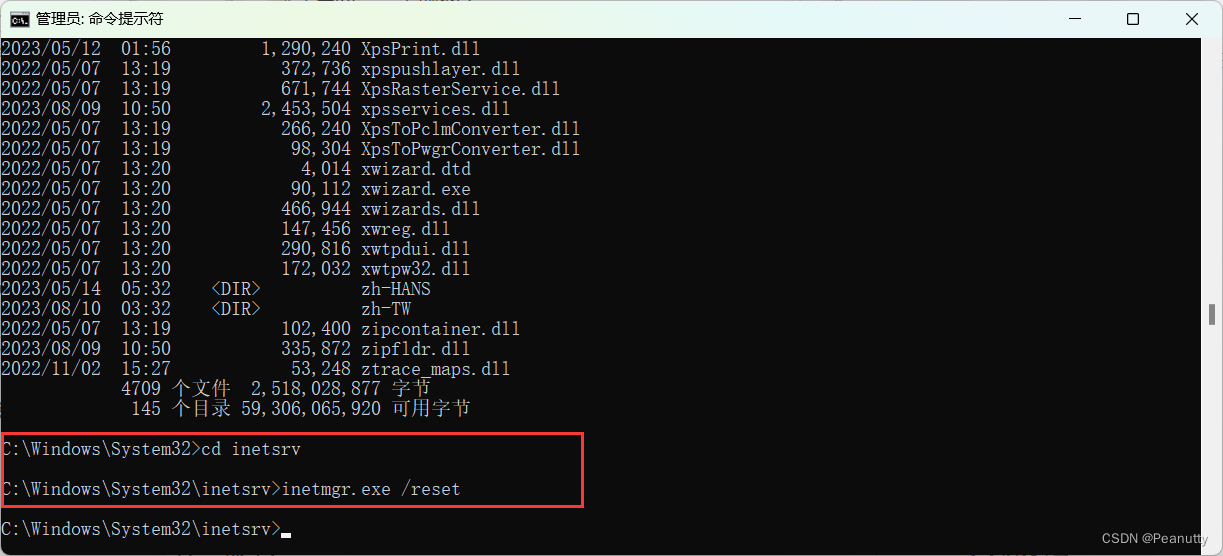
IIS管理器无法打开。启动后,在任务栏中有,但是窗口不见了
找到IIS管理器启动程序的所在位置 并在cmd命令行中调用 inetmgr.exe /reset 进行重启 先查看IIS管理器属性,找到其位置 管理员模式打开cmd命令行,并切换到上面的文件夹下运行Inetmgr.exe /reset 运行完成后可以重新看到IIS窗口 原因:由于某…...
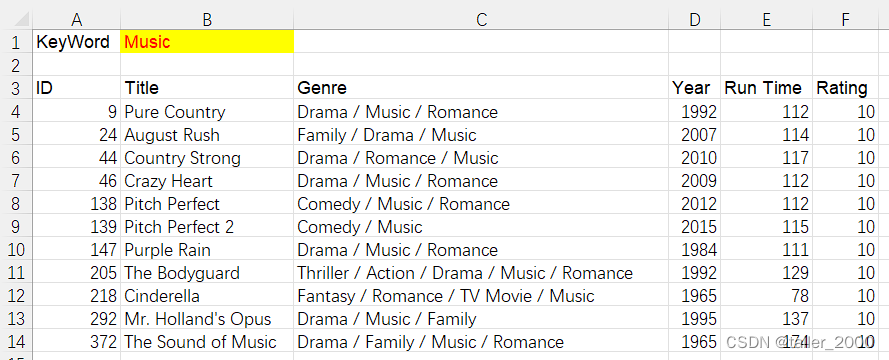
使用VBA实现快速模糊查询数据
实例需求:基础数据保存在Database工作表中,如下图所示。 基础数据有37个字段,上图仅展示部分字段内容,下图中黄色字段为需要提取的数据字段。 在Search工作表B1单元格输入查询关键字Title和Genre字段中搜索关键字,包…...

spring boot flowable多人前加签
1、前加签插件 package com.xxx.flowable.cmd;import com.xxx.auth.security.user.SecurityUser; import com.xxx.commons.ApplicationContextHolder; import com.google.common.collect.Lists; import org.apache.commons.collections.CollectionUtils; import org.apache.co…...

结构体运算符重载
1.降序 struct Point{int x, y;//重载比较符bool operator < (const Point &a) const{return x > a.x;//当前元素大时,是降序} };2.升序 struct Point{int x, y;//重载比较符 // bool operator < (const Point &a) const{ // return x…...

幽默直观的文档作者注释
注释是程序中非常重要的一部分,在不同的编程语言中,注释的风格和语言描述会有所不同。以下是一些常用的注释风格和语言描述: 直观注释:这种注释使用简洁、明了的语言,帮助读者快速地理解代码。例如,代码中…...

前端开发网站推荐
每个人都会遇见那么一个人,永远无法忘却,也永远不能拥有。 以下是一些可以用来查找和比较前端框架的推荐网站: JavaScript框架比较: 这些网站提供了对不同JavaScript框架和库的详细比较和评估。 JavaScripting: 提供了大量的JavaS…...
)
【C语言】通讯录管理系统(保姆级教程+内含源码)
C系列文章目录 目录 C系列文章目录 前言 一,模块化编程 二,系统框架构建 1.成员信息的创建 2.菜单实现 3.系统功能声明 三、系统功能实现 1.初始化通讯录 2.增加联系人 3.显示所有联系人 4.根据姓名查找位置 5.删除指定联系人 6.查找指定联…...

python自动解析301、302重定向链接
嗨喽~大家好呀,这里是魔王呐 ❤ ~! python更多源码/资料/解答/教程等 点击此处跳转文末名片免费获取 使用模块requests 方式代码如下: import requests url_string"http://******" r requests.head(url_string, streamTrue) print r.h…...

【未解决问题】opencv 交叉编译 ffmpeg选项始终为NO
opencv 打不开视频的原因 在交叉编译时候,发现在 pc 端能用 opencv 打开的视频,但是在 rv1126 上打不开。在网上查了很久,原因可能是 ffmpeg 造成的。 解决opencv源代码编译找不到ffmpeg-CSDN博客 交叉编译 ffmpeg 尝试了一天还是第二个博客…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

MySQL 部分重点知识篇
一、数据库对象 1. 主键 定义 :主键是用于唯一标识表中每一行记录的字段或字段组合。它具有唯一性和非空性特点。 作用 :确保数据的完整性,便于数据的查询和管理。 示例 :在学生信息表中,学号可以作为主键ÿ…...

django blank 与 null的区别
1.blank blank控制表单验证时是否允许字段为空 2.null null控制数据库层面是否为空 但是,要注意以下几点: Django的表单验证与null无关:null参数控制的是数据库层面字段是否可以为NULL,而blank参数控制的是Django表单验证时字…...

Sklearn 机器学习 缺失值处理 获取填充失值的统计值
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 使用 Scikit-learn 处理缺失值并提取填充统计信息的完整指南 在机器学习项目中,数据清…...
0609)
书籍“之“字形打印矩阵(8)0609
题目 给定一个矩阵matrix,按照"之"字形的方式打印这个矩阵,例如: 1 2 3 4 5 6 7 8 9 10 11 12 ”之“字形打印的结果为:1,…...