2023湖南省赛游记/题解
省赛拖了大哥们的后腿,感觉随便补个正常一队水平的人,我们一队肯定能AK。只能说自己真的菜,全程帮不上什么忙,还负贡献,真的想笑
B
暴力sg
#include <bits/stdc++.h>
#define ll long long
#define ull unsigned long long
constexpr int N=1e6;
int sg[N+5];
int vis[N+5];
void getsg(){for (int i=1;i<=N;i++){// vis[sg[i-1]]=i;int res=sqrt(1.0*i);if (i==res*res){for (int k=1;k<=res;k++){vis[sg[i-(i-res*res+k*res)]]=i;}}else{for (int k=0;k<=res;k++){vis[sg[i-(i-res*res+k*res)]]=i;}}while (vis[sg[i]]==i){sg[i]++;}}
}
void yrzr(){getsg();int n;std::cin>>n;int sum=0;for (int i=1;i<=n;i++){int x;std::cin>>x;sum^=sg[x];}if (sum){std::cout<<"First\n";}else{std::cout<<"Second\n";}
}
D
大哥赛后说是HN省选dp原题(见状压dp P3188 [HNOI2007] 梦幻岛宝珠),然后这个题比那个题范围还要大,看完题解发现是贪心题,但是还是按位分组的思想去解决问题
首先对于一个目标物品来说,它的需求可以表示为几个二进制位的组合,然后我们分解每一个目标物品到位上,然后将其按位合并,最后可以表示为一个二进制串(用数组表示)
然后对于每一件物品,重量小的物品可以合并成大物品,但大物品不能拆解成小物品,所以我们按位从小到大枚举目标物品数组,贪心地用小物品去满足当前位的数量,然后将剩下的物品贪心地两两合并成下一位的物品。
简要的说就是:目标物品总体可以表示为一个数组,然后拥有的物品贪心从小到大去填补目标重量
#include <bits/stdc++.h>
#define ll long long
#define ull unsigned long long
constexpr int inf=1e9;
std::priority_queue<int,std::vector<int>,std::greater<int>> q[5105];
void yrzr(){int n;std::cin>>n;for (int i=1;i<=n;i++){int x,y;std::cin>>x>>y;q[x].push(y);}int m;std::cin>>m;std::vector<int> sum(5105);while (m--){int t,h;std::cin>>t>>h;while (h){if (h&1) sum[t]++;h>>=1;t++;}}for (int i=0;i<=5100;i++){if (sum[i]>=2){int temp=sum[i],p=i;sum[i]=0;while (temp){if (temp&1) sum[p]++;temp>>=1;p++;}}}int ans=0;for (int i=0;i<=5100;i++){if (q[i].size()<sum[i]){std::cout<<"-1\n";return;}for (int j=1;j<=sum[i];j++){ans+=q[i].top();q[i].pop();}while (q[i].size()>=2){int temp=q[i].top();q[i].pop();temp+=q[i].top();q[i].pop();q[i+1].push(temp);}}std::cout<<ans;
}
F
图论题,首先Floyed求出一个字母变成另一个字母的最小花费,然后对于两个不同的字母,暴力预处理出他们变成同样字母的最小花费。最后A串不动,枚举B串位置,求最小即可
可能有重边,输入时 d i s dis dis取最小
#include <bits/stdc++.h>
#define int long long
#define ull unsigned long long
constexpr int inf=1e16;
void yrzr(){int n,m;std::cin>>n>>m;std::vector<int> a(n),b(n);for (int i=0;i<n;i++){std::cin>>a[i];}for (int i=0;i<n;i++){std::cin>>b[i];}std::vector<std::vector<int>> dis(405,std::vector<int>(405,inf)),c(405,std::vector<int>(405,inf));for (int i=1;i<=m;i++){int x,y,z;std::cin>>x>>y>>z;dis[x][y]=std::min(dis[x][y],z);}for (int i=1;i<=400;i++){dis[i][i]=c[i][i]=0;}for (int k=1;k<=400;k++){for (int i=1;i<=400;i++){for (int j=1;j<=400;j++){dis[i][j]=std::min(dis[i][j],dis[i][k]+dis[k][j]);}}}for (int i=1;i<=400;i++){for (int j=1;j<=400;j++){for (int k=1;k<=400;k++){c[i][j]=std::min(c[i][j],dis[i][k]+dis[j][k]);}}}int ans=inf;for (int i=0;i<n;i++){int sum=0;bool ok=1;for (int j=0;j<n;j++){if (c[a[j]][b[(j+i)%n]]==inf){ok=0;break;}else{sum+=c[a[j]][b[(j+i)%n]];}}if (ok){ans=std::min(ans,sum);}}if (ans==inf){std::cout<<"-1\n";}else{std::cout<<ans<<"\n";}
}
I
数位dp,不知道省赛脑子犯了什么抽,受前几天一道数位dp,直接把状态数组压入map暴力记忆化的影响,想当然的觉得这题也是这么做,大哥直接提出时间复杂度是不够的。后面大哥们说是数位dp加个容斥。
补题的时候也一直在想数位dp+容斥,发现自己容斥不出来(容斥见识的得太少了),看了题解后发现只要一个数位dp就可以了
突然发现这题的思想其实跟前几天做的数位dp是一样的,甚至状态更简单,我们最重要的状态其实就只有当前位第几位,然后还要知道现在有多少个不同的数,这就足够了。因为对于这10个数字来说,后面的数字它只有两种身份,之前选了/没选,所以当前位相同,之前不同的数字个数相同,剩下的方案数就相同,就可以用记忆化。(赛时真的蠢傻了,这种套路思想学数位dp的时候见过很多了)
#include <bits/stdc++.h>
#define ll long long
#define ull unsigned long long
constexpr ll mod=1e9+7;
ll f[200005][12][2][2];
int now[12];
void yrzr(){int n;std::cin>>n;std::vector<int> a(n+1),b(n+1);for (int i=1;i<=n;i++){char ch;std::cin>>ch;a[i]=ch-'0';}for (int i=1;i<=n;i++){char ch;std::cin>>ch;b[i]=ch-'0';}reverse(a.begin()+1,a.end());reverse(b.begin()+1,b.end());int A;std::cin>>A;std::function<ll(int,int,int,int)> dfs=[&](int len,int sum,int dif1,int dif2){if (len==0){return 1LL*(sum==A);}if (sum>A){return 0LL;}if (dif1&&dif2&&f[len][sum][dif1][dif2]){return f[len][sum][dif1][dif2];}int x=(dif1?0:a[len]),y=(dif2?9:b[len]);ll res=0;for (int i=x;i<=y;i++){if (now[i]){now[i]++;res=(res+dfs(len-1,sum,dif1|(a[len]!=i),dif2|(b[len]!=i)))%mod;now[i]--;}else{now[i]++;res=(res+dfs(len-1,sum+1,dif1|(a[len]!=i),dif2|(b[len]!=i)))%mod;now[i]--;}}if (dif1&&dif2) f[len][sum][dif1][dif2]=res;return res;};std::cout<<dfs(n,0,0,0);}
J
分别枚举圆心在三个坐标轴,然后二分圆的半径,接下来考虑怎么check,对于一个点来说,我们去计算出它在球内时,圆心所在的区间,存下区间左右端点和权值(表示是左端点还是右端点),遍历一遍看是否有点满足题意即可
#include <bits/stdc++.h>
#define ll long long
#define ull unsigned long long
constexpr int N=1e5+5;
int n;
ll x[N],y[N],z[N];
struct node{double pos;int val;
}a[N<<1];
bool check(double r){int cnt=0;for (int i=1;i<=n;i++){double res=r*r-y[i]*y[i]-z[i]*z[i];if (res<0) continue;res=sqrt(res);a[++cnt]={x[i]-res,1};a[++cnt]={x[i]+res,-1};}std::sort(a+1,a+1+cnt,[&](node i,node j){return i.pos<j.pos;});int sum=0;for (int i=1;i<=cnt;i++){sum+=a[i].val;if (sum>=n/2){return 1;}}cnt=0;for (int i=1;i<=n;i++){double res=r*r-x[i]*x[i]-z[i]*z[i];if (res<0) continue;res=sqrt(res);a[++cnt]={y[i]-res,1};a[++cnt]={y[i]+res,-1};}std::sort(a+1,a+1+cnt,[&](node i,node j){return i.pos<j.pos;});sum=0;for (int i=1;i<=cnt;i++){sum+=a[i].val;if (sum>=n/2){return 1;}}cnt=0;for (int i=1;i<=n;i++){double res=r*r-x[i]*x[i]-y[i]*y[i];if (res<0) continue;res=sqrt(res);a[++cnt]={z[i]-res,1};a[++cnt]={z[i]+res,-1};}std::sort(a+1,a+1+cnt,[&](node i,node j){return i.pos<j.pos;});sum=0;for (int i=1;i<=cnt;i++){sum+=a[i].val;if (sum>=n/2){return 1;}}return 0;
}
void yrzr(){std::cin>>n;for (int i=1;i<=n;i++){std::cin>>x[i]>>y[i]>>z[i];}double l=0,r=1e6;for (int i=0;i<=50;i++){double mid=(l+r)/2;if (check(mid)){r=mid;}else{l=mid;}}std::cout<<std::fixed<<std::setprecision(7)<<l;
}
K
补的时候相成状压了,然后状压+矩阵加速???,发现不会写
然后看了题解知道是容斥了,所以以后对于这种小数据除了状压也有可能是容斥
想到容斥就很好做了,每次直接暴力二进制枚举哪些城市不去,在转移的矩阵和答案矩阵上去掉那些转移点,然后dp矩阵加速即可
#include <bits/stdc++.h>
#define ll long long
#define ull unsigned long long
constexpr ll mod=1e9+9;
constexpr int N=25;
struct Matrix{int lenn,lenm;ll a[N][N];Matrix() {memset(a,0,sizeof(a));}Matrix operator*(const Matrix &b)const{if (lenm==b.lenn){Matrix res;res.lenn=lenn;res.lenm=b.lenm;for (int i=1;i<=lenn;i++){for (int j=1;j<=b.lenm;j++){for (int l=1;l<=lenm;l++){res.a[i][j]=(res.a[i][j]+a[i][l]*b.a[l][j]%mod)%mod;}}}return res;}}Matrix operator+(const Matrix &b)const{if (lenn==b.lenn&&lenm==b.lenm){Matrix res;res.lenn=lenn;res.lenm=lenm;for (int i=1;i<=lenn;i++){for (int j=1;j<=lenm;j++){res.a[i][j]=a[i][j]+b.a[i][j];}}return res;}}Matrix operator-(const Matrix &b)const{if (lenn==b.lenn&&lenm==b.lenm){Matrix res;res.lenn=lenn;res.lenm=lenm;for (int i=1;i<=lenn;i++){for (int j=1;j<=lenm;j++){res.a[i][j]=a[i][j]-b.a[i][j];}}return res;}}};
int s[10],n,m,k,d;
int a[25][25];
ll solve(int mask){Matrix e,f,ans;ans.lenn=1;ans.lenm=f.lenn=f.lenm=e.lenn=e.lenm=n;std::vector<int> vis(n+1);for (int i=1;i<=n;i++){for (int j=1;j<=n;j++){e.a[i][j]=a[i][j];}f.a[i][i]=1;ans.a[1][i]=1;}for (int i=1;i<=k;i++){if (mask&(1<<(i-1))){int x=s[i];for (int j=1;j<=n;j++){e.a[x][j]=e.a[j][x]=0;}vis[x]=1;ans.a[1][x]=0;}}int temp=d;while (temp){if (temp&1) f=f*e;e=e*e;temp>>=1;}ans=ans*f;ll sum=0;for (int i=1;i<=n;i++){if (vis[i]) continue;sum=(sum+ans.a[1][i])%mod;}return sum;
}
void yrzr(){std::cin>>n>>m>>k>>d;d--;for (int i=1;i<=k;i++){std::cin>>s[i];}for (int i=1;i<=m;i++){int x,y;std::cin>>x>>y;a[x][y]=a[y][x]=1;}ll ans=0;for (int i=0;i<(1<<k);i++){if (__builtin_popcount(i)&1){ans=(ans-solve(i)+mod)%mod;}else{ans=(ans+solve(i))%mod;}}std::cout<<ans;
}
相关文章:

2023湖南省赛游记/题解
省赛拖了大哥们的后腿,感觉随便补个正常一队水平的人,我们一队肯定能AK。只能说自己真的菜,全程帮不上什么忙,还负贡献,真的想笑 B 暴力sg #include <bits/stdc.h> #define ll long long #define ull unsigned…...

海信电视U8KL使用体验:参数卷,画质技术也独有!
每个家庭成员对电视都有不同需求,如何能做到兼顾?看似需求众口难调,其实一台海信电视就能满足所有啦。 海信电视的参数不仅是最卷的,同时画质技术还是国内独有的,能把这样一台优秀的电视搬回家,无论电影、…...

E. Mishap in Club
题目: 样例1: 输入 --输出 1 样例2: 输入 --- 输出 3 思路: 数学贪心模拟思路,由于不知道在俱乐部的人数和在外面的人数,又要尽可能少的人数,那么定义两个变量,一个是里面的人数 i…...
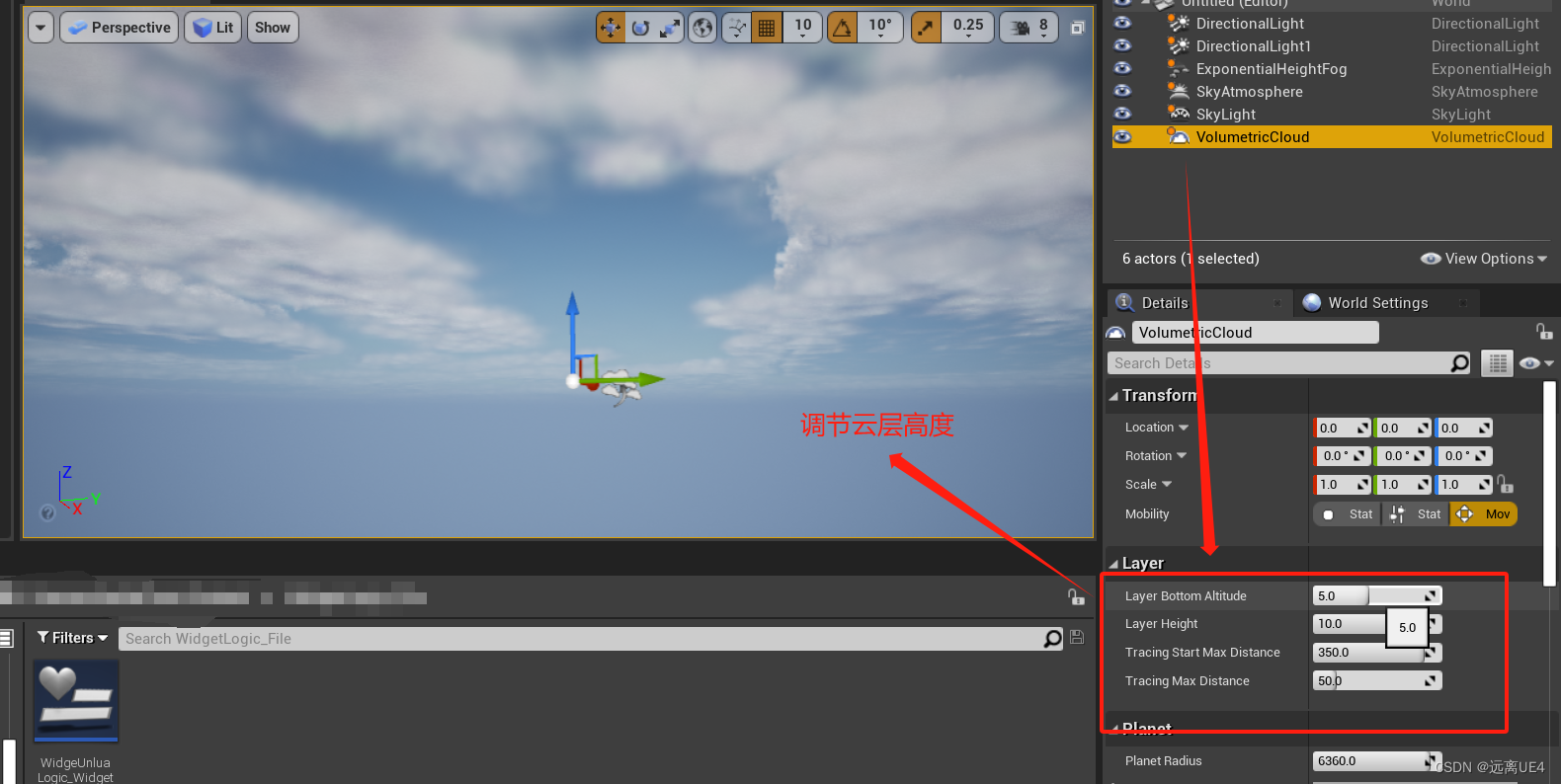
UE4 自带体积云应用
新建空关卡 点击该选项 全部点击一遍 拖进场景...
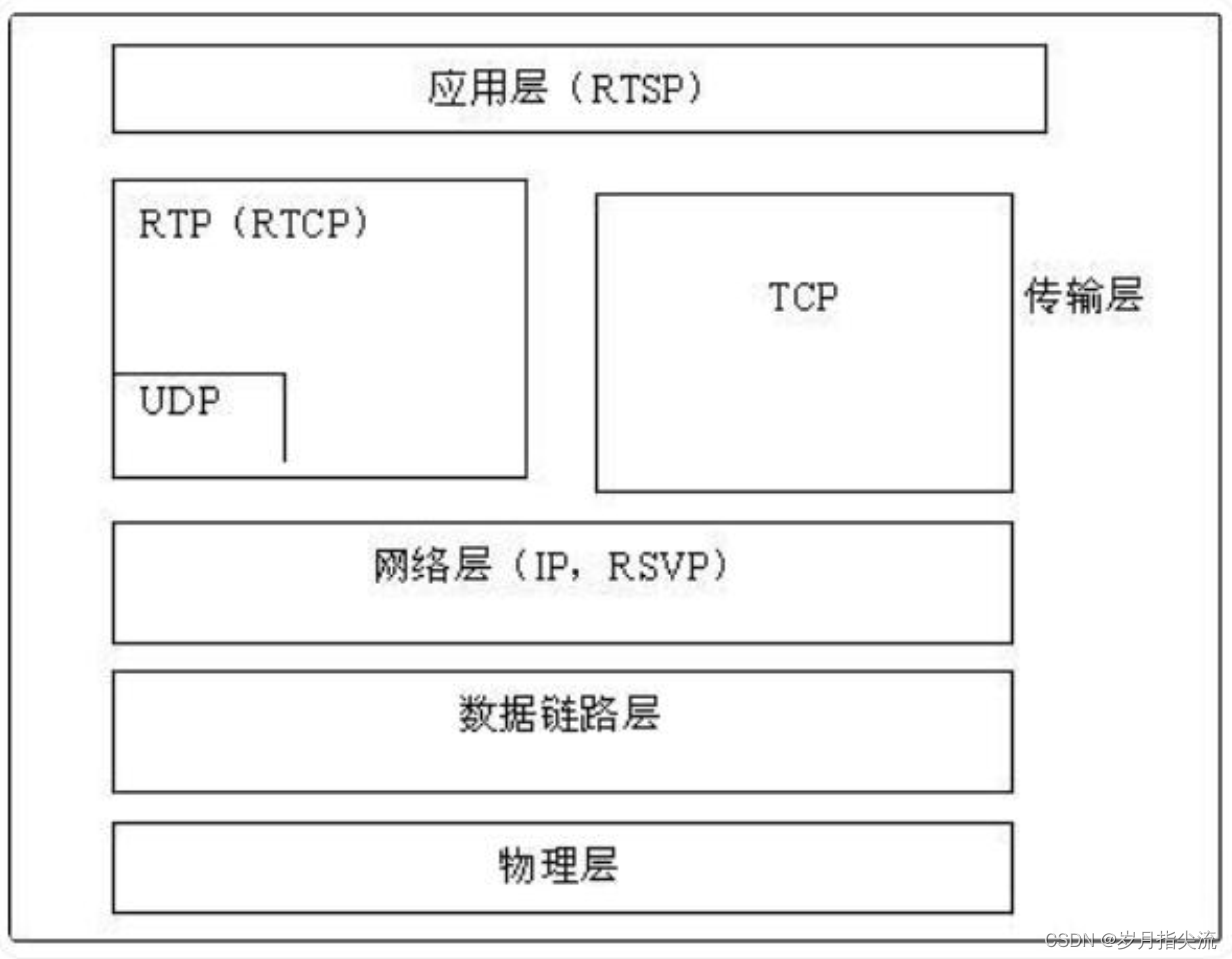
RTP/RTCP 协议讲解
文章目录 前言一、RTP 协议1、RTP 协议概述2、RTP 工作机制3、RTP 协议的报文结构4、wireshark 抓取 RTP 报文 二、RTCP 协议1、RTCP 协议概述2、RTCP 工作机制3、RTCP 数据报4、wireshark 抓取 RTCP 报文 三、RTSP 和 RTP 的关系四、易混淆概念1、RTP over UDP 和 RTP over RT…...

倒计时15天!百度世界2023抢先看
近日消息,在10月17日即将举办的百度世界2023上,百度创始人、董事长兼首席执行官李彦宏将带来主题演讲,“手把手教你做AI原生应用”。 增设社会报名,有机会获得精美伴手礼 目前,百度世界大会已经开放公众参会报名&…...
数据类型和命令(数据类型 二))
Redis 哈希(Hash)数据类型和命令(数据类型 二)
基本概念 Hash是一个键值对的集合,其中每个键都是唯一的。每个键都可以关联多个字段和值,这使得Hash非常适合存储对象或结构化数据。 常用命令 存储、获取、删除:hset、hget、hdel # 添加键为name值为lin hset student name lin # 获取 h…...
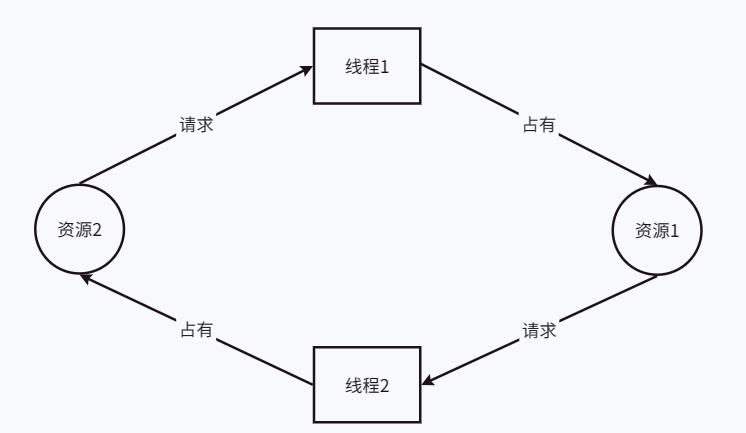
[Linux]线程互斥
[Linux]线程互斥 文章目录 [Linux]线程互斥线程并发访问问题线程互斥控制--加锁pthread_mutex_init函数pthread_mutex_destroy函数pthread_mutex_lock函数pthread_mutex_unlock函数锁相关函数使用示例使用锁的细节加锁解锁的实现原理 线程安全概念常见的线程不安全的情况常见的…...

leetcode-239-滑动窗口最大值
题意描述: 给你一个整数数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。 返回 滑动窗口中的最大值 。 示例: 输入:nums [1,3,-1,…...

基于大语言模型的智能问答系统应该包含哪些环节?
一个完整的基于 LLM 的端到端问答系统,应该包括用户输入检验、问题分流、模型响应、回答质量评估、Prompt 迭代、回归测试,随着规模增大,围绕 Prompt 的版本管理、自动化测试和安全防护也是重要的话题,本篇文章就来探索下这个过程…...

【Cesium创造属于你的地球】相机系统
相机系统里面有setView,flyTo,lookAt,viewBoundingsphere这几种方法,以下是相关的使用方法,学起来!!! setView 该方法可以直接切换相机视口,从而不需要通过一个飞入的效…...

运维困局下确保系统稳定的可行性
业务高速发展背后的困局 随着业务的快速发展,运维体系也逐步的完善起来。业务的稳定性和服务质量也在监控、可用性等体系的相互环抱下健康地成长。所有的问题、故障及影响稳定性的因素都在可控、可收敛的范围内,一切都向着好的方向发展。 这一切的背后…...
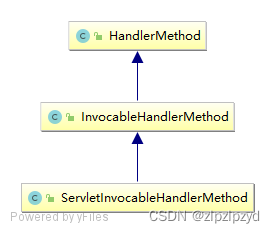
springmvc中DispatcherServlet关键对象
以下代码为 spring boot 2.7.15 中自带的 spring 5.3.29 RequestMappingInfo 请求方法相关信息封装,对应的信息解析在 RequestMappingHandlerMapping 的 createRequestMappingInfo() 中实现。 对于 RequestMapping 赋值的相关信息进行解析 protected RequestMappi…...

某微e-office协同管理系统存在任意文件读取漏洞复现 CNVD-2022-07603
目录 1.漏洞概述 2.影响版本 3.漏洞等级 4.漏洞复现 5.Nuclei自动化扫描POC 某微e-office协同管理系统存在任意文件读取漏洞分析 CNVD-2022-07603https://blog.csdn.net/qq_41490561/article/details/133469649...
消息驱动 —— SpringCloud Stream
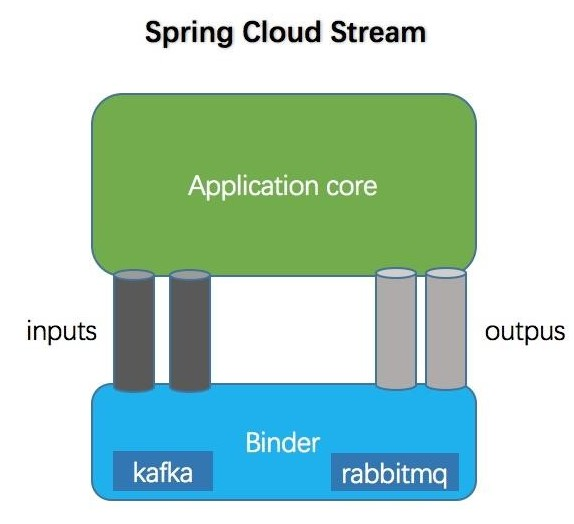
Stream 简介 Spring Cloud Stream 是用于构建消息驱动的微服务应用程序的框架,提供了多种中间件的合理配置 Spring Cloud Stream 包含以下核心概念: Destination Binders:目标绑定器,目标指的是 Kafka 或者 RabbitMQ࿰…...

使用Apache HttpClient爬取网页内容的详细步骤解析与案例示例
Apache HttpClient是一个功能强大的开源HTTP客户端库,本文将详细介绍如何使用Apache HttpClient来爬取网页内容的步骤,并提供三个详细的案例示例,帮助读者更好地理解和应用。 一、导入Apache HttpClient库 在项目的pom.xml文件中添加依赖&a…...
传输层协议—UDP协议
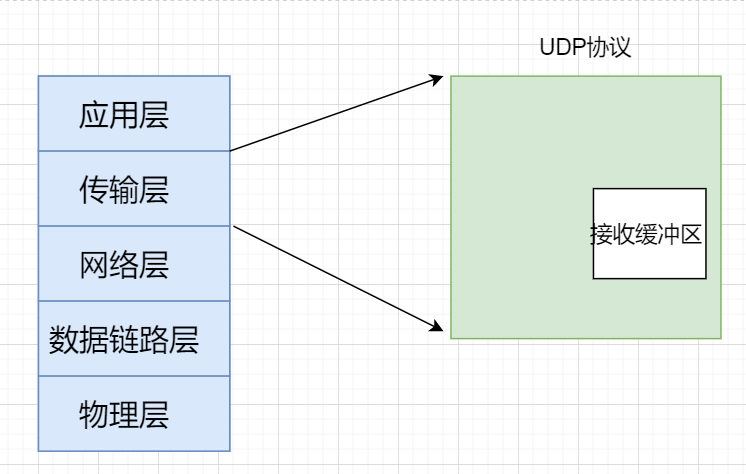
传输层协议—UDP协议 文章目录 传输层协议—UDP协议传输层再谈端口号端口号范围划分pidofnetstat UDP协议端格式UDP报文UDP特点UDP缓冲区基于UDP的应用层协议 传输层 在学习HTTP/HTTPS等应用层协议时,为了方便理解,可以简单认为HTTP将请求和响应直接发送…...

【改造中序遍历】 538. 把二叉搜索树转换为累加树
538. 把二叉搜索树转换为累加树 解题思路 改造中序遍历算法因为中序遍历的结果都是有顺序的 升序排序,那么如果先遍历右子树 在遍历左子树 那么结果就是降序的最后我们设置一个变量 累加所有的中间值 那么得到的结果就是比当前节点大的所有节点的值 /*** Definiti…...

2022年11月工作经历
11月 招聘 最近招聘C程序员和黑盒测试员。由于第一次招聘不知道如何处理,不断和同事沟通,摸索出一套简单的规则。C程序员:力扣随机第二题,如果运气不好可以再随机一两次。黑盒测试员:力扣随机第二题或第三题ÿ…...

使用广播信道的数据链路层
使用广播信道的数据链路层 广播信道可以一对多通信。局域网使用的就是广播信道。局域网最主要的特点就是网络为一个单位所拥有,且地理范围和站点数目有限。局域网可按网络拓扑进行分为星形网、环形网、总线网。传统的以太网就是总线网,后来又演变为星…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...
