【C. Build Permutation】(整数理论、构造、思维)
链接
理论基础
结论:在区间[n,2n]上,至少存在一个完全平方数。结论:在区间[n,2n]上,至少存在一个完全平方数。结论:在区间[n,2n]上,至少存在一个完全平方数。
构造⌈n⌉2构造\lceil \sqrt{n}\rceil^2构造⌈n⌉2
∵n⩽⌈n⌉\because \sqrt n \leqslant \lceil \sqrt{n}\rceil∵n⩽⌈n⌉
∴n⩽⌈n⌉2\therefore n\leqslant \lceil \sqrt{n}\rceil^2∴n⩽⌈n⌉2
⌈n⌉⩽n+1\lceil \sqrt{n}\rceil \leqslant \sqrt{n} + 1⌈n⌉⩽n+1
⌈n⌉2⩽n+2n+1\lceil \sqrt{n}\rceil^2 \leqslant n+2\sqrt n+1⌈n⌉2⩽n+2n+1
何时2n⩾n+2n+1何时2n\geqslant n+2\sqrt n+1何时2n⩾n+2n+1
即n−2n−1⩾0即n-2\sqrt n-1\geqslant0即n−2n−1⩾0
(n−1)2⩾2(\sqrt n-1)^2\geqslant 2(n−1)2⩾2
当n⩾7的时候成立,而且取不到等号当n\geqslant 7的时候成立,而且取不到等号当n⩾7的时候成立,而且取不到等号
然后枚举0到6所有数0123456发现均可以找到不到2n的平方数然后枚举0到6所有数0~1~2~3~4~5~6发现均可以找到不到2n的平方数然后枚举0到6所有数0 1 2 3 4 5 6发现均可以找到不到2n的平方数
分别为−−−−−−0126543分别为------0~1~2~6~5~4~3分别为−−−−−−0 1 2 6 5 4 3
分析
这里从最后的数开始寻找,[n, 2n],必定有一个平方数,与这个数配对的数可以是0~n的所有数,我们从后往前配对,一旦配对成功就倒置使得这些数的和均为平方数即可。面对剩余的序列如法炮制,同样是从最后一个开始找然后配对使得这些数的和均在以最后一个数为n的[n, 2n]区间内的一个数,由于倒置的和均等于头尾的和所有中间这部分倒置的和就是合法的。
实现
#include <bits/stdc++.h>
#define ll long long
#define ls (p << 1)
#define rs (p << 1 | 1)
#define inf 0x3f3f3f3f
#define INF 0x3f3f3f3f3f3f3f3f
using namespace std;
typedef pair<int, int> PII;
const int N = 2e5 + 5;
int vis[N];
bool check(int x) {int sq = sqrt(x);return sq * sq == x;
}
void solve() {int n;cin >> n;for (int i = 0; i < n; i++) vis[i] = 0;map<int, int> mp; for (int i = n - 1; i >= 0; i--) {if (vis[i]) continue;//如果已经配对过的话int p = i;//从这个点开始往前找while (!check(p + i)) p--;//找到第一个恰好是平方的数int sum = p + i;//注意这里是ifor (int j = p; j <= i; j++) {//到i不是到n-1vis[j] = 1;mp[j] = sum - j;}}for (int i = 0; i < n; i++) {cout << mp[i] << " \n"[i == n - 1];}
}
int main(){ios::sync_with_stdio(false);cin.tie(0);int T = 1;cin >> T;while (T--) solve();return 0;
}
相关文章:
)
【C. Build Permutation】(整数理论、构造、思维)
链接 理论基础 结论:在区间[n,2n]上,至少存在一个完全平方数。结论:在区间[n,2n]上,至少存在一个完全平方数。结论:在区间[n,2n]上,至少存在一个完全平方数。 构造⌈n⌉2构造\lceil \sqrt{n}\rceil^2构造⌈…...
)
前端面试题:事件循环(Eventloop)
什么是事件循环?如何理解事件循环?事件循环原理如何描述?事件循环涉及了很多知识点,想要彻底掌握JS事件循环原理必须要掌握以下知识点:同步任务、异步任务、宏任务、微任务、任务队列、执行栈、js运行机制、EventLoop。 1.事件循…...

jmeter接口自动化测试框架
接口测试可以分为两部分: 一是线上接口(生产环境)自动化测试,需要自动定时执行,每5分钟自动执行一次,相当于每5分钟就检查一遍线上的接口是否正常,有异常能够及时发现,不至于影响用…...
树莓派CM4基础设置
安装系统1.1 软件和硬件准备硬件:CM4(4GB DDR32GB EMMC 板载WIFI和蓝牙)CM4-to-Pi4-Adapter软件:Raspberry Pi或者 Win32DiskImagerRaspberry Pi下载链接:点击直接下载Win32DiskImager下载链接:链接&#x…...

JS 合并数组的三大方式
1. 数组的不可变合并 1.1使用扩展运算符进行合并 如果您想知道一种在JavaScript中合并数组的好方法,那么请记住使用扩展操作符进行合并。 在数组字面量中写入两个或更多带有扩展操作符…前缀的数组,JavaScript将创建一个合并所有这些数组的新数组: co…...
30岁测试开发年薪不足50万,被面试官嘲讽混得太差?
近日,有网友发帖称:“30岁去应聘测试开发,拿不到七八十万的年薪确实有点丢人了,还被面试官diss混得太差了”,网友们看完都炸了。 来看看网友们都是怎么说的。 有网友说: 扯淡 有网友气到: 那拿…...

【C语言】多线程
多线程线程线程的优点C语言多线程创建线程终止线程连接和分离线程开启一个线程最基本的多线程实现开启两个线程多线程进行协同运算无参数传递的线程并发编程实例简单参数传递的线程并发编程实例结构体参数传递的线程并发编程实例线程的连接编程实例信号量同步进行写入互斥信号量…...

CDGA|浅谈“以治促用,以用促治”的数据治理战略
数据治理夯实企业数字化转型基础。采取“以治促用,以用促治”的数据治理战略,可以充分释放了企业核心运行要素的活力。 “以治促用”是指通过建立在数据治理链路及用户多维评估系统的基础上,对数据资产重新进行价值识别,推进高价值…...
Apifox-比postman更优秀的接口自动化测试平台
一、Apifox介绍 Apifox 是 API 文档、API 调试、API Mock、API 自动化测试一体化协作平台,定位 Postman Swagger Mock JMeter。通过一套系统、一份数据,解决多个系统之间的数据同步问题。只要定义好 API 文档,API 调试、API 数据 Mock、A…...
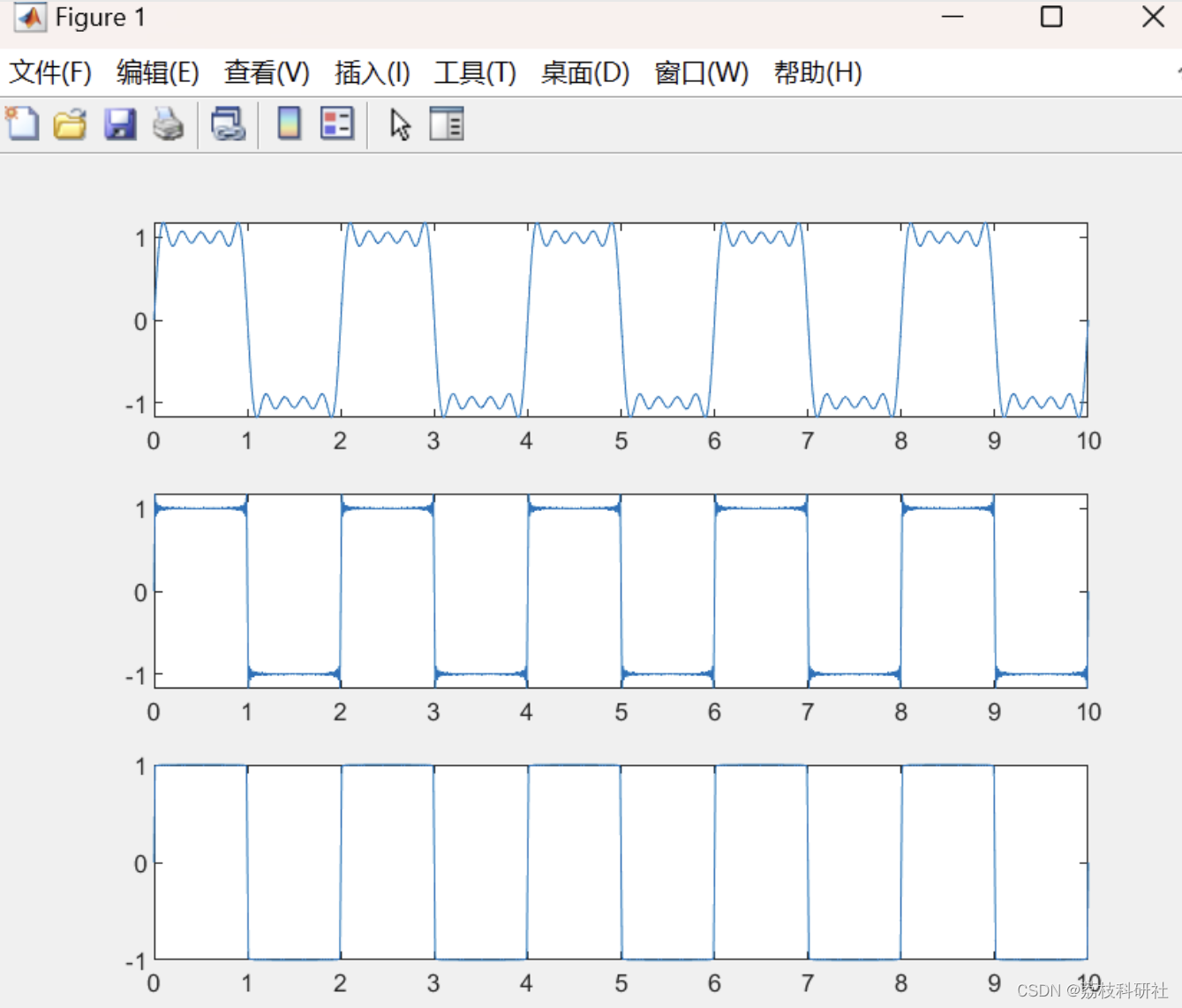
周期矩形波的傅里叶级数展开(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
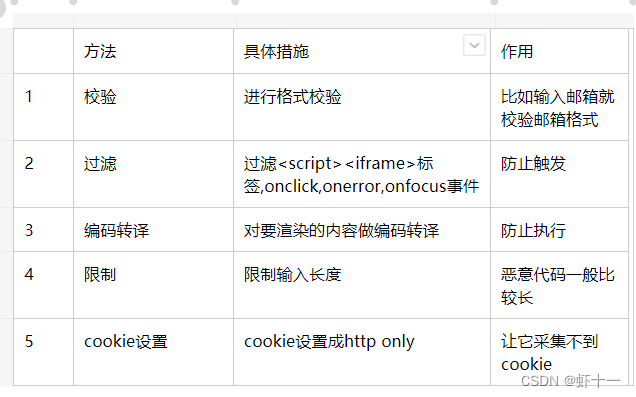
前端预防XSS攻击全攻略
如何防止XSS攻击 一、是撒子 XSS攻击(跨站点脚本攻击),就是黑客恶意篡改你网页的前端代码,在里面注入一些恶意的 htmljavascript的脚本,并在你的浏览器内运行,获取你的信息,或者进行一些恶意操…...
)
JUC(一)
1.AQS原理 1.1.概述 1>.AQS全称是 AbstractQueuedSynchronizer,是阻塞式锁和相关的同步器工具的框架; 2>.特点: ①.用state属性来表示资源的状态(分独占模式和共享模式),子类需要定义如何维护这个状态,控制如何获取锁和释放锁; getState: 获取state状态;setStata: 设置…...

API接口——睡眠带开放能力
本文介绍睡眠带相关接口。 API 列表 请求方法API描述GET/v1.0/devices/{device_id}/sleep/daily-reports获取日睡眠报告。GET/v1.0/devices/{device_id}/sleep/monthly-reports获取月睡眠报告。GET/v1.0/devices/{device_id}/sleep/24h-reports获取 24 小时睡眠报告。GET/v1.…...
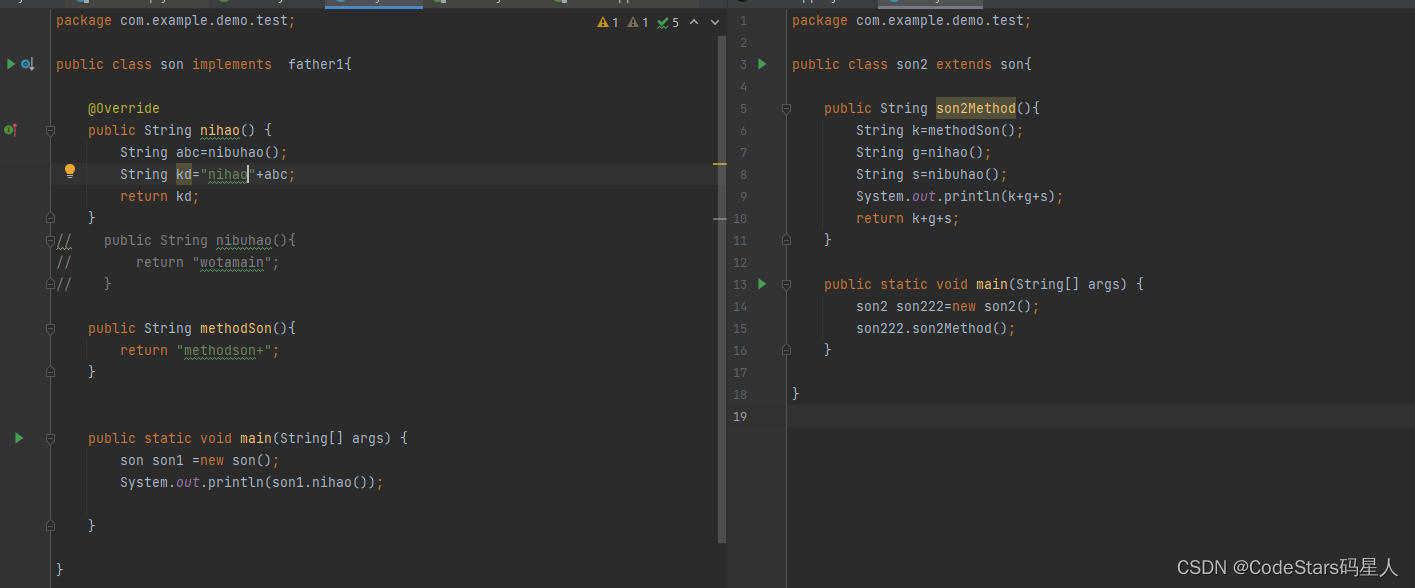
面向对象的一点小想法
接口里的方法可以写也可以不写 如果写的话,那么得是默认方法,需要在前面加个default 对于默认方法,能够重写,或者直接继承(也就是直接用) 比如下面: 就直接调用了接口的默认函数nibuhao&#…...

数据仓库工作问题总结
1. ODS 层采用什么压缩方式和存储格式? 压缩采用 Snappy ,存储采用 orc ,压缩比是 100g 数据压缩完 10g 左右。 2. DWD 层做了哪些事? 1.、数据清洗 空值去除过滤核心字段无意义的数据,比如订单表中订单 id 为 nul…...

Java常用算法
关于时间复杂度: 平方阶 (O(n2)) 排序 各类简单排序:直接插入、直接选择和冒泡排序。线性对数阶 (O(nlog2n)) 排序 快速排序、堆排序和归并排序。O(n1)) 排序, 是介于 0 和 1 之间的常数。希尔排序。线性阶 (O(n)) 排序 基数排序,…...

插画网课平台排名
插画网课平台哪个好,插画网课排名靠前的有哪些,今天给大家梳理了国内5家专业的插画网课平台,各有优势和特色,给学插画的小伙伴提供选择,报插画网课一定要选择靠谱的,否则人钱两空泪两行! 一&am…...

雷达、定位、跟踪等信号处理邻域SCI期刊整理及推荐
雷达邻域SCI期刊整理及推荐:题名、刊物信息、撰写特点、审稿周期及投稿难度总结 定位/跟踪邻域SCI期刊整理及推荐:题名、刊物信息、撰写特点、审稿周期及投稿难度总结 估计/滤波/融合等信号处理邻域SCI期刊整理及推荐:题名、刊物信息、撰写…...

NDK C++ 指针常量 常量指针 常量指针常量
指针常量 常量指针 常量指针常量// 指针常量 常量指针 常量指针常量#include <iostream> #include <string.h> #include <string.h>using namespace std;int main() {// *strcpy (char *__restrict, const char *__restrict);// strcpy()int number 9;int n…...
(一))
常见前端基础面试题(HTML,CSS,JS)(一)
html语义化的理解 代码结构: 使页面在没有css的情况下,也能够呈现出好的内容结构 有利于SEO: 爬虫根据标签来分配关键字的权重,因此可以和搜索引擎建立良好的沟通,帮助爬虫抓取更多的有效信息 方便其他设备解析: 如屏幕阅读器、盲人阅读器、移动设备等,…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...
