数学建模Matlab之评价类方法
大部分方法来自于http://t.csdnimg.cn/P5zOD
层次分析法
层次分析法(Analytic Hierarchy Process, AHP)是一种结构决策的定量方法,主要用于处理复杂问题的决策分析。它将问题分解为目标、准则和方案等不同层次,通过成对比较和计算权重值来实现决策问题的定量分析。
主要步骤
-
建立层次结构模型:
- 首先确定决策问题的目标、准则和方案等不同层次,并构建层次结构模型。这个在代码中是没有的,需要提前进行。
-
成对比较构建判断矩阵:
- 通过成对比较各准则和方案的相对重要性,构建判断矩阵。
- 在层次分析法代码示例中,判断矩阵
A由用户输入。
-
计算权重值:
- 使用特征值方法计算判断矩阵的权重值。
- 示例代码中,通过求
A的最大特征值B和对应的特征向量C来计算权重值Q。
-
一致性检验:
- 进行一致性检验来确保判断矩阵的合理性。
- 代码中,使用一致性指标
CI和CR进行检验,如果CR<0.10,判断矩阵通过一致性检验。
-
结果输出:
- 输出各向量的权重向量
Q,表示每个准则或方案的相对重要性。 - 如果判断矩阵未通过一致性检验,需要对判断矩阵重新构造。
- 输出各向量的权重向量
代码示例
clc;
clear;
% 判断矩阵A,必须保证判断矩阵是互反的。每个元素 A(i, j) 表示第 i 个指标相对于第 j 个指标的重要性。
A= [1 3 5 51/3 1 3 51/5 1/3 1 31/5 1/5 1/3 1];
[m,n]=size(A); %获取指标个数%RI 是一个随机一致性指数,它是用来进行一致性检验的。每个值 RI(n) 对应于一个n阶判断矩阵的一致性检验的标准值。
% RI 数组中只包含了11个值,这是因为通常情况下,判断矩阵的阶数不会超过11。如果有更多的指标,您可能需要查找或计算相应阶数的 RI 值。
RI=[0 0 0.58 0.90 1.12 1.24 1.32 1.41 1.45 1.49 1.51];
R=rank(A); %求判断矩阵的秩
[V,D]=eig(A); %求判断矩阵的特征值和特征向量,V特征值,D特征向量;
tz=max(D);
B=max(tz); %最大特征值
[row, col]=find(D==B); %最大特征值所在位置
C=V(:,col); %对应特征向量
CI=(B-n)/(n-1); %计算一致性检验指标CI
CR=CI/RI(1,n);
%代码进行一致性检验来确保判断矩阵的合理性。
%如果一致性检验通过(即 CR < 0.10),则继续计算权重;否则,需要重新构造判断矩阵。
if CR<0.10disp('CI=');disp(CI);disp('CR=');disp(CR);disp('对比矩阵A通过一致性检验,各向量权重向量Q为:');Q=zeros(n,1);for i=1:nQ(i,1)=C(i,1)/sum(C(:,1)); %特征向量标准化endQ' %输出权重向量
elsedisp('对比矩阵A未通过一致性检验,需对对比矩阵A重新构造');
end
sc = Q';
其中,有以下注意事项:
1.判断矩阵A,必须保证判断矩阵是互反的。
2.RI 是一个随机一致性指数,它是用来进行一致性检验的。RI 数组中只包含了11个值,这是因为通常情况下,判断矩阵的阶数不会超过11。如果有更多的指标,可能需要查找或计算相应阶数的 RI 值。
3.数模论文中只要使用到了层次分析法,就必须画层次结构图,无论文章是否需要压缩篇幅,这和层次分析法的使用绑在一起。
熵权法
熵权法同样是一种决策分析的方法,用于确定各个决策指标的权重。该方法主要依赖于信息熵的概念。在决策分析中,信息熵用来度量某个决策指标的离散程度。如果一个指标的变化越大(即更离散),那么它应该被赋予更大的权重。熵权法通过计算每个指标的信息熵来确定各个指标的权重。
主要步骤
-
非负数化和归一化处理:
- 代码中,首先进行了对原始数据的非负数化和归一化处理(
x(:,i)=(x(:,i)-min(x(:,i)))/(max(x(:,i))-min(x(:,i)))+1),使得所有数据值介于1和2之间。
- 代码中,首先进行了对原始数据的非负数化和归一化处理(
-
计算概率值:
- 然后,计算每个数据点在其所在列的比例(
p(i,j)=x(i,j)/sum(x(:,j))),这可以被看作是数据点的概率值。
- 然后,计算每个数据点在其所在列的比例(
-
计算信息熵:
- 接下来,使用计算得到的概率值来计算每列(即每个决策指标)的信息熵(
E(j)=-k*sum(e(:,j)))。信息熵被用来度量一个随机变量的不确定性,即决策指标的离散程度。
- 接下来,使用计算得到的概率值来计算每列(即每个决策指标)的信息熵(
-
计算差异系数:
- 之后,计算每个指标的差异系数(
d=1-E)。差异系数用来度量一个指标与其他指标的差异程度。
- 之后,计算每个指标的差异系数(
-
计算权重:
- 最后,计算每个决策指标的权重(
w(j)=d(j)/sum(d)),这个权重代表了该指标在决策分析中的重要性。
- 最后,计算每个决策指标的权重(
-
计算综合分数:
- 使用计算得到的权重来计算每个数据点的综合分数(
score(i,1)=sum(x(i,:).*w))
- 使用计算得到的权重来计算每个数据点的综合分数(
对于计算综合分数,可能说的比较模糊,作者举个例子,假设我们有以下简化的数据和权重:
x = [
1 2
3 4
] %数据w = [0.3, 0.7] % 权重
则第一个数据点(也就是行向量[1,2],在现实生活中可能代表某一个样本,分量值相当于熵权法的指标值,我们就是在求得各指标的权重后通过权重+样本的指标值求得样本的综合分数的)的综合分数计算如下:
score(1)=(1×0.3)+(2×0.7)=1.7score(1)=(1×0.3)+(2×0.7)=1.7
第二个数据点的综合分数计算如下:
score(2)=(3×0.3)+(4×0.7)=3.7score(2)=(3×0.3)+(4×0.7)=3.7
从而得到综合分数数组 score = [1.7, 3.7]。
通过这种方法,可以利用计算出的权重对每个数据点进行评分,从而进行进一步的分析和决策。
代码示例
x = [
2.41 52.59 0 9.78 1.17
1.42 53.21 0 6.31 1.63
4.71 35.16 1 9.17 3.02
14.69 15.16 2.13 10.35 7.97
0.94 72.99 0 7.39 0.61
1.43 72.62 0 8.16 0.51
2.21 67.5 0 9.84 0.85
3.79 51.21 0 12.95 1.43
1.23 85.09 3.97 4.08 0.13
1.71 82.07 2.88 4.97 0.33
3.63 66.9 3.18 8.57 0.71
5.72 49.77 3.44 10.52 1.83
1.49 79.51 6.53 2.58 0.27
1.66 81.44 5.18 2.74 0.36
2.41 76.32 5.88 4.13 0.54
4.42 59.65 7.64 8.38 1.02
3.27 88.42 3.36 2.85 0.14
11.27 70.05 5.77 6.07 0.19
13.18 62.45 5.66 7.85 0.74
15.83 56.28 2.92 9.97 1.14
11.59 80.23 1.04 3.64 0.2
26.67 55.7 2.02 8.13 0.38
28.51 51.07 2.12 9.66 1.46
3.69 87.26 0 3.12 0.18
3.27 84.43 0 5.43 0.31
3.98 79.99 0 6.62 0.57
1.59 86.5 0 6.14 0.14
4.31 82.26 0 4.71 0.2
4.6 72.79 0 8.27 0.52
4.99 81.93 0 7.52 0.16
4.66 75.09 0 10.24 0.33
5.08 61.02 1.57 15.7 0.53
12.49 83.06 0 1.2 1.06
4.67 92.77 0 0.33 0.58
5.8 90.32 0 0.91 0.8
97.76 0 0 0 2.14
94.75 0 0 1.42 2.83
93.76 0 0 1.18 3.24
3.48 81.43 7.45 1.33 0.14
4.2 80 5.3 2.21 0.18
8.83 71.28 5.34 2.9 0.43
5.39 79.6 6.87 2.64 0.31
7.67 74.74 5.91 3.4 0.66
19.65 55.4 4.87 6.14 1.2
2.63 90.74 3.18 1.42 0.14
2.8 89.7 2.85 1.96 0.14
4.07 85.12 3.43 3.52 0.25
5.7 83.4 0 4.48 0.1
4.03 81.35 0 6.18 0.19
4.11 73.45 0 9.71 0.45
2.78 89.53 0 4.23 0.2
3.92 83.2 0 7.59 0.32
5.21 71.37 3.09 10.29 0.72
18.98 76.81 0 1.05 0.31
19.79 73.56 0 0.88 0.42
19.86 70.07 0 1.72 0.74
16.61 67.57 3.77 3.15 1.16
6.91 82.18 4.19 0 0.1
2.93 83.06 1.93 5.14 0.32
8.47 78.11 4.04 4.02 0.31
12.29 70.48 3.89 4.32 0.69
3.98 84.81 4.76 1.97 0.18
7.67 78.13 4.22 4.57 0.35
14.04 66.89 4.41 6.27 0.47
14.62 59.29 5.28 8.35 0.77
1.97 85.16 4.87 3.27 0.23
2.16 86.83 3.82 2.25 0.15
4.81 74.9 5.05 5.97 0.5
7.44 57.98 6.75 10.73 1.04
2.04 86.01 4.79 2.95 0.13
3.49 79.79 5.67 4.28 0.15
6.47 68.02 6.71 5.74 0.2
7.94 59.12 7.14 5.93 1.42
];[m,n]=size(x);
lamda=ones(1,n); % 人为修权,1代表不修改计算后的指标权重
for i=1:nx(:,i)=(x(:,i)-min(x(:,i)))/(max(x(:,i))-min(x(:,i)))+1; % 对原始数据进行非负数化、归一化处理,值介于1-2之间
end
for i=1:mfor j=1:np(i,j)=x(i,j)/sum(x(:,j));end
end
k=1/log(m);
for i=1:mfor j=1:nif p(i,j)~=0e(i,j)=p(i,j)*log(p(i,j));elsee(i,j)=0;endend
end
for j=1:nE(j)=-k*sum(e(:,j));
end
d=1-E;
for j=1:nw(j)=d(j)/sum(d);% 指标权重计算
end
for j=1:nw(j)=w(j)*lamda(j)/sum(w.*lamda);% 修改指标权重
end
for i=1:mscore(i,1)=sum(x(i,:).*w);% 计算综合分数% 一个数据点对应矩阵每一行数据,根据大量的数据点,确定其权重,然后计算每一个数据点的综合得分(数据点本例中对应四个指标值,分别利用权重求得综合得分
end
disp('各指标权重为:')
disp(w) %权重越大,该指标在决策分析中的重要性越高。
disp('各项综合分数为:')
disp(score) %每个数据点的综合分数。综合分数可以被用来进行进一步的分析或决策。
Out = mean (score,1)相关文章:

数学建模Matlab之评价类方法
大部分方法来自于http://t.csdnimg.cn/P5zOD 层次分析法 层次分析法(Analytic Hierarchy Process, AHP)是一种结构决策的定量方法,主要用于处理复杂问题的决策分析。它将问题分解为目标、准则和方案等不同层次,通过成对比较和计算…...
json能够存储图片吗?
JSON 本身并不适合存储图片,因为它是一种轻量级的数据交换格式,易于阅读和编写,同时也易于机器解析和生成。JSON 数据格式简单,只包含键值对,因此它主要用于存储和传输文本数据。 然而,你可以将图片转换为 …...
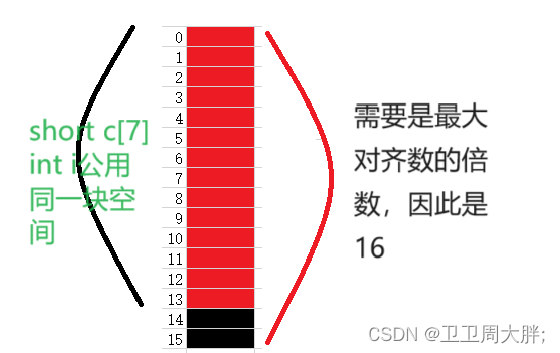
C语言中自定义类型讲解
前言:C语言中拥有三种自定义类型,这三种自定义类型是怎么运用呢?在内存中又是怎么存储的呢?通过这篇文章我们来逐个讲解讲解。 三种类型分别是: 1.结构体 – 通俗的来讲就是可以把不同类型的变量放在一个集合中 2.枚举…...
Win10系统中GPU深度学习环境配置记录
运行环境 系统:Win10 处理器 Intel(R) Core(TM) i7-9700K CPU 3.60GHz 3.60 GHz 机带 RAM 16.0 GB 设备 ID A18D4ED3-8CA1-4DC6-A6EF-04A33043A5EF 产品 ID 00342-35285-64508-AAOEM 系统类型 64 位操作系统, 基于 x64 的处理器 显卡:NVIDIA GeF…...
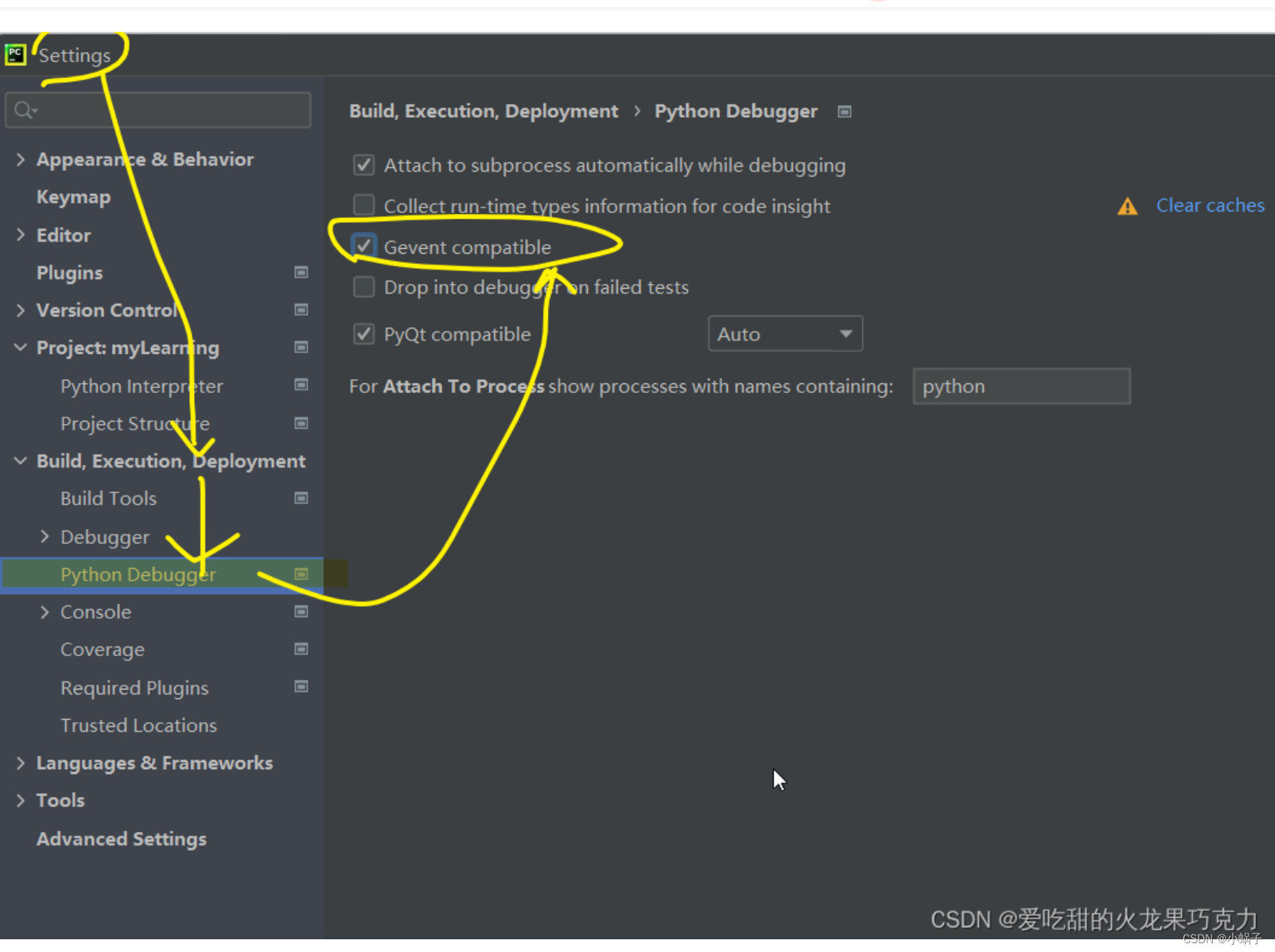
pycharm一直没显示运行步骤,只是出现waiting for process detach
pycharm一直没显示运行步骤,只是出现waiting for process detach;各类音乐免费软件;最棒的下载torch-geometric-CSDN博客(不太推荐)我强烈推荐这个:_waiting for process detachhttps://blog.csdn.net/weix…...

管道读写特点以及设置成非阻塞
管道的读写特点: 使用管道时,需要注意以下几种特殊的情况(假设都是阻塞I/O操作) 1.所有的指向管道写端的文件描述符都关闭了(管道写端引用计数为0),有进程从管道的读端 读数据,那么管…...
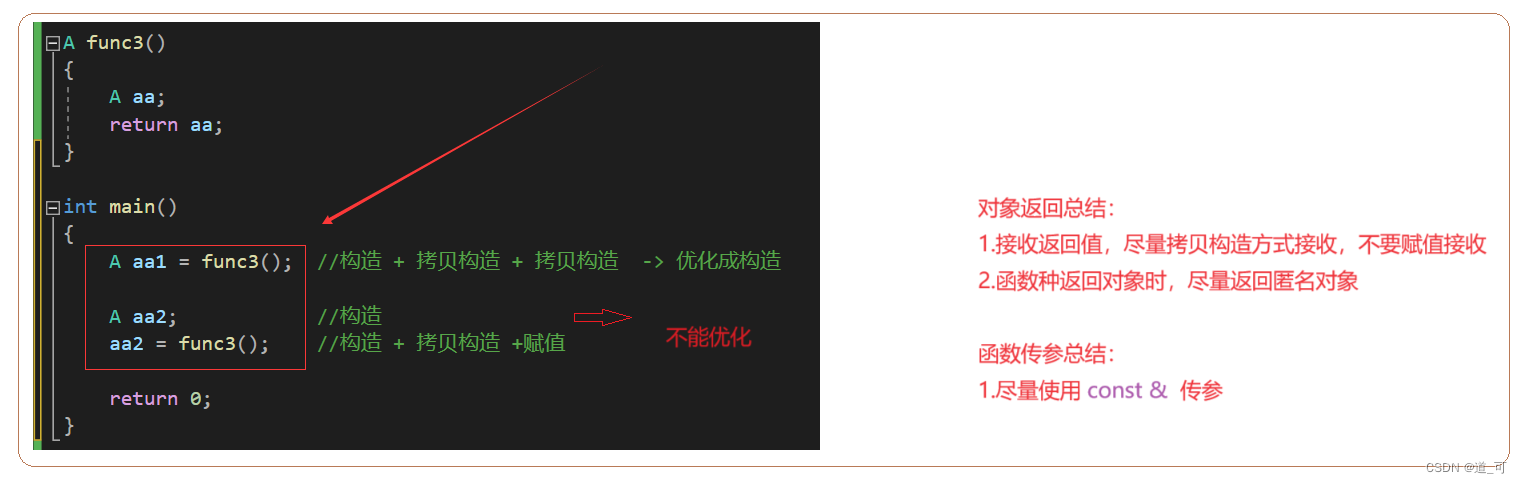
(c++)类和对象 下篇
目录 1.再次了解构造函数 2. Static成员 3. 友元 4. 内部类 5.匿名对象 6.拷贝对象时的一些编译器优化 1.再次了解构造函数 1.1 构造函数体赋值 在创建对象时,编译器通过调用构造函数,给对象中各个成员变量一个合适的初始值。 class Date { pub…...
Tomcat报404问题的原因分析
1.未配置环境变量 按照需求重新配置即可。 2.IIs访问权限问题 注意:这个问题有的博主也写了,但是这个问题可有可无,意思是正常情况下,有没有都是可以访问滴放心 3.端口占用问题 端口占用可能会出现这个问题,因为tomcat的默认端口号是8080,如果在是运行tomcat时计算机的…...

《发现的乐趣》作者费曼(读书笔记)
目录 一、书简介 二、作者理查德•费曼 费曼式思维 教育与传承 三、个人思考 四、笔记 科学家眼中的花之美 关于偏科 父亲教育我的方式 知道一个概念和真正懂得这个概念有很大区别 我没有义务去成全别人对我的期望 诺贝尔奖——够格吗? 探究世界的游戏规…...

第5章-宏观业务分析方法-5.3-主成分分析法
目录 5.3.1 主成分分析简介 协方差矩阵 方差 协方差 协方差矩阵...
IDEA 使用
目录 Git.gitignore 不上传取消idea自动 add file to git撤销commit的内容本地已经有一个开发完成的项目,这个时候想要上传到仓库中 Git .gitignore 不上传 在项目根目录下创建 .gitignore 文件夹,并添加内容: .gitignore取消idea自动 add…...

如何使用 ChatGPT 创建强大的讲故事广告
shadow: 使用AI技术来辅助创作故事越来越流行,从事营销相关工作的人员需要不断适应和学习新的技术和工具,以应对行业的变化和挑战。 如何使用ChatGPT创建讲故事的广告: A. 确定品牌故事和信息传递B. 确定目标受众C. 开发概念D. 使…...
】)
【C语言深入理解指针(4)】
1.回调函数是什么? 回调函数就是一个通过函数指针调用的函数。 如果你把函数的指针(地址)作为参数传递给另⼀个函数,当这个指针被⽤来调⽤其所指向的函数时,被调⽤的函数就是回调函数。回调函数不是由该函数的实现⽅…...

qt中弱属性机制
目录 简介: 详解: 实例: 易错地方: 简介: 使用弱属性机制,可以存储临时的值用于传递判断。可以通过widget->dynamicPropertyNames()列出所有弱属性名称,然后通过widget->proper…...
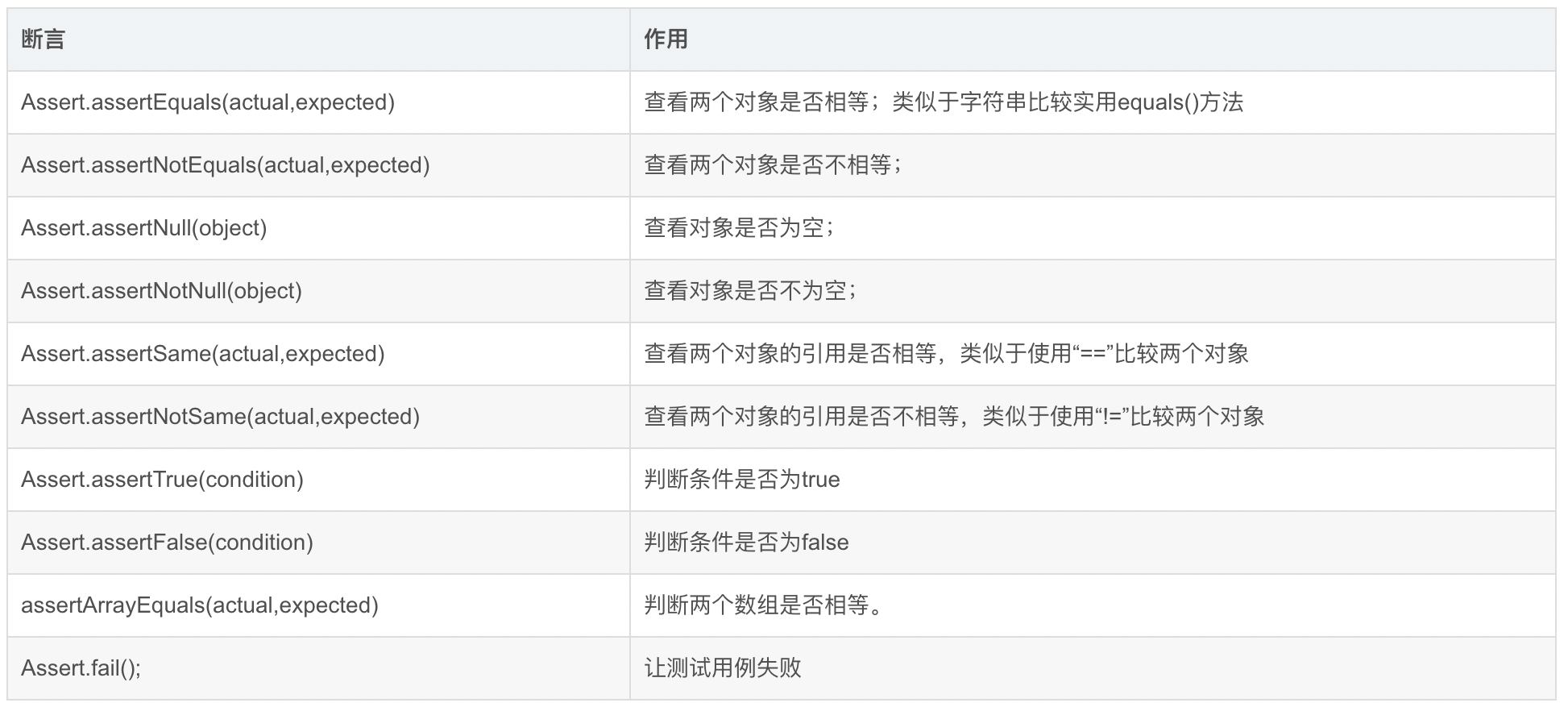
软断言你也学不会
断言是测试用例的一部分,也是测试工程师开发测试用例的核心。断言通常集成在单元测试和集成测试中,断言分为硬断言和软断言。 硬断言是我们狭义上听到的普通断言:当用例运行后得到的[实际]结果与预期结果不匹配时,测试框架将停止测试执行并抛…...
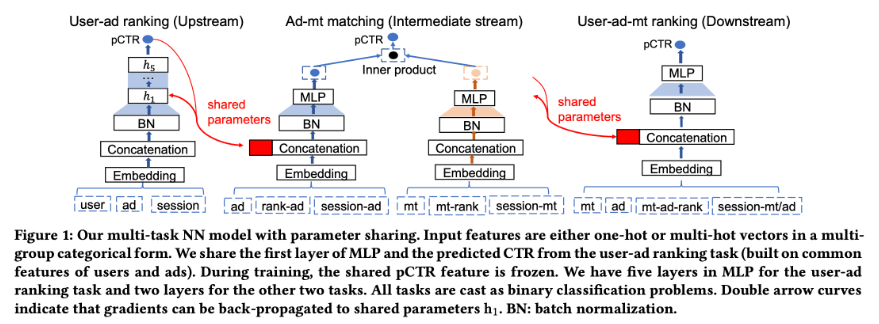
【推荐系统】多任务学习模型
介绍一些多任务学习模型了解是如何处理多任务分支的。 ESSM, Entire Space Multi-Task Model 阿里提出的ESSM全称Entire Space Multi-Task Model,全样本空间的多任务模型,有效地解决了CVR建模(转化率预估)中存在的两个非常重要…...

基于SpringBoot的商品物品产品众筹平台设计与实现(源码+lw+部署文档+讲解等)
文章目录 前言具体实现截图论文参考详细视频演示为什么选择我自己的网站自己的小程序(小蔡coding)有保障的售后福利 代码参考源码获取 前言 💗博主介绍:✌全网粉丝10W,CSDN特邀作者、博客专家、CSDN新星计划导师、全栈领域优质创作…...
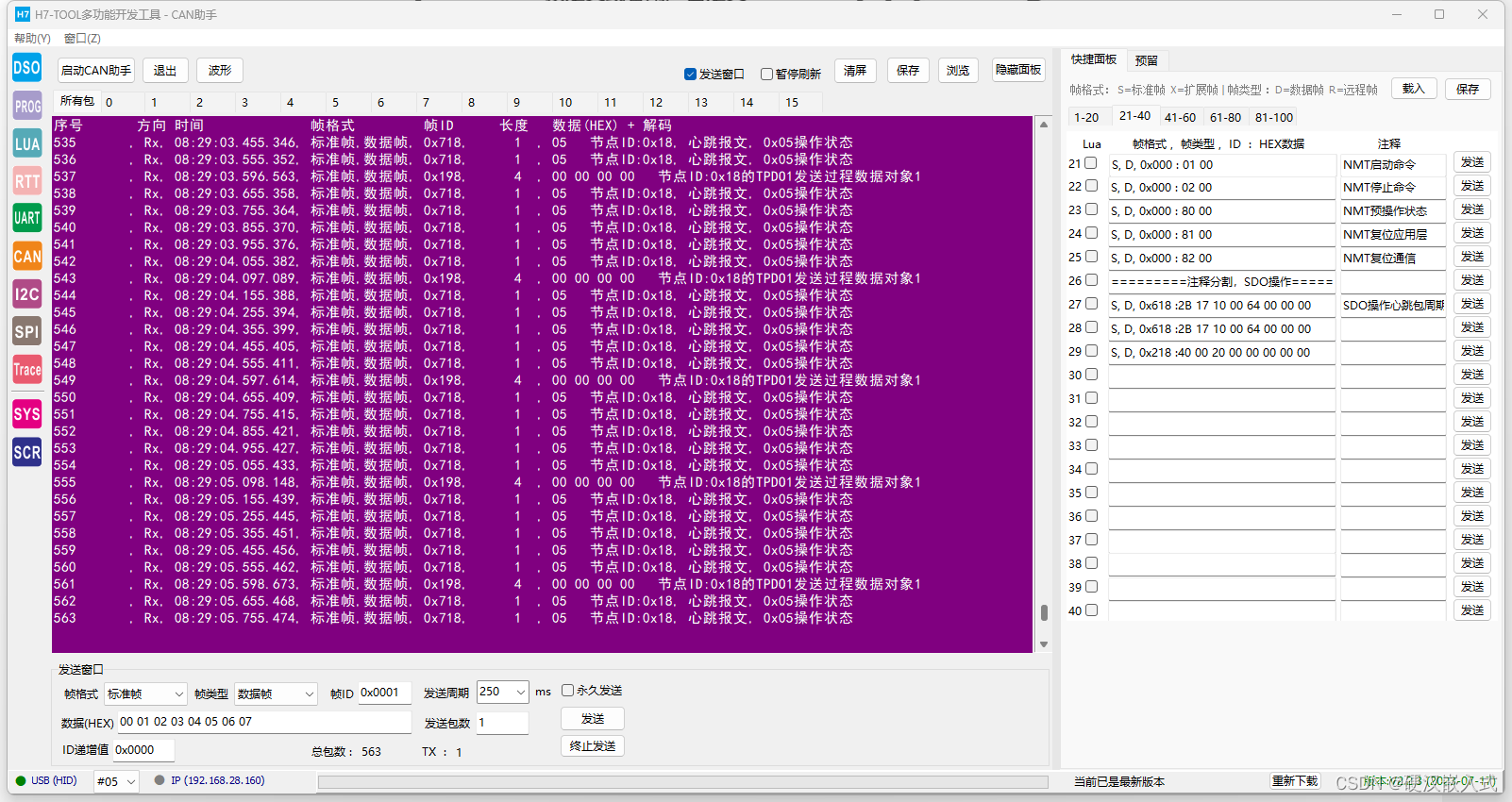
《安富莱嵌入式周报》第323期:NASA开源二代星球探索小车, Matlab2023b,蓝牙照明标准NLC, Xilinx发布电机套件,Clang V17发布
周报汇总地址:嵌入式周报 - uCOS & uCGUI & emWin & embOS & TouchGFX & ThreadX - 硬汉嵌入式论坛 - Powered by Discuz! 视频版: https://www.bilibili.com/video/BV1vp4y1F7qD 《安富莱嵌入式周报》第323期:NASA开源…...

Redis的事务管理
redis也支持事务,但与MySQL等关系型数据库相比,redis的事务比较简单。 一、redis事务的特点 1、redis的事务是一组命令集合 可以把redis的事务看成一个命令的缓存,把一组要执行的命令添加到集合中,然后按顺序一起执行。 2、redi…...
:特殊的WiFi驱动移植方法)
openwrt (一):特殊的WiFi驱动移植方法
openwrt的去驱动移植灵活多样,总体来说只要掌握了官方提供的操作方法即可可简单上手,但是也有一些稍微比较特殊的操作。比如说backport模块。 由于需要兼容很多不同版本的Linux驱动,很多时候需要用到backport。因此,如果已有的项目…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...

Linux 内存管理实战精讲:核心原理与面试常考点全解析
Linux 内存管理实战精讲:核心原理与面试常考点全解析 Linux 内核内存管理是系统设计中最复杂但也最核心的模块之一。它不仅支撑着虚拟内存机制、物理内存分配、进程隔离与资源复用,还直接决定系统运行的性能与稳定性。无论你是嵌入式开发者、内核调试工…...
