基于Matlab实现logistic方法(源码+数据)
Logistic回归是一种常用的分类算法,适用于二分类问题。本文将介绍如何使用Matlab实现Logistic回归方法,并通过一个示例演示其应用。
文章目录
- 引言
- 实现步骤
- 1. 数据准备
- 2. 特征缩放
- 3. 模型训练
- 4. 模型评估
- 源码+数据下载
引言
Logistic回归是一种广泛应用于机器学习和统计学的分类算法。它通过将线性回归的输出通过一个逻辑函数(也称为sigmoid函数)进行映射,将连续的输出转换为概率值,从而进行分类。在本文中,我们将使用Matlab实现Logistic回归方法,并通过一个具体的示例来演示其应用。
实现步骤
1. 数据准备
首先,我们需要准备用于训练和测试的数据集。这个数据集应该包含特征(自变量)和目标变量(因变量)。在本示例中,我们将使用一个包含两个特征和二分类目标变量的数据集。
2. 特征缩放
为了提高算法的性能,我们通常需要对特征进行缩放。这可以通过将每个特征的值除以其标准差来实现。Matlab提供了zscore函数来实现特征缩放。
3. 模型训练
在Logistic回归中,我们需要找到一组最佳的权重参数,使得模型能够最好地拟合训练数据。这可以通过最小化成本函数来实现,其中成本函数通常使用交叉熵损失函数。
在Matlab中,我们可以使用fitglm函数来训练Logistic回归模型。该函数基于最大似然估计方法,使用迭代的方式来找到最佳的权重参数。
4. 模型评估
在模型训练完成后,我们需要评估模型的性能。常用的评估指标包括准确率、精确率、召回率和F1分数等。Matlab提供了一系列函数来计算这些指标,如confusionmat、accuracy、precision、recall和f1score等。
源码+数据下载
基于Matlab实现logistic方法(源码+数据):https://download.csdn.net/download/m0_62143653/88366382
相关文章:
)
基于Matlab实现logistic方法(源码+数据)
Logistic回归是一种常用的分类算法,适用于二分类问题。本文将介绍如何使用Matlab实现Logistic回归方法,并通过一个示例演示其应用。 文章目录 引言实现步骤1. 数据准备2. 特征缩放3. 模型训练4. 模型评估 源码数据下载 引言 Logistic回归是一种广泛应用…...
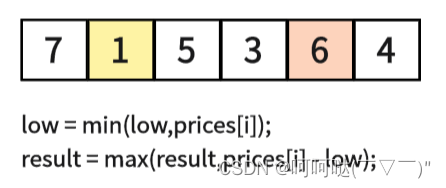
leetCode 121. 买卖股票的最佳时机 贪心算法
给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。 你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。 返回你可以从这笔交易中获取的最大利润。…...

《Oracle系列》Oracle 索引使用情况查看
查询用户的索引 select index_name,table_name,tablespace_name,index_type,uniqueness,statusfrom dba_indexeswhere owner <用户名>;查询用户的索引列 select index_name,table_name,column_name,index_owner,table_ownerfrom dba_ind_columnswhere table_owner &l…...
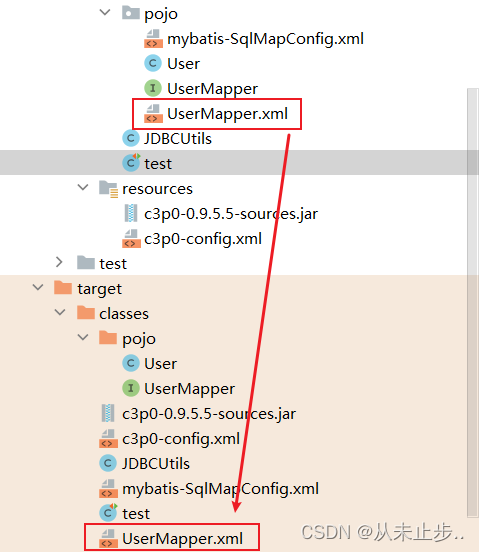
解决Invalid bound statement (not found)错误~
报错如下所示: 找了好久,刚开始以为是名称哪里写的有问题,但仔细检查了好多遍都不是 最后发现了问题如下所示: UserMapper里面的内容被我修改了,但classes中的内容还是原来的内容,所以才导致了编译器报错n…...

基于SpringBoot的反诈宣传平台设计与实现(源码+lw+部署文档+讲解等)
文章目录 前言具体实现截图论文参考详细视频演示为什么选择我自己的网站自己的小程序(小蔡coding)有保障的售后福利 代码参考源码获取 前言 💗博主介绍:✌全网粉丝10W,CSDN特邀作者、博客专家、CSDN新星计划导师、全栈领域优质创作…...

【改进哈里鹰算法(NCHHO)】使用混沌和非线性控制参数来提高哈里鹰算法的优化性能,解决车联网相关的路由问题(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

【C语言】宏定义
🚩 WRITE IN FRONT🚩 🔎 介绍:"謓泽"正在路上朝着"攻城狮"方向"前进四"🔎🏅 荣誉:2021|2022年度博客之星物联网与嵌入式开发TOP5|TOP4、2021|2222年获评百大博…...
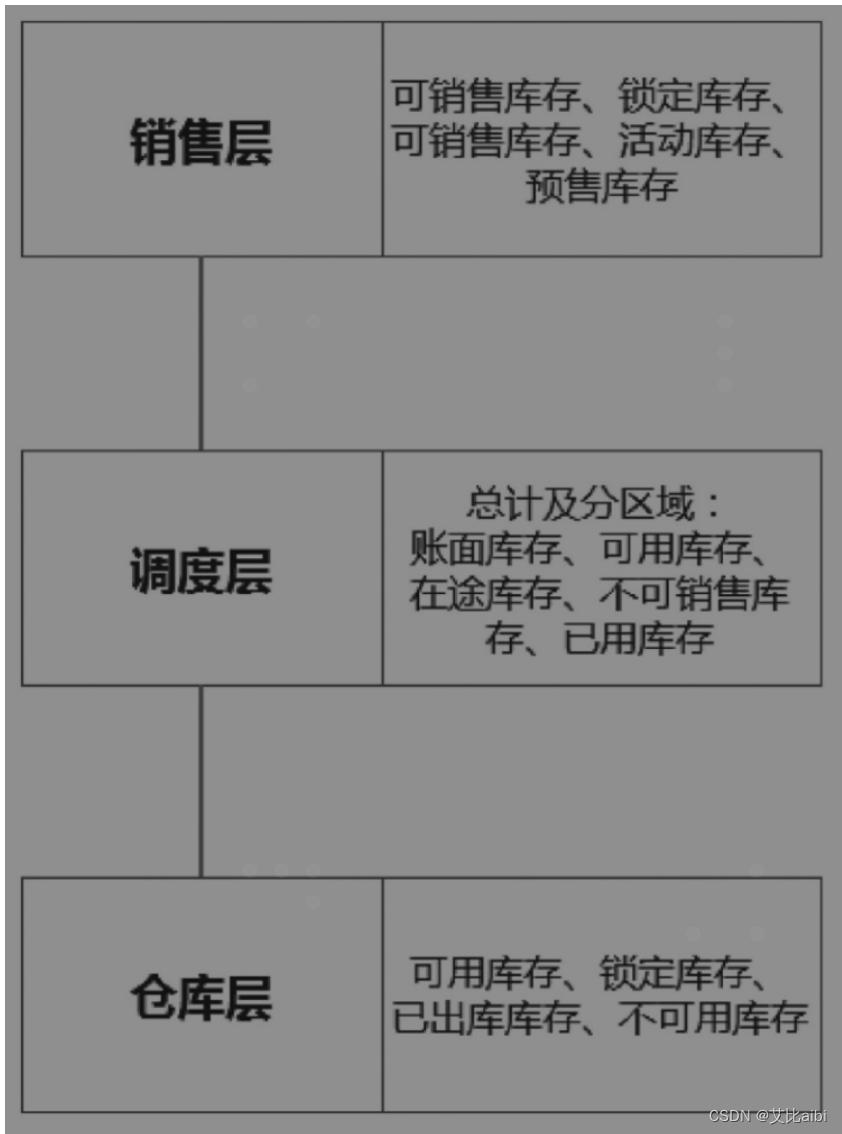
库存三层模型概述
库存分层 (1)电商库存体系分为三层:销售层、调度层、仓库层。 库存三层模型:销售库存,调度层属于订单领域-履约。实物库存属于库存领域 WMS的库存跟调度层是一致的。 但是销售库存跟调度层可能不一致,因为…...

SNERT预备队招新CTF体验赛-Web(SWCTF)
目录 1、F12 2、robots 3、game1-喂青蛙 4、game 2 - flap bird 5、game 3 - Clash 6、Get&Post 7、sql (1)手工注入 (2)工具注入 8、命令执行漏洞 9、文件上传漏洞 10、文件泄露 11、php反序列化漏洞 12、PHP绕…...
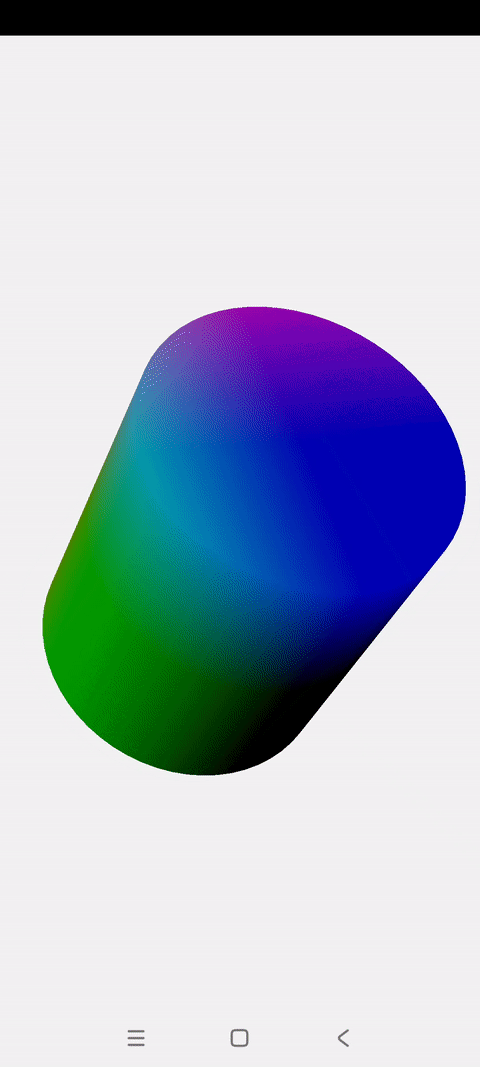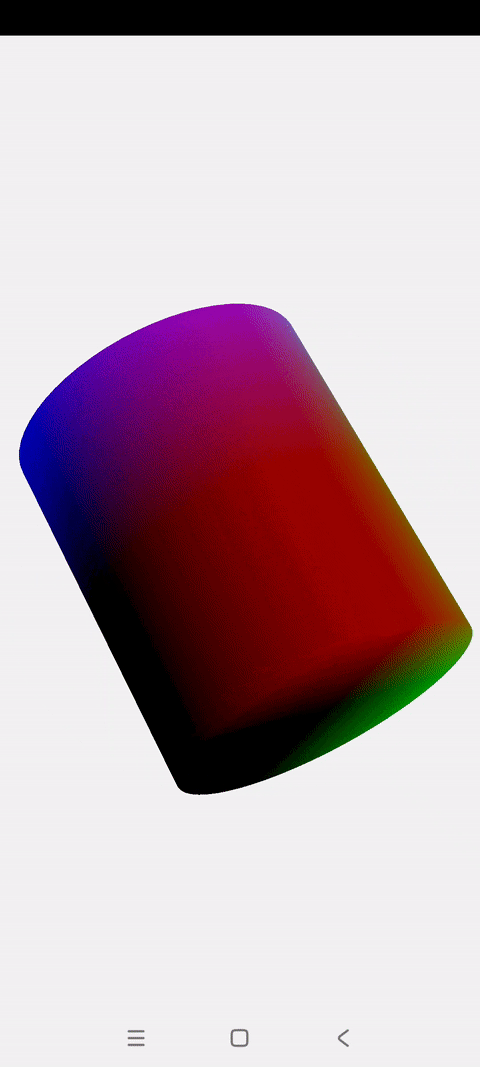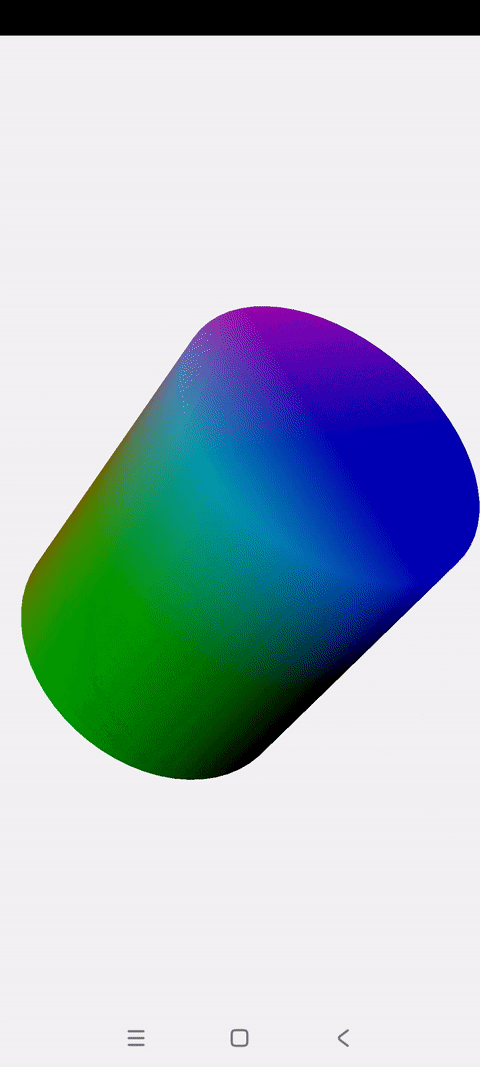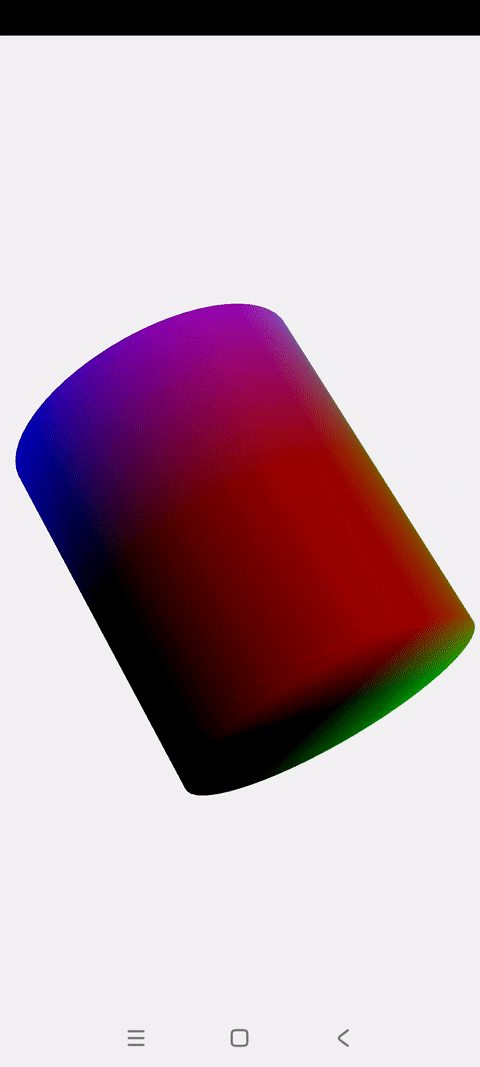
OpenGLES:绘制一个彩色、旋转的3D圆柱
一.概述 上一篇博文讲解了怎么绘制一个彩色旋转的立方体 这一篇讲解怎么绘制一个彩色旋转的圆柱 圆柱的顶点创建主要基于2D圆进行扩展,与立方体没有相似之处 圆柱绘制的关键点就是将圆柱拆解成:两个Z坐标不为0的圆 一个长方形的圆柱面 绘制2D圆的…...
【QT开发(6)】0926-QT 中加入 fastDDS 通信库的程序使用说明
在智能驾驶中,DDS有可能被广泛使用,因此推出这篇说明教程。 1、基于【QT开发(5)】教程的项目文档进行开发 2、安装DDS 查看《【eProsima Fast DDS(1)】安装eProsima Fast DDS》 至少安装: foonathan_m…...

js 判断字符串中是否包含某个字符串
方法一(推荐使用): indexOf() indexOf() 方法:返回某个指定的字符串值在字符串中首次出现的位置。如果要检索的字符串值没有出现,则该方法返回 -1。 var str "LiHeErNAN"; console.log(str.indexOf("A") ! -1 ); // true方法二:m…...

部署在阿里云ECS服务器上的微服务项目中获取到的时间和windows的时间不一样的问题
继上一篇文章《阿里云ECS服务器无法发送邮件问题解决方案》之后,又发现登录的时候发送邮件中的时间和自己windows上的时间不一样,大概找了一下原因,是LocaDateTime使用的时区不一样导致的远程服务器和本机时间不一致。 只需要在LocaDateTime…...
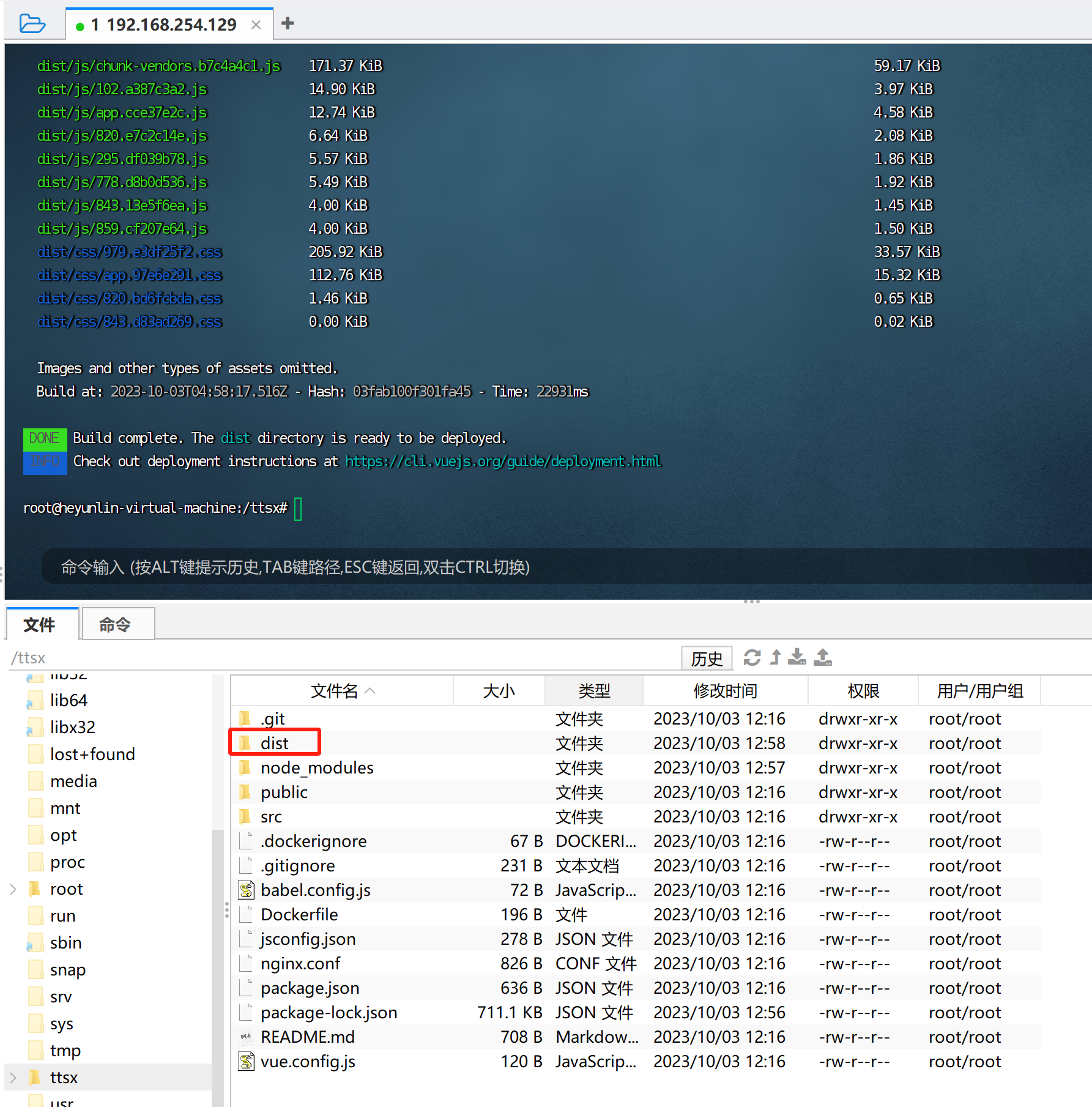
怎么通过portainer部署一个vue项目
这篇文章分享一下今天通过docker打包vue项目,并使用打包的镜像在portainer上部署运行,参考了vue-cli和docker的官方文档。 首先,阅读vue-cli关于docker部署的说明 vue-cli关于docker部署的说明https://cli.vuejs.org/guide/deployment.html#…...
)
Springboot实现websocket(连接前jwt验证token)
背景 用户连接服务器weksocket前,需经过jwt的token验证(token中包含账号信息),验证合法后,才可以于服务器正常交互。 实现 一、配置依赖(pom.xml) <!-- websocket --><dependency&g…...

2023/10/3
平荒尽处是春山 二零二三年的十月 似乎已经过去了很久很久 没有了曾经的意气风发 也没有了歌伴夜声 之前一直不知道自己为什么喜欢打篮球 虽然打得不好 但是今天突然明白了 我喜欢的不是过人后的喜悦 而是篮球应声入网的清脆的声音 当然 出来进球 还有的是擦筐而出和三不沾 但是…...
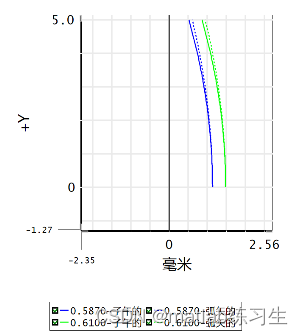
zemax场曲/畸变图与网格畸变图
网格畸变是XY两个方向上的几何畸变,是不同视场实际像高与近轴像高的偏差。 垂轴放大率在整个视场范围内不能保持常数 当一个有畸变的光学系统对一个方形的网状物体成像时,若δy>0,则主光线的交点高度y比理想像高y低,视场越大,低得越多&a…...

【小尘送书-第六期】《巧用ChatGPT轻松玩转新媒体运营》AI赋能运营全流程,帮你弯道超车、轻松攀登运营之巅
大家好,我是小尘,欢迎你的关注!大家可以一起交流学习!欢迎大家在CSDN后台私信我!一起讨论学习,讨论如何找到满意的工作! 👨💻博主主页:小尘要自信 …...
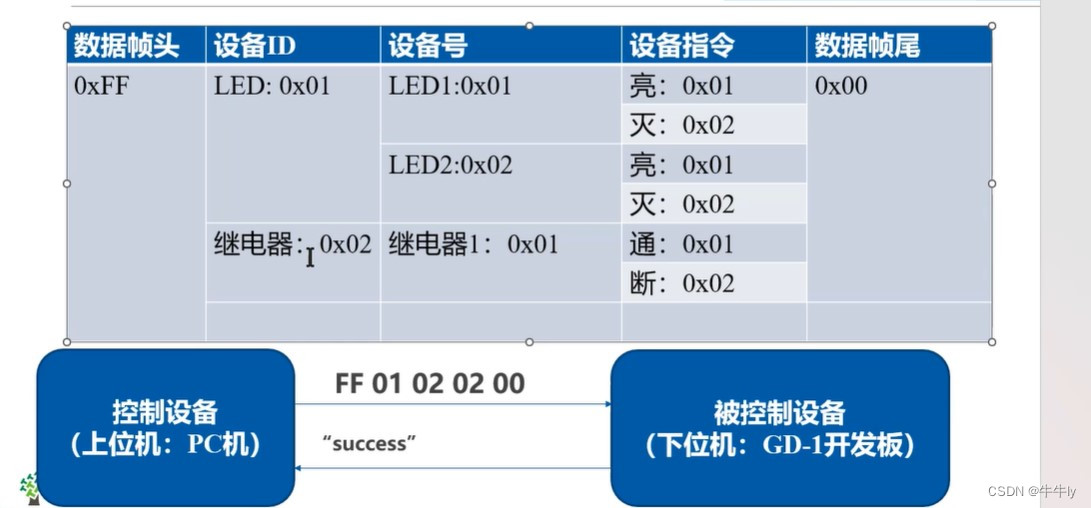
GD32F10 串口通信
1. 什么是通信 通信,指人与人或人与自然之间通过某种行为或媒介进行的信息交流与传递,从广义上指需要信息的双方或多方在不违背各自意愿的情况下采用任意方法,任意媒质,将信息从某方准确安全地传送到另方。通信双方如果想正确传输…...
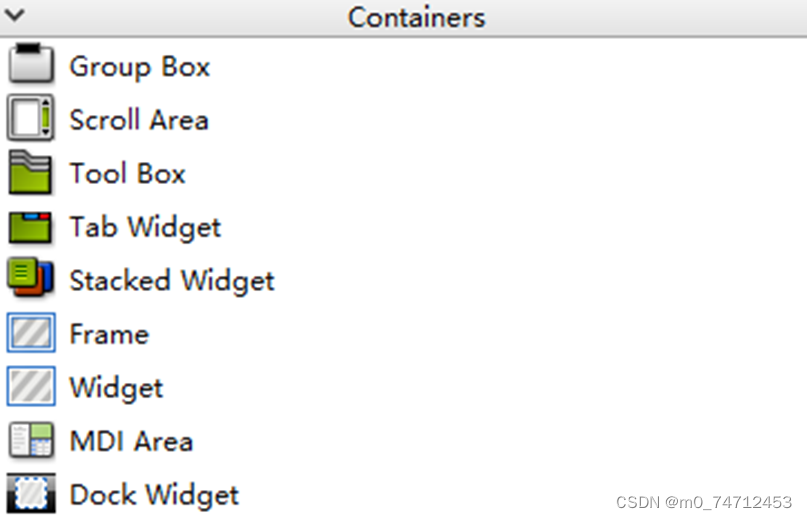
QT常用控件介绍
QT信号与槽机制 connect (A,SIGNLA(aaa()),B, SLOT(bbb())); GUI继承简介 布局管理器 垂直布局水平布局网格布局表单布局 输出控件 Label: 标签Text Browser: 文本浏览器Graphics View : 图形视图框架Calendar Widget: 日历控件LCD Number: 液晶字体数…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...

4. TypeScript 类型推断与类型组合
一、类型推断 (一) 什么是类型推断 TypeScript 的类型推断会根据变量、函数返回值、对象和数组的赋值和使用方式,自动确定它们的类型。 这一特性减少了显式类型注解的需要,在保持类型安全的同时简化了代码。通过分析上下文和初始值,TypeSc…...
