YoloV5实时推理最短的代码
YoloV5实时推理最简单代码
import cv2
import torch# 加载YOLOv5模型
model = torch.hub.load('ultralytics/yolov5', 'yolov5s')# 使用CPU或GPU进行推理
device = 'cuda' if torch.cuda.is_available() else 'cpu'
model.to(device)# 打开摄像头(默认摄像头)
cap = cv2.VideoCapture(0)while True:# 读取摄像头帧ret, frame = cap.read()if not ret:break# 进行推理results = model(frame)# 获取检测结果的图像output_img = results.render()[0]# 显示图像cv2.imshow('YOLOv5', output_img)# 检测键盘输入,按 'q' 键退出循环if cv2.waitKey(1) & 0xFF == ord('q'):break# 释放摄像头并关闭窗口
cap.release()
cv2.destroyAllWindows()- 导入必要的库:
cv2:OpenCV库,用于图像和视频处理。torch:PyTorch库,用于加载和运行YOLOv5模型。
- 加载YOLOv5模型:
- 使用
torch.hub.load函数从指定的GitHub仓库'ultralytics/yolov5'中加载YOLOv5模型'yolov5s'(小型版本)。模型将自动下载并加载。
- 使用
- 确定推理设备:
- 根据系统是否支持CUDA(GPU加速),选择在GPU(‘cuda’)或CPU(‘cpu’)上执行模型推理。
- 打开摄像头:
- 使用
cv2.VideoCapture打开默认的摄像头(通常是计算机内置摄像头或外部摄像头)。
- 使用
- 进入主循环:
- 使用
while True创建一个无限循环,以连续地从摄像头获取帧并进行目标检测。
- 使用
- 读取摄像头帧:
- 使用
cap.read()方法读取摄像头的下一帧图像。ret表示成功与否,frame包含捕获的图像。
- 使用
- 进行推理:
- 将读取的帧传递给YOLOv5模型进行目标检测,结果存储在
results中。
- 将读取的帧传递给YOLOv5模型进行目标检测,结果存储在
- 获取检测结果的图像:
- 使用
results.render()方法获取包含检测框和标签的图像,这里使用索引[0]表示获取第一帧的检测结果。
- 使用
- 显示图像:
- 使用
cv2.imshow()方法在名为’YOLOv5’的窗口中显示检测结果图像。
- 使用
- 检测键盘输入:
- 使用
cv2.waitKey(1)检测键盘输入,等待1毫秒。如果按下键盘上的 ‘q’ 键(ASCII码为0x71),则退出循环。
- 使用
- 释放摄像头并关闭窗口:
- 在循环结束后,释放摄像头资源(
cap.release())并关闭显示窗口(cv2.destroyAllWindows())。
- 在循环结束后,释放摄像头资源(

相关文章:

YoloV5实时推理最短的代码
YoloV5实时推理最简单代码 import cv2 import torch# 加载YOLOv5模型 model torch.hub.load(ultralytics/yolov5, yolov5s)# 使用CPU或GPU进行推理 device cuda if torch.cuda.is_available() else cpu model.to(device)# 打开摄像头(默认摄像头) cap…...
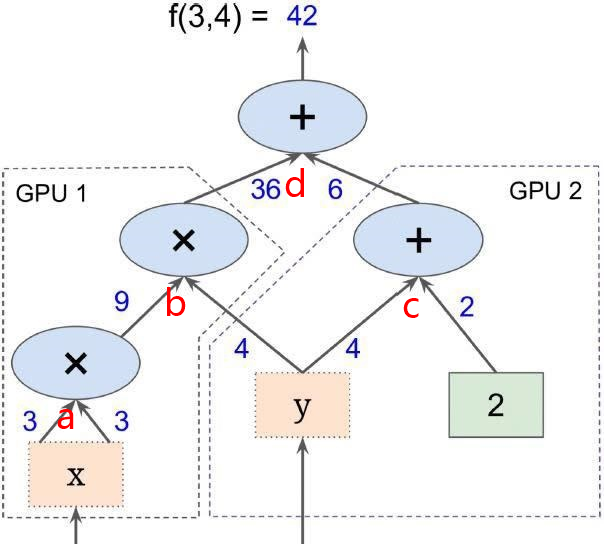
Tensorflow、Pytorch和Ray(张量,计算图)
1.深度学习框架(Tensorflow、Pytorch) 1.1由来 可以追溯到2016年,当年最著名的事件是alphago战胜人类围棋巅峰柯洁,在那之后,学界普遍认为人工智能已经可以在一些领域超过人类,未来也必将可以在更多领域超过…...

TinyWebServer学习笔记-让程序跑起来
目标:通过这个HTTP项目熟悉网络编程 系统:Ubuntu20.04 首先,学习的第一步就是先让程序跑起来,使用git将项目下载到虚拟机内: git clone https://github.com/qinguoyi/TinyWebServer.git 提前把MySQL数据库安装好&am…...

_tkinter.TclError: no display name and no $DISPLAY environment variable 解决
启动kohya_ss时可能会发生错误: _tkinter.TclError: no display name and no $DISPLAY environment variable 解决办法: 1、apt-get install xvfb //安装xvfb // 启动虚拟显示器 2、Xvfb :99 -screen 0 1024x768x16 & export DISPLAY:99 ps aux…...

我出手了!
时光飞逝,程序员小灰这个微信公众号,已经运营整整7年时间了。 在这7年里,小灰输出过各种各样的文章和视频,有讲编程技术的,有讲职业规划的,有讲互联网行业新闻的,也有讲自己个人生活的。 不过&a…...

springboot的配置文件(properties和yml/yaml)
springboot的配置文件有两种格式分别是properties和yml/yaml 创建配置文件 在创建springboot项目时候,会默认生成application.properties这种格式 书写风格 端口 application.propertis server.port8080 application.yml server:port: 8080 连接数据库 applica…...

SLAM面试笔记(7) — Linux面试题
目录 问题1:Linux系统基本组件? 问题2:Linux和Unix有什么区别? 问题3:Linux下编译程序 问题4:gcc基本格式和常用指令 问题5:用什么命令查找内存和交换使用情况? 问题6…...

QUIC不是TCP的替代品
QUIC取代了TCP成为HTTP3的基础传输协议,不是因为QUIC能够取代TCP的所有应用场景,而是因为QUIC更适合HTTP的请求/响应业务模型。原文: QUIC Is Not a TCP Replacement TCP新规范(RFC 9293)的发布是网络界的一件大事,值得围绕这一主题发表第二篇…...
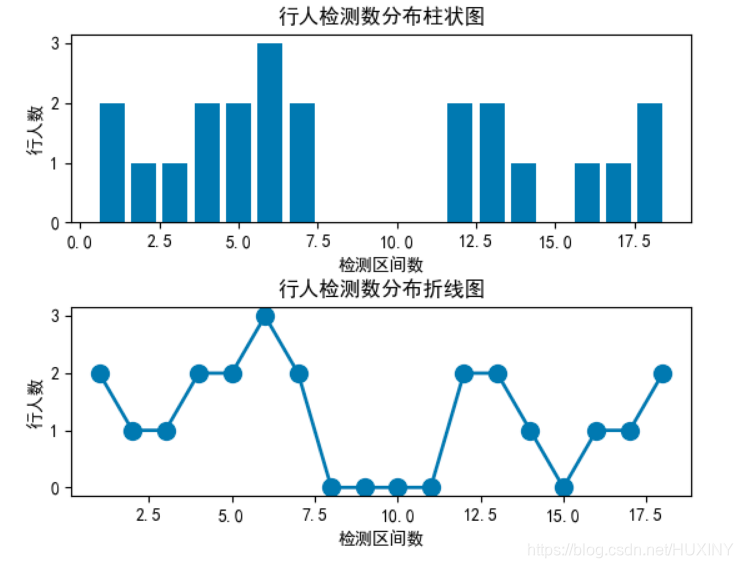
计算机竞赛 目标检测-行人车辆检测流量计数
文章目录 前言1\. 目标检测概况1.1 什么是目标检测?1.2 发展阶段 2\. 行人检测2.1 行人检测简介2.2 行人检测技术难点2.3 行人检测实现效果2.4 关键代码-训练过程 最后 前言 🔥 优质竞赛项目系列,今天要分享的是 行人车辆目标检测计数系统 …...
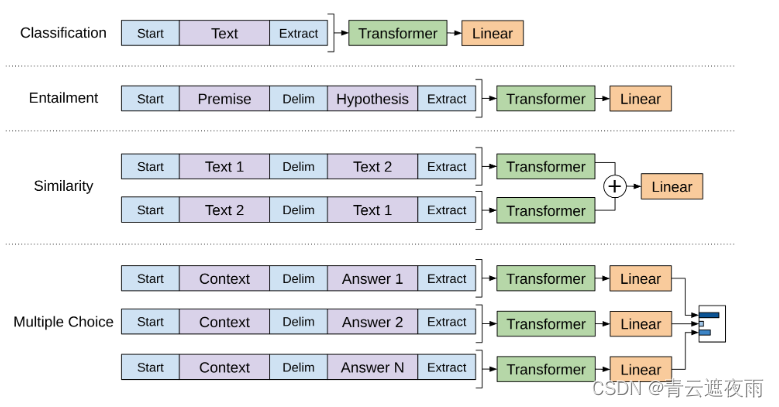
GPT系列模型解读:GPT-1
GPT系列 GPT(Generative Pre-trained Transformer)是一系列基于Transformer架构的预训练语言模型,由OpenAI开发。以下是GPT系列的主要模型: GPT:GPT-1是于2018年发布的第一个版本,它使用了12个Transformer…...

王杰国庆作业day3
父子进程对话 #include <stdio.h> #include <string.h> #include <stdlib.h> #include <my_head.h> int main(int argc, const char *argv[]) {mkfifo("./fifo1",0664);mkfifo("./fifo2",0664);pid_t cpid fork();if(0 < cp…...
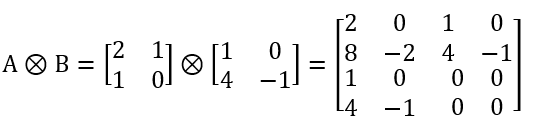
量子计算基础知识—Part1
1.什么是量子计算机? 量子计算机是基于量子力学原理构建的机器,采用了一种新的方法来处理信息,从而使其具有超强的功能。量子计算机使用Qubits处理信息。 2. 什么是量子系统? 一个量子系统指的是由量子力学规则描述和控制的物理…...

【PostgreSQL】【存储管理】表和元组的组织方式
外存管理负责处理数据库与外存介质(PostgreSQL8.4.1版本中只支持磁盘的管理操作)的交互过程。在PostgreSQL中,外存管理由SMGR(主要代码在smgr.c中)提供了对外存的统一接口。SMGR负责统管各种介质管理器,会根据上层的请求选择一个具体的介质管理器进行操作…...

VSCode安装图文详解教程
版权声明 本文原创作者:谷哥的小弟作者博客地址:http://blog.csdn.net/lfdfhl 教程说明 本教程旨在详细介绍VSCode的安装过程及其注意事项。 下载VSCode 请在官方网站 https://code.visualstudio.com/ 下载https://code.visualstudio.com/至本地&…...
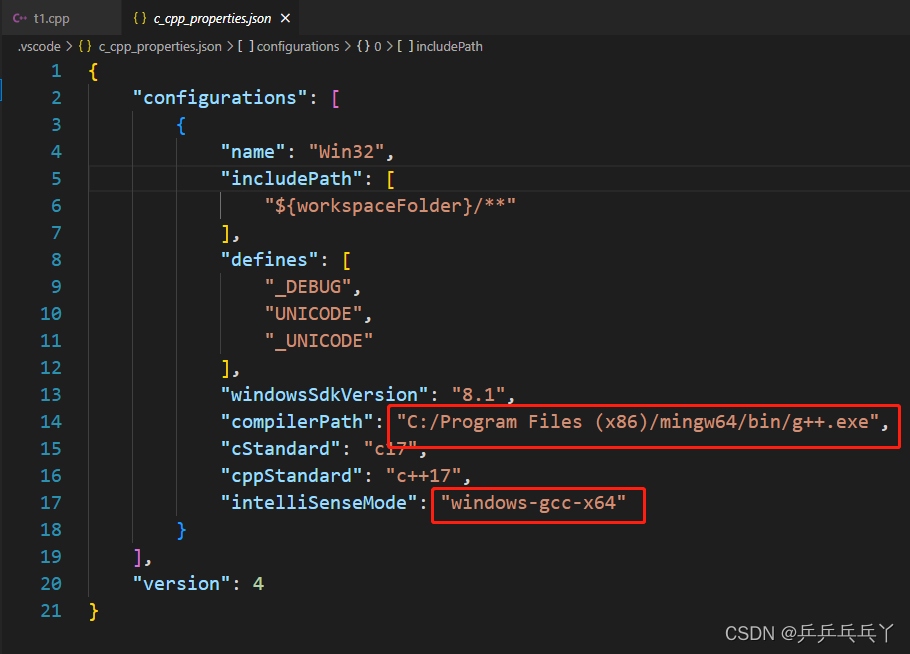
vscode 无法打开源文件
以下是c/c插件的intelligense设置情况: 解决办法: 重新安装vsode无用;重新下载mingw64,管用了!(我猜可能是之前换电脑移植文件的时候导致了部分文件丢失)...

1.8.C++项目:仿muduo库实现并发服务器之eventloop模块的设计
项目完整在: 文章目录 一、eventloop模块:进行事件监控,以及事件处理的模块二、提供的功能三、实现思想(一)功能(二)意义(三)功能设计 四、框架五、代码 一、eventloop模…...

Linux基本指令(二)
💓博主个人主页:不是笨小孩👀 ⏩专栏分类:数据结构与算法👀 C👀 刷题专栏👀 C语言👀 🚚代码仓库:笨小孩的代码库👀 ⏩社区:不是笨小孩👀 🌹欢迎大…...
)
量化交易全流程(五)
本节目录 策略回测 多因子模型 本节主要讨论回测相关的内容,包括两种不同的回测机制,即向量化回测和事件驱动回测;如何灵活使用开源工具来编写自己的回测程序;不同实现方式的优劣对比等。 在我们研究策略的时候,需要…...

聊聊MySQL的InnoDB引擎与MVCC
目录 一、InnoDB引擎 1.1逻辑存储结构 1). 表空间 2). 段 3). 区 4). 页 5). 行 1.2架构 1.2.1内存结构 1). Buffer Pool 2). Change Buffer 3). Adaptive Hash Index 4). Log Buffer 1.2.2磁盘结构 1). System Tablespace 2). File-Per-Table Tablespaces 3). …...
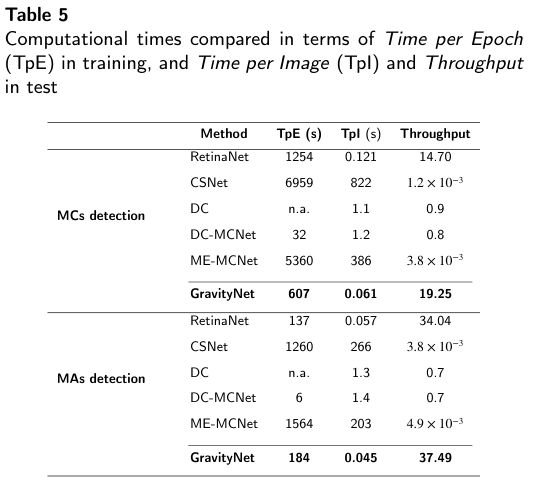
小病变检测:Gravity Network for end-to-end small lesion detection
论文作者:Ciro Russo,Alessandro Bria,Claudio Marrocco 作者单位:University of Cassino and L.M. 论文链接:http://arxiv.org/abs/2309.12876v1 内容简介: 1)方向:医学影像中小病变检测 2࿰…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...

【Redis】笔记|第8节|大厂高并发缓存架构实战与优化
缓存架构 代码结构 代码详情 功能点: 多级缓存,先查本地缓存,再查Redis,最后才查数据库热点数据重建逻辑使用分布式锁,二次查询更新缓存采用读写锁提升性能采用Redis的发布订阅机制通知所有实例更新本地缓存适用读多…...

实战三:开发网页端界面完成黑白视频转为彩色视频
一、需求描述 设计一个简单的视频上色应用,用户可以通过网页界面上传黑白视频,系统会自动将其转换为彩色视频。整个过程对用户来说非常简单直观,不需要了解技术细节。 效果图 二、实现思路 总体思路: 用户通过Gradio界面上…...

Java数组Arrays操作全攻略
Arrays类的概述 Java中的Arrays类位于java.util包中,提供了一系列静态方法用于操作数组(如排序、搜索、填充、比较等)。这些方法适用于基本类型数组和对象数组。 常用成员方法及代码示例 排序(sort) 对数组进行升序…...

echarts使用graphic强行给图增加一个边框(边框根据自己的图形大小设置)- 适用于无法使用dom的样式
pdf-lib https://blog.csdn.net/Shi_haoliu/article/details/148157624?spm1001.2014.3001.5501 为了完成在pdf中导出echarts图,如果边框加在dom上面,pdf-lib导出svg的时候并不会导出边框,所以只能在echarts图上面加边框 grid的边框是在图里…...
