算法通关村第五关-二叉树遍历(层数优先)之经典问题:简单的层序遍历、层序遍历分层、自底向上的层序遍历
基础知识(青铜挑战)
-
了解二叉树的基础知识
实战训练(白银挑战)
简单的层序遍历
-
基本的层序遍历思路很清晰:
-
给你一个二叉树根节点,你需要创建一个队列 queue 来遍历节点,一个链表 list 来存储节点的数据域,即值
-
首先将根节点入队
-
队列 queue 出队,将该节点值存入 list,再依次将左右孩子节点入队
-
重复以上操作,每个节点出对后,都存储该节点值到 list 中,再依次将左右孩子节点入队,直到队列 queue为空
-
这样得到的数据链表 list 就是按层序遍历的顺序得到的
-
-
具体代码如下:(2023/09/09午)
public static List<Integer> simpleLevelOrder(TreeNode root) {if (root == null) {return new ArrayList<Integer>();}
List<Integer> res = new ArrayList<Integer>();LinkedList<TreeNode> queue = new LinkedList<TreeNode>();//将根节点放入队列中,然后不断遍历队列queue.add(root);//有多少元素执行多少次while (queue.size() > 0) {//获取当前队列的长度,这个长度相当于 当前这一层的节点个数TreeNode t = queue.remove();res.add(t.val);if (t.left != null) {queue.add(t.left);}if (t.right != null) {queue.add(t.right);}}return res;}层序遍历分层
-
层序遍历我们做到了,这里添加一个要求:对层序遍历的节点值分层处理,即二叉树每层的节点值分别存放进一个链表 list 中
-
这个代码怎么写呢?很简单的,按这个思路走:
-
我们之前层序遍历时,每出队一个节点,都把其值存入 list 链表中,然后入队其孩子节点
-
在开始出队某一层的节点时,此时队列的节点数,就是二叉树这一层的节点数
-
那我们根据可以某时刻队列容量来遍历队列,将这层的节点全部出队,并且把节点值存入该层独有的 list 中
-
当然了,每个节点出队后,要将自己的孩子节点依次入队
-
这样,当队列为空时,我们得到了各层的节点链表 list,返回一个包含各层 list 的 list 即可
-
-
具体代码如下:(2023/09/09晚)
public static List<List<Integer>> level102Order(TreeNode root) {if (root == null) {return new ArrayList<List<Integer>>();}
List<List<Integer>> res = new ArrayList<List<Integer>>();LinkedList<TreeNode> queue = new LinkedList<TreeNode>();//将根节点放入队列中,然后不断遍历队列queue.add(root);while (queue.size() > 0) {//获取当前队列的长度,这个长度相当于 当前这一层的节点个数int size = queue.size();ArrayList<Integer> tmp = new ArrayList<Integer>();//将队列中的元素都拿出来(也就是获取这一层的节点),放到临时list中//如果节点的左/右子树不为空,也放入队列中for (int i = 0; i < size; ++i) {TreeNode t = queue.remove();tmp.add(t.val);if (t.left != null) {queue.add(t.left);}if (t.right != null) {queue.add(t.right);}}//将临时list加入最终返回结果中res.add(tmp);}return res;}自底向上的层序遍历
-
在前面学习的基础上,实现这个要求就很简单了
-
在拿到各层节点值的 list 后,按头插的方式,插入链表 list 中,就实现了自底向上的层序遍历了(2023/09/09晚)
-
具体代码如下:
public static List<List<Integer>> levelOrderBottom(TreeNode root) {List<List<Integer>> levelOrder = new LinkedList<List<Integer>>();if (root == null) {return levelOrder;}Queue<TreeNode> queue = new LinkedList<TreeNode>();queue.offer(root);while (!queue.isEmpty()) {List<Integer> level = new ArrayList<Integer>();int size = queue.size();for (int i = 0; i < size; i++) {TreeNode node = queue.poll();level.add(node.val);TreeNode left = node.left, right = node.right;if (left != null) {queue.offer(left);}if (right != null) {queue.offer(right);}}levelOrder.add(0, level);//栈}return levelOrder;}相关文章:
之经典问题:简单的层序遍历、层序遍历分层、自底向上的层序遍历)
算法通关村第五关-二叉树遍历(层数优先)之经典问题:简单的层序遍历、层序遍历分层、自底向上的层序遍历
基础知识(青铜挑战) 了解二叉树的基础知识 实战训练(白银挑战) 简单的层序遍历 基本的层序遍历思路很清晰: 给你一个二叉树根节点,你需要创建一个队列 queue 来遍历节点,一个链表 list 来存储…...

C++左右值及引用
1 左值和右值 简单记法:能取地址的是左值,不能取地址的是右值 右值一般是常量 例: i 是右值,因为先把 i 赋值给临时变量,临时变量在1,而临时变量是将亡值,&i取地址会报错 i是左值…...

如何备份和恢复数据库
目录 1.xtrabackup 是什么2.全量备份3.增量备份4.使用备份进行恢复5.原理6.参考 本文主要介绍如何使用xtrabackup 进行数据库的备份和恢复,并在最后介绍了原理。 1.xtrabackup 是什么 XtraBackup是由Percona开发的一款开源的MySQL数据库备份工具。它可以对InnoDB和…...

简化数据库操作:探索 Gorm 的约定优于配置原则
文章目录 使用 ID 作为主键数据库表名TableName临时指定表名列名时间戳自动填充CreatedAtUpdatedAt时间戳类型Gorm 采用约定优于配置的原则,提供了一些默认的命名规则和行为,简化开发者的操作。 使用 ID 作为主键 默认情况下,GORM 会使用 ID 作为表的主键: type User st…...
保姆级Anaconda安装教程
一.anaconda下载 建议使用清华大学开源软件镜像站进行下载,使用官网下载速度比较慢。 anaconda清华大学开源软件镜像站 : https://mirrors.tuna.tsinghua.edu.cn/anaconda/archive/ 一路next即可,注意添加环境变量得选项都勾上。 二.验证…...

你写过的最蠢的代码是?——后端篇
🌷🍁 博主猫头虎(🐅🐾)带您 Go to New World✨🍁 🦄 博客首页: 🐅🐾猫头虎的博客🎐《面试题大全专栏》 🦕 文章图文并茂🦖…...

快速幂
876. 快速幂求逆元 - AcWing题库 AC代码: #include <iostream> #include <cstring> #include <algorithm>using namespace std;typedef long long ll;int n;int qmi(int a,int k,int p) {int res1;while(k){if(k&1)res(ll)res*a%p;k>&…...

【题解 动态规划】 Colored Rectangles
题目描述: 分析: 乍一看我还以为是贪心! 猫 想想感觉没问题 但是局部最优并不能保证全局最优 比如这组数据 19 19 19 19 20 20 20 20如果按照贪心的做法,答案是20*20*2 但是其实答案是19*20*4 因此这道题用贪心是不对的 于是我…...
VsCode好用的扩展插件
开发插件推荐: 别名路径跳转 >> 点击引用的变量名,ctrl 点击 跳转文件Auto Rename Tag >> 修改标签前缀,后缀标签会同时修改Chinees 中文(简体)Code Runner >> 纯js文件右键点击run code即可底部终端打印file-icons-mac >> ma…...

Linux shell编程学习笔记4:修改命令行提示符格式(内容和颜色)
一、命令行提示符格式内容因shell类型而异 Linux终端命令行提示符内容格式则因shell的类型而异,例如CoreLinux默认的shell是sh,其命令行提示符为黑底白字,内容为: tcbox:/$ 其中,tc为当前用户名,box为主机…...

vue-引入使用main.js全局常量
common.js 命名什么都可以,用来定义常量的 定义了之后使用export让此暴露出去 const QRaddress http://localhost:9875export{QRaddress, } main.js //引入刚刚的js import {QRaddress} from /config/common.js挂载 Vue.prototype.$QRaddress QRaddress使用 …...
【C语言】【动态内存管理】malloc,free,calloc,realloc
1.malloc函数 void* malloc(size_t size)功能:向内存申请字节为 size大小的空间 使用时要包含头文件:<stdlib.h> 开辟成功:返回开辟好的空间初始地址的指针 开辟失败:返回空指针 NULL 使用举例: (malloc和free…...
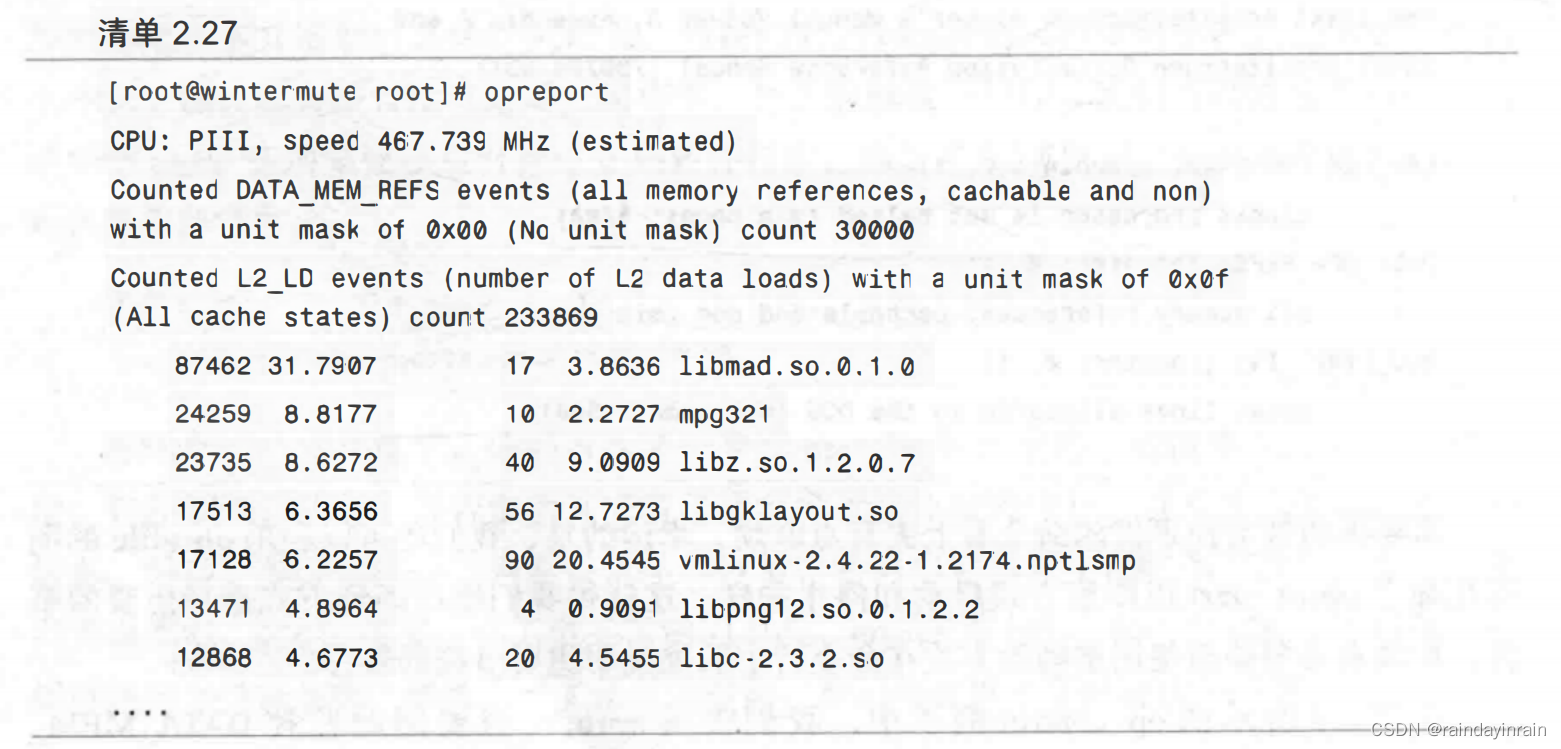
Linux性能优化--性能工具-系统CPU
2.0.概述 本章概述了系统级的Linux性能工具。这些工具是你追踪性能问题时的第一道防线。它们能展示整个系统的性能情况和哪些部分表现不好。 1.理解系统级性能的基本指标,包括CPU的使用情况。 2.明白哪些工具可以检索这些系统级性能指标。 2.1CPU性能统计信息 为…...

Ipython和Jupyter Notebook介绍
Ipython和Jupyter Notebook介绍 Python、IPython和Jupyter Notebook是三个不同但密切相关的工具。简而言之,Python是编程语言本身,IPython是对Python的增强版本,而Jupyter Notebook是一种在Web上进行交互式计算的环境,使用IPytho…...
)
数列极差(c++题解)
题目描述 佳佳的老师在黑板上写了一个由 n个正整数组成的数列,要求佳佳进行如下操作:每次擦去其中的两个数a 和b ,然后在数列中加入一个数a*b1 ,如此下去直至黑板上剩下一个数为止,在所有按这种操作方式最后得到的数…...
面试题:熟悉设计模式吗?谈谈简单工厂模式和策略模式的区别
刚刚接触设计模式的时候,我相信单例模式和工厂模式应该是用的最多的,毕竟很多的底层代码几乎都用了这些模式。自从接触了一次阿里的公众号发的一次文章关于 DDD的使用 以后,就逐渐接触了策略模式。现在在项目中运用最多的也是这几种设计模式了…...

Windows + Git + TortoiseGit + Github
一、下载Git(Git For Windows) 1.1. Git下载地址:https://gitforwindows.org/ 1.2. 默认安装即可(包名:Git-2.42.0.2-64-bit.exe) 二、下载TortoiseGit 2.1.TortoiseGit下载地址:http://tortoi…...

MySQL数据库索引练习
1.学生表:Student (Sno, Sname, Ssex , Sage, Sdept) 学号,姓名,性别,年龄,所在系 Sno为主键 课程表:Course (Cno, Cname,) 课程号,课程名 Cno为主键 学生选课表:SC (Sno, Cno, Scor…...

mysql面试题10:MySQL中有哪几种锁?表级锁、行级锁、页面锁区别和联系?
该文章专注于面试,面试只要回答关键点即可,不需要对框架有非常深入的回答,如果你想应付面试,是足够了,抓住关键点 面试官:Mysql中有哪几种锁? 在MySQL中,主要有以下几种类型的锁: 共享锁(Shared Lock):也称为读锁。多个事务可以同时持有共享锁,可以读取但不能修…...
ctfshow—1024系列练习
1024 柏拉图 有点像rce远程执行,有四个按钮,分别对应四份php文件,开始搞一下。一开始,先要试探出 文件上传到哪里? 怎么读取上传的文件? 第一步:试探上传文件位置 直接用burp抓包,…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...

macOS 终端智能代理检测
🧠 终端智能代理检测:自动判断是否需要设置代理访问 GitHub 在开发中,使用 GitHub 是非常常见的需求。但有时候我们会发现某些命令失败、插件无法更新,例如: fatal: unable to access https://github.com/ohmyzsh/oh…...

云安全与网络安全:核心区别与协同作用解析
在数字化转型的浪潮中,云安全与网络安全作为信息安全的两大支柱,常被混淆但本质不同。本文将从概念、责任分工、技术手段、威胁类型等维度深入解析两者的差异,并探讨它们的协同作用。 一、核心区别 定义与范围 网络安全:聚焦于保…...

链式法则中 复合函数的推导路径 多变量“信息传递路径”
非常好,我们将之前关于偏导数链式法则中不能“约掉”偏导符号的问题,统一使用 二重复合函数: z f ( u ( x , y ) , v ( x , y ) ) \boxed{z f(u(x,y),\ v(x,y))} zf(u(x,y), v(x,y)) 来全面说明。我们会展示其全微分形式(偏导…...
