利用t.ppft.interval分别计算T分布置信区间[实例]
scipy.stats.t.interval用于计算t分布的置信区间,即给定置信水平时,计算对应的置信区间的下限和上限。
scipy.stats.t.ppf用于计算t分布的百分位点,即给定百分位数(概率)时,该函数返回给定百分位数对应的t分布的值。//它的作用是根据给定的累积概率值,计算随机变量的值,使得该值以下的累积概率等于给定的概率。
利用t.ppf&t.interval分别计算T分布置信区间[实例]
import scipy.stats as stats
import numpy as np# 指定概率值(例如,95% 置信水平对应的概率)
alpha = 0.05# 指定样本数据
data = np.array([34,56,39,71,84,92,44,67,98,49,55,73,50,62,75,44,88,53,61,25,36,66,77,35])# 计算样本均值和标准误差
sample_mean = np.mean(data)
sample_std = np.std(data, ddof=1) # 使用ddof=1进行自由度校正
sample_size = len(data)
standard_error = sample_std / np.sqrt(sample_size)# 计算T分布的置信区间的上下限
t_critical = stats.t.ppf(1 - alpha / 2, df=sample_size - 1) # 自由度为样本大小减一
confidence_interval_lower = sample_mean - t_critical * standard_error
confidence_interval_upper = sample_mean + t_critical * standard_error# 输出T分布置信区间的上下限
print("T分布置信区间的下限:", confidence_interval_lower)
print("T分布置信区间的上限:", confidence_interval_upper)print("-------------------")
# 计算t分布的置信区间
t_confidence_interval = stats.t.interval(1 - alpha, df=sample_size - 1, loc=sample_mean, scale=sample_std / np.sqrt(sample_size))
# 输出计算结果
print("t分布的置信区间:", t_confidence_interval)# T分布置信区间的下限: 51.356996738889045
# T分布置信区间的上限: 68.14300326111095
# -------------------
# t分布的置信区间: (51.356996738889045, 68.14300326111095)
# [Finished in 5.1s]附录:多种方式进行T分布检验
import numpy as np
import scipy.stats as stats
import matplotlib.pyplot as plt# 创建一个样本数据,假设它符合T分布
np.random.seed(0)
sample_data = np.random.standard_t(df=5, size=100)# 绘制直方图
plt.hist(sample_data, bins=20, density=True, alpha=0.6, color='b', label='Histogram')# 绘制T分布的概率密度函数(PDF)曲线
x = np.linspace(min(sample_data), max(sample_data), 100)
pdf = stats.t.pdf(x, df=5)
plt.plot(x, pdf, 'r-', lw=2, label='T-Distribution PDF')# 添加图例和标签
plt.legend()
plt.title('Histogram and PDF of Sample Data')
plt.xlabel('Value')
plt.ylabel('Probability Density')# 显示图形
plt.show()# 绘制Q-Q图
stats.probplot(sample_data, dist="t", sparams=(5,), plot=plt)
plt.title('Q-Q Plot against T-Distribution')# 显示Q-Q图
plt.show()# 进行正态性检验(Shapiro-Wilk检验)
shapiro_test_statistic, shapiro_p_value = stats.shapiro(sample_data)
print("Shapiro-Wilk检验统计量:", shapiro_test_statistic)
print("Shapiro-Wilk检验p值:", shapiro_p_value)相关文章:

利用t.ppft.interval分别计算T分布置信区间[实例]
scipy.stats.t.interval用于计算t分布的置信区间,即给定置信水平时,计算对应的置信区间的下限和上限。 scipy.stats.t.ppf用于计算t分布的百分位点,即给定百分位数(概率)时,该函数返回给定百分位数对应的t…...
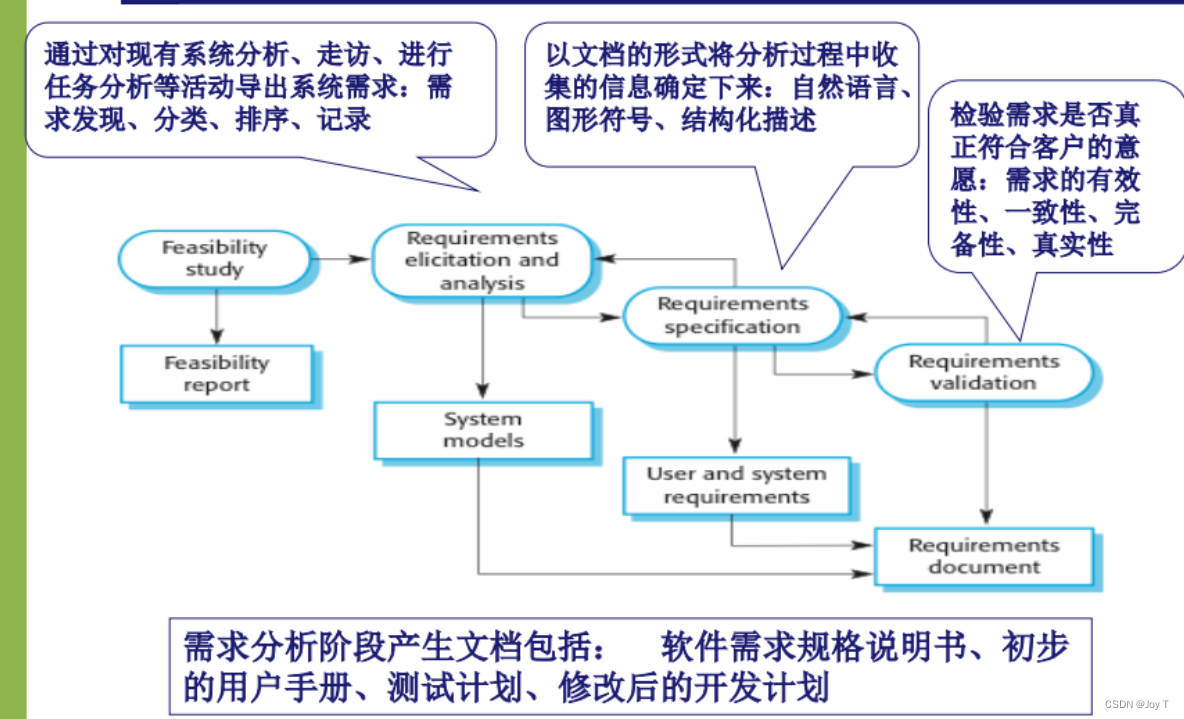
软件工程第三周
可行性研究 续 表达工作量的方式 LOC估算:Line of Code 估算公式S(Sopt4SmSpess)/6 FP:功能点 1. LOC (Line of Code) 估算 定义:LOC是指一个软件项目中的代码行数。 2. FP (Function Points) 估算 定义:FP是基于软件的功能性和…...
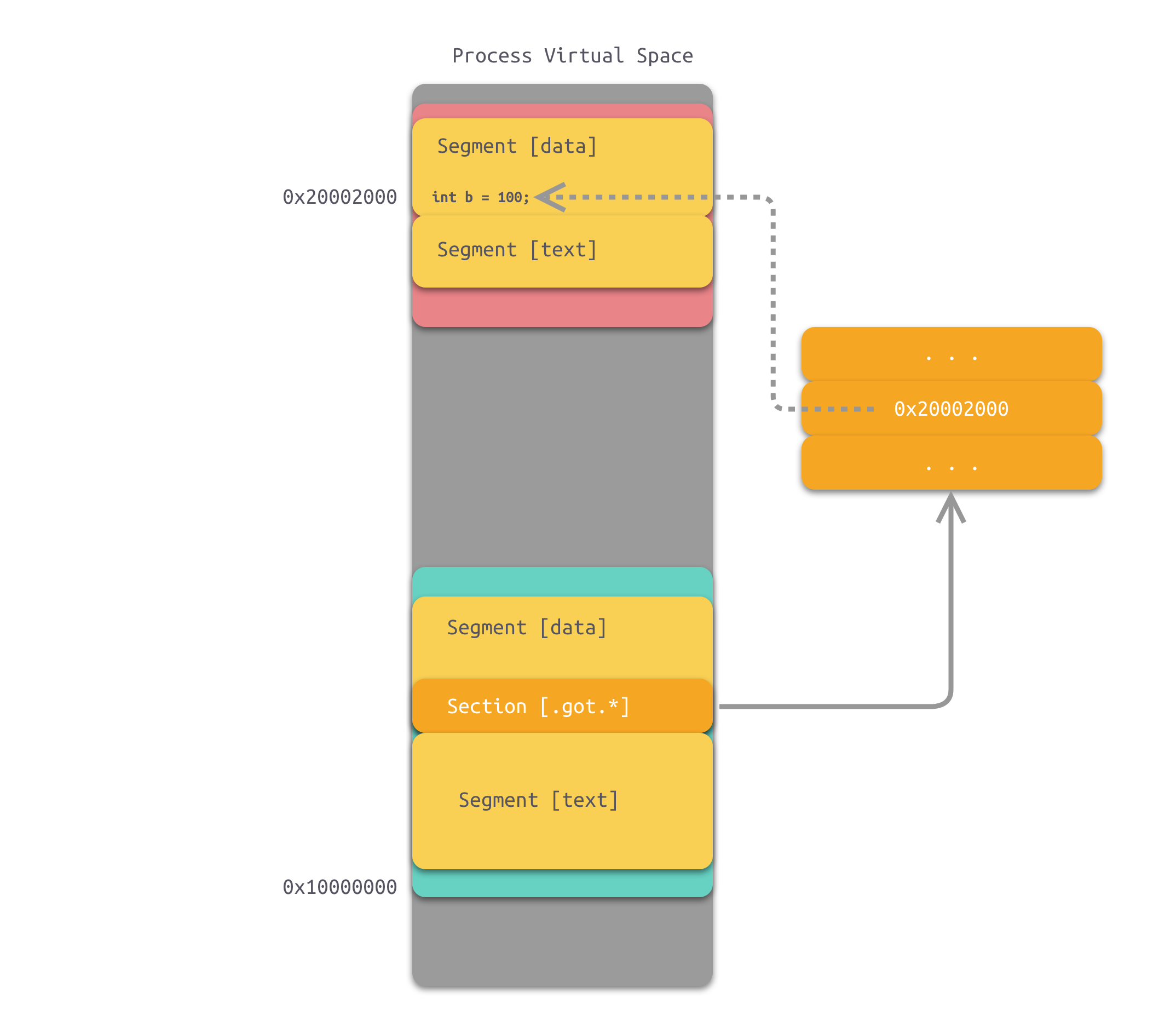
动态链接那些事
1、为什么要动态链接 1.1 空间浪费 对于静态链接来说,在程序运行之前,会将程序所需的所有模块编译、链接成一个可执行文件。这种情况下,如果 Program1 和 Program2 都需要用到 Lib.o 模块,那么,内存中和磁盘中实际上就…...

力扣:118. 杨辉三角(Python3)
题目: 给定一个非负整数 numRows,生成「杨辉三角」的前 numRows 行。 在「杨辉三角」中,每个数是它左上方和右上方的数的和。 来源:力扣(LeetCode) 链接:力扣(LeetCode)官…...

QGIS文章二——DEM高程裁剪和3D地形图
经常看到别人基于高程文件制作出精美的3D地图,笔者按照互联网几种制作方式进行尝试后,写的DEM高程裁剪和3D地形图教程,或许其中有一些错误的,也请指出。 本文基于海南省的shp文件和海南省DEM高程文件,制作海口地区的3D…...

【kubernetes】kubernetes中的StatefulSet使用
TOC 1 为什么需要StatefulSet 常规的应用通常使用Deployment,如果需要在所有机器上部署则使用DaemonSet,但是有这样一类应用,它们在运行时需要存储一些数据,并且当Pod在其它节点上重建时也希望这些数据能够在重建后的Pod上获取&…...

创建文件夹
/storage/emulated/0/代码文件/ 没有就创建 文件名命名方法:编号. 库 时间戳 使用Python的os模块来检查目录是否存在,并在不存在时创建它。下面是一个示例代码,演示了如何检查指定路径下的目录是否存在,若不存在则创建…...

点击router-link时候会发生什么?
当你点击链接或按钮时,将会导航到 User 组件,就会显示相应的用户 ID。 这里说一下执行流程,当点击一个 router-link 时,Vue Router会执行以下流程: 1)点击事件触发: 当你点击 router-link 组件时…...

【Spring】@Bean方法中存在继承如何分析
文章目录 1. 提问:如果让您分析Spring MVC的原理,您如何开始分析呢2. 如何破局3. 资料参考 本文主要介绍:如何分析 Bean方法存在继承 或 Bean方法中存在调用子类方法。 1. 提问:如果让您分析Spring MVC的原理,您如何…...

【Vim 插件管理器】Vim-plug和Vim-vbundle的区别
- vundle是一款老款的插件管理工具 - vim-plug相对较新,特点是支持异步加载,相比vundle而言 Vim-plug 是一个自由、开源、速度非常快的、极简的 vim 插件管理器。它可以并行地安装或更新插件。你还可以回滚更新。它创建浅层克隆shallow clone最小化磁盘…...

电子计算机核心发展(继电器-真空管-晶体管)
目录 继电器 最大的机电计算机之一——哈弗Mark1号,IBM1944年 背景 组成 性能 核心——继电器 简介 缺点 速度 齿轮磨损 Bug的由来 真空管诞生 组成 控制开关电流 继电器对比 磨损 速度 缺点 影响 代表 第一个可编程计算机 第一个真正通用&am…...
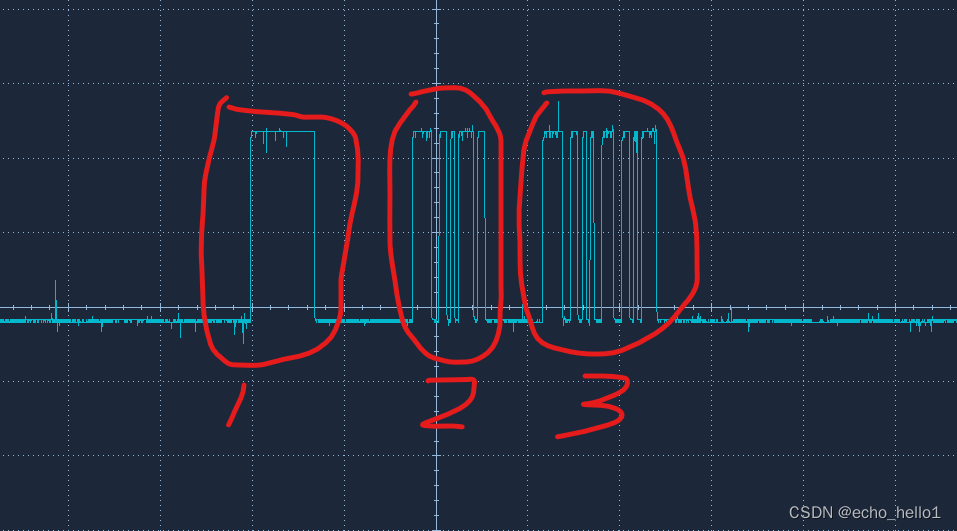
SDI-12协议与STM32 进行uart通信
场景是用stm32与一款温湿度传感器通信,不过是基于SDI-12协议,SDI-12时序和UART类似,故采用UART传输,原理图如下 其中DIR_OUT_SDI是一个IO引脚,控制UART_TX_SDI是否使能,U10是三态门IC,即拉低DIR…...

JS中的强制类型转换
JavaScript 中有多种强制类型转换的方式,可以将一个数据类型转换为另一种数据类型。这可以通过一些内置函数或操作符来实现。 显式类型转换(强制类型转换): 显式类型转换是通过特定的函数或操作符来明确指定要进行的类型转换。以下…...
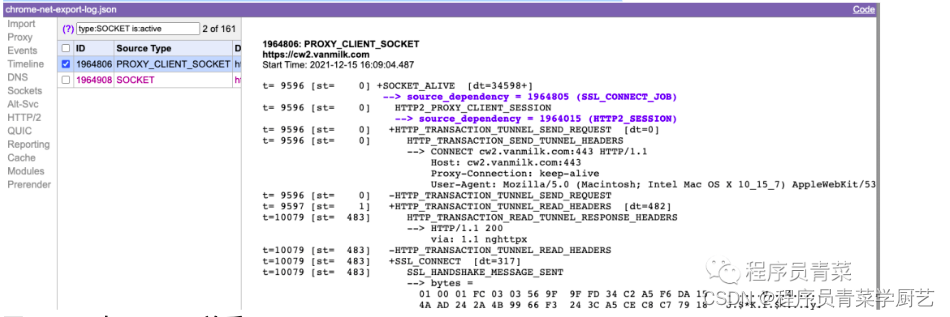
WebSocket实战之四WSS配置
一、前言 上一篇文章WebSocket实战之三遇上PAC ,碰到的问题只能上安全的WebSocket(WSS)才能解决,配置证书还是挺麻烦的,主要是每年都需要重新更新证书,我配置过的证书最长有效期也只有两年,搞不…...
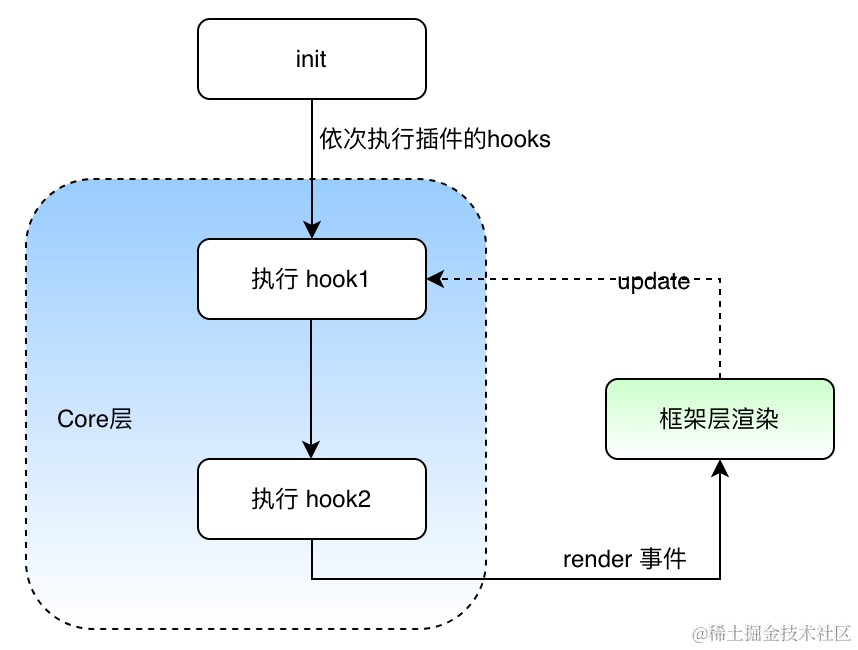
veImageX 演进之路:Web 图片加载提速50%
背景说明 火山引擎veImageX演进之路主要介绍了veImageX在字节内部从2012年随着字节成长过程中逐步演进的过程,演进中包括V1、V2、V3版本并最终面向行业输出;整个演进过程中包括服务端、客户端、网络库、业务场景与优化等多个角度介绍在图像处理压缩、省成…...
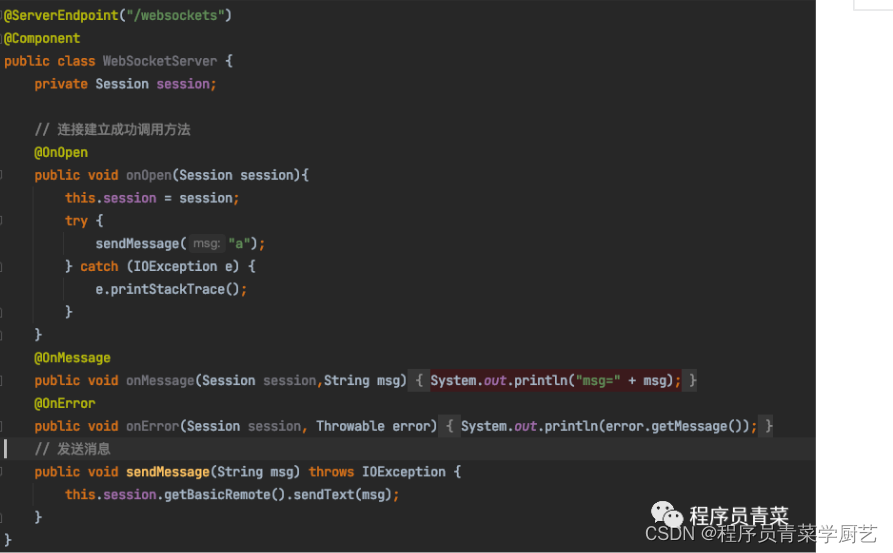
WebSocket实战之五JSR356
一、前言 前几篇WebSocket例子服务端我是用NodeJS实现,这一篇我们用Java来搭建一个WebSocket服务端,从2011年WebSocket协议RFC6455发布后,大多数浏览器都实现了WebSocket协议客户端的API,而对于服务端Java也定义了一个规范JSR356,即Java API for WebSoc…...

flask-sqlalchemy结合Blueprint遇到循环引入问题的解决方案
想要用flask_sqlalchemy结合Blueprint分模块写一下SQL的增删改查接口,结果发现有循环引入问题。 一开始,我在app.py中使用db SQLAlchemy(app)创建数据库对象;并且使用app.register_blueprint(db_bp, url_prefix/db)注册蓝图。 这使得我的依…...
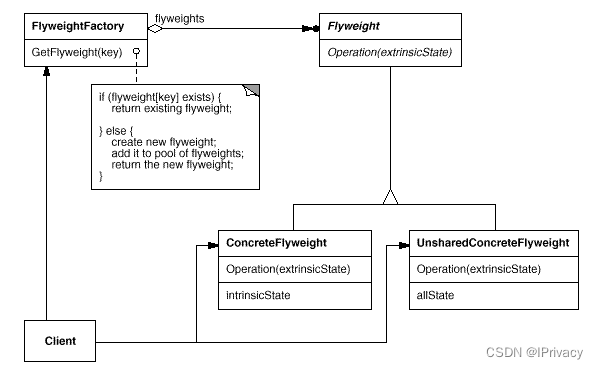
05_对象性能模式
对象性能模式 面向对象很好地解决了“抽象”的问题,但是必不可免地要付出定的代价。对于通常情况来讲,面向对象的成本大都可以忽略计。但是某些情况,面向对象所带来的成本必须谨慎处理。 典型模型: SingletonFlyweight Singleton 单件模式…...

快速选择排序
"你经过我每个灿烂时刻,我才真正学会如你般自由" 前些天有些无聊,想试试自己写的快排能否过leetcode上的排序算法题。结果是,不用截图可想而知,肯定是没过的,否则也不会有这篇文章的产出。 这份快排算法代码…...

国庆中秋特辑(六)大学生常见30道宝藏编程面试题
以下是 30 道大学生 Java 面试常见编程面试题和答案,包含完整代码: 什么是 Java 中的 main 方法? 答:main 方法是 Java 程序的入口点。它是一个特殊的方法,不需要被声明。当 Java 运行时系统执行一个 Java 程序时&…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...

视觉slam--框架
视觉里程计的框架 传感器 VO--front end VO的缺点 后端--back end 后端对什么数据进行优化 利用什么数据进行优化的 后端是怎么进行优化的 回环检测 建图 建图是指构建地图的过程。 构建的地图是点云地图还是什么信息的地图? 建图并没有一个固定的形式和算法…...

盲盒一番赏小程序:引领盲盒新潮流
在盲盒市场日益火爆的今天,如何才能在众多盲盒产品中脱颖而出?盲盒一番赏小程序给出了答案,它以创新的玩法和优质的服务,引领着盲盒新潮流。 一番赏小程序的最大特色在于其独特的赏品分级制度。赏品分为多个等级,从普…...

Modbus转ETHERNET IP网关:快速冷却系统的智能化升级密钥
现代工业自动化系统中,无锡耐特森Modbus转Ethernet IP网关MCN-EN3001扮演着至关重要的角色。通过这一技术,传统的串行通讯协议Modbus得以在更高速、更稳定的以太网环境中运行,为快速冷却系统等关键设施的自动化控制提供了强有力的支撑。快速冷…...

详解ZYNQ中的 RC 和 EP
详解ZYNQ中的 RC 和 EP 一、ZYNQ FPGA 开发板基础( ZC706 ) 1. 核心特点 双核大脑 灵活积木: ZC706 集成了 ARM Cortex-A9 双核处理器(相当于电脑 CPU)和 FPGA 可编程逻辑单元(相当于可自定义的硬件积木…...

设计模式-观察着模式
观察者模式 观察者模式 (Observer Pattern) 是一种行为型设计模式,它定义了对象之间一种一对多的依赖关系,当一个对象(称为主题或可观察者)的状态发生改变时,所有依赖于它的对象(称为观察者)都…...

FMC STM32H7 SDRAM
如何无痛使用片外SDRAM? stm32 已经成功初始化了 STM32H7 上的外部 SDRAM(32MB) 如何在开发中无痛使用SDRAM 使它像普通 RAM 一样“自然地”使用? [todo] 重要 MMT(Memory Management Tool) of STM32CubeMx The Memory Management Tool (MMT) disp…...
