【算法基础】一文掌握十大排序算法,冒泡排序、插入排序、选择排序、归并排序、计数排序、基数排序、希尔排序和堆排序
目录
1 冒泡排序(Bubble Sort)
2 插入排序(Insertion Sort)
3 选择排序(Selection Sort)
4. 快速排序(Quick Sort)
5. 归并排序(Merge Sort)
6 堆排序 (Heap Sort)
7 计数排序 (Counting Sort)
8 基数排序 (Radix Sort)
9 希尔排序(Shell Sort)
10 桶排序
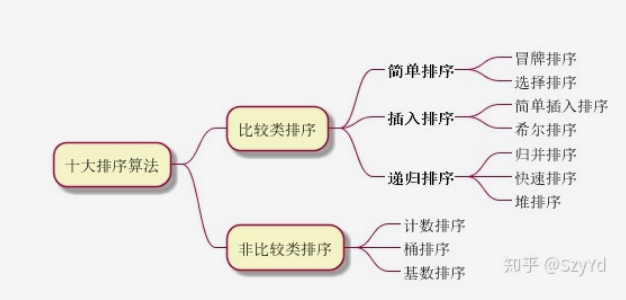
1 冒泡排序(Bubble Sort)
冒泡排序是一种基本的排序算法,其核心思想是多次遍历待排序的元素,比较相邻的两个元素,如果它们的顺序不正确,则交换它们,直到整个数组按照指定顺序排列。
def bubble_sort(arr):n = len(arr)for i in range(n):for j in range(0, n-i-1):# 比较相邻的两个元素if arr[j] > arr[j+1]:# 如果顺序不正确,则交换它们arr[j], arr[j+1] = arr[j+1], arr[j]# 示例用法
arr = [64, 34, 25, 12, 22, 11, 90]
bubble_sort(arr)
print("冒泡排序后的数组:", arr)
冒泡排序通过多次遍历数组,每次比较相邻的两个元素,如果它们的顺序不正确就交换它们。这个过程将最大的元素逐渐“冒泡”到数组的末尾。
时间复杂度为 O(n^2),不适合大规模数据集。
2 插入排序(Insertion Sort)
插入排序是一种稳定的排序算法,其核心思想是将未排序的元素逐个插入到已排序的部分,从前往后遍历,保持前面的元素有序。
def insertion_sort(arr):for i in range(1, len(arr)):key = arr[i]j = i - 1while j >= 0 and key < arr[j]:# 将较大的元素向右移动arr[j + 1] = arr[j]j -= 1arr[j + 1] = key# 示例用法
arr = [64, 34, 25, 12, 22, 11, 90]
insertion_sort(arr)
print("插入排序后的数组:", arr)
插入排序逐个将未排序的元素插入到已排序的部分,从前往后遍历,保持前面的元素有序。时间复杂度为 O(n^2),适合小规模数据集和部分有序的数据。
3 选择排序(Selection Sort)
选择排序是一种简单的不稳定排序算法,其核心思想是找到未排序部分的最小元素,将其与未排序部分的第一个元素交换位置。
def selection_sort(arr):n = len(arr)for i in range(n):min_index = ifor j in range(i+1, n):# 找到未排序部分的最小元素的索引if arr[j] < arr[min_index]:min_index = j# 交换最小元素与未排序部分的第一个元素arr[i], arr[min_index] = arr[min_index], arr[i]# 示例用法
arr = [64, 34, 25, 12, 22, 11, 90]
selection_sort(arr)
print("选择排序后的数组:", arr)
选择排序通过多次选择未排序部分的最小元素,并将其与未排序部分的第一个元素交换位置来进行排序。时间复杂度为 O(n^2),不适合大规模数据集。
4. 快速排序(Quick Sort)
快速排序是一种高效的分治排序算法,它选择一个基准元素,将数组分成两部分,左边的元素都小于基准,右边的元素都大于基准,然后递归对左右两部分进行排序。
def quick_sort(arr):# 基本情况:如果数组为空或只包含一个元素,无需排序if len(arr) <= 1:return arr# 选择中间元素作为基准点(pivot)pivot = arr[len(arr) // 2]# 将数组分成三部分:小于、等于、大于基准点的元素left = [x for x in arr if x < pivot]middle = [x for x in arr if x == pivot]right = [x for x in arr if x > pivot]# 递归排序左右两部分,然后合并结果return quick_sort(left) + middle + quick_sort(right)# 示例用法
arr = [64, 34, 25, 12, 22, 11, 90]
arr = quick_sort(arr)
print("快速排序后的数组:", arr)
- 快速排序是一种高效的分治排序算法,它通过选择一个基准点(通常是数组中的中间元素)将数组分成左右两部分,并递归地对左右两部分进行排序。
- 基本情况是数组为空或只包含一个元素,无需排序。
- 针对每个元素,将它与基准点进行比较,分成小于、等于和大于基准点的三个子数组。
- 然后,递归地对左右两部分进行排序,最后将它们与基准点合并,形成一个有序的数组。
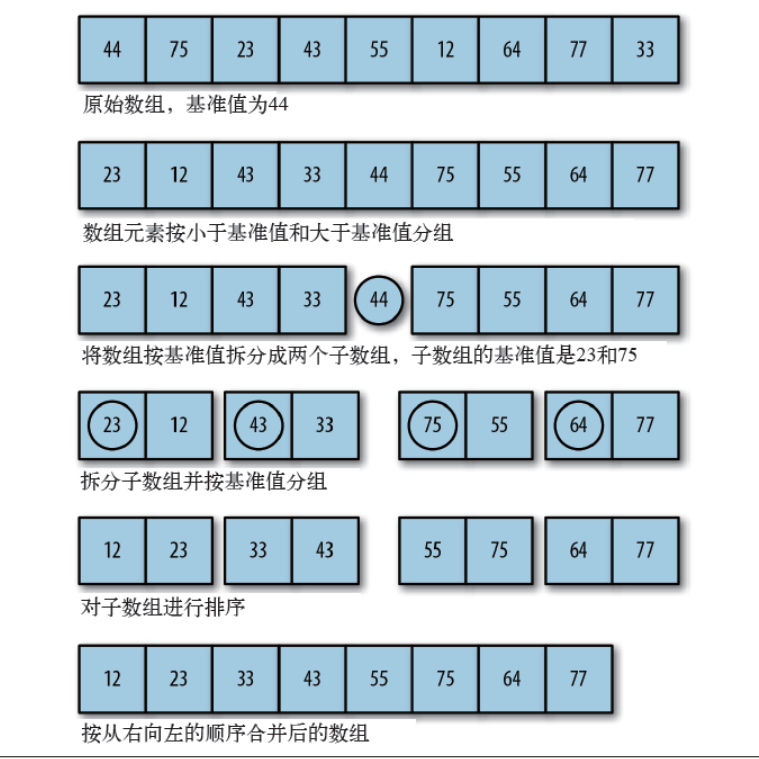
5. 归并排序(Merge Sort)
归并排序是一种稳定的分治排序算法,它将数组分成两半,分别排序,然后将已排序的两个子数组合并成一个有序数组。
def merge_sort(arr):# 基本情况:如果数组为空或只包含一个元素,无需排序if len(arr) <= 1:return arr# 将数组分成两半mid = len(arr) // 2left = arr[:mid]right = arr[mid:]# 递归地对左右两部分进行排序left = merge_sort(left)right = merge_sort(right)# 合并已排序的左右两部分return merge(left, right)def merge(left, right):result = []i = j = 0# 合并两个已排序的子数组while i < len(left) and j < len(right):if left[i] < right[j]:result.append(left[i])i += 1else:result.append(right[j])j += 1# 如果左边或右边的子数组还有剩余元素,将它们添加到结果中result.extend(left[i:])result.extend(right[j:])return result# 示例用法
arr = [64, 34, 25, 12, 22, 11, 90]
arr = merge_sort(arr)
print("归并排序后的数组:", arr)
- 归并排序是一种稳定的分治排序算法,它将数组递归分成两半,然后合并已排序的子数组。
- 基本情况是数组为空或只包含一个元素,无需排序。
- 递归地对左右两部分进行排序,然后使用
merge函数将它们合并成一个有序的数组。merge函数将两个已排序的子数组合并,同时维护它们的有序性。
6 堆排序 (Heap Sort)
堆排序是一种不稳定的排序算法,它使用堆数据结构(通常是最大堆)来进行排序。堆排序分为两个主要步骤:建立堆和排序。
def heapify(arr, n, i):largest = ileft = 2 * i + 1right = 2 * i + 2# 找到左子节点和右子节点中的最大值if left < n and arr[left] > arr[largest]:largest = leftif right < n and arr[right] > arr[largest]:largest = right# 如果最大值不是当前节点,交换它们if largest != i:arr[i], arr[largest] = arr[largest], arr[i]def heap_sort(arr):n = len(arr)# 构建最大堆for i in range(n // 2 - 1, -1, -1):heapify(arr, n, i)# 一个接一个地从堆中取出元素,交换根节点与最后一个节点,然后重新构建堆for i in range(n - 1, 0, -1):arr[i], arr[0] = arr[0], arr[i]heapify(arr, i, 0)# 示例用法
arr = [64, 34, 25, 12, 22, 11, 90]
heap_sort(arr)
print("堆排序后的数组:", arr)
- 排序使用堆数据结构(通常是最大堆)来进行排序。首先构建最大堆,然后一个接一个地从堆中取出元素,交换根节点与最后一个节点,然后重新构建堆。
heapify函数用于维护堆的性质,即父节点的值大于或等于子节点的值。- 这个算法的时间复杂度为 O(nlogn),是一种高效的排序算法。
7 计数排序 (Counting Sort)
计数排序是一种非比较排序算法,它根据输入元素的计数来对元素进行排序。它适用于整数或有限范围内的非负整数。
def counting_sort(arr):max_val = max(arr)min_val = min(arr)range_of_elements = max_val - min_val + 1count_arr = [0] * range_of_elementsoutput_arr = [0] * len(arr)# 计数每个元素的出现次数for num in arr:count_arr[num - min_val] += 1# 计算每个元素的累积计数for i in range(1, len(count_arr)):count_arr[i] += count_arr[i - 1]# 根据累积计数将元素放入输出数组for i in range(len(arr) - 1, -1, -1):output_arr[count_arr[arr[i] - min_val] - 1] = arr[i]count_arr[arr[i] - min_val] -= 1return output_arr# 示例用法
arr = [4, 2, 2, 8, 3, 3, 1]
arr = counting_sort(arr)
print("计数排序后的数组:", arr)
- 计数排序是一种非比较排序算法,适用于整数或有限范围内的非负整数。
- 首先,计算每个元素的出现次数,然后计算每个元素的累积计数,最后根据累积计数将元素放入输出数组。
- 这个算法的时间复杂度为 O(n+k),其中 k 是输入范围的大小。
8 基数排序 (Radix Sort)
基数排序是一种非比较排序算法,它将数字按照每个位数进行排序,从最低位到最高位,依次排列。
def counting_sort(arr, exp):n = len(arr)output = [0] * ncount = [0] * 10# 计数每个元素的出现次数for i in range(n):index = arr[i] // expcount[index % 10] += 1# 计算每个元素的累积计数for i in range(1, 10):count[i] += count[i - 1]# 根据累积计数将元素放入输出数组i = n - 1while i >= 0:index = arr[i] // expoutput[count[index % 10] - 1] = arr[i]count[index % 10] -= 1i -= 1# 将输出数组的内容复制到原始数组中for i in range(n):arr[i] = output[i]def radix_sort(arr):max_val = max(arr)exp = 1while max_val // exp > 0:counting_sort(arr, exp)exp *= 10# 示例用法
arr = [170, 45, 75, 90, 802, 24, 2, 66]
radix_sort(arr)
print("基数排序后的数组:", arr)
- 基数排序是一种非比较排序算法,它按照每个位数进行排序,从最低位到最高位,依次排列。
- 首先使用计数排序对每个位数进行排序,然后再次对下一个位数进行排序,依次进行直到最高位。
- 这个算法的时间复杂度为 O(nk),其中 k 是数字的最大位数。
9 希尔排序(Shell Sort)
希尔排序(Shell Sort)是一种插入排序的改进版本,也被称为缩小增量排序。希尔排序通过将数组分成若干个子序列来排序数据,然后逐渐缩小子序列的间隔,最终得到一个完全排序的数组。希尔排序的主要思想是提前交换较远的元素,以加快排序过程。
算法原理:
选择一个增量序列(间隔序列),通常选择的增量是数组长度的一半,然后逐渐减小增量。
对于每个增量,将数组分成若干个子序列,每个子序列使用插入排序进行排序。
重复步骤2,逐渐减小增量,直到增量为1。
当增量为1时,整个数组成为一个序列,使用插入排序对其进行排序。
def shell_sort(arr):n = len(arr)gap = n // 2 # 初始增量取数组长度的一半while gap > 0:for i in range(gap, n):temp = arr[i]j = i# 使用插入排序对子序列进行排序while j >= gap and arr[j - gap] > temp:arr[j] = arr[j - gap]j -= gaparr[j] = tempgap //= 2 # 缩小增量# 示例用法
arr = [64, 34, 25, 12, 22, 11, 90]
shell_sort(arr)
print("希尔排序后的数组:", arr)
希尔排序的关键在于选择合适的增量序列。常见的增量序列有希尔增量、Hibbard增量、Knuth增量等,不同的增量序列会影响排序的性能。
希尔排序的时间复杂度取决于增量序列的选择,平均时间复杂度通常在 O(n^1.25) 到 O(n^2) 之间,比插入排序要快。
希尔排序是一种不稳定排序算法,适用于中等大小的数据集。虽然不如快速排序和归并排序快,但在某些情况下比插入排序更快。希尔排序通常用于嵌入式系统等资源有限的环境。
10 桶排序(Bucket Sort)
桶排序(Bucket Sort)是一种分布式排序算法,它将元素分散到一组桶中,然后对每个桶中的元素进行排序,最后将所有桶中的元素按顺序合并成一个有序序列。桶排序适用于元素均匀分布在一个范围内的情况,特别适用于浮点数排序。
算法原理:
确定桶的数量和范围,通常根据输入数据的分布来选择桶的数量。如果元素均匀分布在一个范围内,那么可以选择桶的数量等于元素的数量。
将每个元素分配到相应的桶中。元素的分配可以采用不同的方法,例如线性划分或哈希函数。
对每个桶中的元素进行排序,可以使用任何排序算法,通常选择插入排序。
合并所有桶中的元素,按照桶的顺序得到最终的有序序列。
def bucket_sort(arr):# 确定桶的数量,这里选择与输入元素数量相同n = len(arr)if n <= 1:return arr# 初始化桶max_val = max(arr)min_val = min(arr)bucket_range = (max_val - min_val) / n # 每个桶的范围bucket_count = n # 桶的数量等于元素数量buckets = [[] for _ in range(bucket_count)]# 将元素分配到桶中for num in arr:index = int((num - min_val) / bucket_range)buckets[index].append(num)# 对每个桶中的元素进行排序for i in range(bucket_count):buckets[i].sort()# 合并所有桶中的元素sorted_arr = []for bucket in buckets:sorted_arr.extend(bucket)return sorted_arr# 示例用法
arr = [0.897, 0.565, 0.656, 0.1234, 0.665, 0.3434]
arr = bucket_sort(arr)
print("桶排序后的数组:", arr)
桶排序的性能取决于桶的数量和元素的分布。如果元素均匀分布在一个范围内,并且桶的数量足够多,那么桶排序可以非常高效。
桶排序的时间复杂度通常为 O(n + k),其中 n 是元素的数量,k 是桶的数量。
桶排序是一种稳定排序算法,适用于浮点数排序等特定情况。不过,它需要额外的内存空间来存储桶,因此不适用于数据集非常大的情况。
相关文章:

【算法基础】一文掌握十大排序算法,冒泡排序、插入排序、选择排序、归并排序、计数排序、基数排序、希尔排序和堆排序
目录 1 冒泡排序(Bubble Sort) 2 插入排序(Insertion Sort) 3 选择排序(Selection Sort) 4. 快速排序(Quick Sort) 5. 归并排序(Merge Sort) 6 堆排序 …...
:指定数组元素的特定属性进行搜索)
javascript二维数组(3):指定数组元素的特定属性进行搜索
js中对数组, var data [{“name”: “《西游记》”, “author”: “吴承恩”, “cat”: “A级书刊”, “num”: 3},{“name”: “《三国演义》”, “author”: “罗贯中”, “cat”: “A级书刊”, “num”: 8},{“name”: “《红楼梦》”, “author”: “曹雪芹”,…...

使用Qt进行HTTP通信的方法
文章目录 1 HTTP协议简介1.1 HTTP协议的历史和发展1.2 HTTP协议的特点1.3 HTTP的工作过程1.4 请求报文1.5 响应报文 2 使用Qt进行HTTP通信2.1 Qt的HTTP通信类2.2 HTTP通信过程 3 JSON3.1 cJSON库简介3.2 cJSON库的设计思想和数据结构3.3 cJSON库的使用方法 1 HTTP协议简介 1.1…...

第45节——页面中修改redux里的数据
一、什么是action 在 Redux 中,Action 是一个简单的 JavaScript 对象,用于描述对应应用中的某个事件(例如用户操作)所发生的变化。它包含了一个 type 属性,用于表示事件的类型,以及其他一些可选的数据。 …...
)
软考 系统架构设计师系列知识点之软件架构风格(2)
接前一篇文章:软考 系统架构设计师系列知识点之软件架构风格(1) 这个十一注定是一个不能放松、保持“紧”的十一。由于报名了全国计算机技术与软件专业技术资格(水平)考试,11月4号就要考试,因此…...

【C++11】Lambda 表达式:基本使用 和 底层原理
文章目录 Lambda 表达式1. 不考虑捕捉列表1.1 简单使用介绍1.2 简单使用举例 2. 捕捉列表 [ ] 和 mutable 关键字2.1 使用方法传值捕捉传引用捕捉 2.2 捕捉方法一览2.3 使用举例 3. lambda 的底层分析 Lambda 表达式 书写格式: [capture_list](parameters) mutabl…...

【网络安全---ICMP报文分析】Wireshark教程----Wireshark 分析ICMP报文数据试验
一,试验环境搭建 1-1 试验环境示例图 1-2 环境准备 两台kali主机(虚拟机) kali2022 192.168.220.129/24 kali2022 192.168.220.3/27 1-2-1 网关配置: 编辑-------- 虚拟网路编辑器 更改设置进来以后 ,先选择N…...

【Docker】Docker的应用包含Sandbox、PaaS、Open Solution以及IT运维概念的详细讲解
前言 Docker 是一个开源的应用容器引擎,让开发者可以打包他们的应用以及依赖包到一个可移植的容器中,然后发布到任何流行的Linux或Windows操作系统的机器上,也可以实现虚拟化,容器是完全使用沙箱机制,相互之间不会有任何接口。 📕作者简介:热…...

Java Applet基础
Java Applet基础 目录 Java Applet基础 Applet的生命周期 "Hello, World" Applet: Applet 类 Applet的调用 获得applet参数 指定applet参数 应用程序转换成Applet 事件处理 显示图片 播放音频 applet是一种Java程序。它一般运行在支持Java的Web浏览器内。因…...
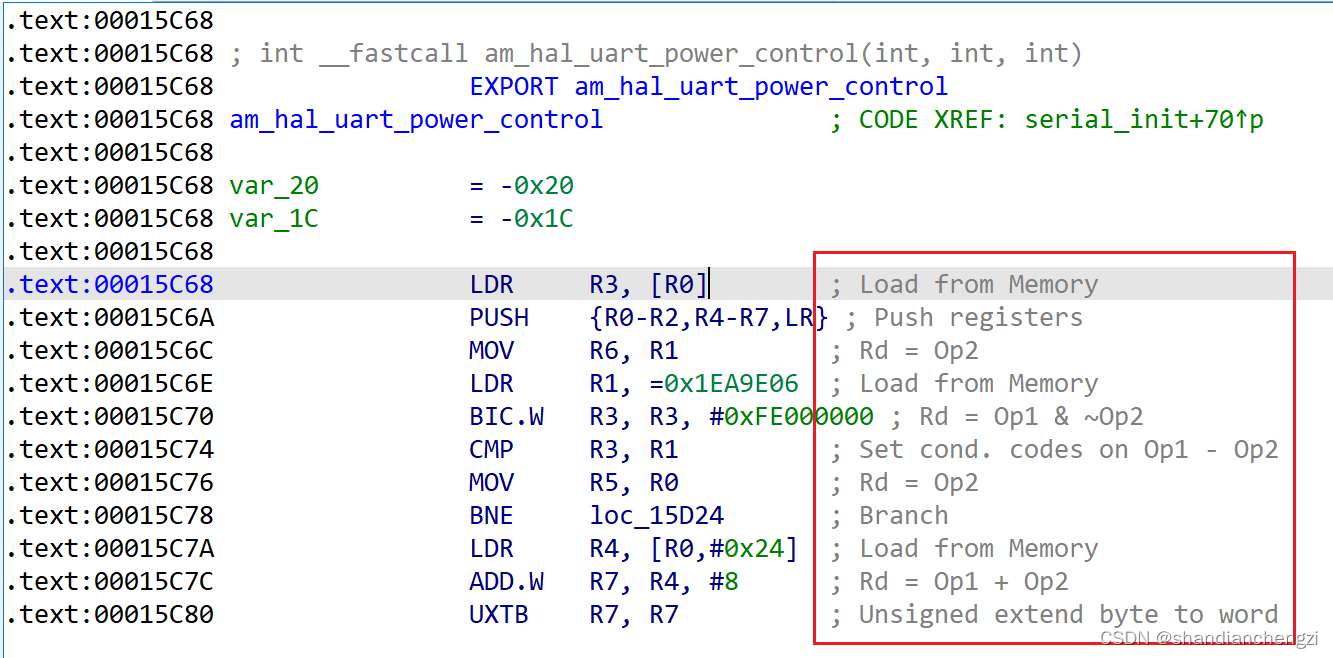
【记录】IDA|IDA怎么查看当前二进制文件自动分析出来的内存分布情况(内存范围和读写性)
IDA版本:7.6 背景:我之前一直是直接看Text View里面的地址的首尾地址来判断内存分布情况的,似乎是有点不准确,然后才想到IDA肯定自带查看内存分布情况的功能,而且很简单。 可以通过View-Toolbars-Segments,…...

LIMS实验室信息管理系统源码 基于计算机的数据处理技术、数据存储技术、网络传输技术、自动化仪器分析技术于一体
LIMS 是一个集现代化管理思想与基于计算机的数据处理技术、数据存储技术、网络传输技术、自动化仪器分析技术于一体,以实验室业务和管理工作为核心,遵循实验室管理国际规范,实现对实验室全方位管理的信息管理系统。 LIMS将样品管理、数据管理…...

有效括号相关
相关题目 20. 有效的括号 921. 使括号有效的最少添加 1541. 平衡括号字符串的最少插入次数 32. 最长有效括号 # 20. 有效的括号 class Solution:def isValid(self, s: str) -> bool:stack []for pare in s:if pare in ([{:stack.append(pare)if not stack or (pare ) and…...

浅谈泛型擦除
文章目录 泛型擦除(1)转换泛型表达式(2)转换泛型方法泛型擦除带来的问题 泛型擦除 在编码阶段使用泛型时加上的类型参数,会被编译器在编译阶段去掉,这个过程叫做泛型擦除。 泛型主要用于编译阶段。在编译后生成的Java字节码文件中不包含泛型中的类型信息…...
nodejs+vue校园跑腿系统elementui
购物车品结算,管理个人中心,订单管理,接单处理,商品维护,用户管理,系统管理等功育食5)要求系统运行可靠、性能稳定、界面友好、使用方便。 第三章 系统分析 10 3.1需求分析 10 3.2可行性分析 10 3.2.1技术…...

Redis Cluster Cron调度
返回目录 说明 clusterCron 每秒执行10次clusterCron 内置了一个iteration计数器。每一次运行clusterCron,iteration都加1。当 iteration % 10 0的时候,就会随机选取一个节点,给它发送PING。而由于clusterCron每秒执行10次,所以…...

Redis Cluster Gossip Protocol: Message
返回目录 消息结构 消息头部消息数据(可选)extension(可选) 消息头部 字段定义 Signature: “RCmb” 这4个字符(Redis Cluster message bus 的简称)totalLen: 消息的总字节数version:当前为…...
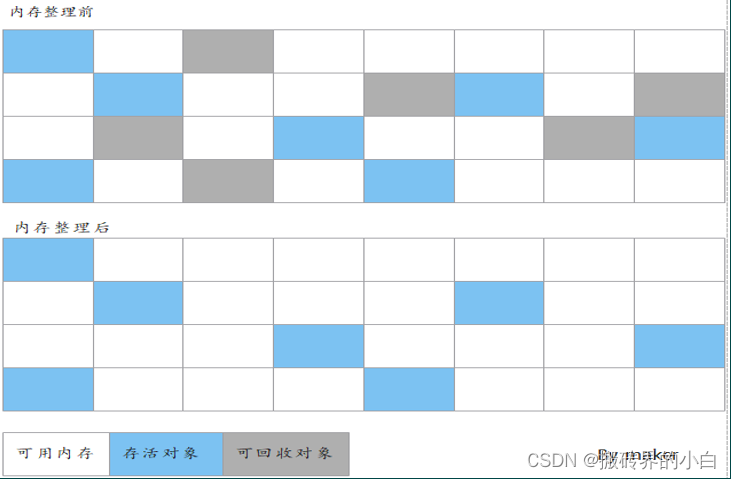
【JVM】第四篇 垃圾收集器ParNewCMS底层三色标记算法详解
导航 一. 垃圾收集算法详解1. 分代收集算法2. 标记-复制算法3. 标记-清除算法4. 标记-整理算法二. 垃圾收集器详解1. Serial收集器2. Parallel Scavenge收集器3. ParNew收集器4. CMS收集器三. 垃圾收集底层三色标记算法实现原理1. 垃圾收集底层使用三色标记算法的原因?2. 垃圾…...
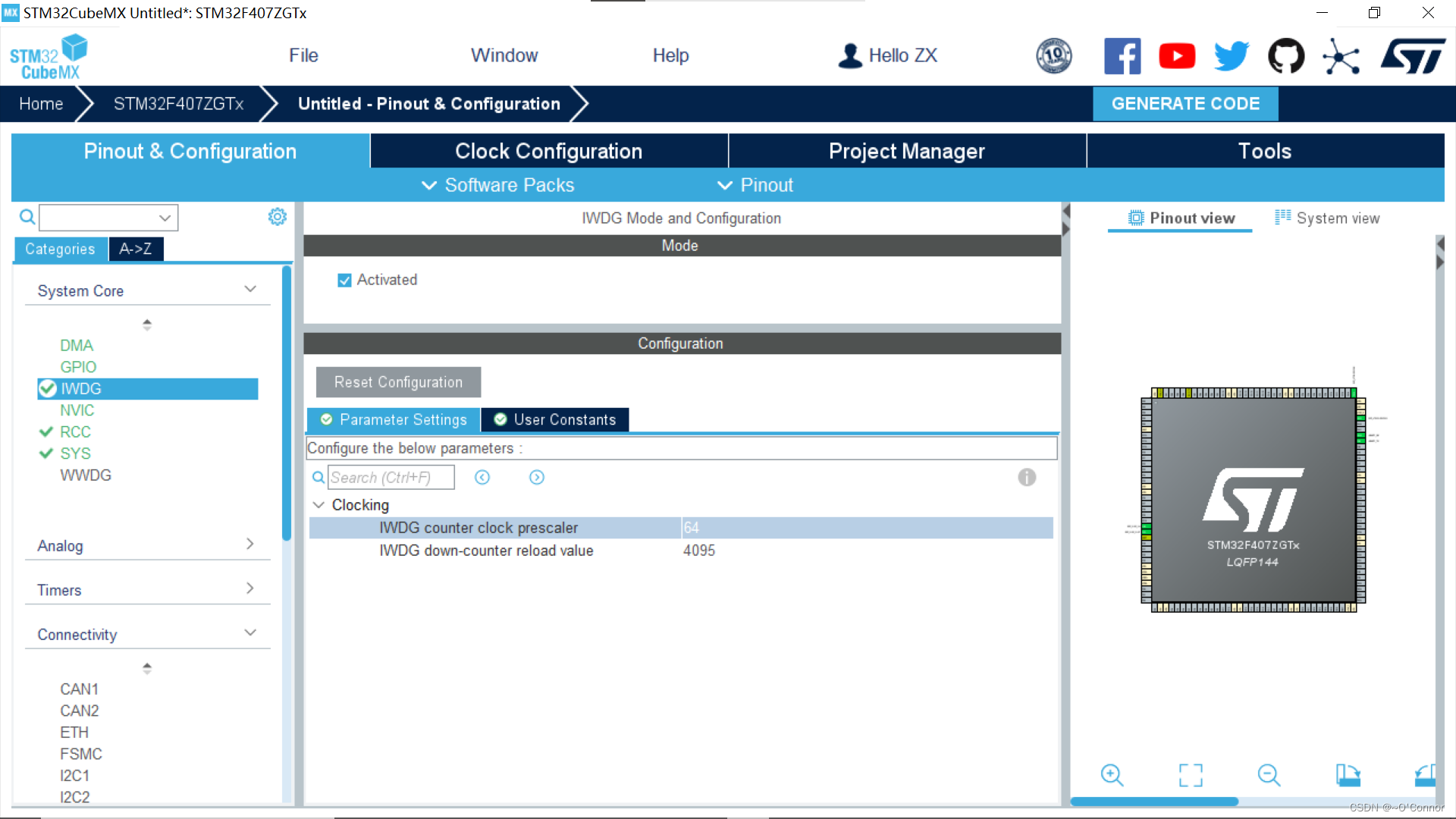
STM32复习笔记(四):独立看门狗IWDG
目录 (一)简介 (二)CUBEMX工程配置 (三)相关函数 总结: (一)简介 独立看门狗本质是一种定时器,其作用是监视系统的运行,当系统发生错误&…...

SpringBoot中常用注解的含义
一、方法参数注解 1. PathVariable 通过RequestMapping注解中的 { } 占位符来标识URL中的变量部分 在控制器中的处理方法的形参中使用PathVariable注解去获取RequestMapping中 { } 中传进来的值,并绑定到处理方法定一的形参上。 //请求路径:http://3333…...

学位论文的写作方法,较好的参考文章
摘要 结合2个文章: [1]程鑫. 网联环境下交通状态预测与诱导技术研究[D]. 长安大学, 2017. [2]吴昊. 关中平原水资源变化特征与干旱脆弱性研究[D]. 长安大学, 2018. 主要研究内容及技术路线 各章小结和引言的写作 [1]程鑫. 网联环境下交通状态预测与诱导技术…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

基于Java+MySQL实现(GUI)客户管理系统
客户资料管理系统的设计与实现 第一章 需求分析 1.1 需求总体介绍 本项目为了方便维护客户信息为了方便维护客户信息,对客户进行统一管理,可以把所有客户信息录入系统,进行维护和统计功能。可通过文件的方式保存相关录入数据,对…...

STM32HAL库USART源代码解析及应用
STM32HAL库USART源代码解析 前言STM32CubeIDE配置串口USART和UART的选择使用模式参数设置GPIO配置DMA配置中断配置硬件流控制使能生成代码解析和使用方法串口初始化__UART_HandleTypeDef结构体浅析HAL库代码实际使用方法使用轮询方式发送使用轮询方式接收使用中断方式发送使用中…...

【Linux系统】Linux环境变量:系统配置的隐形指挥官
。# Linux系列 文章目录 前言一、环境变量的概念二、常见的环境变量三、环境变量特点及其相关指令3.1 环境变量的全局性3.2、环境变量的生命周期 四、环境变量的组织方式五、C语言对环境变量的操作5.1 设置环境变量:setenv5.2 删除环境变量:unsetenv5.3 遍历所有环境…...

结构化文件管理实战:实现目录自动创建与归类
手动操作容易因疲劳或疏忽导致命名错误、路径混乱等问题,进而引发后续程序异常。使用工具进行标准化操作,能有效降低出错概率。 需要快速整理大量文件的技术用户而言,这款工具提供了一种轻便高效的解决方案。程序体积仅有 156KB,…...
