想要精通算法和SQL的成长之路 - 二叉树的判断问题(子树判断 | 对称性 | 一致性判断)
想要精通算法和SQL的成长之路 - 二叉树的判断问题
- 前言
- 一. 相同的树
- 二. 对称二叉树
- 三. 判断子树
前言
想要精通算法和SQL的成长之路 - 系列导航
一. 相同的树
原题链接
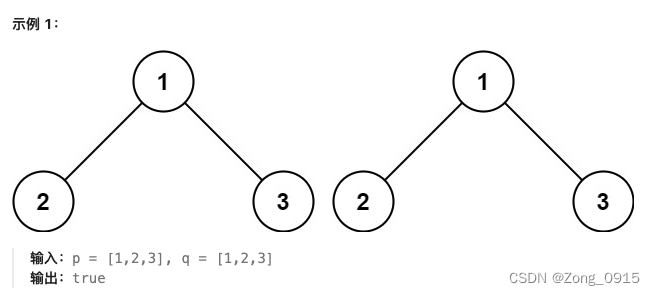
这题目典型的递归题:
- 如果两个节点都是
null,我们返回true。 - 如果两个节点一个
null,一个非空,返回false。 - 最后满足条件:当前两个节点值相等,并且两个节点的左子树相等,右子树也相等。
代码如下:
public boolean isSameTree(TreeNode p, TreeNode q) {if (p == null && q == null) {return true;}if (p == null || q == null) {return false;}return p.val == q.val && isSameTree(p.left, q.left) && isSameTree(p.right, q.right);
}
二. 对称二叉树
原题链接
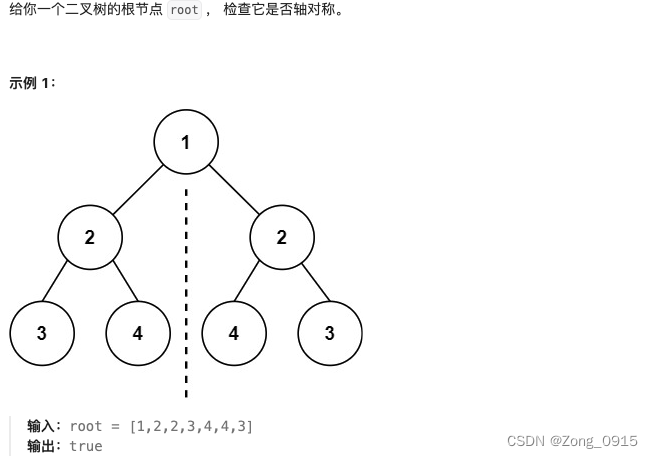
这个题目,我们依旧使用递归算法。我们可以在第一题的基础上,做一个改变。
一致性代码:
return p.val == q.val && isSameTree(p.left, q.left) && isSameTree(p.right, q.right);
对称代码:
return p.val == q.val && isSameTree(p.left, q.right) && isSameTree(p.right, q.left);
最终完整代码如下:
public boolean isSymmetric(TreeNode root) {return helper(root.left, root.right);
}public boolean helper(TreeNode p, TreeNode q) {if (p == null && q == null) {return true;}if (p == null || q == null) {return false;}return p.val == q.val && helper(p.left, q.right) && helper(p.right, q.left);
}
三. 判断子树
原题链接
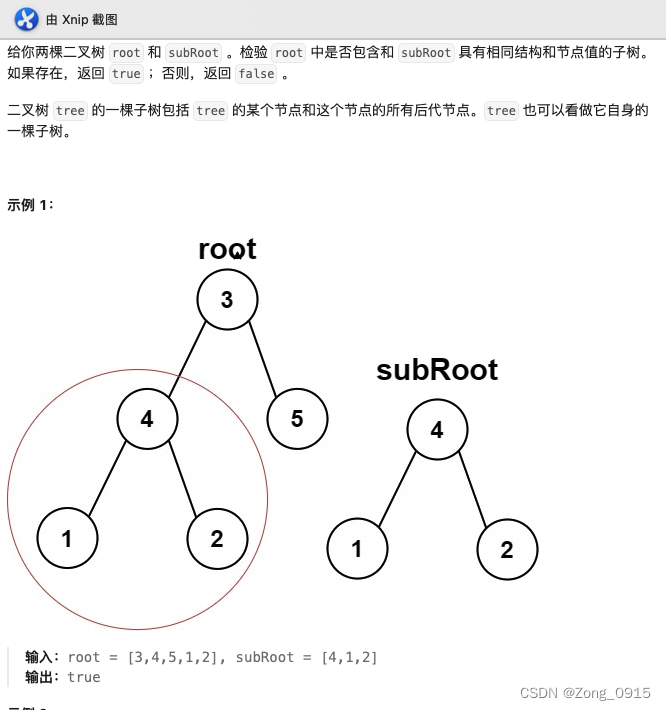
此题依旧是第一题的一个进阶版,判断B是否是A的子树可以等同于:
A和B是否相同?A.left和B是否相同?A.right和B是否相同?- 以此类推…
那么在第一题的基础上,我们有了函数去判断两棵树是否相等,我们只需要完成上面的判断即可:
public boolean isSubtree(TreeNode root, TreeNode subRoot) {// 特判:root肯定不能为nullif (root == null) {return false;}// 特判:subRoot子树允许为nullif (subRoot == null) {return true;}return isSubtree(root.left, subRoot) || isSubtree(root.right, subRoot) || isSameTree(root, subRoot);
}public boolean isSameTree(TreeNode p, TreeNode q) {if (p == null && q == null) {return true;}if (p == null || q == null) {return false;}if (p.val != q.val) {return false;}return p.val == q.val && isSameTree(p.left, q.left) && isSameTree(p.right, q.right);
}
相关文章:

想要精通算法和SQL的成长之路 - 二叉树的判断问题(子树判断 | 对称性 | 一致性判断)
想要精通算法和SQL的成长之路 - 二叉树的判断问题 前言一. 相同的树二. 对称二叉树三. 判断子树 前言 想要精通算法和SQL的成长之路 - 系列导航 一. 相同的树 原题链接 这题目典型的递归题: 如果两个节点都是null,我们返回true。如果两个节点一个nul…...
如何做机器视觉项目)
(零)如何做机器视觉项目
文章目录 1 项目的前期准备1.1 从5个方面初步分析客户需求1.2 方案评估与验证1.3 签订合同 2 项目规划2.1 定义客户端的详细需求2.2 制定项目管理计划2.3 方案评审 3 详细设计3.1 硬件设备的选择与环境搭建3.2 软件开发平台与开发工具的选择3.3 机器视觉系统的整体框架与开发流…...

【Leetcode】滑动窗口合集
这里写目录标题 209.长度最小的子数组题目思路代码 3. 无重复字符的最长子串(medium)题目思路 11. 最大连续 1 的个数 III题目思路 1658. 将 x 减到 0 的最⼩操作数题目思路代码 904. 水果成篮题目思路代码 438.找到字符串中所有字母的异位词题目思路代码…...

【C++】STL详解(九)—— set、map、multiset、multimap的介绍及使用
📝个人主页:Sherry的成长之路 🏠学习社区:Sherry的成长之路(个人社区) 📖专栏链接:C学习 🎯长路漫漫浩浩,万事皆有期待 上一篇博客:【C】STL…...
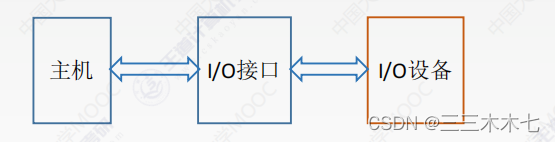
计组—— I/O系统
📕:参考王道课件 目录 一、I/O系统的基本概念 1.什么是“I/O”? 编辑2.主机如何和I/O设备进行交互? 3.I/O控制方式 (1)程序查询方式 (2)程序中断方式 (3&#x…...
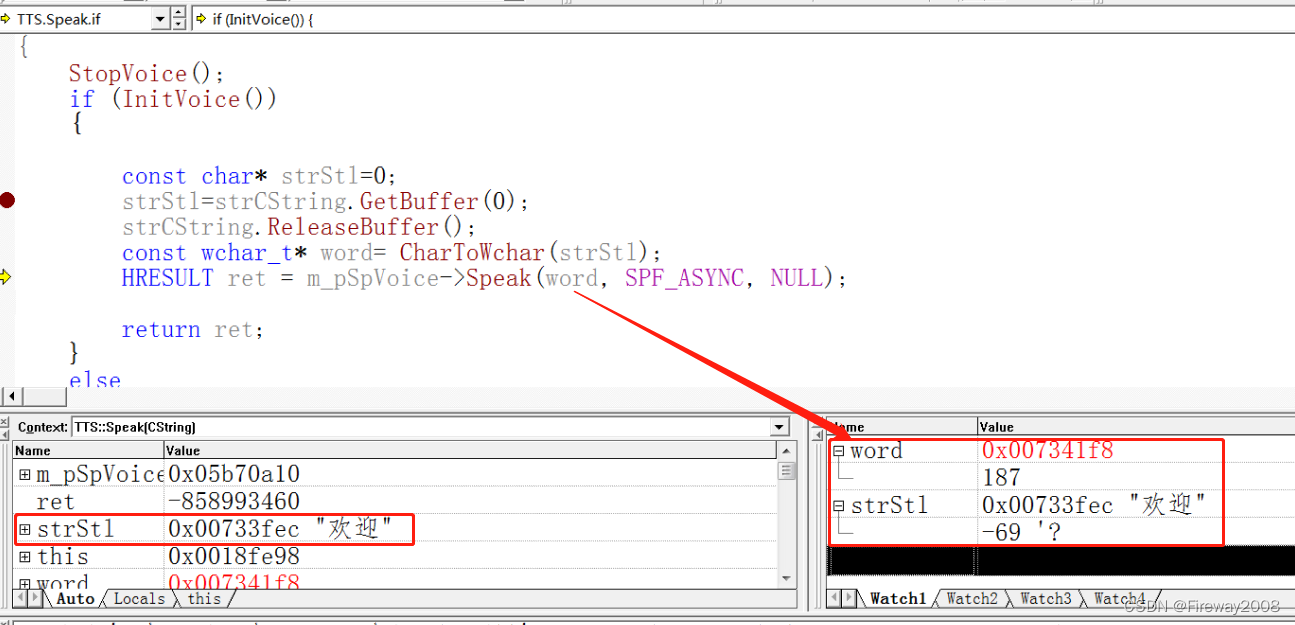
基于vc6+sdk51开发简易文字识别转语音的程序
系统:window7 软件:vc6.0 目的:简易文字转语音真人发声 利用2023国庆小长假,研究如何将文言转语音,之前在网上查询相关知识,大致了解微信语音转换,翻译官之类软件的原理,但要加入神…...
)
DevOps:自动化部署和持续集成/持续交付(CI/CD)
DevOps:自动化部署和持续集成/持续交付(CI/CD) 在现代软件开发领域,DevOps(Development和Operations的组合)已经成为一个不可或缺的概念。它代表了一种将软件开发和运维(Operations)…...

专业图标制作软件 Image2icon 最新中文 for mac
Image2Icon是一款用于Mac操作系统的图标转换工具。它允许用户将常见的图像文件(如PNG、JPEG、GIF等)转换为图标文件(.ico格式),以便在Mac上用作应用程序、文件夹或驱动器的自定义图标。 以下是Image2Icon的一些主要功…...

数据结构:顺序表
SeqList.h #pragma once #include<stdio.h> #include<assert.h> #include<stdlib.h>typedef int SLDataType; //#define NULL 0typedef struct SeqList {SLDataType* a;int size;//顺序表中存储的有效元素的个数int capacity;//空间的大小 }SL;void SLInit(…...
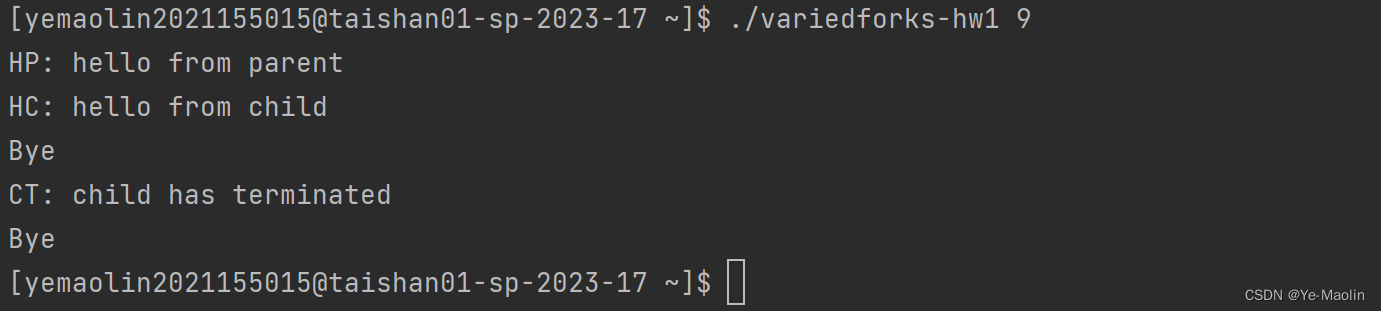
僵尸进程的产生与处理
僵尸进程(Zombie Process)是指在操作系统中已经完成了执行,但其父进程尚未调用wait()或waitpid()来获取其终止状态的子进程。当一个进程结束时,操作系统会保留该进程的一些基本信息,包括进程ID(PID…...

TouchEffects - Android View点击特效
官网 GitHub - likaiyuan559/TouchEffects: Android View点击特效TouchEffects,几行代码为所有控件添加点击效果 项目简介 Android View点击特效TouchEffects,几行代码为所有控件添加点击效果 TouchEffects能够帮助你更快速方便的增加点击时候的效果,TouchEffect…...

从ContinuousEventTimeTrigger/ContinuousProcessingTimeTrigger代码看如何实现一个自定义的触发器
背景 当我们想要实现提前触发计算的触发器时,我们可以使用ContinuousEventTimeTrigger/ContinuousProcessingTimeTrigger作为触发器达到比如几分钟触发一次计算并发送计算结果的类,我们本文就从代码角度解析下实现自定义触发器的一些注意事项 Continuo…...
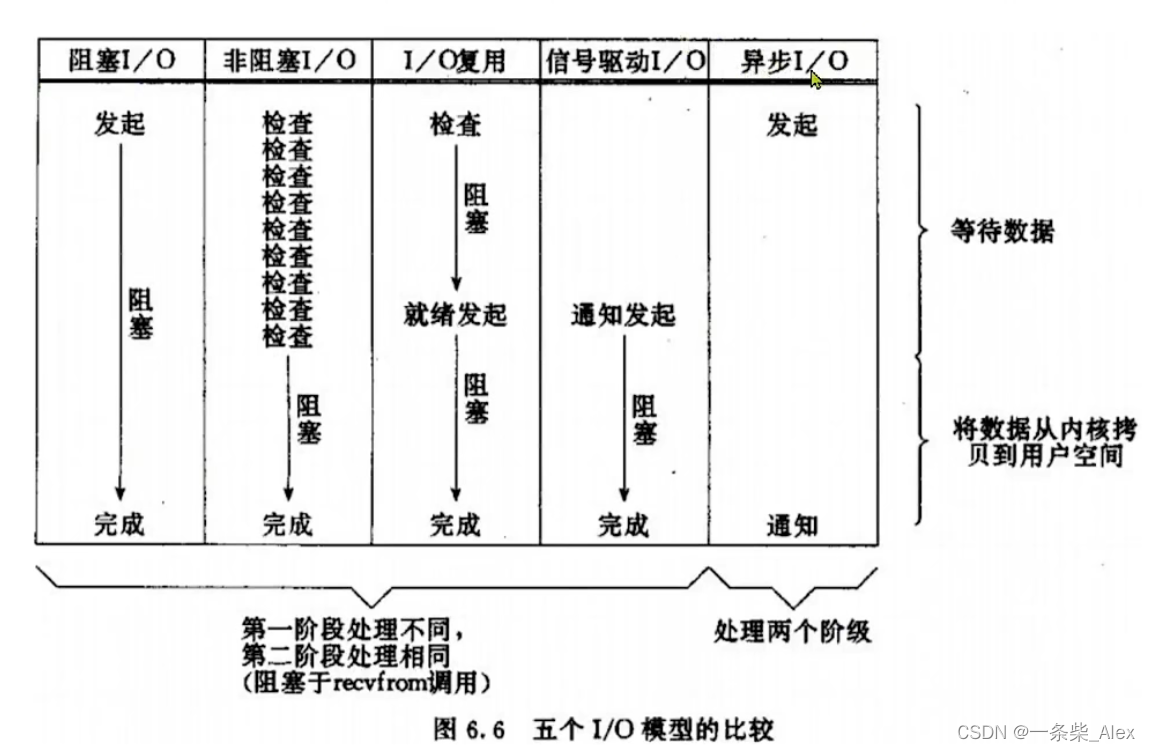
Linux 5种网络模型
[参考]:《黑马程序员Redis》https://www.bilibili.com/video/BV1cr4y1671t/?p166&share_sourcecopy_web&vd_source9e65300ccca322aeb367bb1eb677b0fc [参考]:《操作系统》 [参考]:《UNIX网络编程》 为了避免用户应用导致冲突甚至内…...
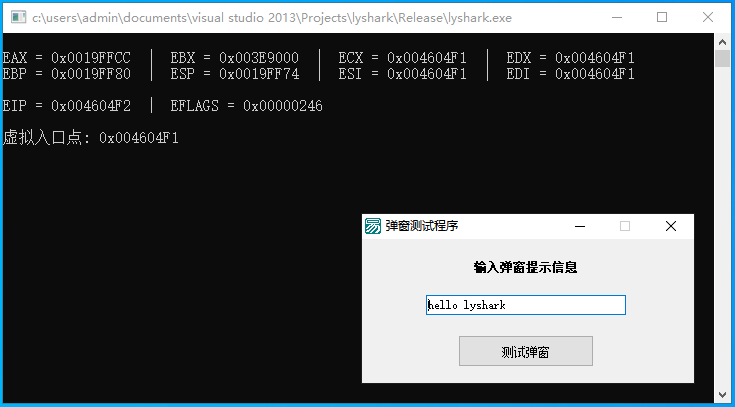
10.1 调试事件读取寄存器
当读者需要获取到特定进程内的寄存器信息时,则需要在上述代码中进行完善,首先需要编写CREATE_PROCESS_DEBUG_EVENT事件,程序被首次加载进入内存时会被触发此事件,在该事件内首先我们通过lpStartAddress属性获取到当前程序的入口地…...

Linux系统常用指令篇---(一)
Linux系统常用指令篇—(一) 1.cd指令 Linux系统中,磁盘上的文件和目录被组成一棵目录树,每个节点都是目录或文件。 语法:cd 目录名 功能:改变工作目录。将当前工作目录改变到指定的目录下。 (简单理解为进入指定目录下) 举例: cd .. : 返…...

【初识Linux】:常见指令(1)
朋友们、伙计们,我们又见面了,本期来给大家解读一下有关Linux的基础知识点,如果看完之后对你有一定的启发,那么请留下你的三连,祝大家心想事成! C 语 言 专 栏:C语言:从入门到精通 数…...
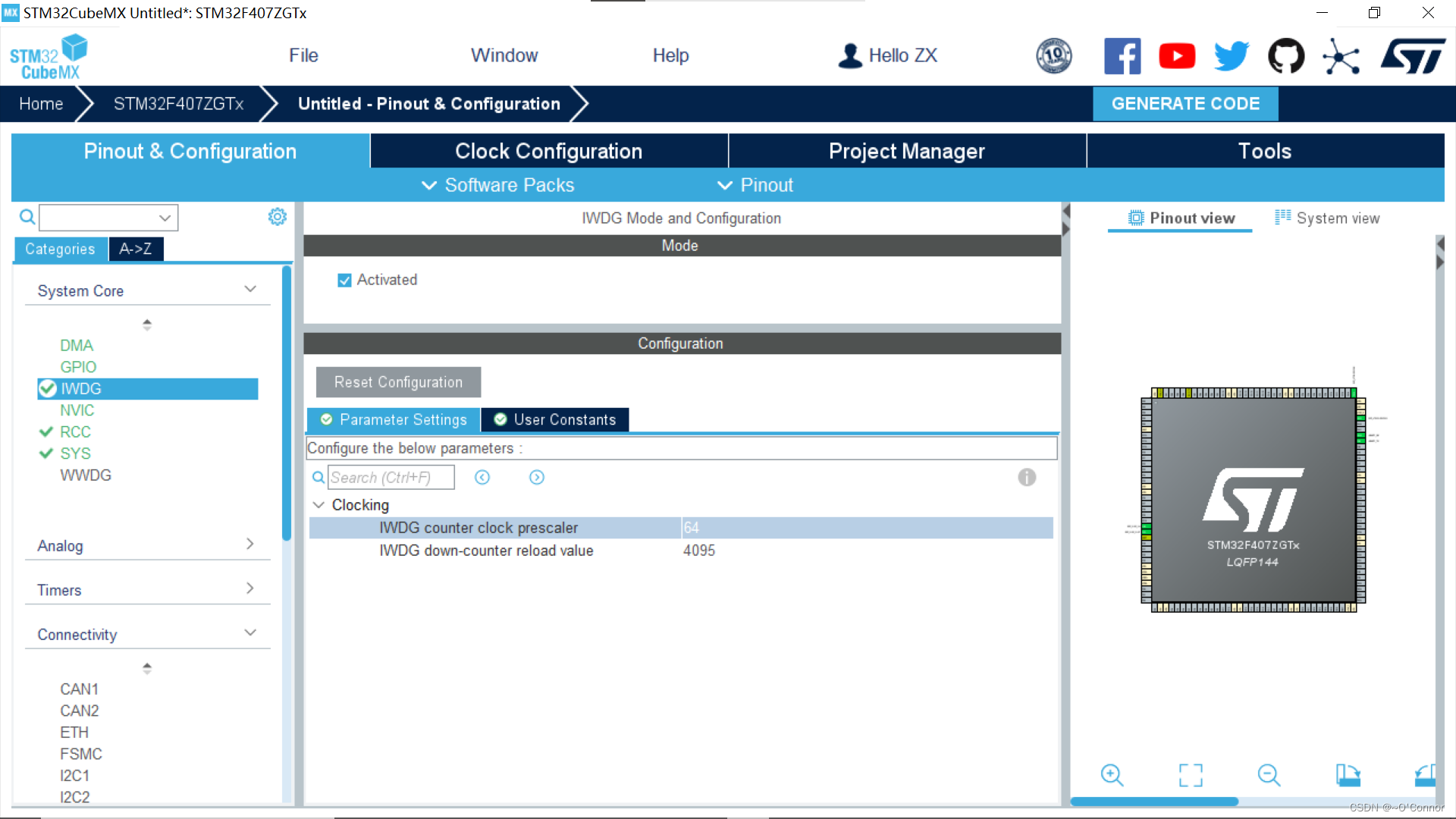
STM32复习笔记(四):看门狗
目录 (一)简介 (二)IWDG IWDG的CUBEMX工程配置 IWDG相关函数(非常少,所以直接贴上来): (三)WWDG (一)简介 看门狗分为独立看门…...

【C++进阶(七)】仿函数深度剖析模板进阶讲解
💓博主CSDN主页:杭电码农-NEO💓 ⏩专栏分类:C从入门到精通⏪ 🚚代码仓库:NEO的学习日记🚚 🌹关注我🫵带你学习C 🔝🔝 模板进阶 1. 前言2. 仿函数的概念3. 仿函数的实…...
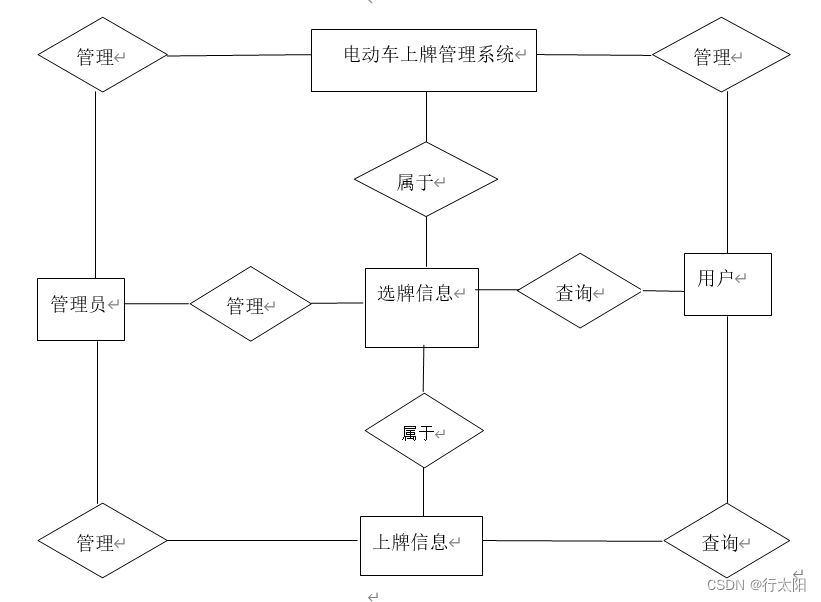
基于SSM的电动车上牌管理系统(有报告)。Javaee项目。
演示视频: 基于SSM的电动车上牌管理系统(有报告)。Javaee项目。 项目介绍: 采用M(model)V(view)C(controller)三层体系结构,通过Spring SpringM…...
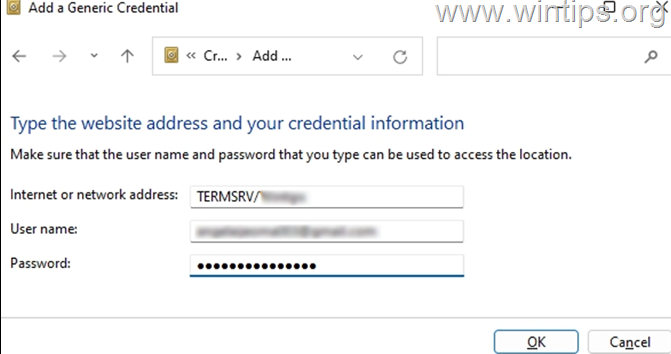
mstsc无法保存RDP凭据, 100%生效
问题 即使如下两项都打勾,其还是无法保存凭据,特别是连接Ubuntu (freerdp server): 解决方法 网上多种复杂方法,不生效,其思路是修改后台配置,以使mstsc跟平常一样自动记住凭据。最后,如下的…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

C#中的CLR属性、依赖属性与附加属性
CLR属性的主要特征 封装性: 隐藏字段的实现细节 提供对字段的受控访问 访问控制: 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性: 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑: 可以…...

Proxmox Mail Gateway安装指南:从零开始配置高效邮件过滤系统
💝💝💝欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:「storms…...

永磁同步电机无速度算法--基于卡尔曼滤波器的滑模观测器
一、原理介绍 传统滑模观测器采用如下结构: 传统SMO中LPF会带来相位延迟和幅值衰减,并且需要额外的相位补偿。 采用扩展卡尔曼滤波器代替常用低通滤波器(LPF),可以去除高次谐波,并且不用相位补偿就可以获得一个误差较小的转子位…...

redis和redission的区别
Redis 和 Redisson 是两个密切相关但又本质不同的技术,它们扮演着完全不同的角色: Redis: 内存数据库/数据结构存储 本质: 它是一个开源的、高性能的、基于内存的 键值存储数据库。它也可以将数据持久化到磁盘。 核心功能: 提供丰…...
