(枚举 + 树上倍增)Codeforces Round 900 (Div. 3) G
Problem - G - Codeforces
题意:

思路:
首先,目标值和结点权值是直接联系的,最值不可能直接贪心,一定是考虑去枚举一些东西,依靠这种枚举可以遍历所有的有效情况,思考的方向一定是枚举
如果去直接在链上枚举的话, 复杂度是O(nq),肯定不行
注意到一条路径上的前缀或值不会超过 logV个,因此考虑枚举前缀或值

关于每次跳使前缀或值变化的最深的点,我是这样理解的
如果考虑在链上枚举,如果前缀或值不变,那么这样的枚举是无效的,我们直接考虑跳着枚举,只枚举所有有效情况
关于怎么跳其实可以参考树上倍增往上跳的跳法,记录一个数组指向下一个结点,在dfs上维护即可,有点像在树链上DP
Code:
#include <bits/stdc++.h>#define int long longconstexpr int N = 2e5 + 10;std::vector<int> adj[N];int n;
int a[N];
int dep[N];
int f[N][33], s[N][33], lst[N][33];void dfs(int u, int fa) {dep[u] = dep[fa] + 1;f[u][0] = fa;for (int j = 1; j <= 30; j ++) f[u][j] = f[f[u][j - 1]][j - 1];int val = a[u];for (int j = 30; j >= 0; j --) {if (!((val >> j) & 1)) {lst[u][j] = lst[fa][j];s[u][j] = s[fa][j];}else {lst[u][j] = u;s[u][j] = s[fa][j] + 1;}}for (auto v : adj[u]) {if (v == fa) continue;dfs(v, u);}
}
int lca(int u, int v) {if (dep[u] < dep[v]) std::swap(u, v);for (int j = 30; j >= 0; j --) {if (dep[f[u][j]] >= dep[v]) {u = f[u][j];}}if (u == v) return u;for (int j = 30; j >= 0; j --) {if (f[u][j] != f[v][j]) {u = f[u][j];v = f[v][j];}}return f[u][0];
}
int calc(int x, int y, int lca) {int res = 0;for (int j = 0; j <= 30; j ++) {if (s[x][j] + s[y][j] - s[lca][j] - s[f[lca][0]][j]) res ++;}return res;
}
void solve() {std::cin >> n;for (int i = 1; i <= n; i ++) {adj[i].clear();dep[i] = 0;for (int j = 30; j >= 0; j --) {f[i][j] = s[i][j] = lst[i][j] = 0;}}for (int i = 1; i <= n; i ++) std::cin >> a[i];for (int i = 1; i <= n - 1; i ++) {int u, v;std::cin >> u >> v;adj[u].push_back(v);adj[v].push_back(u);}dfs(1, 0);int q;int ans = 0;std::cin >> q;while(q --) {int x, y;std::cin >> x >> y;int cur = x, val = a[x];ans = 0;while(1) {int nxt = 0, mx = 0;ans = std::max(ans, calc(x, cur, lca(x, cur)) + calc(cur, y, lca(cur, y)));for (int j = 30; j >= 0; j --) {if (!((val >> j) & 1)) {if (dep[lst[cur][j]] >= dep[lca(x, y)]) {if (dep[lst[cur][j]] > mx) {mx = dep[lst[cur][j]];nxt = lst[cur][j];}}}}if (!mx) break;val |= a[nxt];cur = nxt;}cur = y, val = a[y];while(1) {int nxt = 0, mx = 0;ans = std::max(ans, calc(x, cur, lca(x, cur)) + calc(cur, y, lca(cur, y)));for (int j = 30; j >= 0; j --) {if (!((val >> j) & 1)) {if (dep[lst[cur][j]] >= dep[lca(x, y)]) {if (dep[lst[cur][j]] > mx) {mx = dep[lst[cur][j]];nxt = lst[cur][j];}}}}if (!mx) break;val |= a[nxt];cur = nxt;}std::cout << ans << " ";}std::cout << "\n";
}
signed main() {std::ios::sync_with_stdio(false);std::cin.tie(nullptr);int t = 1;std::cin >> t;while(t --) {solve();}return 0;
}相关文章:

(枚举 + 树上倍增)Codeforces Round 900 (Div. 3) G
Problem - G - Codeforces 题意: 思路: 首先,目标值和结点权值是直接联系的,最值不可能直接贪心,一定是考虑去枚举一些东西,依靠这种枚举可以遍历所有的有效情况,思考的方向一定是枚举 如果去…...
websocket逆向【python实现websocket拦截】
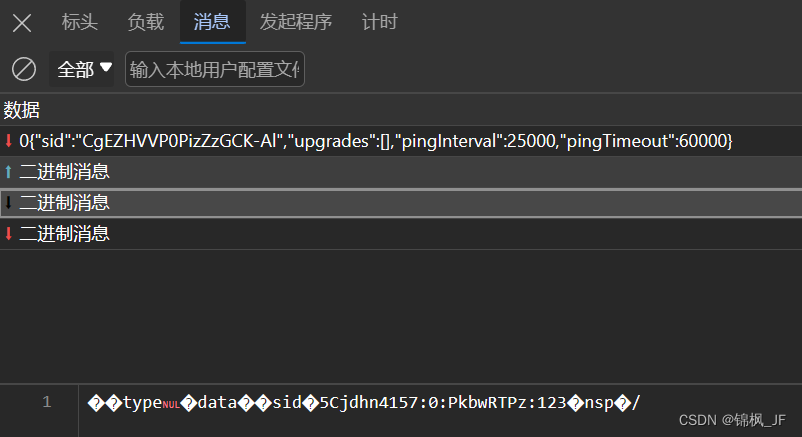
python实现websocket拦截 前言一、拦截的优缺点优点:缺点:二、实现方法1.环境配置2.代码三、总结前言 开发者工具F12,筛选ws后,websocket的消息是这样显示的,如何获取这里面的消息呢? 以下是本篇文章正文内容 一、拦截的优缺点 主要讲解一下websocket拦截的实现,现在…...

软件测试自动化的成本效益分析
随着软件测试技术的发展,人们已经从最初的手工测试转变为手工和自动化技术相结合的测试方法。目前,人们更多的是关心自动化测试框架、自动化测试工具以及脚本研究等技术方面,而在软件自动化测试方案的效益分析方面涉及较少。 软件测试的目的是…...

【Java】状态修饰符 final static
目录 final 修饰我们的成员方法、成员变量、类 示例代码: final 修饰的局部变量 示例代码: static 示例代码: static 访问特点: 示例代码: static关键字的用途 示例代码: static 修饰常量 示例…...

笔试编程ACM模式JS(V8)、JS(Node)框架、输入输出初始化处理、常用方法、技巧
目录 考试注意事项 先审完题意,再动手 在本地编辑器(有提示) 简单题515min 通过率0%,有额外log 常见输入处理 str-> num arr:line.split( ).map(val>Number(val)) 初始化数组 new Array(length).fill(v…...
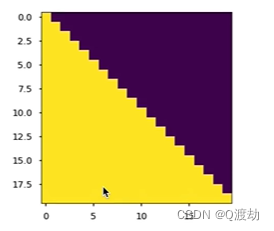
learn掩码张量
目录 1、什么是掩码张量 2、掩码张量的作用 3、代码演示 (1)、定义一个上三角矩阵,k0或者 k默认为 0 (2)、k1 (3)、k-1 4、掩码张量代码实现 (1)、输出效果 &…...
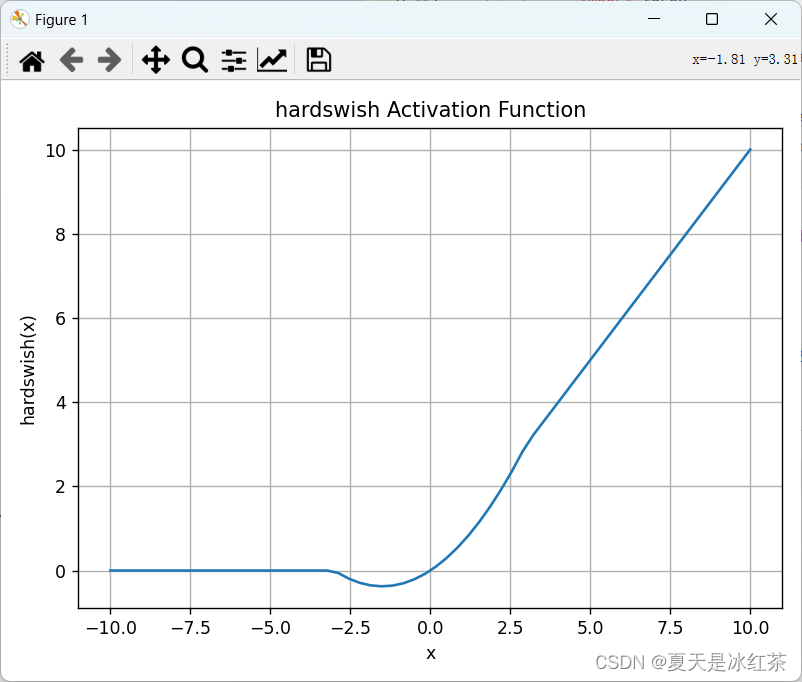
激活函数介绍
介绍 神经网络当中的激活函数用来提升网络的非线性,以增强网络的表征能力。它有这样几个特点:有界,必须为非常数,单调递增且连续可求导。我们常用的有sigmoid或者tanh,但我们都知道这两个都存在一定的缺点,…...
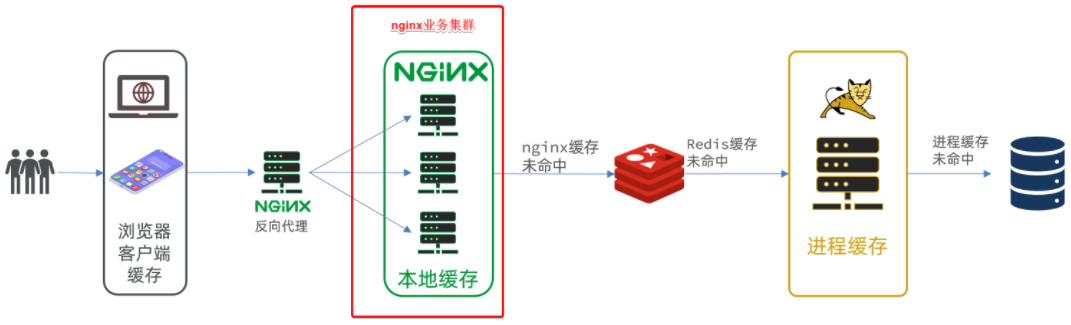
docker方式启动一个java项目-Nginx本地有代码,并配置反向代理
文章目录 案例导入说明1.安装MySQL1.1.准备目录1.2.运行命令1.3.修改配置1.4.重启 2.导入SQL3.导入Demo工程3.1.分页查询商品(仔细看代码,很多新的MP编程技巧)3.2.新增商品3.3.修改商品3.4.修改库存3.5.删除商品3.6.根据id查询商品3.7.根据id…...

前端和后端是Web开发选哪个好?
前端和后端是Web开发中的两个不同的领域,哪一种更适合学习?前景更广呢? 一、引言 Web前端开发就像装饰房间的小瓦匠,勤勤恳恳,仔仔细细,粉饰墙壁,妆点家具。会 HTML,CSS,懂点 JS。…...

HTTP协议,请求响应
、概述 二、HTTP请求协议 三、HTTP响应协议 四、请求数据 1.简单实体参数 RequestMapping("/simpleParam")public String simpleParam(RequestParam(name "name" ,required false ) String username, Integer age){System.out.println (username "…...
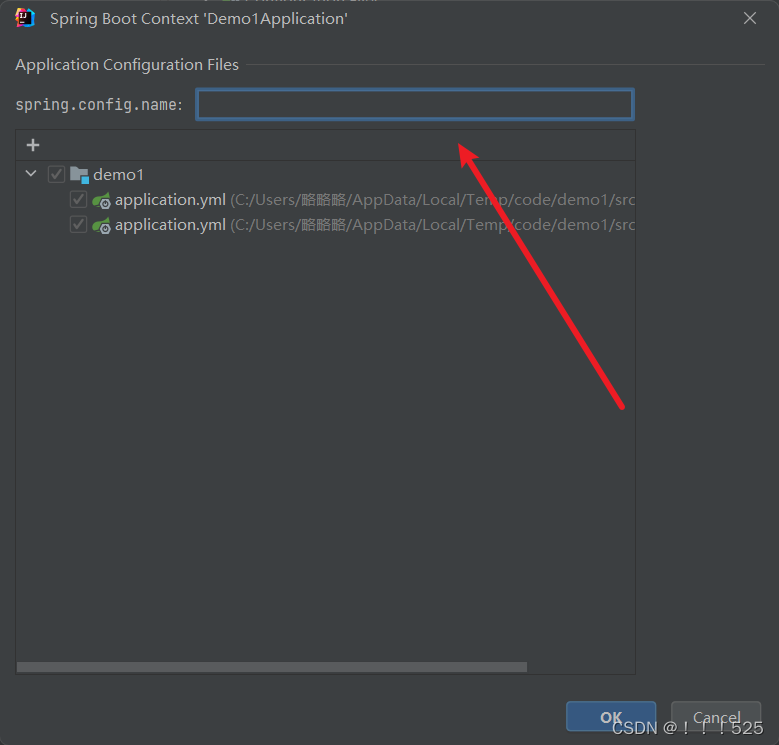
idea配置文件属性提示消息解决方案
在项目文件路径下找到你没有属性提示消息的文件 选中,ok即可 如果遇到ok无法确认的情况: 在下图所示位置填写配置文件名称即可...

EdgeView 4 for Mac:重新定义您的图像查看体验
您是否厌倦了那些功能繁杂、操作复杂的图像查看器?您是否渴望一款简单、快速且高效的工具,以便更轻松地浏览和管理您的图像库?如果答案是肯定的,那么EdgeView 4 for Mac将是您的理想之选! EdgeView 4是一款专为Mac用户…...
的好处有哪些?)
流程自动化(RPA)的好处有哪些?
流程自动化(RPA)是一种通过软件机器人实现业务流程自动化的技术。它可以模拟人类在计算机上执行的操作,从而自动化重复性、繁琐的任务,提高工作效率和准确性。流程自动化(RPA)的好处很多,下面我…...

医学影像系统【简称PACS】源码
PACS(Picture Archiving and Comuniations Systems)即PACS,图像存储与传输系统,是应用于医院中管理医疗设备如CT,MR等产生的医学图像的信息系统。目标是支持在医院内部所有关于图像的活动,集成了医疗设备,图像存储和分…...

大家都在用哪些敏捷开发项目管理软件?
敏捷开发是一种以人为核心、迭代、循序渐进的开发方法。 敏捷开发的特点是高度灵活性和适应性、迭代式开发。 敏捷开发方法强调快速响应变化,因此它具有高度的灵活性和适应性。开发团队可以根据客户需求和市场变化快速调整开发计划和产品功能,以确保产品…...

python机器学习基础教程01-环境搭建
书籍源代码 github上源代码 https://github.com/amueller/introduction_to_ml_with_python 安装anaconda虚拟环境 创建虚拟环境 conda create -p E:\Python\envs\mlstupy35 python3.5 # 激活环境 conda activate E:\Python\envs\mlstupy35 # 创建学习目录 cd G:\Python\ml…...

TinyWebServer学习笔记-Config
为了弄清楚具体的业务逻辑,我们直接从主函数开始看源代码: #include "config.h"int main(int argc, char *argv[]) {//需要修改的数据库信息,登录名,密码,库名string user "root";string passwd "root";string databas…...

数据结构与算法--算法
这里写目录标题 线性表顺序表链表插入删除算法 一级目录二级目录二级目录二级目录 一级目录二级目录二级目录二级目录 一级目录二级目录二级目录二级目录 一级目录二级目录二级目录二级目录 线性表 顺序表 链表 插入删除算法 步骤 1.通过循环到达指定位置的前一个位置 2.新建…...
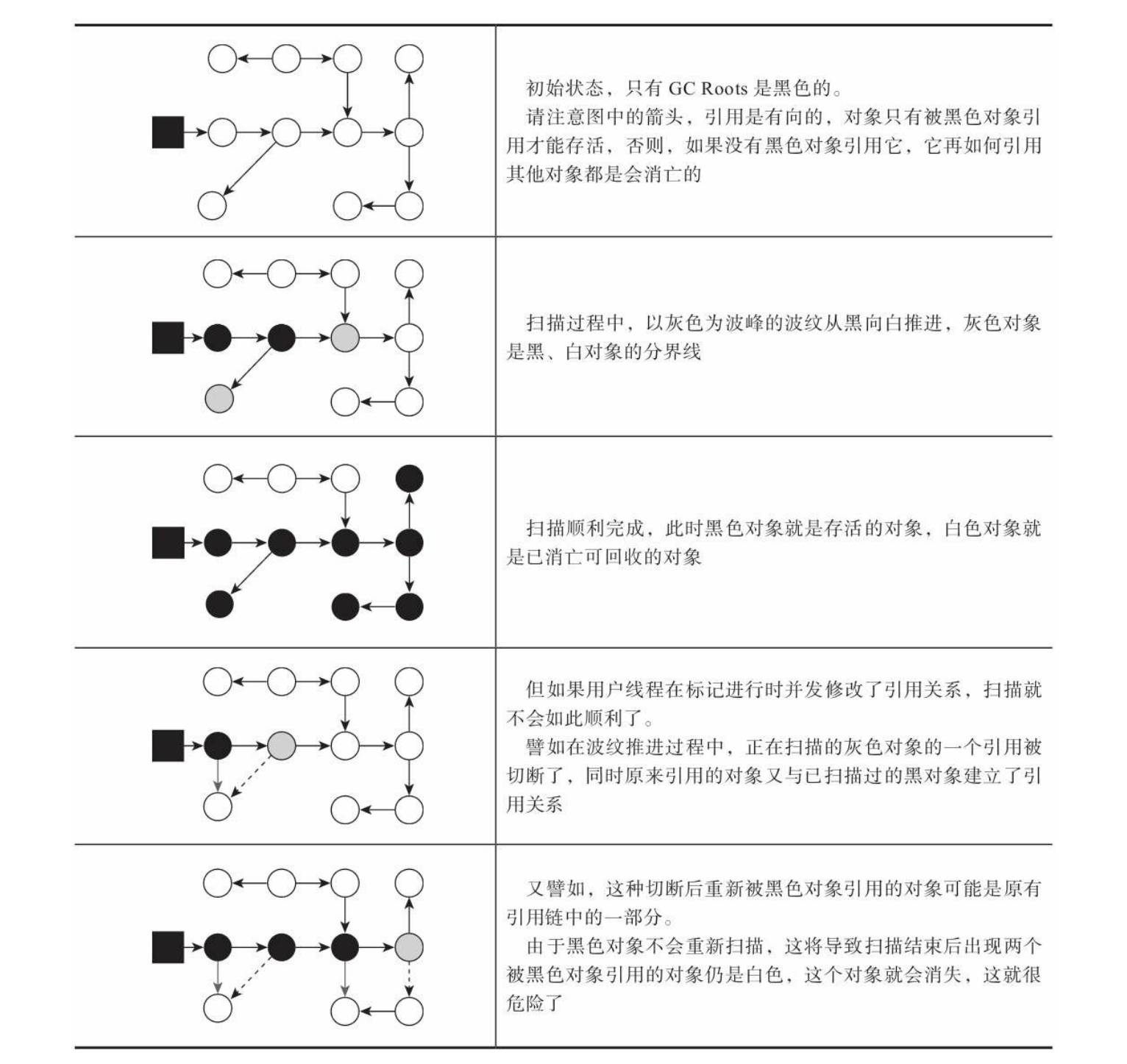
JVM:如何通俗的理解并发的可达性分析
并发的可达性分析 前面在介绍对象是否已死那一节有说到可达性分析算法,它理论上是要求全过程都基于一个能保障一致性的快照(类比 MySQL 的MVCC)中才能够进行分析,也就意味着必须全程冻结用户线程的运行(STW࿰…...

传统机器学习聚类算法——总集篇
工作需要,涉及到一些聚类算法相关的知识。工作中需要综合考虑数据量、算法效果、性能之间的平衡,所以开启新的篇章——机器学习聚类算法篇。 传统机器学习中聚类算法主要分为以下几类: 1. 层次聚类算法 层次聚类算法是一种无监督学习算法&am…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...

【Linux】Linux 系统默认的目录及作用说明
博主介绍:✌全网粉丝23W,CSDN博客专家、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围:SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...
