二叉树题目:路径总和 II
文章目录
- 题目
- 标题和出处
- 难度
- 题目描述
- 要求
- 示例
- 数据范围
- 前言
- 解法一
- 思路和算法
- 代码
- 复杂度分析
- 解法二
- 思路和算法
- 代码
- 复杂度分析
题目
标题和出处
标题:路径总和 II
出处:113. 路径总和 II
难度
4 级
题目描述
要求
给你二叉树的根结点 root \texttt{root} root 和一个表示目标和的整数 targetSum \texttt{targetSum} targetSum,返回所有的满足路径上结点值总和等于目标和 targetSum \texttt{targetSum} targetSum 的从根结点到叶结点的路径。每条路径应该以结点值列表的形式返回,而不是结点的引用。
示例
示例 1:
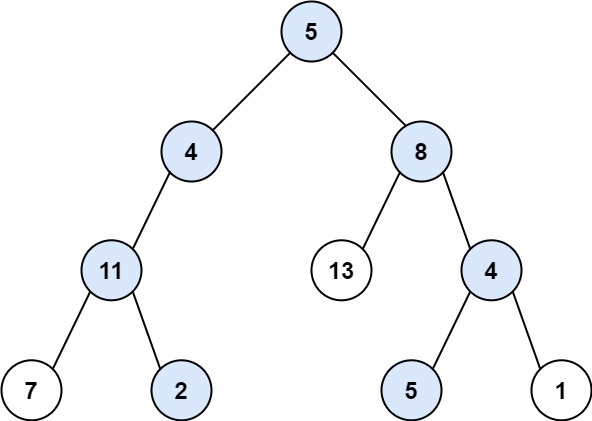
输入: root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22 \texttt{root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22} root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出: [[5,4,11,2],[5,8,4,5]] \texttt{[[5,4,11,2],[5,8,4,5]]} [[5,4,11,2],[5,8,4,5]]
解释:有两条路径的结点值总和等于 targetSum \texttt{targetSum} targetSum:
5 + 4 + 11 + 2 = 22 \texttt{5 + 4 + 11 + 2 = 22} 5 + 4 + 11 + 2 = 22
5 + 8 + 4 + 5 = 22 \texttt{5 + 8 + 4 + 5 = 22} 5 + 8 + 4 + 5 = 22
示例 2:
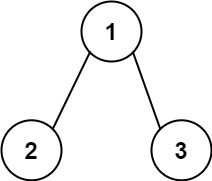
输入: root = [1,2,3], targetSum = 5 \texttt{root = [1,2,3], targetSum = 5} root = [1,2,3], targetSum = 5
输出: [] \texttt{[]} []
示例 3:
输入: root = [1,2], targetSum = 0 \texttt{root = [1,2], targetSum = 0} root = [1,2], targetSum = 0
输出: [] \texttt{[]} []
数据范围
- 树中结点数目在范围 [0, 5000] \texttt{[0, 5000]} [0, 5000] 内
- -1000 ≤ Node.val ≤ 1000 \texttt{-1000} \le \texttt{Node.val} \le \texttt{1000} -1000≤Node.val≤1000
- -1000 ≤ targetSum ≤ 1000 \texttt{-1000} \le \texttt{targetSum} \le \texttt{1000} -1000≤targetSum≤1000
前言
这道题是「路径总和」的进阶,要求返回所有的结点值总和等于目标和的从根结点到叶结点的路径。这道题也可以使用深度优先搜索和广度优先搜索得到答案,在搜索过程中需要维护路径。
解法一
思路和算法
如果二叉树为空,则不存在结点值总和等于目标和的路径。只有当二叉树不为空时,才可能存在结点值总和等于目标和的路径,需要从根结点开始寻找路径。
从根结点开始深度优先搜索,在遍历每一个结点的同时需要维护从根结点到当前结点的路径以及剩余目标和,将原目标和减去当前结点值即可得到剩余目标和。当访问到叶结点时,如果剩余目标和为 0 0 0,则从根结点到当前叶结点的路径即为结点值总和等于目标和的路径,将该路径添加到结果列表中。
由于深度优先搜索过程中维护的路径会随着访问到的结点而变化,因此当找到结点值总和等于目标和的路径时,需要新建一个路径对象添加到结果列表中,避免后续搜索过程中路径变化对结果造成影响。
代码
class Solution {List<List<Integer>> paths = new ArrayList<List<Integer>>();List<Integer> path = new ArrayList<Integer>();public List<List<Integer>> pathSum(TreeNode root, int targetSum) {dfs(root, targetSum);return paths;}public void dfs(TreeNode node, int targetSum) {if (node == null) {return;}path.add(node.val);targetSum -= node.val;if (node.left == null && node.right == null && targetSum == 0) {paths.add(new ArrayList<Integer>(path));}dfs(node.left, targetSum);dfs(node.right, targetSum);path.remove(path.size() - 1);}
}
复杂度分析
-
时间复杂度: O ( n 2 ) O(n^2) O(n2),其中 n n n 是二叉树的结点数。每个结点都被访问一次,最坏情况下每次将路径添加到结果中的时间是 O ( n ) O(n) O(n),因此总时间复杂度是 O ( n 2 ) O(n^2) O(n2)。
-
空间复杂度: O ( n ) O(n) O(n),其中 n n n 是二叉树的结点数。空间复杂度主要是递归调用的栈空间以及深度优先搜索过程中存储路径的空间,取决于二叉树的高度,最坏情况下二叉树的高度是 O ( n ) O(n) O(n)。注意返回值不计入空间复杂度。
解法二
思路和算法
使用广度优先搜索寻找结点值总和等于目标和的路径时,首先找到这些路径对应的叶结点,然后得到从叶结点到根结点的路径,将路径翻转之后即可得到相应的路径。
为了得到从叶结点到根结点的路径,需要使用哈希表存储每个结点的父结点,在广度优先搜索的过程中即可将每个结点和父结点的关系存入哈希表中。
广度优先搜索需要维护两个队列,分别存储结点与对应的结点值总和。广度优先搜索的过程中,如果遇到一个叶结点对应的结点值总和等于目标和,则找到一条结点值总和等于目标和的路径,利用哈希表中存储的父结点信息得到从当前叶结点到根结点的路径,然后将路径翻转,添加到结果中。
代码
class Solution {List<List<Integer>> paths = new ArrayList<List<Integer>>();Map<TreeNode, TreeNode> parents = new HashMap<TreeNode, TreeNode>();public List<List<Integer>> pathSum(TreeNode root, int targetSum) {if (root == null) {return paths;}Queue<TreeNode> nodeQueue = new ArrayDeque<TreeNode>();Queue<Integer> sumQueue = new ArrayDeque<Integer>();nodeQueue.offer(root);sumQueue.offer(root.val);while (!nodeQueue.isEmpty()) {TreeNode node = nodeQueue.poll();int sum = sumQueue.poll();TreeNode left = node.left, right = node.right;if (left == null && right == null && sum == targetSum) {paths.add(getPath(node));}if (left != null) {parents.put(left, node);nodeQueue.offer(left);sumQueue.offer(sum + left.val);}if (right != null) {parents.put(right, node);nodeQueue.offer(right);sumQueue.offer(sum + right.val);}}return paths;}public List<Integer> getPath(TreeNode node) {List<Integer> path = new ArrayList<Integer>();while (node != null) {path.add(node.val);node = parents.get(node);}Collections.reverse(path);return path;}
}
复杂度分析
-
时间复杂度: O ( n 2 ) O(n^2) O(n2),其中 n n n 是二叉树的结点数。每个结点都被访问一次,最坏情况下每次将路径添加到结果中的时间是 O ( n ) O(n) O(n),因此总时间复杂度是 O ( n 2 ) O(n^2) O(n2)。
-
空间复杂度: O ( n ) O(n) O(n),其中 n n n 是二叉树的结点数。空间复杂度主要是哈希表和队列空间,哈希表需要存储每个结点的父结点,需要 O ( n ) O(n) O(n) 的空间,两个队列内元素个数都不超过 n n n。注意返回值不计入空间复杂度。
相关文章:

二叉树题目:路径总和 II
文章目录 题目标题和出处难度题目描述要求示例数据范围 前言解法一思路和算法代码复杂度分析 解法二思路和算法代码复杂度分析 题目 标题和出处 标题:路径总和 II 出处:113. 路径总和 II 难度 4 级 题目描述 要求 给你二叉树的根结点 root \tex…...

Qt model/view 理解01
在 Qt 中对数据处理主要有两种方式:1)直接对包含数据的的数据项 item 进行操作,这种方法简单、易操作,现实方式单一的缺点,特别是对于大数据或在不同位置重复出现的数据必须依次对其进行操作,如果现实方式改…...

c与c++中的字符串
在c中,string本质上是一个类; string与char *有些区别: char*是一个指针;string是一个类,类内封装了char*,管理这一个字符串,是一个char*的容器 在使用string类型时,要加上其头文…...
Android 获取IP地址的Ping值 NetworkPingUtils
项目里需要对动态配置的Ip列表都去ping下延迟,取出其中最小的三个进行随机取值然后去连接,倒腾了一下午终于搞出来了! 需求实现思路: 1.找到方法去ping IP地址; 2.同时去Ping,不能让用户等待;…...
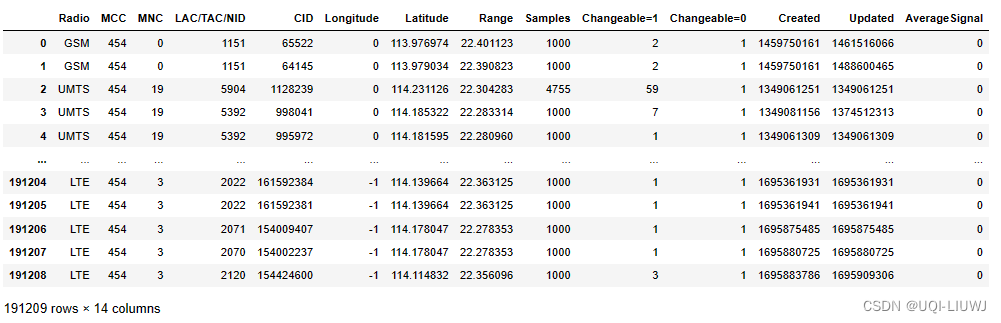
数据集笔记:OpenCelliD(手机基站开放数据库)
下载数据的方式可见:【数据获取】全球最大手机基站开源数据库 1 读取数据 import pandas as pdpd.read_csv(C:/Users/16000/Downloads/454.csv/454.csv,headerNone,names[radio,mcc,net,area,cell,unit,lon,lat,range,samples,changeable1,created1,updated,AveSi…...

Windows电脑多开器的使用心得分享
Windows电脑多开器是一种非常实用的软件工具,它可以让我们在同一个电脑上同时运行多个不同的应用程序,从而提高我们的工作和学习效率。以下是我在使用Windows电脑多开器时的一些心得分享: 确保你的电脑配置足够强大 多开软件需要消耗大量的…...
Android Studio实现简易计算器(带横竖屏,深色浅色模式,更该按钮颜色,selector,style的使用)
目录 前言 运行结果: 运行截屏(p50e) apk文件 源码文件 项目结构 总览 MainActivity.java drawable 更改图标的方法: blackbutton.xml bluebuttons.xml greybutton.xml orangebuttons.xml whitebutton.xml layout 布…...
虚拟机通过nat模式端口映射实现内网穿透
虚拟机通过nat模式端口映射实现内网穿透 1.网络状态 windows虚拟主机的IP为局域网的私有IP192.168.1.7linux的虚拟主机IP为nat的172.36.4.1062.linux修改nat模式的端口映射 3.windows宿主机防火墙添加规则,(或者直接关闭公共网络防火墙,不安全…...

计算机网络(六):应用层
参考引用 计算机网络微课堂-湖科大教书匠计算机网络(第7版)-谢希仁 1. 应用层概述 应用层是计算机网络体系结构的最顶层,是设计和建立计算机网络的最终目的,也是计算机网络中发展最快的部分 早期基于文本的应用 (电子邮件、远程登…...
Sublime Text 4 for Mac激活下载
Sublime Text for Mac是一款适用于Mac平台的文本编辑器。它具有快速的性能和丰富的功能,可以帮助用户快速进行代码编写和文本编辑。 软件下载:Sublime Text 4 for Mac激活下载 该软件具有直观的界面和强大的功能,包括多行选择、代码折叠、自动…...
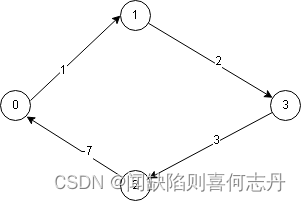
存在负权边的单源最短路径的原理和C++实现
负权图 此图用朴素迪氏或堆优化迪氏都会出错,floyd可以处理。 负环图 但floyd无法处理负权环,最短距离是无穷小。在环上不断循环。 经过k条边的最短距离(可能有负权变) 贝尔曼福特算法(bellman_ford)就是解决此问题的。 原理 …...
15-自动化测试——理论知识
目录 1.什么是自动化测试? 2.常见的自动化测试分类 2.1.单元测试(Java、Python) 2.2.接口测试(Java、Python) 2.3.UI测试(移动端、网站) 3.如何实施自动化测试? 4.自动化测试…...
学信息系统项目管理师第4版系列17_干系人管理
1. 项目经理和团队管理干系人的能力决定着项目的成败 2. 干系人满意度应作为项目目标加以识别和管理 3. 发展趋势和新兴实践 3.1. 识别所有干系人,而非在限定范围内 3.2. 确保所有团队成员都涉及引导干系人参与的活 3.3. 定期审查干系人群体,可与单…...

专业PDF编辑阅读工具PDF Expert mac中文特点介绍
PDF Expert mac是一款专业的PDF编辑和阅读工具。它可以帮助用户在Mac、iPad和iPhone等设备上查看、注释、编辑、填写和签署PDF文档。 PDF Expert mac软件特点 PDF编辑:PDF Expert提供了丰富的PDF编辑功能,包括添加、删除、移动、旋转、缩放、裁剪等操作…...
处理机调度的概念,层次联系以及七状态模型
1.基本概念 当有一堆任务要处理,但由于资源有限,这些事情没法同时处理。 这就需要确定某种规则来决定处理这些任务的顺序,这就是“调度”研究的问题。 2. 三个层次 1.高级调度(作业调度) 高级调度(作业…...
PS 图层剪贴蒙版使用方法
好 我们先打开PS软件 后面我们需要接触图框工具 在学习图框工具之前 先要掌握剪贴蒙版 这里 我们先点击左上角文件 然后选择新建 我们先新建一个画布出来 然后 我们点击 箭头指向处 新建一个空白图层 点击之后 会就多出一个空白图层 我们在这里 找到 矩形选框工具 然后 …...

总结1008
今日有些小摆烂,在家学习的日子,确实感觉不如在学校好,无论是在时间上,还是在效率上。在家复习效果因人而异吧,都到这个关键阶段了,可不能掉链子啊,明天势必要拿出100%的状态,心静不…...

软件工程从理论到实践客观题汇总(头歌第九章至第十七章)
九、软件体系结构设计 1、软件体系结构设计概述 2、软件体系结构模型的表示方法 3、软件体系结构设计过程 4、设计初步的软件体系结构 5、重用已有软件资源 6、精化软件体系结构 7、设计软件部署模型 8、文档化和评审软件体系结构设计 十、软件用户界面设计 1、用户界面设计概…...
ubuntu与win之间共享文件夹
ubuntu上设置共享文件夹 第一步:点击【设置】或【虚拟机弹窗下面的【设置】选项】 第二步:进入【虚拟机设置】页面,点击【选项】如下图所示 第三步:启用共享文件:点击【总是启用】第四步:添加共享文件&…...

flink处理函数--副输出功能
背景 在flink中,如果你想要访问记录的处理时间或者事件时间,注册定时器,或者是将记录输出到多个输出流中,你都需要处理函数的帮助,本文就来通过一个例子来讲解下副输出 副输出 本文还是基于streaming-with-flink这本…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...
