【洛谷 P1216】[USACO1.5] [IOI1994]数字三角形 Number Triangles 题解(动态规划)
[USACO1.5] [IOI1994]数字三角形 Number Triangles
题目描述
观察下面的数字金字塔。
写一个程序来查找从最高点到底部任意处结束的路径,使路径经过数字的和最大。每一步可以走到左下方的点也可以到达右下方的点。

在上面的样例中,从 7 → 3 → 8 → 7 → 5 7 \to 3 \to 8 \to 7 \to 5 7→3→8→7→5 的路径产生了最大权值。
输入格式
第一个行一个正整数 r r r ,表示行的数目。
后面每行为这个数字金字塔特定行包含的整数。
输出格式
单独的一行,包含那个可能得到的最大的和。
样例 #1
样例输入 #1
5
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5
样例输出 #1
30
提示
【数据范围】
对于 100 % 100\% 100% 的数据, 1 ≤ r ≤ 1000 1\le r \le 1000 1≤r≤1000,所有输入在 [ 0 , 100 ] [0,100] [0,100] 范围内。
题目翻译来自NOCOW。
USACO Training Section 1.5
IOI1994 Day1T1
思路
,使用一个二维数组 a 存储数字三角形的值,使用一个二维数组 dp 存储从顶点到每个位置的最大路径和。
状态转移方程:
dp[i][j] = max(dp[i - 1][j - 1], dp[i - 1][j]) + a[i][j];
在初始化 dp 数组时,dp[0][0] 赋值为 0。
在每次状态转移时,判断上一行的相邻两个位置的最大值,加上当前位置的值,得到当前位置的最大路径和。
最后,遍历最后一行的所有位置,取最大值即可。
AC代码
#include <iostream>
#include <algorithm>
#define AUTHOR "HEX9CF"
using namespace std;const int N = 1e3 + 5;int r;
int ans;
int a[N][N];
int dp[N][N];int main()
{cin >> r;for (int i = 1; i <= r; i++){for (int j = 1; j <= i; j++){cin >> a[i][j];}}dp[0][0] = 0;for (int i = 1; i <= r; i++){for (int j = 1; j <= i; j++){dp[i][j] = max(dp[i - 1][j - 1], dp[i - 1][j]) + a[i][j];}}ans = 0;for (int j = 1; j <= r; j++){// cout << dp[r][j] << endl;ans = max(ans, dp[r][j]);}cout << ans << endl;return 0;
}
相关文章:

【洛谷 P1216】[USACO1.5] [IOI1994]数字三角形 Number Triangles 题解(动态规划)
[USACO1.5] [IOI1994]数字三角形 Number Triangles 题目描述 观察下面的数字金字塔。 写一个程序来查找从最高点到底部任意处结束的路径,使路径经过数字的和最大。每一步可以走到左下方的点也可以到达右下方的点。 在上面的样例中,从 7 → 3 → 8 →…...
十四天学会C++之第四天(面向对象编程基础)
类和对象是什么? 在C中,类是一种用户定义的数据类型,它可以包含数据成员(也就是属性)和成员函数(也就是方法)。类是一种模板或蓝图,用于创建具体的对象。 对象是类的实例ÿ…...

复习Day09:哈希表part02:141.环形链表、142. 环形链表II、454.四数相加II、383赎金信
之前的blog:https://blog.csdn.net/weixin_43303286/article/details/131765317 我用的方法是在leetcode再过一遍例题,明显会的就复制粘贴,之前没写出来就重写,然后从拓展题目中找题目来写。辅以Labuladong的文章看。然后刷题不用…...

Internet通过TCP/IP协议可以实现多个网络的无缝连接
Internet通过TCP/IP(Transmission Control Protocol/Internet Protocol,传输控制协议/互联网协议)协议实现多个网络的无缝连接。 TCP/IP是Internet的基础通信协议套件,它定义了数据如何在不同网络之间传输和路由,使得…...

互联网Java工程师面试题·Dubbo 篇·第二弹
目录 18、Dubbo 用到哪些设计模式? 19、Dubbo 配置文件是如何加载到 Spring 中的? 20、Dubbo SPI 和 Java SPI 区别? 21、Dubbo 支持分布式事务吗? 22、Dubbo 可以对结果进行缓存吗? 23、服务上线怎么兼容旧版本&…...
(c语言)经典bug
#include<stdio.h> //经典bug int main() { int i 0; int arr[10] {1,2,3,4,5,6,7,8,9,10}; for (i 0; i < 12; i) //越界访问 { arr[i] 0; printf("hehe\n"); } return 0; } 注:输出结果为死循…...
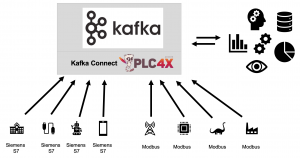
用于工业物联网和自动化的 Apache Kafka、KSQL 和 Apache PLC4
由于单一系统和专有协议,数据集成和处理是工业物联网(IIoT,又名工业 4.0 或自动化工业)中的巨大挑战。Apache Kafka、其生态系统(Kafka Connect、KSQL)和 Apache PLC4X 是以可扩展、可靠和灵活的方式实现端…...

1.1.1开发基础-硬件-万用表
1 万用表 万用表又叫多用表、三用表、复用表,是一种多功能、多量程的测量仪表,一般万用表可测量直流电流、直流电压、交流电压、电阻和音频电平等,有的还可以测交流电流、电容量、电感量及半导体的一些参数,是最常用、最简单的测试设备。 万用表是一种多功能多量程的便…...

Mysql内置函数、复合查询和内外连笔记
目录 一、mysql内置函数 1.1.日期函数 1.2.字符串函数 1.3.数学函数 1.4.其他函数 二、复合查询 2.2 自连接 2.3 子查询 2.3.1单行自查询 2.3.2 多行子查询 2.3.3 多列子查询 2.3.4在from子句中使用子查询 2.3.5合并查询 三、表的内连和外连 3.1内连接 3.2外连接…...
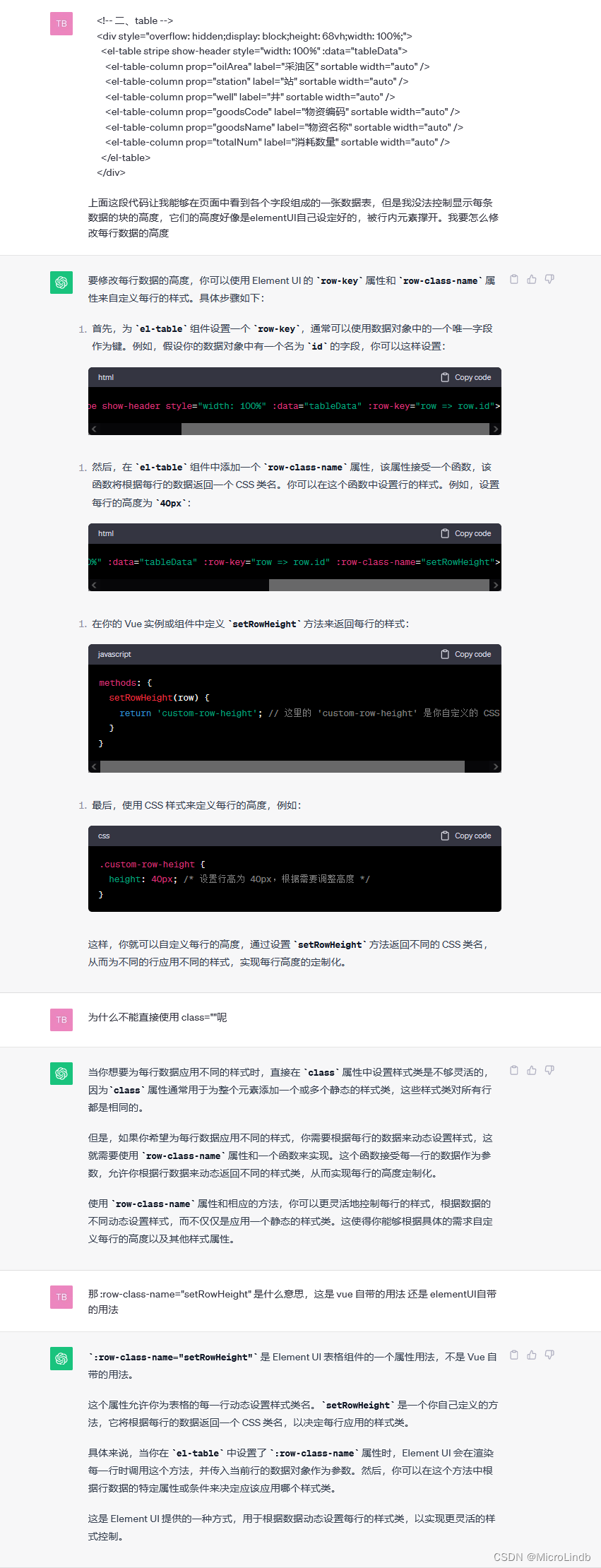
【VUE·疑难问题】定义 table 中每行的高度(使用 element-UI)
一、如何定义 table 中每一行的 height ? 1.table例子 <!-- 二、table --><div style"overflow: hidden;display: block;height: 68vh;width: 100%;"><el-table stripe show-header style"width: 100%" :data"tableData&q…...
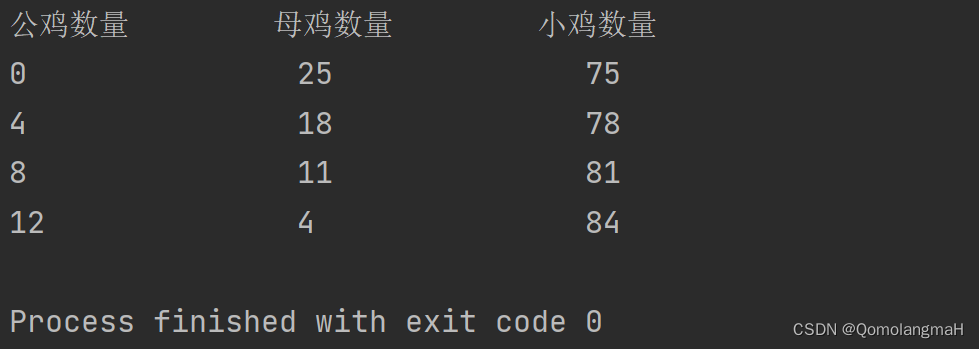
【重拾C语言】四、循环程序设计(后判断条件循环、先判断条件循环、多重循环;典例:计算平均成绩、打印素数、百钱百鸡问题)
目录 前言 四、循环程序设计 4.1 计算平均成绩——循环程序 4.1.1 后判断条件的循环 a. 语法 b. 典例 4.1.2 先判断条件的循环 a. 语法 b. 典例 4.1.3 for语句 a. 语法 b. 典例 4.2 计算全班每人平均成绩—多重循环 4.2.1 打印100以内素数 4.2.2 百钱百…...

Linux 安装 Gitlab
1、到官网下载Gitlab安装包 (如果是Centos,到el目录下载)。下载GitLab 2、安装依赖软件 sudo yum install -y policycoreutils-python3、安装gitlab sudo rpm -i gitlab-jh-16.3.4-jh.0.el7.x86_64.rpm 4、修改 gitlab.rb sudo vi /etc/gitlab/gitlab.rb 5、g…...
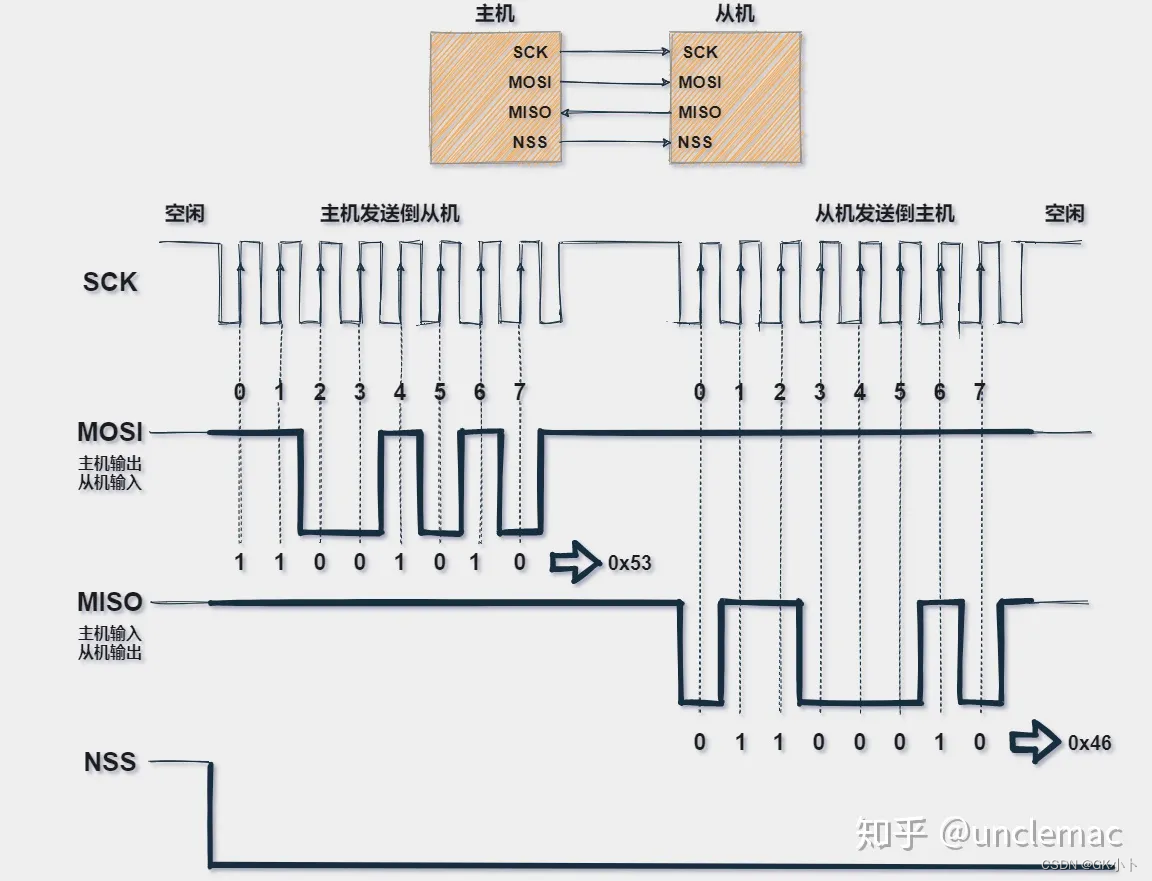
stm32-SPI协议
SPI协议详解(图文并茂超详细) SPI通讯协议 于是我们想有没有更好一点的串行通讯方式;相比较于UART,SPI的工作方式略有不同。 SPI是一个同步的数据总线,也就是说它是用单独的数据线和一个单独的时钟信号来保证发送端和…...
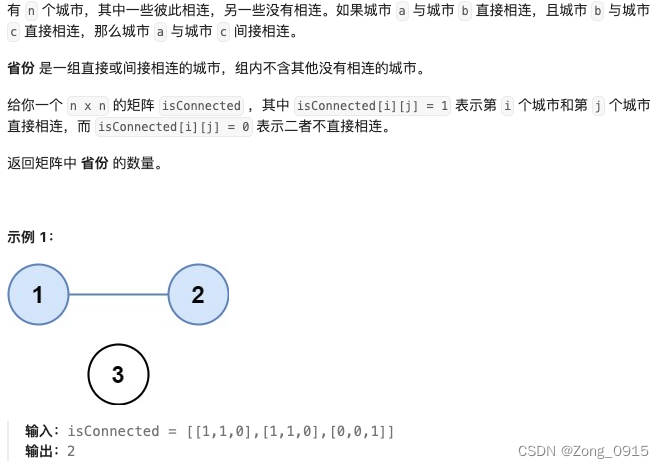
想要精通算法和SQL的成长之路 - 并查集的运用和案例(省份数量)
想要精通算法和SQL的成长之路 - 并查集的运用 前言一. 并查集的使用和模板1.1 初始化1.2 find 查找函数1.3 union 合并集合1.4 connected 判断相连性1.5 完整代码 二. 运用案例 - 省份数量 前言 想要精通算法和SQL的成长之路 - 系列导航 一. 并查集的使用和模板 先说一下并查集…...

解决内网拉取企微会话存档代理问题的一种办法
问题:客户的服务都是内网的,不能直接访问外网;访问外网的话需要走kong网关才能出去。 会话存档官网说可以使用socket5、http方式拉取会话存档;我这边尝试了直接使用kong网关的ip和端口配置进去,是访问不了的 我后面就…...

二十二,加上各种贴图
使用pbr的各种贴图,albedo,金属度,ao,法线,粗糙度,可以更好的控制各个片元 1,先加上纹理坐标 texCoords->push_back(osg::Vec2(xSegment, ySegment)); geom->setVertexAttribArray(3, texCoords, osg::Array::BI…...

新版校园跑腿独立版小程序源码 多校版本,多模块,适合跑腿,外卖,表白,二手,快递等校园服务
最新校园跑腿小程序源码 多校版本,多模块,适合跑腿,外卖,表白,二手,快递等校园服务 此版本为独立版本,不需要** 直接放入就可以 需要自己准备好后台的服务器,已认证的小程序…...
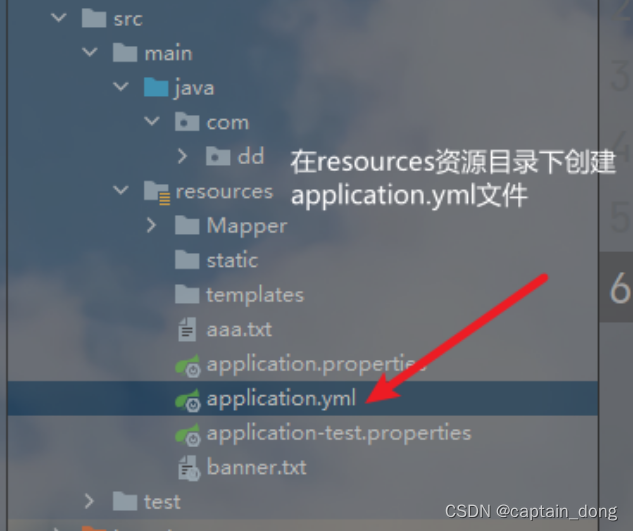
SpringBoot banner 样式 自动生成
目录 SpringBoot banner 样式 自动生成 图案网站: 1.第一步创建banner.txt文件 2.访问网站Ascii艺术字实现个性化Spring Boot启动banner图案,轻松修改更换banner.txt文件内容,收集了丰富的banner艺术字和图,并且支持中文banner下…...
回收站里面删除的照片如何恢复?
现在拍照已经成为人们生活中的一种方式,照片为我们保留了许多珍贵而美好的回忆。大家通常会把重要的照片保存在硬盘里,但当不小心把照片移入回收站并彻底删除时,情况就有点糟糕了。那么,回收站里删除的照片还有办法恢复吗…...

Qt model/view 理解 2
这是我对 Qt 的 model/view 内容理解的第二篇 blog,在第一篇文章中,介绍 QTableView 和 QAbstractTableModel,实现显示了对数据源的显示,但是显示的格式和修改的模式都是按照 View 控件的自显示方式。在此,使用 Qt 自带…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...
