机器学习 面试/笔试题(更新中)
1. 生成模型 VS 判别模型
生成模型:
由数据学得联合概率分布函数 P ( X , Y ) P(X,Y) P(X,Y),求出条件概率分布 P ( Y ∣ X ) P(Y|X) P(Y∣X)的预测模型。
朴素贝叶斯、隐马尔可夫模型、高斯混合模型、文档主题生成模型(LDA)、限制玻尔兹曼机。
判别式模型:
由数据直接学习决策函数 Y = f ( X ) Y=f(X) Y=f(X),或由条件分布概率 P ( Y ∣ X ) P(Y|X) P(Y∣X)作为预测模型。
K近邻、SVM、决策树、感知机、线性判别分析(LDA)、线性回归、传统的神经网络、逻辑斯蒂回归、boosting、条件随机场。
2. 线性回归
原理:用线性函数拟合数据,用 MSE 计算损失,然后用梯度下降法(GD)找到一组使 MSE 最小的权重。
3. 什么是回归?哪些模型可用于解决回归问题?
指分析因变量和自变量之间关系。
线性回归: 对异常值非常敏感;
多项式回归: 如果指数选择不当,容易过拟合;
岭回归:加入L2正则项,等价于对参数 w w w引入协方差为 α \alpha α的零均值高斯先验,不能做variable selection;
Lasso回归:加入L1正则项,等价于对参数 w w w引入拉普拉斯先验,可以做variable selection;弹性网络回归。
4. 梯度下降法找到的一定是下降最快的方向吗?
不一定,它只是目标函数在当前的点的切平面上下降最快的方向。
在实际执行期中,牛顿方向(考虑海森矩阵)才一般被认为是下降最快的方向,可以达到超线性的收敛速度。梯度下降类的算法的收敛速度一般是线性甚至次线性的(在某些带复杂约束的问题)。
5. 逻辑回归
是一中常见的用于分类的模型,本质上还是一个线性回归,先把特征线性组合,然后使用sigmoid函数(单调可微)将结果约束到0~1之间,结果用于二分类或者回归预测。
6. 逻辑回归和最大似然有什么关系?
通过极大似然法可以求解逻辑回归模型中的参数。最大似然估计就是通过已知结果去反推最大概率导致该结果的参数。极大似然估计是概率论在统计学中的应用,它提供了一种给定观察数据来评估模型参数的方法,即 “模型已定,参数未知”,通过若干次试验,观察其结果,利用实验结果得到某个参数值能够使样本出现的概率为最大,则称为极大似然估计。逻辑回归是一种监督式学习,是有训练标签的,就是有已知结果的,从这个已知结果入手,去推导能获得最大概率的结果参数 β \beta β,只要我们得出了这个参数,那我们的模型就自然可以很准确的预测未知的数据了。
7. 逻辑回归的损失函数;为什么不用MSE作为损失函数?
L o s s = − y log ( y ^ ) − ( 1 − y ) log ( 1 − y ^ ) Loss =-y\log(\hat{y})-(1-y)\log(1-\hat{y}) Loss=−ylog(y^)−(1−y)log(1−y^)
原因:
- 损失函数的角度:逻辑回归预测函数是非线性的,采用MSE得到的损失函数是非凸函数,会存在很多局部极小值,梯度下降法可能无法获得全局最优解。
- 极大似然的角度:采用极大似然法估计逻辑回归模型的参数,最终得到的对数似然函数形式与对数损失函数一致。
8. 逻辑回归中样本不均衡我们怎么处理?
- 调整分类阈值,不统一使用0.5,根据样本中类别的比值进行调整。
- 多类样本负采样。进一步也可将多类样本负采样构建多个训练集,最后聚合多个模型的结果。
- 少类样本过采样:随机复制、基于聚类的过采样、SMOTE。
- 改变性能指标,推荐采用ROC、AUC、F1-Score。
- 模型训练增加正负样本惩罚权重,少类样本权重加大,增大损失项。
9. 逻辑回归模型是线性模型还是非线性,为什么?能推导它的原理吗?
逻辑回归模型是广义线性模型,但其原始形式是非线性的,决定这个复合函数是否是线性的,要看 g ( x ) g(x) g(x)的形式,假如阈值为 0.5,那么 g ( x ) > = 0 g(x)>=0 g(x)>=0时,预测为 1,否则预测为 0.因此,这里的$ g(x)$,实际是一个决策面,这个决策面的两侧分别是正例和负例。逻辑回归的作用是把决策面两侧的点映射到逻辑回归曲线阈值的两侧。
10. 逻辑回归如何解决非线性分类问题?
加核函数或特征变换,显式地把特征映射到高维空间。
11. 逻辑回归使用注意事项,相比别的分类模型为什么使用它?
注意,建模数据量不能太少,目标变量中每个类别所对应的样本数量要足够充分,才能支持建模排除共线性问题(自变量间相关性很大);异常值会给模型带来很大干扰,要剔除;逻辑回归不能处理缺失值,所以之前应对缺失值进行适当处理。
相对于别的模型用逻辑回归的好处是在于在数据量比较大的情况下越复杂的模型可能会越慢,逻辑回归就显得会快上很多了。
12. LR 和 DNN 联系和区别是什么?
二者都是用于二分类问题,且无法学习比较复杂的非线性模型,区别在于DNN 是神经网络,输出结果为 ( 1 , − 1 ) (1,-1) (1,−1),lr 输出结果为 (0,1);DNN 的激活函数为sign,lr 的激活函数为 sigmoid。
13. LR逻辑回归为什么对特征进行离散化?
-
离散特征的增加和减少都很容易,易于模型的快速迭代;
-
稀疏向量内积乘法运算速度快,计算结果方便存储,容易扩展;
-
离散化后的特征对异常数据有很强的鲁棒性:比如一个特征是年龄>30是1,否则0。如果特征没有离散化,一个异常数据“年龄300岁”会给模型造成很大的干扰;
-
逻辑回归属于广义线性模型,表达能力受限;单变量离散化为N个后,每个变量有单独的权重,相当于为模型引入了非线性,能够提升模型表达能力,加大拟合;
-
离散化后可以进行特征交叉,由 M + N M+N M+N个变量变为 M × N M\times N M×N个变量,进一步引入非线性,提升表达能力;
-
特征离散化后,模型会更稳定,比如如果对用户年龄离散化,20-30作为一个区间,不会因为一个用户年龄长了一岁就变成一个完全不同的人。当然处于区间相邻处的样本会刚好相反,所以怎么划分区间是门学问;
-
特征离散化以后,起到了简化了逻辑回归模型的作用,降低了模型过拟合的风险。
14. 谈谈牛顿法
收敛速度快,指数级收敛,但是不保证线性收敛,只保证二阶导收敛。
牛顿法比梯度下降法收敛的要快,这是因为牛顿法是二阶收敛,梯度下降是一阶收敛。事实上,梯度下降法每次只从当前位置选一个上升速度最大的方向走一步,牛顿法在选择方向时,不仅会考虑上升速度是否够大,还会考虑你走了一步之后,上升速度是否会变得更大。,所以所需要的迭代次数更少。从几何上说,牛顿法就是用一个二次曲面去拟合你当前所处位置的局部曲面,而梯度下降法是用一个平面去拟合当前的局部曲面,通常情况下,二次曲面的拟合会比平面更好,所以牛顿法选择的下降路径会更符合真实的最优下降路径。
15. 牛顿法优化过程
牛顿法的基本思想是用迭代点的梯度信息和二阶导数对目标函数进行二次函数逼近,然后把二次函数的极小值作为新的迭代点,并不断重复这一过程,直到求出极小点。
假设 f ( x ) f(x) f(x)的二阶导数 ∇ 2 f ( x ) \nabla^2f(x) ∇2f(x)连续,函数 f ( x ) f(x) f(x)在 x k x_k xk处的二阶泰勒展开为
f ( x ) ≈ f k + ∇ f ( x k ) ( x − x k ) + 1 2 ( x − x k ) T ∇ 2 f ( x k ) ( x − x k ) f(x) \approx f_k +\nabla f(x_k)(x- x_k)+\frac 12 (x-x_k)^T\nabla ^2f(x_k)(x-x_k) f(x)≈fk+∇f(xk)(x−xk)+21(x−xk)T∇2f(xk)(x−xk)
其中 f k : = f ( x k ) f_k:=f(x_k) fk:=f(xk),求函数的驻点那就是求导并令导数为0,即
∇ f ( x ) = ∇ f ( x k ) + ∇ 2 f ( x k ) ( x − x k ) = 0 \nabla f(x)=\nabla f(x_k)+\nabla ^2f(x_k)(x-x_k)=0 ∇f(x)=∇f(xk)+∇2f(xk)(x−xk)=0
如果二阶导数为非奇异,可以得到下一个迭代点(上式求出来的 x x x就是 x k + 1 x_{k+1} xk+1
x k + 1 = x k − ∇ 2 f ( x k ) ∇ f ( x k ) x_{k+1}=x_k-\nabla^2f(x_k)\nabla f(x_k) xk+1=xk−∇2f(xk)∇f(xk)
如果二阶导数奇异,那么可以求解下面线性方程确定搜索方向 d k d_k dk
∇ 2 f ( x k ) d k = − ∇ f ( x k ) \nabla^2f(x_k)d_k=-\nabla f(x_k) ∇2f(xk)dk=−∇f(xk)
后计算下一个迭代点 x k + 1 = x k + d k x_{k+1}=x_k +d_k xk+1=xk+dk
16. 交叉熵的物理含义
交叉熵是由相对熵导出的,相对熵的含义是衡量两个概率分布 p p p 与 q q q 之间的差异。相对熵的前半部分是交叉熵,后半部分是常数,相对熵达到最小值的时候,交叉熵也达到了最小值,所以交叉熵也可以衡量计算之后的概率分布 q q q 与真实概率分布 p p p 之间的差异。交叉熵最小值等同于最大似然估计。
17. SVM
机器学习之SVM
SVM 是一种二分类模型,学习的目标是在特征空间中找到一个分离超平面,且此超平面是间隔最大化的最优分离超平面,最终可转化为一个凸二次规划问题求解。(间隔最大是它有别于感知机)
(1)当训练样本线性可分时,通过硬间隔最大化,学习一个线性分类器,即线性可分支持向量机;
(2)当训练数据近似线性可分时,引入松弛变量,通过软间隔最大化,学习一个线性分类器,即线性支持向量机;
(3)当训练数据线性不可分时,通过使用核技巧及软间隔最大化,学习非线性支持向量机。
注:以上各SVM的数学推导应该熟悉:硬间隔最大化(几何间隔)—学习的对偶问题—软间隔最大化(引入松弛变量)— 非线性支持向量机(核技巧)
18. SVM,LR 的区别联系,重点介绍下 SVM 算法。
- 相同之处:如果不考虑核函数,LR和SVM都是线性分类器,都是监督算法,都是判别模型。
- 不同之处:1.损失函数不同,LR使用logistical loss(交叉熵),SVM使用hingeloss,SVM的损失函数自带正则项,而LR则需要自己添加正则项;2.解决非线性问题时,SVM采用核函数机制,而LR一般不用,因为复杂核函数需要很大计算量,SVM中只有支持向量参与计算,而LR是全部样本都需要参与计算,若使用核函数计算量太大。3.对异常值的敏感度不一样。LR中所有样本都对分类平面有影响,所以异常点的影响会被掩盖。但SVM的分类平面取决于支持向量,如果支持向量受到异常值影响,则结果难以预测。4.在高维空间LR的表现比SVM更稳定,因为SVM是要最大化间隔,这个间隔依赖与距离测度,在高维空间时这个距离测度往往不太好。(所以需要做归一化)
假设:特征数量为 n n n,训练样本数量为 m m m
1)如果 n n n相对于 m m m更大,比如 n = 10000 n=10000 n=10000, m = 1000 m=1000 m=1000,则使用LR或线性SVM
理由:特征数相对于训练样本数已经够大了,使用线性模型就能取得不错的效果,不需要过于复杂的模型。
2)如果 n n n 较小, m m m比较大,比如 n = 10 n = 10 n=10, m = 10 , 000 m = 10,000 m=10,000,则使用 SVM(高斯核函数)
理由:在训练样本数量足够大而特征数较小的情况下,可以通过使用复杂核函数的 SVM 来获得更好的预测性能,而且因为训练样本数量并没有达到百万级,使用复杂核函数的 SVM 也不会导致运算过慢。
3)如果 n n n 较小, m m m 非常大,比如 n = 100 n = 100 n=100, m = 500 , 000 m = 500,000 m=500,000,则应该引入/创造更多的特征,然后使用LR 或者线性核函数的 SVM。
理由::因为训练样本数量特别大,使用复杂核函数的 SVM 会导致运算很慢,因此应该考虑通过引入更多特征,然后使用线性核函数的 SVM 或者 LR来构建预测性更好的模型。
19. SVM 为什么采用间隔最大化?
当训练数据线性可分时,存在无穷个分离超平面可以将两类数据正确分开。感知机利用误分类最小策略,求得分离超平面,不过此时的解有无穷多个。线性可分支持向量机利用间隔最大化求得最优分离超平面,这时,解是唯一的。另一方面,此时的分隔超平面所产生的分类结果是最鲁棒的,对未知实例的泛化能力最强。可以借此机会阐述一下几何间隔以及函数间隔的关系。
20. 为什么 SVM 要引入核函数?
原始样本空间可能会线性不可分,这样需要将原始空间映射到一个更高维的特征空间,使得样本在这个特征空间线性可分。样本映射到高维空间后的内积求解通常是困难的,引入核函数可简化内积的计算。
21. 为什么SVM对缺失数据敏感?
这里说的缺失数据是指缺失某些特征数据,向量数据不完整。SVM 没有处理缺失值的策略。而 SVM 希望样本在特征空间中线性可分,所以特征空间的好坏对SVM的性能很重要。缺失特征数据将影响训练结果的好坏。
22. 核函数要满足什么性质,常见的核函数有哪些?
核函数的性质:核函数必须是连续的,对称的,并且最优选地应该具有正(半)定 Gram 矩阵。据说满足 Mercer 定理的核是正半定数,意味着它们的核矩阵只有非负特征值。使用肯定的内核确保优化问题将是凸的和解决方案将是唯一的。
然而,许多并非严格定义的核函数在实践中表现得很好。一个例子是 Sigmoid内核,尽管它广泛使用,但它对于其参数的某些值不是正半定的。 Boughorbel(2005)也实验证明,只有条件正定的内核在某些应用中可能胜过大多数经典内核。
内核还可以分为各向异性静止,各向同性静止,紧凑支撑,局部静止,非稳定或可分离非平稳。此外,内核也可以标记为 scale-invariant(规模不变)或scale-dependent(规模依赖),这是一个有趣的属性,因为尺度不变内核驱动训练过程不变的数据的缩放。
补充:Mercer定理:任何半正定的函数都可以作为核函数。所谓半正定的函数 f ( x i , x j ) f(x_i,x_j) f(xi,xj),是指拥有训练数据集合 ( x 1 , x 2 , … , x n ) (x_1,x_2,\dots,x_n) (x1,x2,…,xn),我们定义一个矩阵的元素 a i j = f ( x i , x j ) a_{ij}=f(x_i,x_j) aij=f(xi,xj),这个矩阵是 n × n n\times n n×n,如果这个矩阵式半正定的,那么 f ( x i , x j ) f(x_i,x_j) f(xi,xj)就称为半正定函数。这个 Mercer 定理不是核函数必要条件,只是一个充分条件,即还有不满足 mercer 定理的函数也可以是核函数。
几种常用的核:
- 线性核:线性内核是最简单的内核函数。它由内积 < x , y > <x,y> <x,y>加上可选的常数 c c c给出。使用线性内核的内核算法通常等于它们的非内核对应物,即具有线性内核的 KPCA与标准 PCA 相同。
- 多项式核函数:多项式核是非固定内核。 多项式内核非常适合于所有训练数据都归一化的问题。
- 高斯核:高斯核是径向基函数核的一个例子。可调参数 σ \sigma σ在内核的性能中起着主要作用,并且应该仔细地调整到手头的问题。 如果过高估计,指数将几乎呈线性,高维投影将开始失去其非线性功率。 另一方面,如果低估,该函数将缺乏正则化,并且决策边界将对训练数据中的噪声高度敏感。
- 指数的内核:指数核与高斯核密切相关,只有正态的平方被忽略。 它也是一个径向基函数内核。
- 拉普拉斯算子核:拉普拉斯核心完全等同于指数内核,除了对 σ \sigma σ参数的变化不那么敏感。作为等价的,它也是一个径向基函数内核。
23. SVM的高斯核为什么会把原始维度映射到无穷多维?
首先我们要清楚,SVM中,对于维度的计算,我们可以用内积的形式,假设函数 K ( x 1 , x 2 ) = ( 1 , x 1 x 2 , x 2 ) K(x_1,x_2)=(1,x_1x_2,x^2) K(x1,x2)=(1,x1x2,x2)表示一个简单的从二维映射到三维。则在SVM的计算中,可以表示为 K ( x 1 , x 2 ) = 1 + x 1 x 2 + x 2 K(x_1,x_2)=1+x_1x_2+x^2 K(x1,x2)=1+x1x2+x2.再来看 e x e^x ex泰勒展开式: e x ≈ 1 + x + x 2 2 ! + x 3 3 ! + ⋯ + x n n ! e^x \approx 1 + x + \frac{x^2}{2!} +\frac{x^3}{3!}+\dots+ \frac{x^n}{n!} ex≈1+x+2!x2+3!x3+⋯+n!xn 所以这个无穷多项的式子正是对于 e x e^x ex的近似, e x e^x ex所对应的映射: K ( x ) = ( 1 , x , x 2 2 ! , x 3 3 ! , … , x n n ! ) K(x)=(1,x, \frac{x^2}{2!}, \frac{x^3}{3!},\dots, \frac{x^n}{n!}) K(x)=(1,x,2!x2,3!x3,…,n!xn) 再来看高斯核: K ( x 1 , x 2 ) = e ( − ∥ x 1 − x 2 ∥ 2 2 σ 2 ) K(x_1,x_2)=e^{(-\frac{\lVert x_1-x_2\rVert^2}{2\sigma^2})} K(x1,x2)=e(−2σ2∥x1−x2∥2) 将泰勒展开式带入高斯核,我们得到了一个无穷维度的映射: K ( x 1 , x 2 ) = 1 + ( − ∥ x 1 − x 2 ∥ 2 2 σ 2 ) + ( − ∥ x 1 − x 2 ∥ 2 2 σ 2 ) 2 2 ! + ( − ∥ x 1 − x 2 ∥ 2 2 σ 2 ) 3 3 ! + ⋯ + ( − ∥ x 1 − x 2 ∥ 2 2 σ 2 ) n n ! K(x_1,x_2) = 1+(-\frac{\lVert x_1-x_2\rVert^2}{2\sigma^2}) +\frac{(-\frac{\lVert x_1-x_2\rVert^2}{2\sigma^2})^2}{2!}+\frac{(-\frac{\lVert x_1-x_2\rVert^2}{2\sigma^2})^3}{3!}+\dots+\frac{(-\frac{\lVert x_1-x_2\rVert^2}{2\sigma^2})^n}{n!} K(x1,x2)=1+(−2σ2∥x1−x2∥2)+2!(−2σ2∥x1−x2∥2)2+3!(−2σ2∥x1−x2∥2)3+⋯+n!(−2σ2∥x1−x2∥2)n
那么,对于 x 1 x_1 x1和 x 2 x_2 x2的内积形式符合在SVM中无穷维度下的内积计算,即高斯核将数据映射到无穷高的维度。
核函数的本质简要概括下:
- 实际中,我们会经常遇到线性不可分的样例,此时,我们的常用做法是把样例特征映射到高维空间去(映射到高维空间后,相关特征便被分开了,也就达到了分类的目的);
- 但进一步,如果凡是遇到线性不可分的样例,一律映射到高维空间,那么这个维度大小是会高到可怕(如19维乃至无穷维);
- 此时,核函数就隆重登场了,核函数的价值在于它虽然也是将特征进行从低维到高维的转换,但核函数绝就绝在它事先在低维上进行计算,而将实质上的分类效果表现在了高维上,也就如上文所说的避免了直接在高维空间中的复杂计算。
相关文章:
)
机器学习 面试/笔试题(更新中)
1. 生成模型 VS 判别模型 生成模型: 由数据学得联合概率分布函数 P ( X , Y ) P(X,Y) P(X,Y),求出条件概率分布 P ( Y ∣ X ) P(Y|X) P(Y∣X)的预测模型。 朴素贝叶斯、隐马尔可夫模型、高斯混合模型、文档主题生成模型(LDA)、限制玻尔兹曼机…...

【算法题】100019. 将数组分割成最多数目的子数组
插: 前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。点击跳转到网站。 坚持不懈,越努力越幸运,大家一起学习鸭~~~ 题目: 给你一个只包含 非负 整数的数组 n…...

commons-io工具类常用方法
commons-io是Apache Commons项目的一个模块,提供了一系列处理I/O(输入/输出)操作的工具类和方法。它旨在简化Java I/O编程,并提供更多的功能和便利性。 读取文件内容为字符串 String path"C:\\Users\\zhang\\Desktop\\myyii\…...
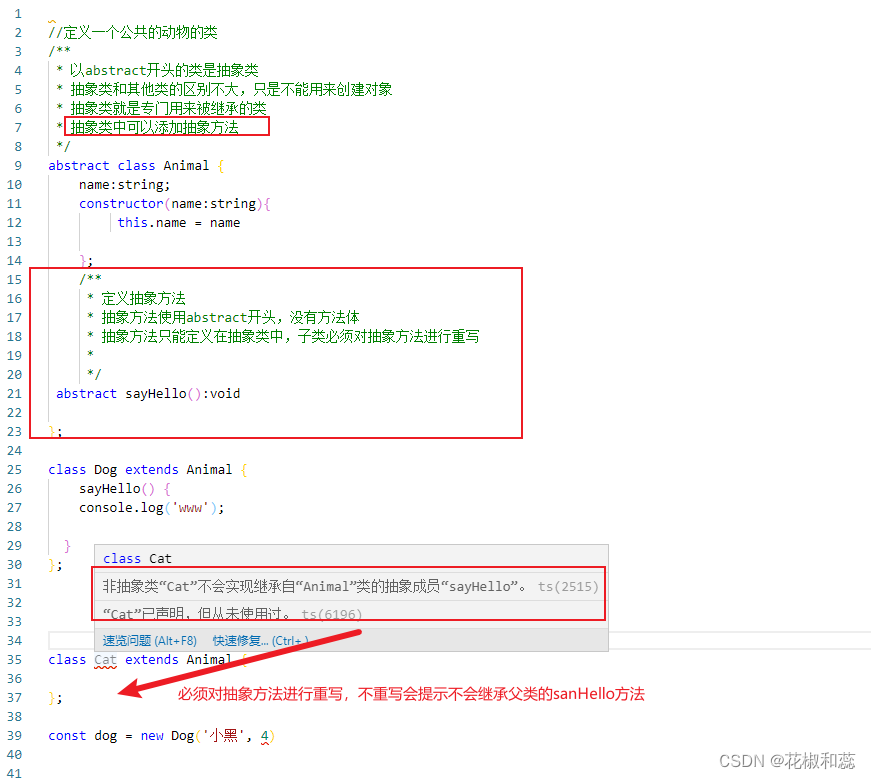
【Typescript】面向对象(上篇),包含类,构造函数,继承,super,抽象类
假期第七篇,对于基础的知识点,我感觉自己还是很薄弱的。 趁着假期,再去复习一遍 面向对象:程序中所有的操作都需要通过对象来完成 计算机程序的本质就是对现实事物的抽象,抽象的反义词是具体。比如照片是对一个具体的…...

【python】python中字典的用法记录
文章目录 序言1. 字典的创建和访问2. 字典如何添加元素3. 字典作为函数参数4. 字典排序 序言 总结字典的一些常见用法 1. 字典的创建和访问 字典是一种可变容器类型,可以存储任意类型对象 key : value,其中value可以是任何数据类型,key必须…...

基于Java的大学生心理咨询系统设计与实现(源码+lw+部署文档+讲解等)
文章目录 前言具体实现截图论文参考详细视频演示为什么选择我自己的网站自己的小程序(小蔡coding)有保障的售后福利 代码参考源码获取 前言 💗博主介绍:✌全网粉丝10W,CSDN特邀作者、博客专家、CSDN新星计划导师、全栈领域优质创作…...
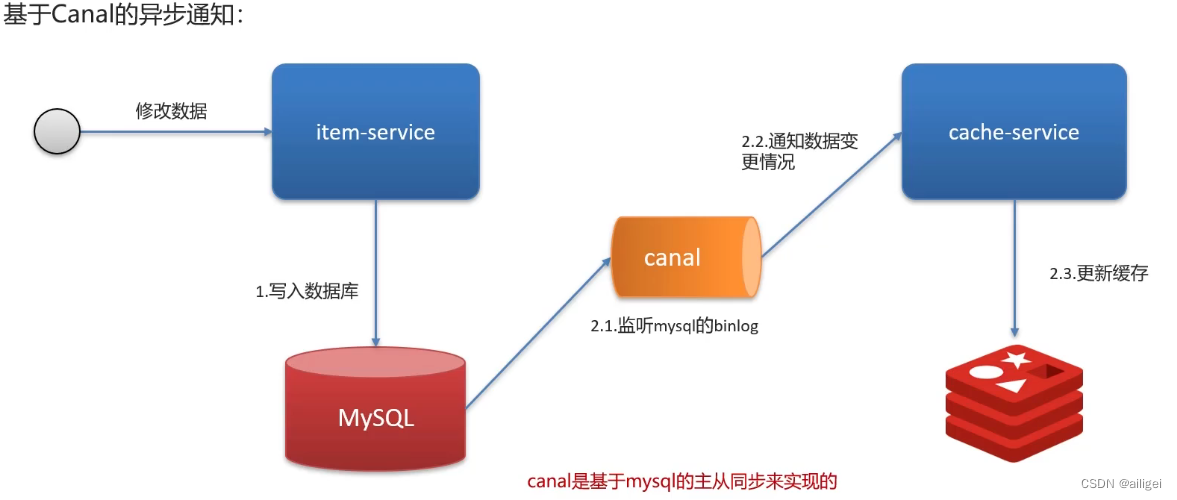
Redis-双写一致性
双写一致性 双写一致性解决方案延迟双删(有脏数据的风险)分布式锁(强一致性,性能比较低)异步通知(保证数据的最终一致性,高并发情况下会出现短暂的不一致情况) 双写一致性 当修改了数…...

CustomTkinter:创建现代、可定制的Python UI
文章目录 介绍安装设置外观与主题外观模式主题设置自定义主题颜色窗口缩放CTkFont字体设置CTkImage图片Widgets窗口部件CTk Windows窗口CTk窗口CTkInputDialog对话框CTkToplevel顶级窗口布局pack布局palce布局Grid 网格布局Frames 框架Frames滚动框架...

华为OD机试真题【不含 101 的数】
1、题目描述 【不含 101 的数】 【题目描述】 小明在学习二进制时,发现了一类不含 101的数,也就是: 将数字用二进制表示,不能出现 101 。 现在给定一个整数区间 [l,r] ,请问这个区间包含了多少个不含 101 的数&#…...

Spring IoC和DI详解
IOC思想 IoC( Inversion of Control,控制反转) 不是一门具体技术,而是一种设计思想, 是一种软件设计原则,它将应用程序的控制权(Bean的创建和依赖关系)从应用程序代码中解耦出来&am…...

mysql-binlog
1. 常用的binlog日志操作命令 1. 查看bin-log是否开启 show variables like log_%;2. 查看所有binlog日志列表 show master logs;3.查看master状态 show master status;4. 重置(清空)所有binlog日志 reset master;2. 查看binlog日志内容 1、使用mysqlb…...
通过BeanFactotyPostProcessor动态修改@FeignClient的path
最近项目有个需求,要在启动后,动态修改FeignClient的请求路径,网上找到的基本都是在FeignClient里使用${…},通过配置文件来定义Feign的接口路径,这并不能满足我们的需求 由于某些特殊原因,我们的每个接口…...

数据结构与算法系列-二分查找
二分查找 什么是二分查找? 二分查找是一种针对有序集合,每次将要查找的区间缩小一半,直到找到查找元素,或区间被缩小为0。 如何实现二分查找? 实现有3个注意点: 终止条件是 low < high 2.求中点的算…...

CSS 毛玻璃特效运用目录
主要是记录毛玻璃相关的特效实践案例和实现思路。 章节名称完成度难度文章地址完整代码下载地址Glassmorphism 登录表单完成一般文章链接代码下载Glassmorphism 按钮悬停效果完成一般文章链接代码下载Glassmorphism 计算器完成一般文章链接代码下载Glassmorphism 卡片悬停效果…...
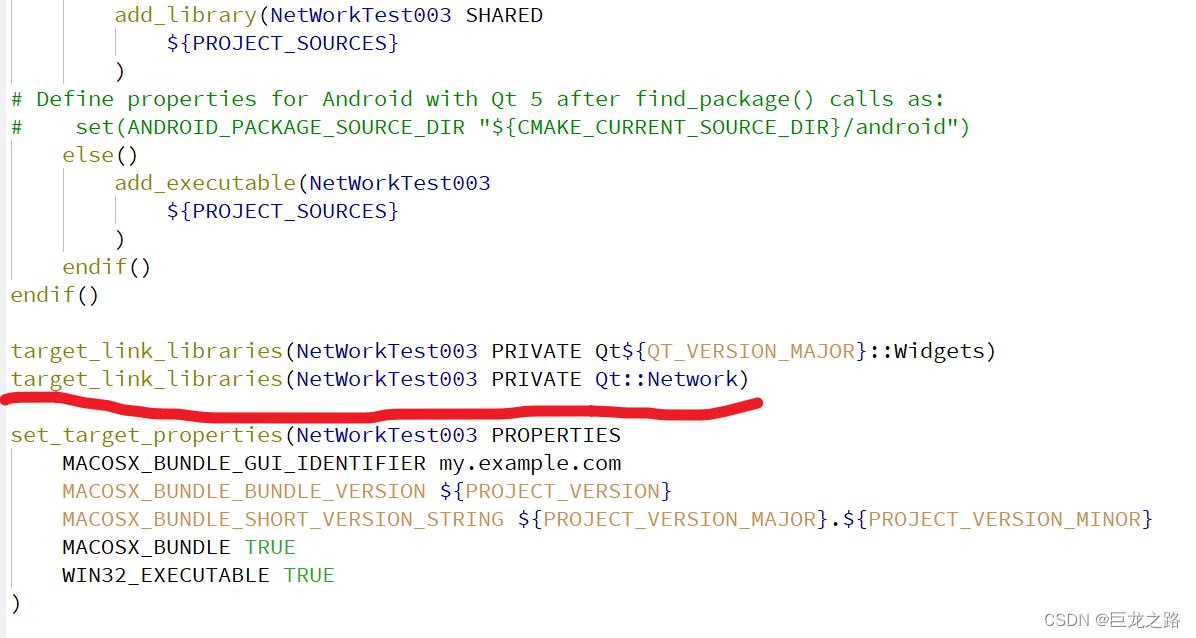
如何在Qt6中引入Network模块
2023年10月1日,周日凌晨 2023年10月2日,周一下午 第一次更新 目录 如果用的是CMakeQt Console ApplicationQt Widgets Application如果用的是qmake 如果用的是CMake find_package(Qt6 COMPONENTS Network REQUIRED) target_link_libraries(mytarget…...

2023/10/4 QT实现TCP服务器客户端搭建
服务器端: 头文件 #ifndef WIDGET_H #define WIDGET_H#include <QWidget> #include <QTcpServer> #include <QTcpSocket> #include <QList> #include <QMessageBox> #include <QDebug>QT_BEGIN_NAMESPACE namespace Ui { cla…...
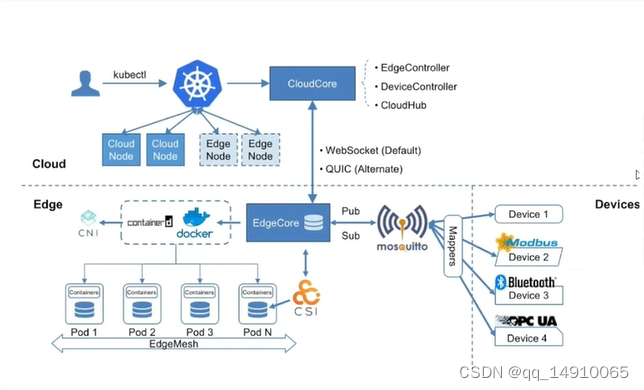
云原生边缘计算KubeEdge安装配置
1. K8S集群部署,可以参考如下博客 请安装k8s集群,centos安装k8s集群 请安装k8s集群,ubuntu安装k8s集群 2.安装kubEedge 2.1 编辑kube-proxy使用ipvs代理 kubectl edit configmaps kube-proxy -n kube-system #修改kube-proxy#大约在40多行…...
【LeetCode热题100】--35.搜索插入位置
35.搜索插入位置 使用二分查找: class Solution {public int searchInsert(int[] nums, int target) {int low 0,high nums.length -1;while(low < high){//注意每次循环完都要计算midint mid (low high)/2;if(nums[mid] target){return mid;}if(nums[mid]…...

mysql面试题13:MySQL中什么是异步复制?底层实现?
该文章专注于面试,面试只要回答关键点即可,不需要对框架有非常深入的回答,如果你想应付面试,是足够了,抓住关键点 面试官:讲一讲mysql中什么是异步复制?底层实现? MySQL中的异步复制(Asynchronous Replication)是一种复制模式,主服务器将数据写入二进制日志后,无…...
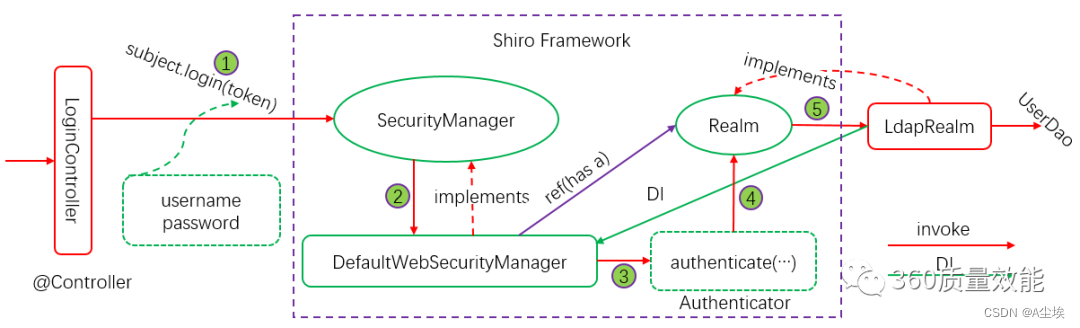
SpringBoot-Shiro安全权限框架
Apache Shiro是一个强大而灵活的开源安全框架,它干净利落地处理身份认证,授权,企业会话管理和加密。 官网: http://shiro.apache.org/ 源码: https://github.com/apache/shiro Subject:代表当前用户或…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...
中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...
