CYEZ 模拟赛 9
A
a ⊥ b ⇒ a − b ⊥ a b (1) a \perp b \Rightarrow a-b \perp ab \tag {1} a⊥b⇒a−b⊥ab(1)
证明: gcd ( a , b ) = gcd ( b , a − b ) \gcd(a,b) = \gcd(b, a-b) gcd(a,b)=gcd(b,a−b),故 a − b ⊥ b a - b \perp b a−b⊥b,同理 a − b ⊥ b a-b \perp b a−b⊥b,故 a − b ⊥ a b a-b \perp ab a−b⊥ab。
题目要求 a + b ∣ a b a+b \mid ab a+b∣ab,记 g = gcd ( a , b ) , a = x g , b = y g g = \gcd(a,b),a=xg, b = yg g=gcd(a,b),a=xg,b=yg。
x g + y g ∣ x y g 2 xg+yg \mid xyg^2 xg+yg∣xyg2,得 x + y ∣ x y g x+y \mid xyg x+y∣xyg。
由于 x ⊥ y x \perp y x⊥y,由 ( 1 ) (1) (1) 得 x + y ⊥ x y x + y \perp xy x+y⊥xy,得 x + y ∣ g x+y \mid g x+y∣g。
枚举 i = x + y i = x+y i=x+y,此时,根据 ( 1 ) (1) (1) 可得 x , y x,y x,y 的对数即为 φ ( i ) \varphi (i) φ(i),而 ( x + y ) g ≤ n (x+y)g \le n (x+y)g≤n 且 x + y ∣ g x+y \mid g x+y∣g,可能取值有 ⌊ n i 2 ⌋ \lfloor \frac{n}{i^2}\rfloor ⌊i2n⌋ 个。
x + y x+y x+y 的上界容易确定,为 n \sqrt n n。故答案为 ∑ i = 1 n φ ( i ) × ⌊ n i 2 ⌋ \sum_{i=1}^{\sqrt {n}} \varphi (i) \times \lfloor \frac{n}{i^2}\rfloor ∑i=1nφ(i)×⌊i2n⌋。
对于 φ \varphi φ 函数,考虑线筛时同时处理 φ \varphi φ。
#include<bits/stdc++.h>
#define int long long
using namespace std;const int N = 1e7 + 5;int n, p[N], phi[N], P[N], tot;bool v[N];signed main()
{ios::sync_with_stdio(0); cin.tie(0);cin >> n;int m = sqrt(n), ans = 0;for(int i=2; i<=m; i++){if(!v[i]){phi[i] = i-1;P[++tot] = i;}for(int j=1; i*P[j]<=m and j<=tot; j++){v[i*P[j]] = 1;if(i % P[j] == 0) {phi[i * P[j]] = phi[i] * P[j]; break;}else phi[i * P[j]] = phi[i] * (P[j] - 1);}ans += phi[i] * ((n / i) / i);}cout << ans;
}B
简单 LIS 题。
f i = max j < i , a j < a i f j + 1 f_i = \max_{j<i,a_j<a_i} f_j + 1 fi=j<i,aj<aimaxfj+1
容易用 BIT 优化。
#include<bits/stdc++.h>
#define pii pair <int, int>
#define int long long
using namespace std;const int mod = 123456789;const int N = 1e5 + 5;void chmax(int &A, int &B, int a, int b)
{if(a > A) A = a, B = b;else if(a == A) B += b, B %= mod;
}int n, type, a[N], f[N], g[N];int F[N], G[N];
int lowbit(int x){return x&(-x);}
void modify(int x, int val1, int val2)
{for(;x<=1e5; x+=lowbit(x)) chmax(F[x], G[x], val1, val2);
}
pii query(int x)
{int res1 = 0, res2 = 0; for(;x>0; x-=lowbit(x)) chmax(res1, res2, F[x], G[x]); return {res1, res2};
}signed main()
{ios::sync_with_stdio(0); cin.tie(0);cin >> n >> type;for(int i=1; i<=n; i++)cin >> a[i];int ansf = 0, ansg = 0;for(int i=1; i<=n; i++){f[i] = 1, g[i] = 1;auto res = query(a[i] - 1);chmax(f[i], g[i], res.first + 1, res.second);modify(a[i], f[i], g[i]);chmax(ansf, ansg, f[i], g[i]);}cout << ansf << "\n";if(type) cout << ansg;
}
C
记 b i / w i b_i/w_i bi/wi 为第 i i i 层的黑色 / 白色节点个数, s b i / s w i sb_i/sw_i sbi/swi 为前 i i i 层黑色 / 白色节点个数(均指白色节点作为根时)。在本题中,我们认为根节点深度为 1 1 1。
考虑分别处理 lca 为白色节点和黑色节点的点对:
对于 lca 为白点的点对,两者为祖先 / 后代的关系。距离为 i i i 的该类型点对数量为 s w n − i × w i + 1 sw_{n-i} \times w_{i+1} swn−i×wi+1,含义是 s w n − i sw_{n-i} swn−i 个节点可能作为祖先,考虑到子树本质相同的性质,对于每个祖先,有 w i + 1 w_{i+1} wi+1 个节点与其距离为 i i i。
对于 lca 为黑点的点对,两点一定分别在 lca 的黑白子树中,设白 / 黑子树内两点到 lca 距离分别为 i , j i,j i,j,则可能的点对个数为 w i × w j + 1 w_i \times w_{j+1} wi×wj+1,可能作为祖先的节点个数为 s b n − max ( i , j ) sb_{n-\max(i,j)} sbn−max(i,j)。
#include<bits/stdc++.h>
#define int long long
using namespace std;const int mod = 123456789;
const int N = 5005;int n, w[N], b[N], sw[N], sb[N], ans[N<<1];signed main()
{cin >> n;w[1] = 1, b[2] = 1, w[3] = 1, b[3] = 1;for(int i=4; i<=n; i++)w[i] = (w[i-1] + w[i-2]) % mod,b[i] = (b[i-1] + b[i-2]) % mod;for(int i=1; i<=n; i++)sb[i] = (sb[i-1] + b[i]) % mod,sw[i] = (sw[i-1] + w[i]) % mod;for(int i=1; i<=n; i++)ans[i] = sw[n-i] * w[i+1] % mod;for(int i=1; i<=n; i++)for(int j=1; j<=n; j++)ans[i+j] += (sb[n-max(i,j)] * w[i] % mod) * w[j+1] % mod, ans[i+j] %= mod;for(int i=1; i<=2*n; i++) cout << ans[i] << " ";
}
总结
预估 100 + 100 + 0 100+100+0 100+100+0,实际 90 + 100 + 0 90+100+0 90+100+0。场上三题大概都看了眼,发现 T2 比较简单,场上优先写了这题,比较自信,没有写拍。然后开 T1,T1 暴露了我数论接触不多的缺陷,先写了个暴力然后找规律推式子。推完了发现不会筛法求欧拉函数,也不知道一些高深的公式,就推了个奇奇怪怪的基于埃筛的 O ( n log log n ) O(\sqrt n \log \log \sqrt n) O(nloglogn) 方法。写完代码之后验了几个小数据没什么问题。T3 剩的时间不是很多,想的不是很全面,没有想到根据 lca 去讨论,写了个奇奇怪怪的平方 dp,由于时间不多且分讨巨多没有实现。
相关文章:

CYEZ 模拟赛 9
A a ⊥ b ⇒ a − b ⊥ a b (1) a \perp b \Rightarrow a-b \perp ab \tag {1} a⊥b⇒a−b⊥ab(1) 证明: gcd ( a , b ) gcd ( b , a − b ) \gcd(a,b) \gcd(b, a-b) gcd(a,b)gcd(b,a−b),故 a − b ⊥ b a - b \perp b a−b⊥b,同…...
typescript: Builder Pattern
/*** file: CarBuilderts.ts* TypeScript 实体类 Model* Builder Pattern* 生成器是一种创建型设计模式, 使你能够分步骤创建复杂对象。* https://stackoverflow.com/questions/12827266/get-and-set-in-typescript* https://github.com/Microsoft/TypeScript/wiki/…...
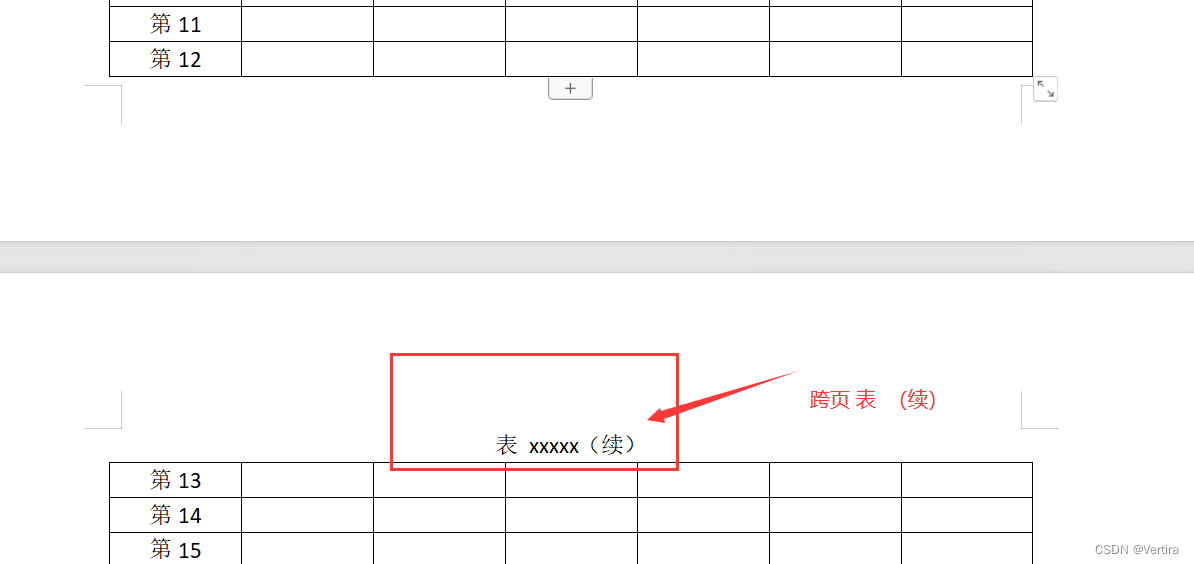
WPS/word 表格跨行如何续表、和表的名称
1:具体操作: 将光标定位在跨页部分的第一行任意位置,按下快捷键ctrlshiftenter,就可以在跨页的表格上方插入空行(在空行可以写,表1-3 xxxx(续)) 在空行中输入…...
Python的NumPy库(一)基础用法
NumPy库并不是Python的标准库,但其在机器学习、大数据等很多领域有非常广泛的应用,NumPy本身就有比较多的内容,全部的学习可能涉及许多的内容,但我们在这里仅学习常见的使用,这些内容对于我们日常使用NumPy是足够的。 …...
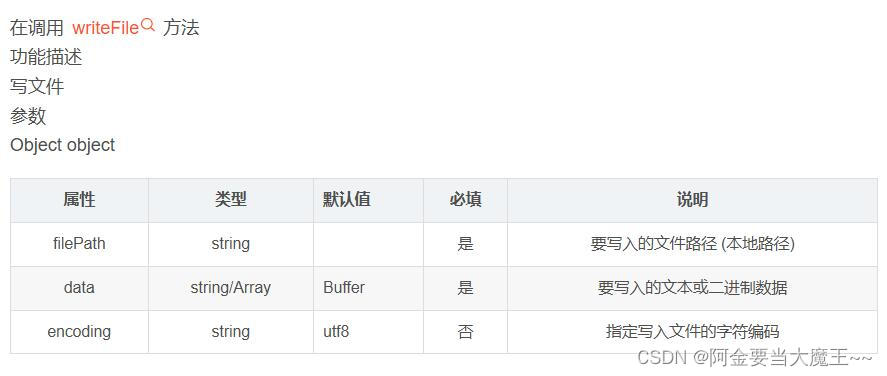
uniapp app 导出excel 表格
直接复制运行 <template><view><button click"tableToExcel">导出一个表来看</button><view>{{ successTip }}</view></view> </template><script>export default {data() {return {successTip: }},metho…...
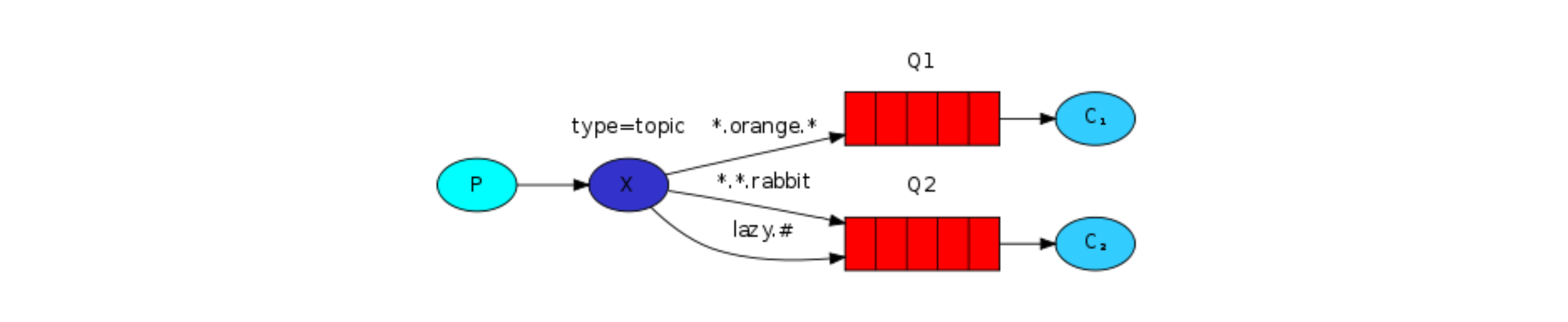
【RabbitMQ】常用消息模型详解
文章目录 AMQP协议的回顾RabbitMQ支持的消息模型第一种模型(直连)开发生产者开发消费者生产者、消费者开发优化API参数细节 第二种模型(work quene)开发生产者开发消费者消息自动确认机制 第三种模型(fanout)开发生产者开发消费者 第四种模型(Routing)开发生产者开发消费者 第五…...

图像拼接后丢失数据,转tiff报错rasterfile failed: an unknown
图像拼接后丢失数据 不仅是数据丢失了,还有个未知原因报错 部分数据存在值不存在的情况 原因 处理遥感数据很容易,磁盘爆满了 解决方案 清理一些无用数据,准备买个2T的外接硬盘用着了。 然后重新做处理...

Nginx之日志模块解读
目录 基本介绍 配置指令 access_log(访问日志) error_log( 错误日志) 基本介绍 Nginx日志主要分为两种:access_log(访问日志)和error_log(错误日志)。Nginx日志主要记录以下信息: 记录Nginx服务启动…...
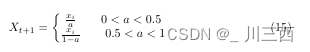
latex方程组编写,一种可以保证方程编号自适应的方法
问题描述: 在利用latex编写方程组时,可以有很多种方法,但不总是编辑好的公式能够显示出编号,故提出一种有效的方程组编写方法 方法: \begin{equation}X_{ t1}\left \{ \begin{matrix}\frac{x_{i}}{a} \quad\quad 0&l…...
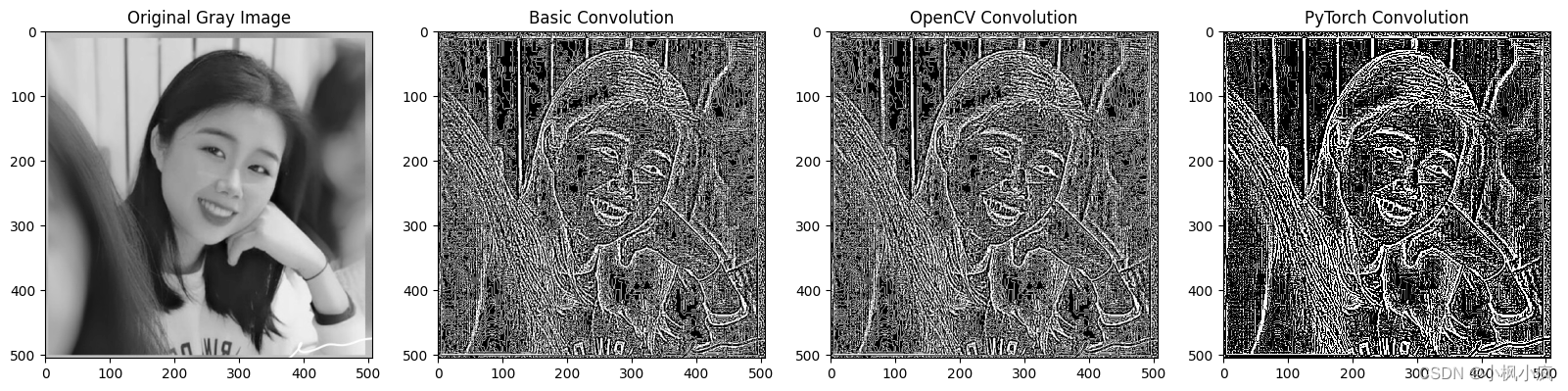
深度学习基础 2D卷积(1)
什么是2D卷积 2D参数量怎么计算 以pytorch为例子,2D卷积在设置的时候具有以下参数,具有输入通道的多少(这个决定了卷积核的通道数量),滤波器数量,这个是有多少个滤波器,越多提取的特征就越有用…...

OpenCV DNN C++ 使用 YOLO 模型推理
OpenCV DNN C 使用 YOLO 模型推理 引言 YOLO(You Only Look Once)是一种流行的目标检测算法,因其速度快和准确度高而被广泛应用。OpenCV 的 DNN(Deep Neural Networks)模块为我们提供了一个简单易用的 API࿰…...
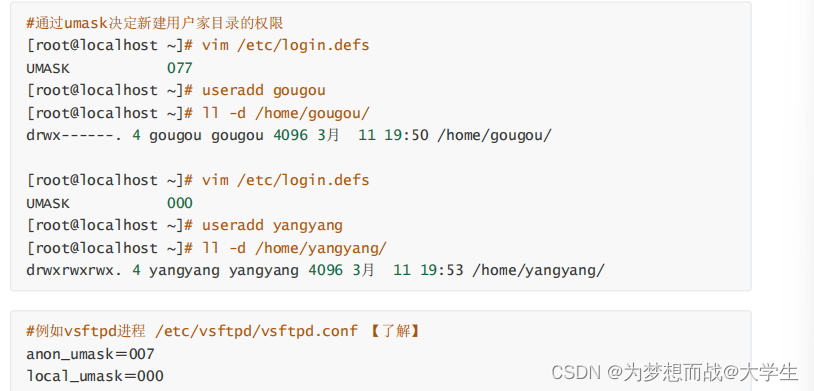
第八章 Linux文件系统权限
目录 8.1 文件的一般权限 1.修改文件或目录的权限---chmod命令 2.对于文件和目录,r,w,x有不同的作用: 3.修改文件或目录的所属主和组---chown,chgrp 8.2 文件和目录的特殊权限 三种通过字符描述文件权限 8.3 ACL 权限 1.A…...
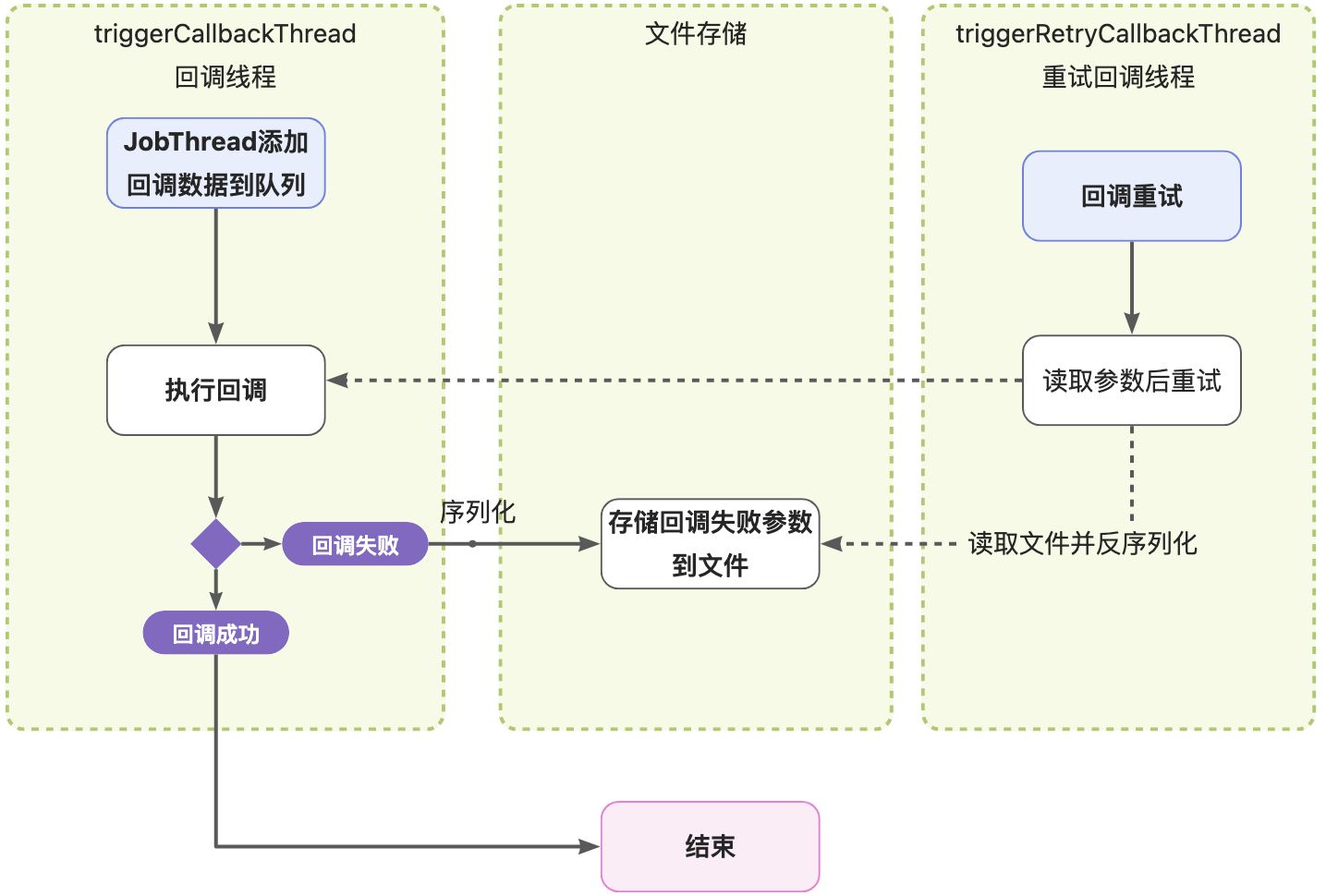
XXL-JOB源码梳理——一文理清XXL-JOB实现方案
分布式定时任务调度系统 流程分析 一个分布式定时任务,需要具备有以下几点功能: 核心功能:定时调度、任务管理、可观测日志高可用:集群、分片、失败处理高性能:分布式锁扩展功能:可视化运维、多语言、任…...
java做个qq机器人
前置的条件 机器人是基于mirai框架实现的。根据官方的文档,建议使用openjdk11。 我这里使用的编辑工具是idea2023 在idea中新建一个maven项目,虽然可以使用gradle进行构建,不过我这里由于网络问题没有跑通。 pom.xml <dependency>&l…...

前端 | AjaxAxios模块
文章目录 1. Ajax1.1 Ajax介绍1.2 Ajax作用1.3 同步异步1.4 原生Ajax 2. Axios2.1 Axios下载2.2 Axios基本使用2.3 Axios方法 1. Ajax 1.1 Ajax介绍 Ajax: 全称(Asynchronous JavaScript And XML),异步的JavaScript和XML。 1.2 Ajax作用 …...

高效的ProtoBuf
一、背景 Google ProtoBuf介绍 这篇文章我们讲了怎么使用ProtoBuf进行序列化,但ProtoBuf怎么做到最高效的,它的数据又是如何压缩的,下面先看一个例子,然后再讲ProtoBuf压缩机制。 二、案例 网上有各种序列化方式性能对比&#…...

删除SQL记录
删除记录的方式汇总: 根据条件删除:DELETE FROM tb_name [WHERE options] [ [ ORDER BY fields ] LIMIT n ] 全部删除(表清空,包含自增计数器重置):TRUNCATE tb_namedelete和truncate的区别: d…...

数据结构--》探索数据结构中的字符串结构与算法
本文将带你深入了解串的基本概念、表示方法以及串操作的常见算法。通过深入理解串的相关概念和操作,我们将能够更好地应用它们来解决算法问题。 无论你是初学者还是进阶者,本文将为你提供简单易懂、实用可行的知识点,帮助你更好地掌握串在数据…...
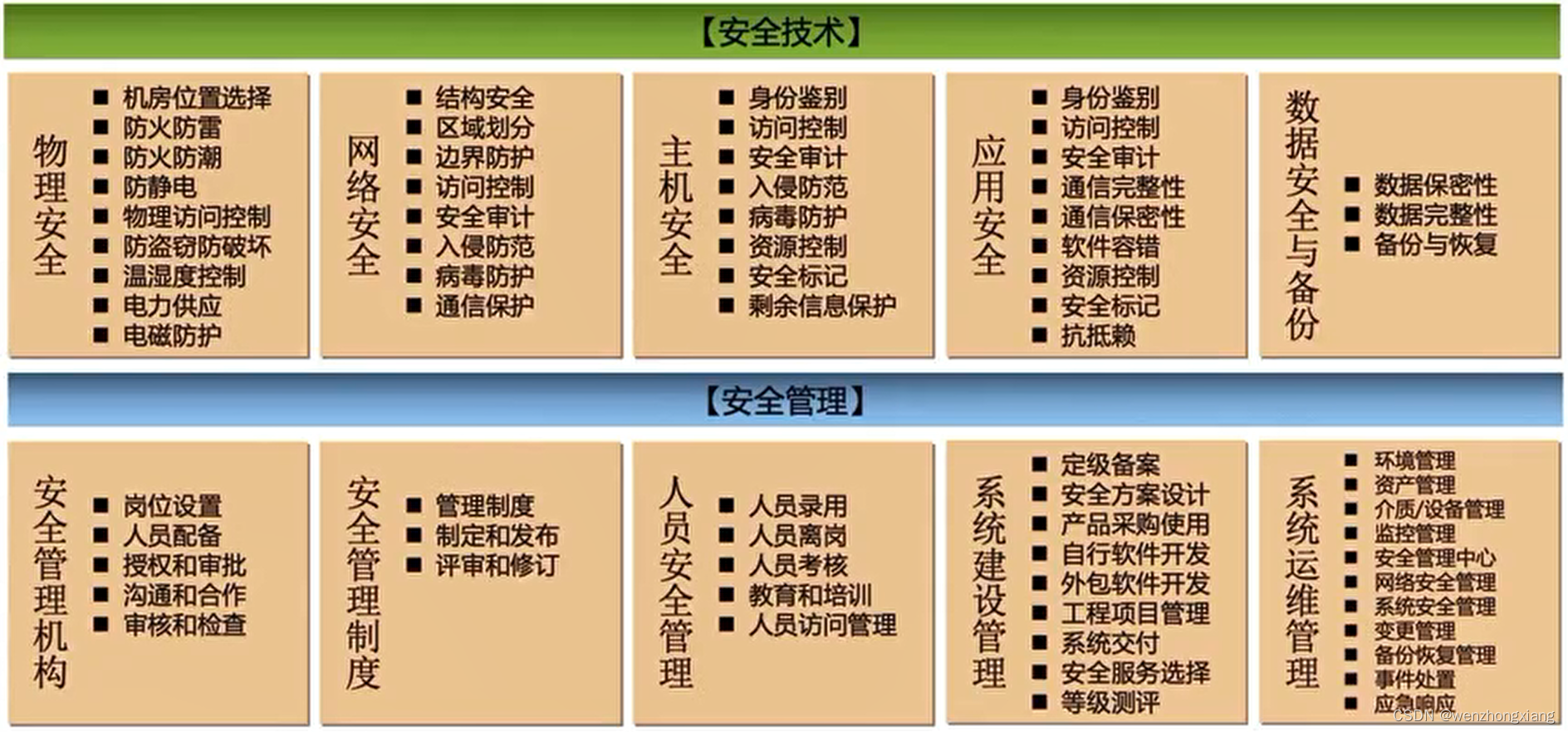
云安全之等级保护详解
等级保护概念 网络安全等级保护,是对信息系统分等级实行安全保护,对信息系统中使用的安全产品实行按等级管理,对信息系统中发生的信息安全事件分等级进行响应、处置。 网络安全等级保护的核心内容是:国家制定统一的政策、标准&a…...

VUE状态持久化,储存动态路由
1. vuex persistPlugin.js 文件 const routerKey "ROUTER_KEY";export default (store) > {// 刷新页面时,存储改变的数据window.addEventListener("beforeunload", () > {localStorage.setItem(routerKey, JSON.stringify(store.stat…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

uniapp 开发ios, xcode 提交app store connect 和 testflight内测
uniapp 中配置 配置manifest 文档:manifest.json 应用配置 | uni-app官网 hbuilderx中本地打包 下载IOS最新SDK 开发环境 | uni小程序SDK hbulderx 版本号:4.66 对应的sdk版本 4.66 两者必须一致 本地打包的资源导入到SDK 导入资源 | uni小程序SDK …...

raid存储技术
1. 存储技术概念 数据存储架构是对数据存储方式、存储设备及相关组件的组织和规划,涵盖存储系统的布局、数据存储策略等,它明确数据如何存储、管理与访问,为数据的安全、高效使用提供支撑。 由计算机中一组存储设备、控制部件和管理信息调度的…...

当下AI智能硬件方案浅谈
背景: 现在大模型出来以后,打破了常规的机械式的对话,人机对话变得更聪明一点。 对话用到的技术主要是实时音视频,简称为RTC。下游硬件厂商一般都不会去自己开发音视频技术,开发自己的大模型。商用方案多见为字节、百…...

比特币:固若金汤的数字堡垒与它的四道防线
第一道防线:机密信函——无法破解的哈希加密 将每一笔比特币交易比作一封在堡垒内部传递的机密信函。 解释“哈希”(Hashing)就是一种军事级的加密术(SHA-256),能将信函内容(交易细节…...

【大厂机试题解法笔记】矩阵匹配
题目 从一个 N * M(N ≤ M)的矩阵中选出 N 个数,任意两个数字不能在同一行或同一列,求选出来的 N 个数中第 K 大的数字的最小值是多少。 输入描述 输入矩阵要求:1 ≤ K ≤ N ≤ M ≤ 150 输入格式 N M K N*M矩阵 输…...
:PyQuery 框架)
Python爬虫(四):PyQuery 框架
PyQuery 框架详解与对比 BeautifulSoup 第一部分:PyQuery 框架介绍 1. PyQuery 是什么? PyQuery 是一个 Python 的 HTML/XML 解析库,它采用了 jQuery 的语法风格,让开发者能够用类似前端 jQuery 的方式处理文档解析。它的核心特…...

中国政务数据安全建设细化及市场需求分析
(基于新《政务数据共享条例》及相关法规) 一、引言 近年来,中国政府高度重视数字政府建设和数据要素市场化配置改革。《政务数据共享条例》(以下简称“《共享条例》”)的发布,与《中华人民共和国数据安全法》(以下简称“《数据安全法》”)、《中华人民共和国个人信息…...
