算法-排序算法
0、算法概述
0.1 算法分类
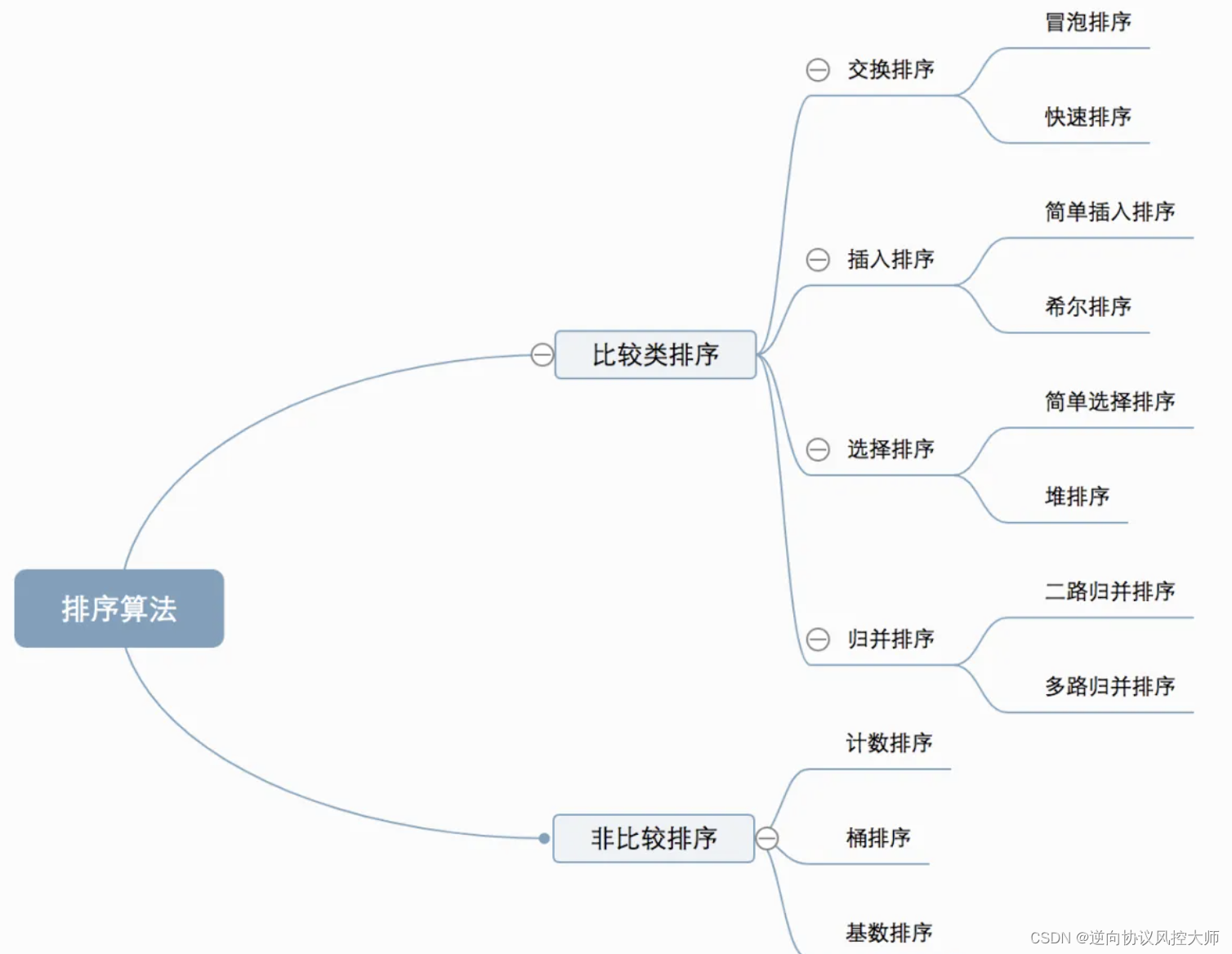
十种常见排序算法可以分为两大类:
比较类排序:通过比较来决定元素间的相对次序,由于其时间复杂度不能突破O(nlogn),因此也称为非线性时间比较类排序。
非比较类排序:不通过比较来决定元素间的相对次序,它可以突破基于比较排序的时间下界,以线性时间运行,因此也称为线性时间非比较类排序。
0.2 算法复杂度
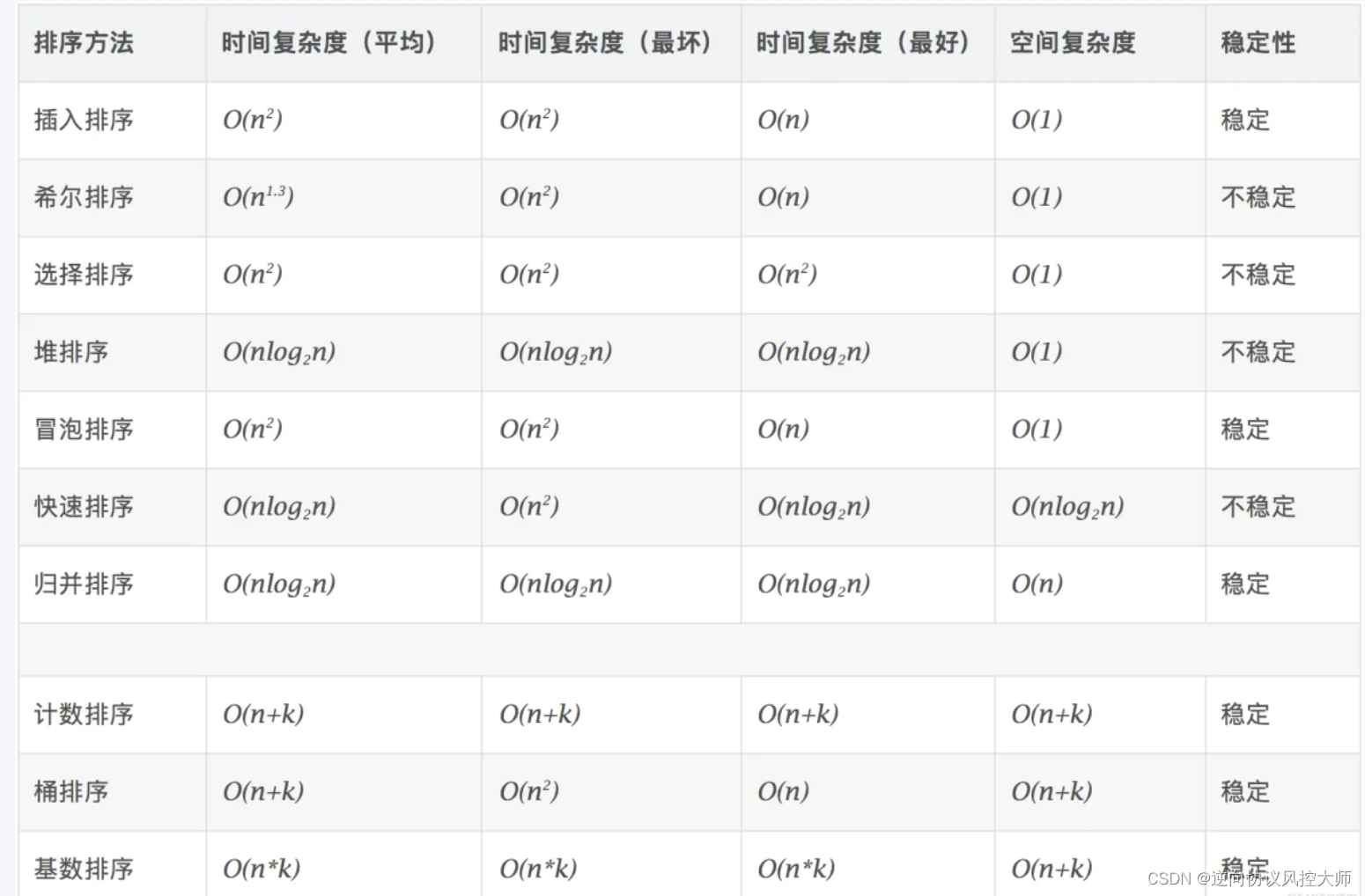
0.3 相关概念
稳定:如果a原本在b前面,而a=b,排序之后a仍然在b的前面。
不稳定:如果a原本在b的前面,而a=b,排序之后 a 可能会出现在 b 的后面。
时间复杂度:对排序数据的总的操作次数。反映当n变化时,操作次数呈现什么规律。
空间复杂度:是指算法在计算机
内执行时所需存储空间的度量,它也是数据规模n的函数。
1、冒泡排序(Bubble Sort)
冒泡排序是一种简单的排序算法。它重复地走访过要排序的数列,一次比较两个元素,如果它们的顺序错误就把它们交换过来。走访数列的工作是重复地进行直到没有再需要交换,也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。
1.1 算法描述
比较相邻的元素。如果第一个比第二个大,就交换它们两个;
对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对,这样在最后的元素应该会是最大的数;
针对所有的元素重复以上的步骤,除了最后一个;
重复步骤1~3,直到排序完成。
1.2 动图演示
1.3 代码实现
function bubbleSort(arr) {
var len = arr.length;
for (var i = 0; i < len - 1; i++) {
for (var j = 0; j < len - 1 - i; j++) {
if (arr[j] > arr[j+1]) { // 相邻元素两两对比
var temp = arr[j+1]; // 元素交换
arr[j+1] = arr[j];
arr[j] = temp;
}
}
}
return arr;
}
2、选择排序(Selection Sort)
选择排序(Selection-sort)是一种简单直观的排序算法。它的工作原理:首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置,然后,再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。以此类推,直到所有元素均排序完毕。
2.1 算法描述
n个记录的直接选择排序可经过n-1趟直接选择排序得到有序结果。具体算法描述如下:
初始状态:无序区为R[1..n],有序区为空;
第i趟排序(i=1,2,3…n-1)开始时,当前有序区和无序区分别为R[1..i-1]和R(i..n)。该趟排序从当前无序区中-选出关键字最小的记录 R[k],将它与无序区的第1个记录R交换,使R[1..i]和R[i+1..n)分别变为记录个数增加1个的新有序区和记录个数减少1个的新无序区;
n-1趟结束,数组有序化了。
2.2 动图演示
2.3 代码实现
function selectionSort(arr) {
var len = arr.length;
var minIndex, temp;
for (var i = 0; i < len - 1; i++) {
minIndex = i;
for (var j = i + 1; j < len; j++) {
if (arr[j] < arr[minIndex]) { // 寻找最小的数
minIndex = j; // 将最小数的索引保存
}
}
temp = arr[i];
arr[i] = arr[minIndex];
arr[minIndex] = temp;
}
return arr;
}
2.4 算法分析
表现最稳定的排序算法之一,因为无论什么数据进去都是O(n2)的时间复杂度,所以用到它的时候,数据规模越小越好。唯一的好处可能就是不占用额外的内存空间了吧。理论上讲,选择排序可能也是平时排序一般人想到的最多的排序方法了吧。
3、插入排序(Insertion Sort)
插入排序(Insertion-Sort)的算法描述是一种简单直观的排序算法。它的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。
3.1 算法描述
一般来说,插入排序都采用in-place在数组上实现。具体算法描述如下:
从第一个元素开始,该元素可以认为已经被排序;
取出下一个元素,在已经排序的元素序列中从后向前扫描;
如果该元素(已排序)大于新元素,将该元素移到下一位置;
重复步骤3,直到找到已排序的元素小于或者等于新元素的位置;
将新元素插入到该位置后;
重复步骤2~5。
3.2 动图演示
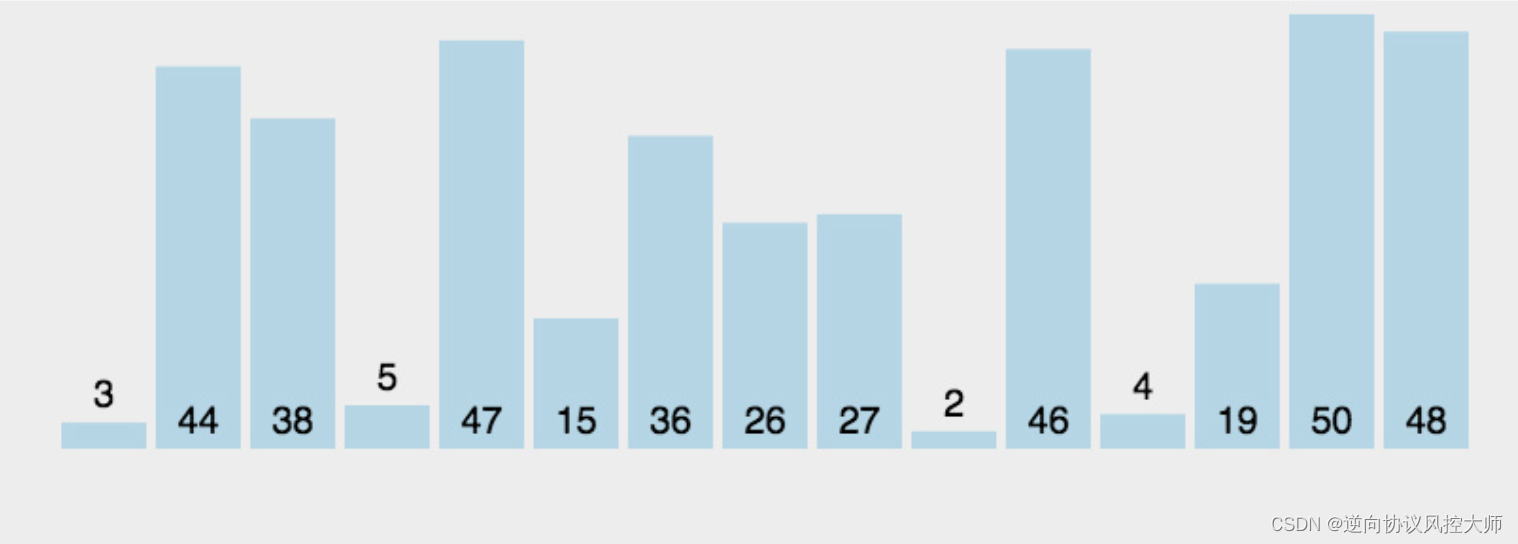
3.2 代码实现
function insertionSort(arr) {
var len = arr.length;
var preIndex, current;
for (var i = 1; i < len; i++) {
preIndex = i - 1;
current = arr[i];
while (preIndex >= 0 && arr[preIndex] > current) {
arr[preIndex + 1] = arr[preIndex];
preIndex--;
}
arr[preIndex + 1] = current;
}
return arr;
}
3.4 算法分析
插入排序在实现上,通常采用in-place排序(即只需用到O(1)的额外空间的排序),因而在从后向前扫描过程中,需要反复把已排序元素逐步向后挪位,为最新元素提供插入空间。
4、希尔排序(Shell Sort)
1959年Shell发明,第一个突破O(n2)的排序算法,是简单插入排序的改进版。它与插入排序的不同之处在于,它会优先比较距离较远的元素。希尔排序又叫缩小增量排序。
4.1 算法描述
先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序,具体算法描述:
选择一个增量序列t1,t2,…,tk,其中ti>tj,tk=1;
按增量序列个数k,对序列进行k 趟排序;
每趟排序,根据对应的增量ti,将待排序列分割成若干长度为m 的子序列,分别对各子表进行直接插入排序。仅增量因子为1 时,整个序列作为一个表来处理,表长度即为整个序列的长度。
4.2 动图演示
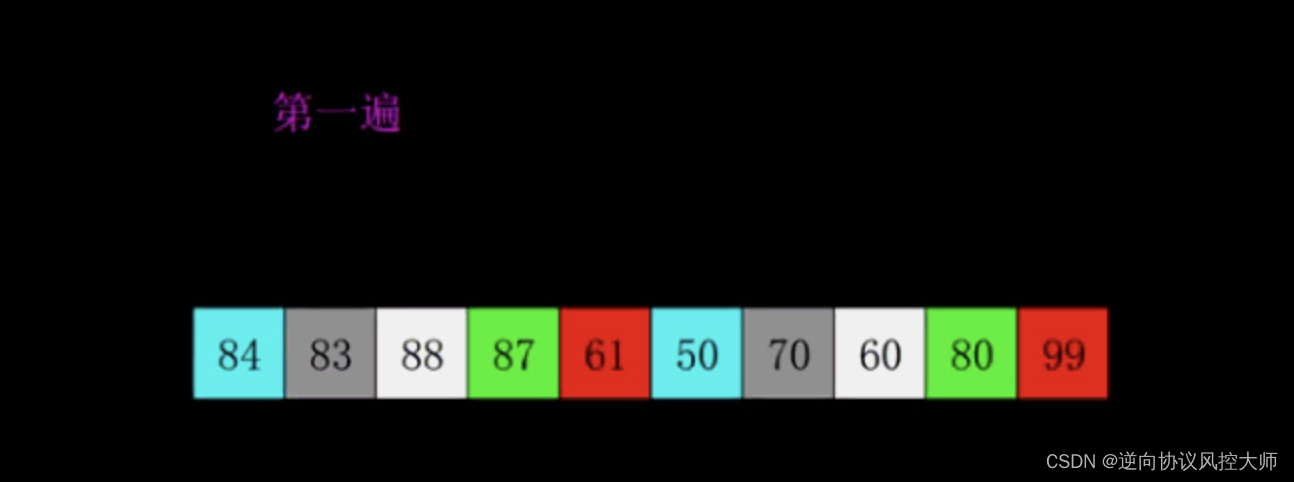
4.3 代码实现
// 修改于 2019-03-06
function shellSort(arr) {
var len = arr.length;
for (var gap = Math.floor(len / 2); gap > 0; gap = Math.floor(gap / 2)) {
// 注意:这里和动图演示的不一样,动图是分组执行,实际操作是多个分组交替执行
for (var i = gap; i < len; i++) {
var j = i;
var current = arr[i];
while (j - gap >= 0 && current < arr[j - gap]) {
arr[j] = arr[j - gap];
j = j - gap;
}
arr[j] = current;
}
}
return arr;
}
4.4 算法分析
希尔排序的核心在于间隔序列的设定。既可以提前设定好间隔序列,也可以动态的定义间隔序列。动态定义间隔序列的算法是《算法(第4版)》的合著者Robert Sedgewick提出的。
5、归并排序(Merge Sort)
归并排序是建立在归并操作上的一种有效的排序算法。该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为2-路归并。
5.1 算法描述
把长度为n的输入序列分成两个长度为n/2的子序列;
对这两个子序列分别采用归并排序;
将两个排序好的子序列合并成一个最终的排序序列。
5.2 动图演示
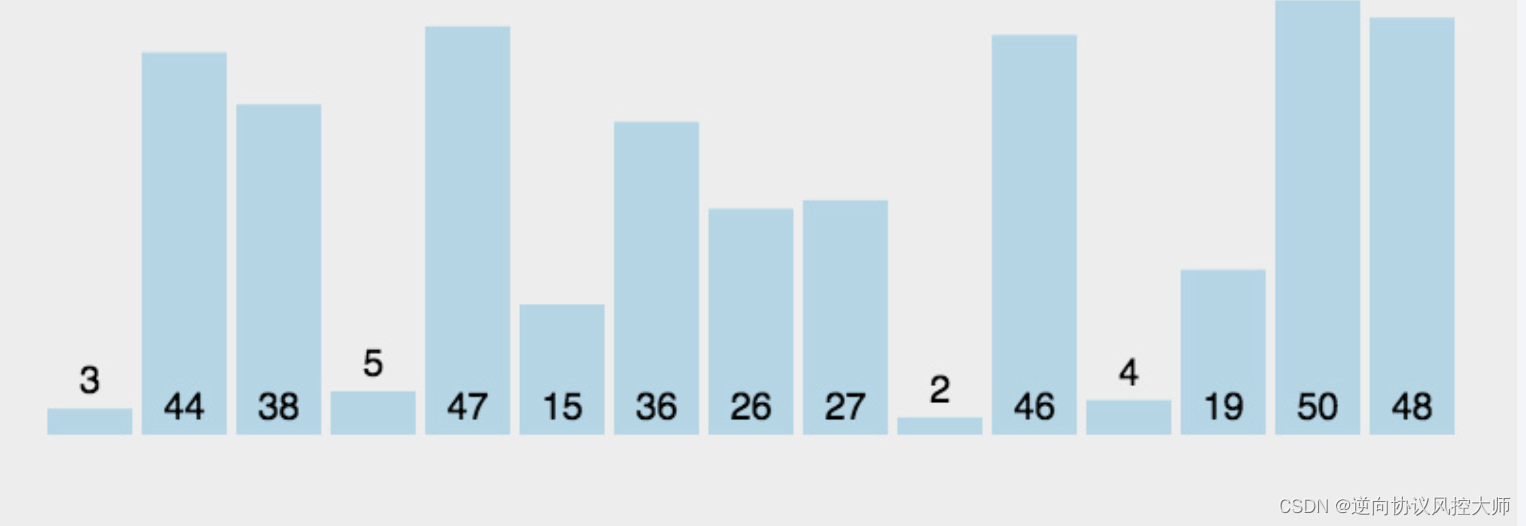
5.3 代码实现
function mergeSort(arr) {
var len = arr.length;
if (len < 2) {
return arr;
}
var middle = Math.floor(len / 2),
left = arr.slice(0, middle),
right = arr.slice(middle);
return merge(mergeSort(left), mergeSort(right));
}
function merge(left, right) {
var result = [];
while (left.length>0 && right.length>0) {
if (left[0] <= right[0]) {
result.push(left.shift());
}else {
result.push(right.shift());
}
}
while (left.length)
result.push(left.shift());
while (right.length)
result.push(right.shift());
return result;
}
5.4 算法分析
归并排序是一种稳定的排序方法。和选择排序一样,归并排序的性能不受输入数据的影响,但表现比选择排序好的多,因为始终都是O(nlogn)的时间复杂度。代价是需要额外的内存空间。
6、快速排序(Quick Sort)
快速排序的基本思想:通过一趟排序将待排记录分隔成独立的两部分,其中一部分记录的关键字均比另一部分的关键字小,则可分别对这两部分记录继续进行排序,以达到整个序列有序。
6.1 算法描述
快速排序使用分治法来把一个串(list)分为两个子串(sub-lists)。具体算法描述如下:
从数列中挑出一个元素,称为 “基准”(pivot);
重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任一边)。在这个分区退出之后,该基准就处于数列的中间位置。这个称为分区(partition)操作;
递归地(recursive)把小于基准值元素的子数列和大于基准值元素的子数列排序。
6.2 动图演示
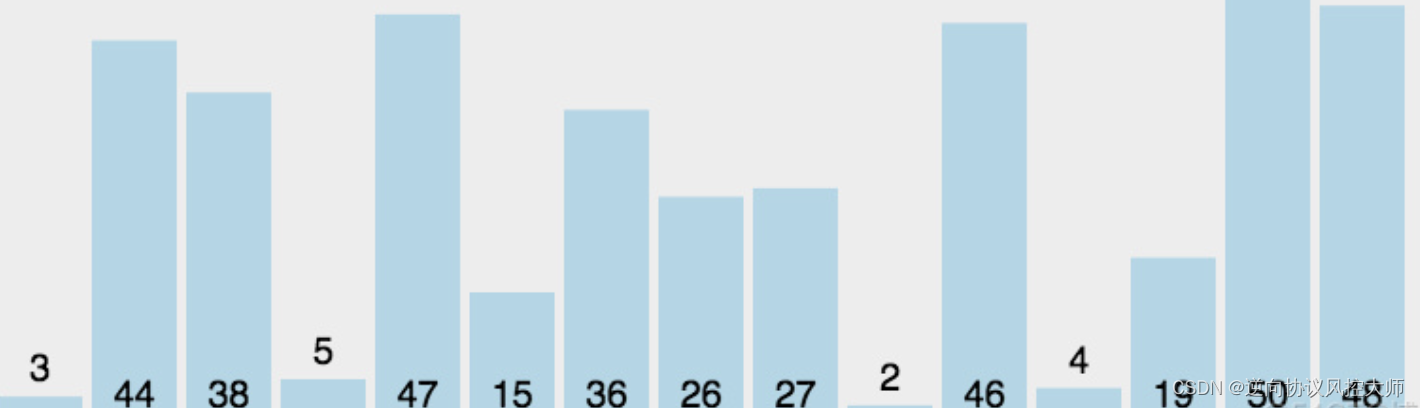
6.3 代码实现
function quickSort(arr, left, right) {
var len = arr.length,
partitionIndex,
left =typeof left !='number' ? 0 : left,
right =typeof right !='number' ? len - 1 : right;
if (left < right) {
partitionIndex = partition(arr, left, right);
quickSort(arr, left, partitionIndex-1);
quickSort(arr, partitionIndex+1, right);
}
return arr;
}
function partition(arr, left ,right) { // 分区操作
var pivot = left, // 设定基准值(pivot)
index = pivot + 1;
for (var i = index; i <= right; i++) {
if (arr[i] < arr[pivot]) {
swap(arr, i, index);
index++;
}
}
swap(arr, pivot, index - 1);
return index-1;
}
function swap(arr, i, j) {
var temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
7、堆排序(Heap Sort)
堆排序(Heapsort)是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构,并同时满足堆积的性质:即子结点的键值或索引总是小于(或者大于)它的父节点。
7.1 算法描述
将初始待排序关键字序列(R1,R2….Rn)构建成大顶堆,此堆为初始的无序区;
将堆顶元素R[1]与最后一个元素R[n]交换,此时得到新的无序区(R1,R2,……Rn-1)和新的有序区(Rn),且满足R[1,2…n-1]<=R[n];
由于交换后新的堆顶R[1]可能违反堆的性质,因此需要对当前无序区(R1,R2,……Rn-1)调整为新堆,然后再次将R[1]与无序区最后一个元素交换,得到新的无序区(R1,R2….Rn-2)和新的有序区(Rn-1,Rn)。不断重复此过程直到有序区的元素个数为n-1,则整个排序过程完成。
7.2 动图演示
7.3 代码实现
var len; // 因为声明的多个函数都需要数据长度,所以把len设置成为全局变量
function buildMaxHeap(arr) { // 建立大顶堆
len = arr.length;
for (var i = Math.floor(len/2); i >= 0; i--) {
heapify(arr, i);
}
}
function heapify(arr, i) { // 堆调整
var left = 2 * i + 1,
right = 2 * i + 2,
largest = i;
if (left < len && arr[left] > arr[largest]) {
largest = left;
}
if (right < len && arr[right] > arr[largest]) {
largest = right;
}
if (largest != i) {
swap(arr, i, largest);
heapify(arr, largest);
}
}
function swap(arr, i, j) {
var temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
function heapSort(arr) {
buildMaxHeap(arr);
for (var i = arr.length - 1; i > 0; i--) {
swap(arr, 0, i);
len--;
heapify(arr, 0);
}
return arr;
}
8、计数排序(Counting Sort)
计数排序不是基于比较的排序算法,其核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。 作为一种线性时间复杂度的排序,计数排序要求输入的数据必须是有确定范围的整数。
8.1 算法描述
找出待排序的数组中最大和最小的元素;
统计数组中每个值为i的元素出现的次数,存入数组C的第i项;
对所有的计数累加(从C中的第一个元素开始,每一项和前一项相加);
反向填充目标数组:将每个元素i放在新数组的第C(i)项,每放一个元素就将C(i)减去1。
8.2 动图演示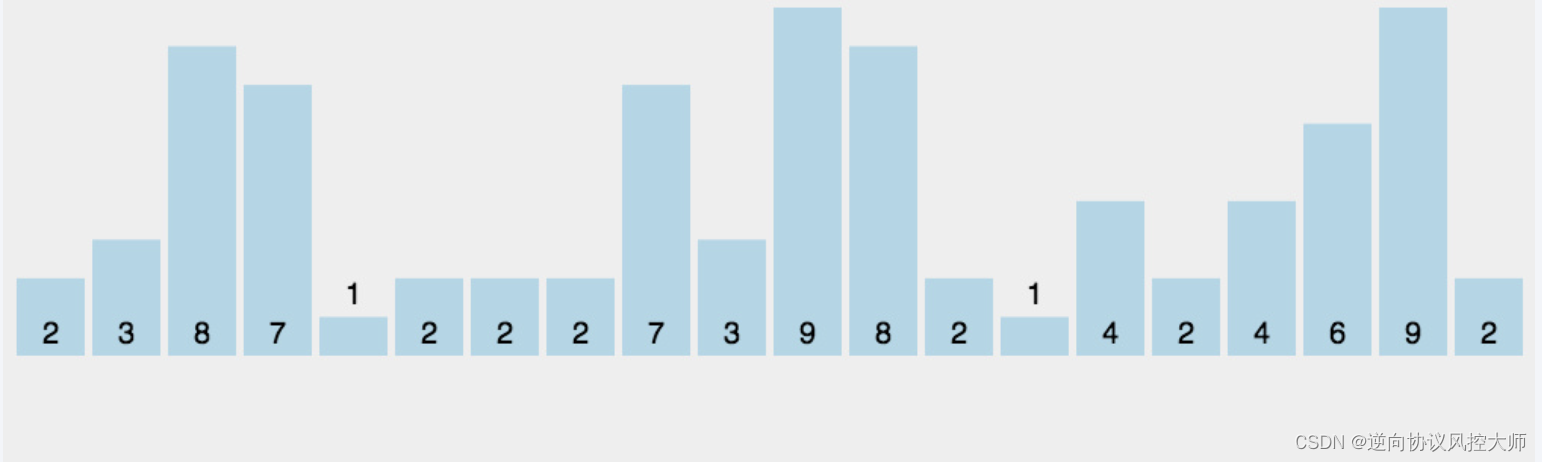
8.3 代码实现
function countingSort(arr, maxValue) {
var bucket =new Array(maxValue + 1),
sortedIndex = 0;
arrLen = arr.length,
bucketLen = maxValue + 1;
for (var i = 0; i < arrLen; i++) {
if (!bucket[arr[i]]) {
bucket[arr[i]] = 0;
}
bucket[arr[i]]++;
}
for (var j = 0; j < bucketLen; j++) {
while(bucket[j] > 0) {
arr[sortedIndex++] = j;
bucket[j]--;
}
}
return arr;
}
8.4 算法分析
计数排序是一个稳定的排序算法。当输入的元素是 n 个 0到 k 之间的整数时,时间复杂度是O(n+k),空间复杂度也是O(n+k),其排序速度快于任何比较排序算法。当k不是很大并且序列比较集中时,计数排序是一个很有效的排序算法。
9、桶排序(Bucket Sort)
桶排序是计数排序的升级版。它利用了函数的映射关系,高效与否的关键就在于这个映射函数的确定。桶排序 (Bucket sort)的工作的原理:假设输入数据服从均匀分布,将数据分到有限数量的桶里,每个桶再分别排序(有可能再使用别的排序算法或是以递归方式继续使用桶排序进行排)。
9.1 算法描述
设置一个定量的数组当作空桶;
遍历输入数据,并且把数据一个一个放到对应的桶里去;
对每个不是空的桶进行排序;
从不是空的桶里把排好序的数据拼接起来。
9.2 图片演示
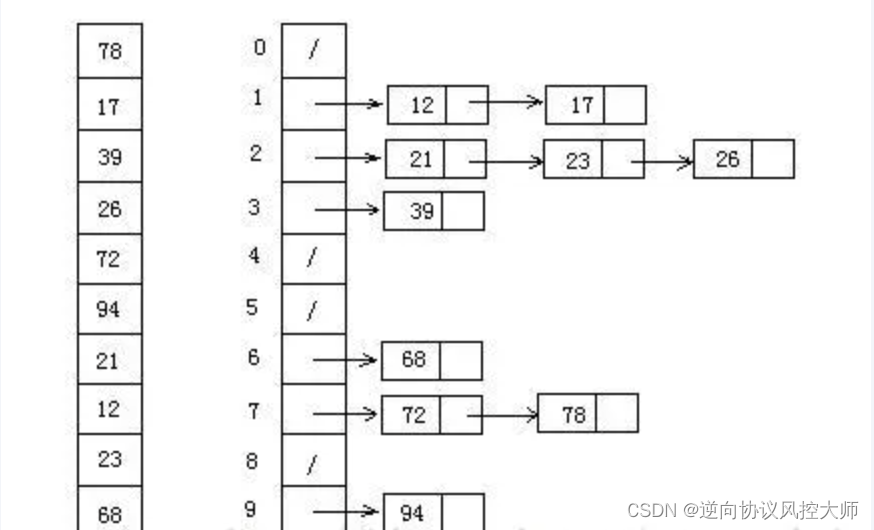
9.3 代码实现
function bucketSort(arr, bucketSize) {
if (arr.length === 0) {
return arr;
}
var i;
var minValue = arr[0];
var maxValue = arr[0];
for (i = 1; i < arr.length; i++) {
if (arr[i] < minValue) {
minValue = arr[i]; // 输入数据的最小值
}else if (arr[i] > maxValue) {
maxValue = arr[i]; // 输入数据的最大值
}
}
// 桶的初始化
var DEFAULT_BUCKET_SIZE = 5; // 设置桶的默认数量为5
bucketSize = bucketSize || DEFAULT_BUCKET_SIZE;
var bucketCount = Math.floor((maxValue - minValue) / bucketSize) + 1;
var buckets =new Array(bucketCount);
for (i = 0; i < buckets.length; i++) {
buckets[i] = [];
}
// 利用映射函数将数据分配到各个桶中
for (i = 0; i < arr.length; i++) {
buckets[Math.floor((arr[i] - minValue) / bucketSize)].push(arr[i]);
}
arr.length = 0;
for (i = 0; i < buckets.length; i++) {
insertionSort(buckets[i]); // 对每个桶进行排序,这里使用了插入排序
for (var j = 0; j < buckets[i].length; j++) {
arr.push(buckets[i][j]);
}
}
return arr;
}
9.4 算法分析
桶排序最好情况下使用线性时间O(n),桶排序的时间复杂度,取决与对各个桶之间数据进行排序的时间复杂度,因为其它部分的时间复杂度都为O(n)。很显然,桶划分的越小,各个桶之间的数据越少,排序所用的时间也会越少。但相应的空间消耗就会增大。
10、基数排序(Radix Sort)
基数排序是按照低位先排序,然后收集;再按照高位排序,然后再收集;依次类推,直到最高位。有时候有些属性是有优先级顺序的,先按低优先级排序,再按高优先级排序。最后的次序就是高优先级高的在前,高优先级相同的低优先级高的在前。
10.1 算法描述
取得数组中的最大数,并取得位数;
arr为原始数组,从最低位开始取每个位组成radix数组;
对radix进行计数排序(利用计数排序适用于小范围数的特点);
10.2 动图演示
10.3 代码实现
var counter = [];
function radixSort(arr, maxDigit) {
var mod = 10;
var dev = 1;
for (var i = 0; i < maxDigit; i++, dev *= 10, mod *= 10) {
for(var j = 0; j < arr.length; j++) {
var bucket = parseInt((arr[j] % mod) / dev);
if(counter[bucket]==null) {
counter[bucket] = [];
}
counter[bucket].push(arr[j]);
}
var pos = 0;
for(var j = 0; j < counter.length; j++) {
var value =null;
if(counter[j]!=null) {
while ((value = counter[j].shift()) !=null) {
arr[pos++] = value;
}
}
}
}
return arr;
}
10.4 算法分析
基数排序基于分别排序,分别收集,所以是稳定的。但基数排序的性能比桶排序要略差,每一次关键字的桶分配都需要O(n)的时间复杂度,而且分配之后得到新的关键字序列又需要O(n)的时间复杂度。假如待排数据可以分为d个关键字,则基数排序的时间复杂度将是O(d*2n) ,当然d要远远小于n,因此基本上还是线性级别的。
基数排序的空间复杂度为O(n+k),其中k为桶的数量。一般来说n>>k,因此额外空间需要大概n个左右。
相关文章:

算法-排序算法
0、算法概述 0.1 算法分类 十种常见排序算法可以分为两大类: 比较类排序:通过比较来决定元素间的相对次序,由于其时间复杂度不能突破O(nlogn),因此也称为非线性时间比较类排序。 非比较类排序:不通过比较来决定元素间…...

Android_Monkey_测试执行策略及标准
一、Monkey命令概述 NO命令说明用法解释1 -p ALLOWED_PACKAGE用于指定某个apk,可以使用多个-p选项,但是每个-p命令选项只能用于一个apk 如果不指定-p,Monkey就会默认进行全系统测试。 -p com.android.contacts可以进行特定apk的Monkey测试2 …...
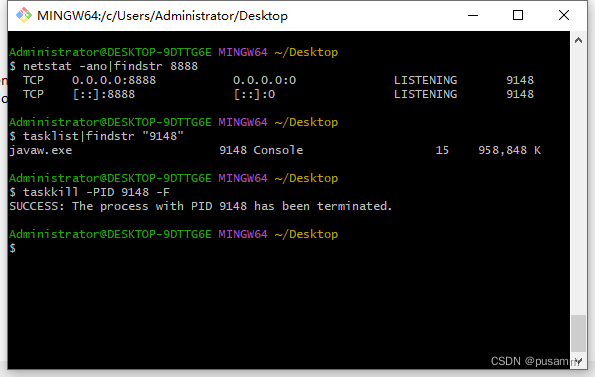
windows安装nginx
官网提供的下载地址:nginx: download nginx1.25.2下载地址:http://nginx.org/download/nginx-1.25.2.zip 直接运行nginx.exe会闪退,我们还得使用cmd/git bash/power shell 命令进行启动; 个人更喜欢git bash; 运行命…...

Java日期的学习篇
关于日期的学习 目录 关于日期的学习JDK8以前的APIDate Date常用APIDate的API应用 SimpleDateFormatSimpleDateFormat常用API测试 反向格式化(逆操作)测试 训练案例需求(秒杀活动)实现 Calendar需求痛点常见API应用测试 JDK8及以后的API(修改与新增)为啥学习(推荐使用)新增的AP…...

spark on hive
需要提前搭建好hive,并对hive进行配置。 1、将hive的配置文件添加到spark的目录下 cp $HIVE_HOME/conf/hive-site.xml $SPARK_HOME/conf2、开启hive的hivemetastore服务 提前创建好启动日志存放路径 mkdir $HIVE_HOME/logStart nohup /usr/local/lib/apache-hi…...

Linux Vi编辑器基础操作指南
Linux Vi编辑器基础操作指南 Linux中的Vi是一个强大的文本编辑器,虽然它有一些陡峭的学习曲线,但一旦掌握了基本操作,它就变得非常高效。以下是Vi编辑器的一些基本用法: 打开Vi编辑器: vi 文件名退出Vi编辑器ÿ…...
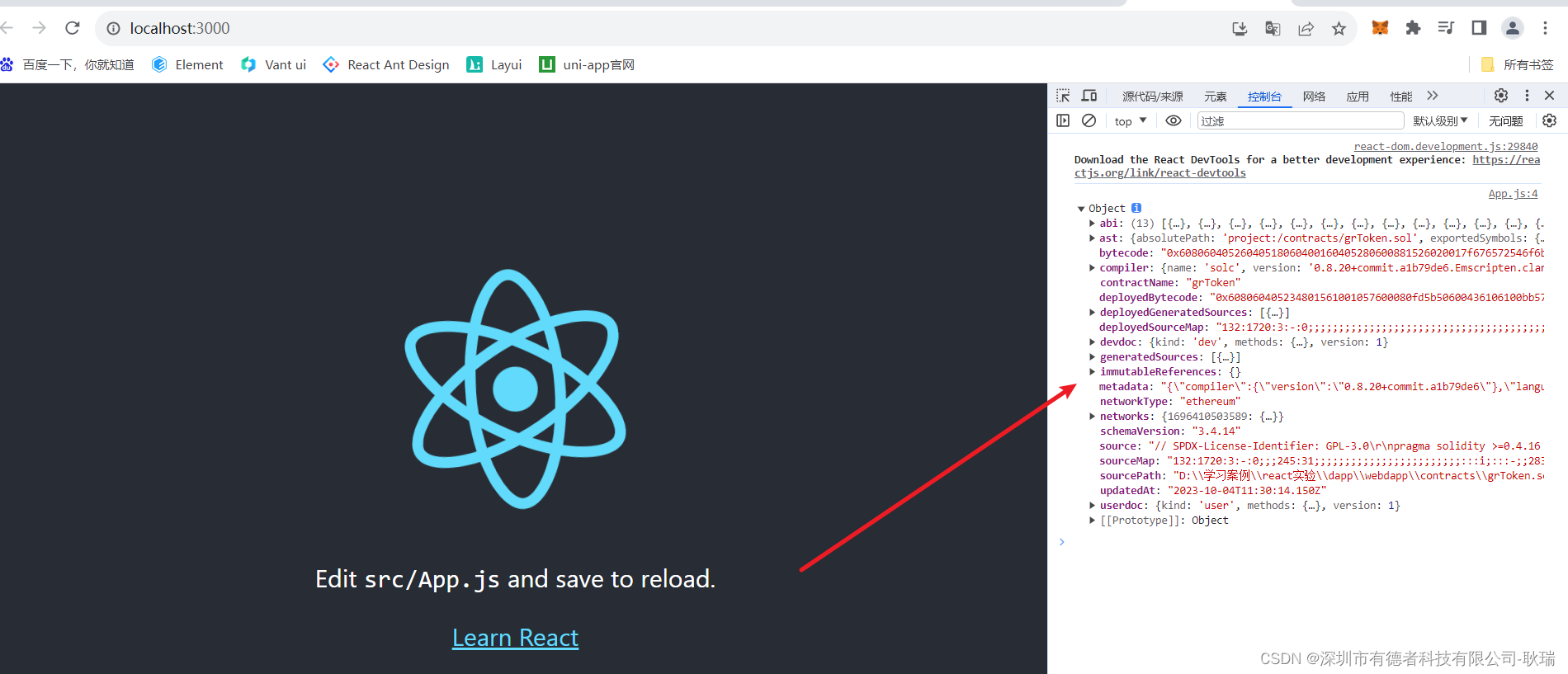
WEB3 创建React前端Dapp环境并整合solidity项目,融合项目结构便捷前端拿取合约 Abi
好 各位 经过我们上文 WEB3 solidity 带着大家编写测试代码 操作订单 创建/取消/填充操作 我们自己写了一个测试订单业务的脚本 没想到运行的还挺好的 那么 今天开始 我们就可以开始操作我们前端 Dapp 的一个操作了 在整个过程中 确实是没有我们后端的操作 或者说 我们自己就…...

rust运算
不同类型不能放在一起运算。如果非要计算,必须先强转成一个类型再运算。 一 、数字运算 (一)算术运算 a 10且b 5 名称运算符范例加ab的结果为15减-a-b的结果为5乘*a*b的结果为50除/a / b的结果为2求余%a % b的结果为0 Rust语言不支持自增…...

游戏引擎,脚本管理模块
编辑器中删除脚本,然后立即恢复删除的脚本关系正常编辑器中删除脚本,关掉编辑器,然后只恢复脚本,不恢复meta,然后再打开编辑器关系丢失编辑器中删除脚本,关掉编辑器,然后恢复脚本且恢复meta,然后再打开编辑…...

2023年7月工作经历三
年龄危机 传言:程序员干不过37岁,架构师干不过45岁,总监干不过55岁。我已经43岁了。当总监需要机遇;首下犯错,会扣领导工资;有的公司总监还需要出资。为了方便以后当总监,我还在超音速带过小团…...

1801_codesys产品主样本了解
全部学习汇总: GreyZhang/g_codesys: some codesys learning notes (github.com) 有些技术、学术的成长,氛围也是很重要的。我觉得工业控制,德国做得算是世界上很突出的。而这个巴伐利亚,更是突出中的佼佼者了。从这里的介绍看&am…...

flink的计时器
背景 在flink中,我们经常使用ontimer计时器实现很多逻辑的功能,常见的比如某个传感器温度增加连续超过1分钟的告警输出等,本文就来简单记录下计时器的作用 计时器 ontimer的定义 public void onTimer(long timestamp, OnTimerContext ctx…...
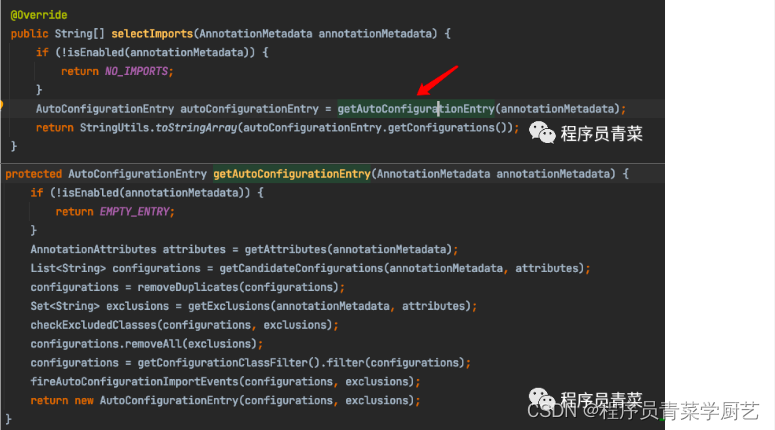
@SpringBootApplication剖析
一、前言 在SpringBoot项目中启动类必须加一个注解SpringBootApplication,今天我们来剖析SpringBootApplication这个注解到底做了些什么。 二、SpringBootApplication简单分析 进入SpringBootApplication源代码如下: 可以看出SpringBootApplication是…...
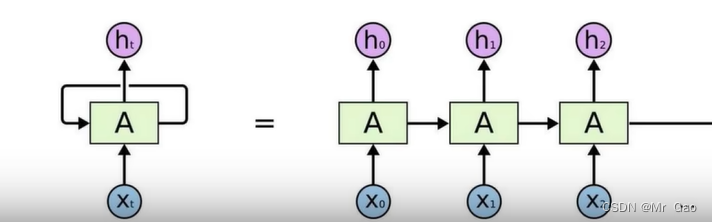
浅谈wor2vec,RNN,LSTM,Transfermer之间的关系
浅谈wor2vec,RNN,LSTM,Transfermer之间的关系 今天博主谈一谈wor2vec,RNN,LSTM,Transfermer这些方法之间的关系。 首先,我先做一个定位,其实Transfermer是RNN,LSTM&…...
【11】c++设计模式——>单例模式
单例模式是什么 在一个项目中,全局范围内,某个类的实例有且仅有一个(只能new一次),通过这个唯一的实例向其他模块提供数据的全局访问,这种模式就叫单例模式。单例模式的典型应用就是任务队列。 为什么要使…...
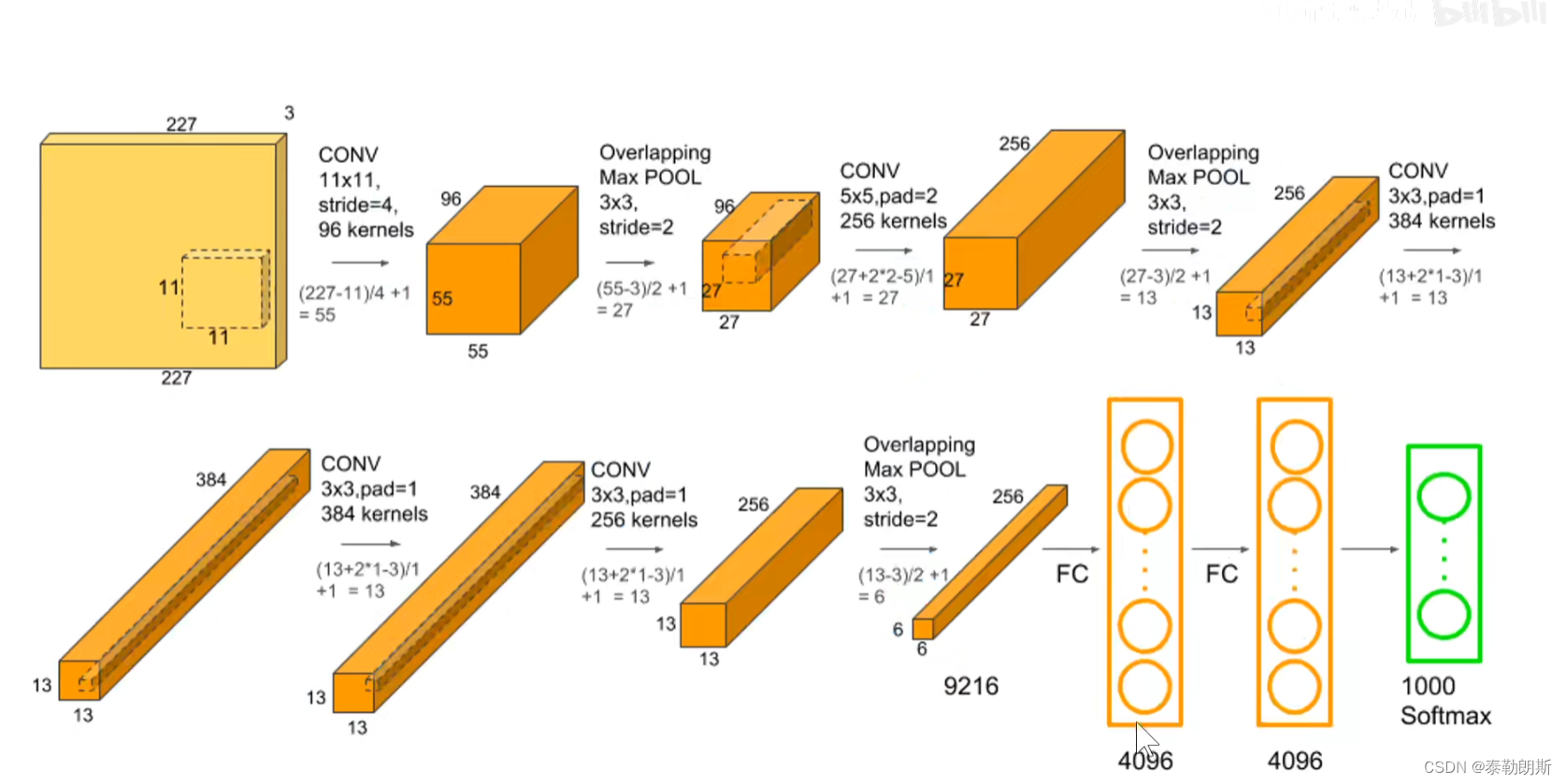
深度学习-卷积神经网络-AlexNET
文章目录 前言1.不同卷积神经网络模型的精度2.不同神经网络概述3.卷积神经网络-单通道4.卷积神经网络-多通道5.池化层6.全连接层7.网络架构8.Relu激活函数9.双GPU10.单GPU模型 1.LeNet-52.AlexNet1.架构2.局部响应归一化(VGG中取消了)3.重叠/不重叠池化4…...

人机关系不是物理关系也不是数理关系
人机关系是一种复杂的社会技术系统,涉及到人类和机器、环境之间的相互作用和影响。它不仅限于物理接触和数理规律,同时还包括了思维、情感、意愿等方面的交流和互动。在人机关系中,人类作为使用者和机器作为工具(将来可能会上升到…...

<html dir=ltr>是什么意思?
<html dirltr>的意思是: 文字默认从左到右排列 说明: HTML--超级文本标记语言 dir 属性 -- (文字的)排列方式属性 取值: ltr -- 代表左到右的排列方式 rtl -- 代表右到左的排列方式 默认值:ltr 示例: ltr左到右的对…...
)
工厂模式:简化对象创建的设计思想 (设计模式 四)
引言 在软件开发中,我们经常需要创建各种对象实例来满足不同的需求。通常情况下,我们会使用new关键字直接实例化对象,但这种方法存在一些问题,比如对象的创建逻辑分散在代码中,难以维护和扩展,同时也违反了…...

【2023最新】微信小程序中微信授权登录功能和退出登录功能实现讲解
文章目录 一、讲解视频二、小程序前端代码三、后端Java代码四、备注 一、讲解视频 教学视频地址: 视频地址 二、小程序前端代码 // pages/profile/profile.js import api from "../../utils/api"; import { myRequest } from "../../utils/reques…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...

作为测试我们应该关注redis哪些方面
1、功能测试 数据结构操作:验证字符串、列表、哈希、集合和有序的基本操作是否正确 持久化:测试aof和aof持久化机制,确保数据在开启后正确恢复。 事务:检查事务的原子性和回滚机制。 发布订阅:确保消息正确传递。 2、性…...

OD 算法题 B卷【正整数到Excel编号之间的转换】
文章目录 正整数到Excel编号之间的转换 正整数到Excel编号之间的转换 excel的列编号是这样的:a b c … z aa ab ac… az ba bb bc…yz za zb zc …zz aaa aab aac…; 分别代表以下的编号1 2 3 … 26 27 28 29… 52 53 54 55… 676 677 678 679 … 702 703 704 705;…...
