电路维修——双端队列BFS
达达是来自异世界的魔女,她在漫无目的地四处漂流的时候,遇到了善良的少女翰翰,从而被收留在地球上。
翰翰的家里有一辆飞行车。有一天飞行车的电路板突然出现了故障,导致无法启动。电路板的整体结构是一个 R 行 C 列的网格(R,C≤500),如下图所示。

每个格点都是电线的接点,每个格子都包含一个电子元件。电子元件的主要部分是一个可旋转的、连接一条对角线上的两个接点的短电缆。在旋转之后,它就可以连接另一条对角线的两个接点。电路板左上角的接点接入直流电源,右下角的接点接入飞行车的发动装置。
达达发现因为某些元件的方向不小心发生了改变,电路板可能处于断路的状态。她准备通过计算,旋转最少数量的元件,使电源与发动装置通过若干条短缆相连。不过,电路的规模实在是太大了,达达并不擅长编程,希望你能够帮她解决这个问题。
注意:只能走斜向的线段,水平和竖直线段不能走。
输入格式
输入文件包含多组测试数据。
第一行包含一个整数 T,表示测试数据的数目。
对于每组测试数据,第一行包含正整数 R 和 C,表示电路板的行数和列数。
之后 R 行,每行 C 个字符,字符是"/"和"\"中的一个,表示标准件的方向。
输出格式
对于每组测试数据,在单独的一行输出一个正整数,表示所需的最小旋转次数。
如果无论怎样都不能使得电源和发动机之间连通,输出 NO SOLUTION。
数据范围
1≤R,C≤500,1≤T≤5
输入样例:
1
3 5
\\/\\
\\///
/\\\\
输出样例:
1
样例解释
样例的输入对应于题目描述中的情况。
只需要按照下面的方式旋转标准件,就可以使得电源和发动机之间连通。

解析:
从(0,0) 走到 (n,m)的过程中,能走的边权为0,需要旋转的边权为1。
旋转最少数量的元件也就是从(0,0) 走到 (n,m)的最短距离。
这道题用的是双端队列BFS也可以说是特殊的 Dijkstra.
注意:对于每个点,它要走的下一个点只能是坐标和为偶数的点,也就是左上、右上、右下、左下。
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define ios ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
typedef pair<int,int> PII;
const int N=2e6+10;
deque <PII> q;
char g[510][510];
bool vis[510][510];
int d[510][510];
int n,m;
int dx[4]={-1,-1,1,1}; //该点下步的点(起点是(0,0),之后走的点就是坐标和为偶数的点),即左上、右上、右下、左下
int dy[4]={-1,1,1,-1};int ix[4]={-1,-1,0,0}; //该点下步的点的状态
int iy[4]={-1,0,0,-1};char c[5]="\\/\\/"; //该点下步的点的理想状态 (若权值为0的状态)
void bfs()
{memset(vis,0,sizeof vis);memset(d,0x3f,sizeof d);q.push_back({0,0});d[0][0]=0;while (q.size()){int x=q.front().first;int y=q.front().second;q.pop_front();if (vis[x][y]) continue;vis[x][y]=1;for (int i=0;i<4;i++){int a=x+dx[i],b=y+dy[i];if (a>=0&&a<=n&&b>=0&&b<=m){int ga=x+ix[i],gb=y+iy[i];int w=(g[ga][gb]!=c[i]);if (d[x][y]+w<=d[a][b]){d[a][b]=d[x][y]+w;if (w) q.push_back({a,b});else q.push_front({a,b});}}}}
}
signed main()
{ios;int t;cin>>t;while (t--){cin>>n>>m;for (int i=0;i<n;i++)for (int j=0;j<m;j++)cin>>g[i][j];if ((n+m)%2!=0) cout<<"NO SOLUTION\n"; //(n+m)如果是奇数,就走不到该点,即无解else {bfs();cout<<d[n][m]<<endl;}}return 0;
}相关文章:

电路维修——双端队列BFS
达达是来自异世界的魔女,她在漫无目的地四处漂流的时候,遇到了善良的少女翰翰,从而被收留在地球上。 翰翰的家里有一辆飞行车。有一天飞行车的电路板突然出现了故障,导致无法启动。电路板的整体结构是一个 R 行 C 列的网格&#…...
乌班图22.04 kubeadm简单搭建k8s集群
1. 我遇到的问题 任何部署类问题实际上对于萌新来说都不算简单,因为没有经验,这里我简单将部署的步骤和想法给大家讲述一下 2. 简单安装步骤 准备 3台标准安装的乌班图server22.04(采用vm虚拟机安装,ip为192.168.50.3࿰…...
vue3富文本编辑器的二次封装开发-Tinymce
欢迎点击领取 -《前端面试题进阶指南》:前端登顶之巅-最全面的前端知识点梳理总结 *分享一个使用比较久的🪜 简介 1、安装:pnpm add tinymce / pnpm add tinymce/tinymce-vue > Vue3 tinymce tinymce/tinymce-vue 2、功能实现图片上传…...
typescript 类型声明文件
typescript 类型声明文件概述 在今天几乎所有的JavaScript应用都会引入许多第三方库来完成任务需求。这些第三方库不管是否是用TS编写的,最终都要编译成JS代码,才能发布给开发者使用。6我们知道是TS提供了类型,才有了代码提示和类型保护等机…...
Hadoop伪分布式环境搭建
什么是Hadoop伪分布式集群? Hadoop 伪分布式集群是一种在单个节点上模拟分布式环境的配置,用于学习、开发和测试 Hadoop 的功能和特性。它提供了一个简化的方式来体验和熟悉 Hadoop 的各个组件,而无需配置和管理一个真正的多节点集群。 在 Ha…...
javaee ssm框架项目添加分页控件
搭建ssm框架项目 参考上一篇博文 添加分页控件 引入依赖 <?xml version"1.0" encoding"UTF-8"?><project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://www.w3.org/2001/XMLSchema-instance"xsi:schema…...
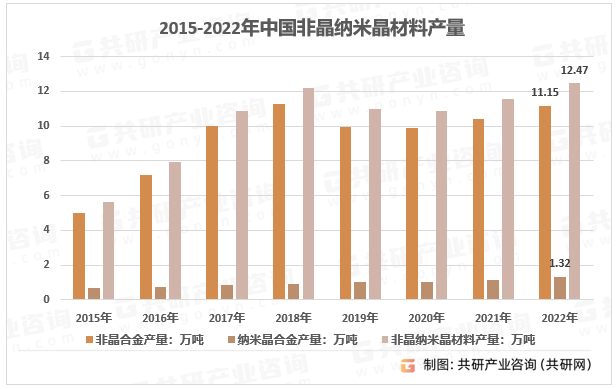
2023年中国非晶纳米晶竞争格局、产业链及行业产量分析[图]
非晶合金又称“液态金属、金属玻璃”,是一种新型软磁合金材料,主要包含铁、硅、硼等元素。其主要制品非晶合金薄带的制造工艺是采用急速冷却技术将合金熔液以每秒106℃的速度急速冷却,形成厚度约0.03mm的非晶合金薄带,物理状态表现…...
,递归处理。)
在业务开发中遇到的树形结构(部门、区域、职位),递归处理。
文章目录 概要对象结构示例完整示例小结 概要 本文主要记录在树形结构中会遇到的问题, 使用部门结构讲解,main方法进行演示。 1、获取部门树结构 2、根据部门id获取所有下级 3、根据部门id获取上级部门 4、根据部门id获取类似面包屑(总公司…...

张量-算术操作函数
tf.add(x,y,name None)求和函数 示例代码如下: import tensorflow.compat.v1 as tf tf.disable_v2_behavior()x 1 y 2a tf.add(x,y)with tf.Session() as sess:print(sess.run(a)) tf.subtract(x,y,name None)减法函数 示例代码如下: import tensorflow.compat.v1 as …...

虚拟展厅有什么重要意义,了解虚拟展厅在宣传中的应用
引言: 随着科技的不断进步,虚拟展厅已经逐渐成为展览行业的重要一环。虚拟展厅是一种数字化平台,为观众提供了与传统展览完全不同的体验。 一.虚拟展厅的定义 虚拟展厅是一个通过互联网和虚拟现实技术创建的数字展示空间&#x…...
)
华为OD机试真题-补种未成活胡杨(Java/C++/Go/Python)
华为OD机试真题-补种未成活胡杨(Java/C++/Go/Python) 题目描述 近些年来,我国防沙治沙取得显著成果。某沙漠新种植N棵胡杨(编号1-N),排成一排。 一个月后,有M棵胡杨未能成活。现可补种胡杨K棵,请问如何补种(只能补种,不能新种),可以得到最多的连续胡杨树? 输入…...
Java卷上天,可以转行干什么?
小刚是某名企里的一位有5年经验的高级Java开发工程师,每天沉重的的工作让他疲惫不堪,让他萌生出想换工作的心理,但是转行其他工作他又不清楚该找什么样的工作 因为JAVA 这几年的更新实在是太太太……快了,JAVA 8 都还没用多久&am…...

Pyside6 安装和简单界面开发
Pyside6 安装和简单界面开发 Pyside6介绍Pysied6开发环境搭建Python安装Pysied6安装 Pyside6界面开发简单界面设计界面设计界面编译 编写界面初始化代码软件打包 Pyside6介绍 对于Python的GUI开发来说,Python自带的可视化编程模块的功能较弱,PySide是跨…...
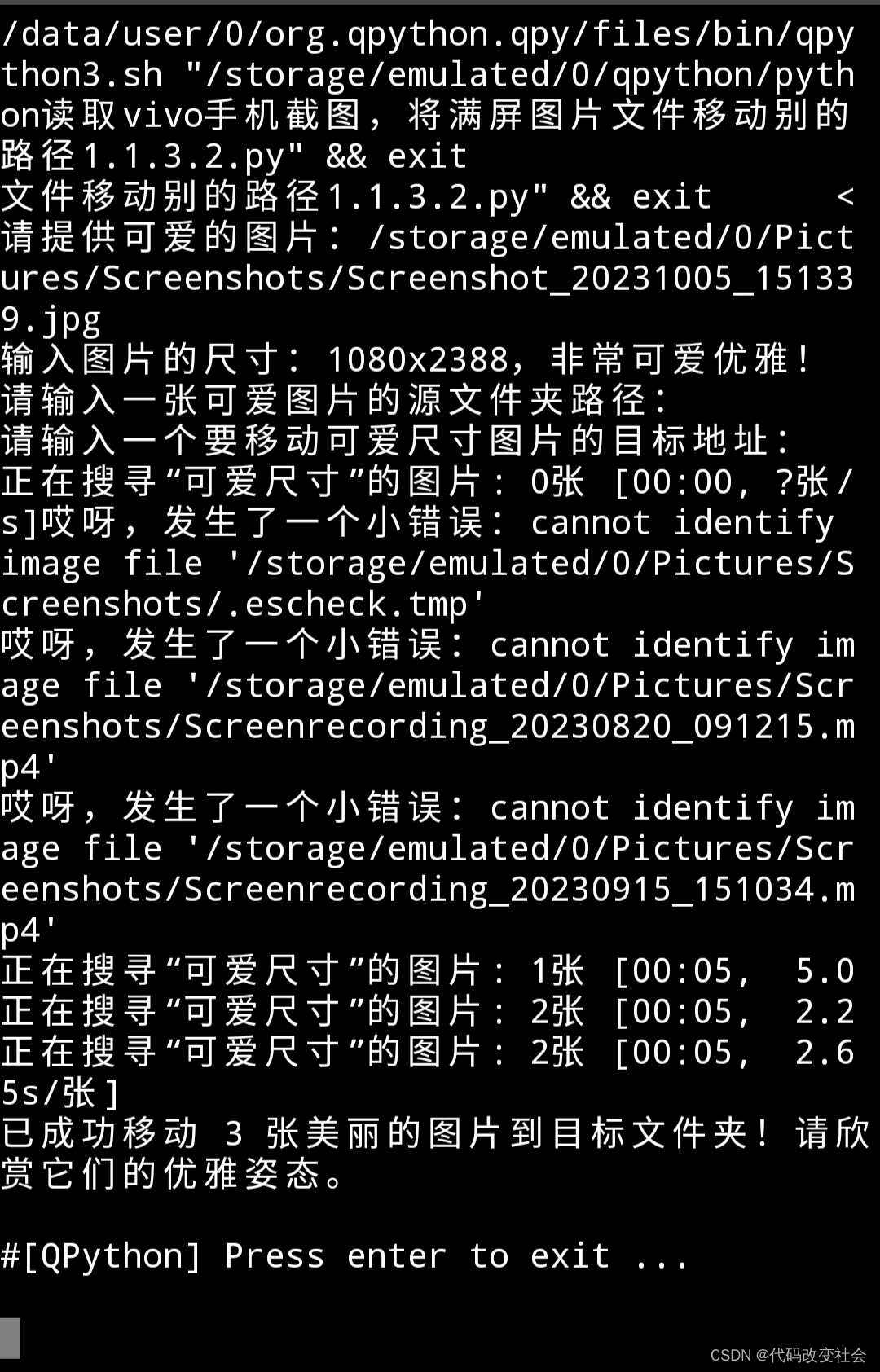
python读取vivo手机截图,将满屏图片文件移动别的路径
问题之初 python读取vivo手机截图, 将满屏图片文件移动别的路径好多这样的图片,占用手机大量的内存,食之无味弃之可惜!那么会复制粘贴👀代码的我们我们今天就把这些图片筛选清理掉。 这段代码 原有逻辑的基础上&…...

【一周安全资讯1007】多项信息安全国家标准10月1日起实施;GitLab发布紧急安全补丁修复高危漏洞
要闻速览 1.以下信息安全国家标准10月1日起实施 2.GitLab发布紧急安全补丁修复高危漏洞 3.主流显卡全中招!GPU.zip侧信道攻击可泄漏敏感数据 4.MOVEit漏洞导致美国900所院校学生信息发生大规模泄露 5.法国太空和国防供应商Exail遭黑客攻击,泄露大量敏感…...

2023年09月个人工作生活总结
本文为 2023 年 9 月工作生活总结。 研发编码 Alpine 容器 某工程部署于alpine镜像,当初看上是因为其体积小,其它微服务,在250MB左右,但那个工程只用50MB。最近发现时间戳转换不正确。对于同一时间字符串转时间戳函数࿰…...

现货白银图表分析的依据
现货白银的行情图表分析其实与股票的差不多,投资者可以结合均线、k线的变化,来分析实时的行情走势。当走势图的均线呈多头排列,即短期、中期、长期均线依次从上到下排列并向右上方运行,且白银价格沿各均线向右上方拉升,…...

python多线程与多进程
多线程与多进程 一, 什么是进程, 什么是线程? 进程: 运行中的程序. 每次我们执行一个程序, 咱们的操作系统对自动的为这个程序准备一些必要的资源(例如, 分配内存, 创建一个能够执行的线程. ) 线程: 程序内, 可以直接被CPU调度的执行过程. 是操作系统能够进行运算调度…...

62从零开始学Java之时间相关的类都有哪些?
作者:孙玉昌,昵称【一一哥】,另外【壹壹哥】也是我哦 千锋教育高级教研员、CSDN博客专家、万粉博主、阿里云专家博主、掘金优质作者 前言 我们在开发时,除了数字、数学这样的常用API之外,还有日期时间类,更…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

如何更改默认 Crontab 编辑器 ?
在 Linux 领域中,crontab 是您可能经常遇到的一个术语。这个实用程序在类 unix 操作系统上可用,用于调度在预定义时间和间隔自动执行的任务。这对管理员和高级用户非常有益,允许他们自动执行各种系统任务。 编辑 Crontab 文件通常使用文本编…...

