如何实现矩阵的重采样问题
文章目录
- 前言
- 一、问题描述
- 二、回答
前言
记录知乎的自问自答。
一、问题描述
我的问题是这样的,有两个列向量E和F,需要注意的是,E和F是连续的,可任意插值,得到包含其中的子向量。E和F通过一个m×n的矩阵联系起来,如下: M m × n × E n × 1 = F m × 1 M_{m\times n}\times E_{n\times 1}=F_{m\times 1} Mm×n×En×1=Fm×1现在,我通过线性插值的方式,得到了E和F的子向量,它们长度分别为v和u,那么请问,我该如何求得矩阵M’,使得: M u × v ′ × E v × 1 = F u × 1 M'_{u\times v}\times E_{v\times 1}=F_{u\times 1} Mu×v′×Ev×1=Fu×1
二、回答
可能是我表述不明白?或者这个问题比较简单?思考了两天,找到了在一定假设下能够实现我需求的方法,这里记录一下。
对于这种要采样的矩阵来说,最麻烦的是,每行的采样方式,因为这是一个相乘再求和的过程,在这个基础上,对结果进行插值,再求矩阵,不可避免地会产生问题。好在我这里的实际问题能够在有效的假设下,规避这个问题。
既然说,E和F都是连续的,不妨设存在函数E(x)和F(x)来描述这两个向量。我们从简单的地方出发,看看会遇到什么问题,先在行方向上采用,再处理列方向的采样。
首先,我们来计算F的第一行, F 1 = M 1 , 1 × E 1 + M 1 , 2 × E 2 + . . . + M 1 , n × E n = ∑ j = 1 n M 1 , j × E j F_1=M_{1,1}\times E_1+M_{1,2}\times E_2+...+M_{1,n}\times E_n=\sum_{j=1}^{n}{M_{1,j}}\times E_j F1=M1,1×E1+M1,2×E2+...+M1,n×En=∑j=1nM1,j×Ej。既然E和F都是连续的,那么不难推断,M应当也是连续的,可任意插值,不妨在第一行上,我们用m(x)表示。那么刚才的式子就可以写成 F 1 = ∫ 1 n m ( x ) E ( x ) d x F_1=\int_{1}^{n}m\left( x \right)E\left( x \right)dx F1=∫1nm(x)E(x)dx。
现在,我们期望的是,从E(x)中任意抽出的序列 E v × 1 E_{v\times 1} Ev×1,都能找到对应的m(x)的序列 M 1 × v ′ M'_{1\times v} M1×v′,继续满足 F 1 = ∑ j = 1 v M 1 , j ′ × E j F_1=\sum_{j=1}^{v}{M'_{1,j}}\times E_j F1=∑j=1vM1,j′×Ej。你可能想用拟合的方法求得m(x),但不幸的是,m(x)并没有你想的平缓,拟合容易出问题,而且我的问题对数值比较敏感,M矩阵的量级在 1 0 − 5 10^{-5} 10−5,贸然拟合恐怕会有比较大的偏差。相对于拟合,我更喜欢插值。
我们把视野再缩小一点,看看 E v × 1 E_{v\times 1} Ev×1中的某个 E i E_i Ei,如何通过插值获得其对应的 M 1 , i ′ M'_{1,i} M1,i′呢?不失一般性地,我们找到 M 1 , i ′ M'_{1,i} M1,i′在原始矩阵中临近的两个值m(a),m(b)和它们对应的E(a),E(b)。我们希望的是, ∫ a b m ( x ) E ( x ) d x = m ′ ( i ) × E ( i ) \int_{a}^{b}m\left( x \right)E\left( x \right)dx=m'\left( i \right)\times E\left( i \right) ∫abm(x)E(x)dx=m′(i)×E(i),这时,我们重要的假设就要登场了。
好在,在一个a-b的区间内,可以合理假设E是不变的,或者,该积分的值主要受m(x)影响,那么上面的式子就变成了 ∫ a b m ( x ) d x = m ′ ( i ) \int_{a}^{b}m\left( x \right)dx=m'\left( i \right) ∫abm(x)dx=m′(i)。至此,通过合理的假设,完成了M’在行方向上的采样。
那么继续,在列方向上的采样就简单得多了,直接线性插值即可,因为矩阵的每一行之间没有计算。
解决这个问题稍显兴奋,写得有些啰里吧嗦,感谢您能浪费时间在这个问题上。
相关文章:

如何实现矩阵的重采样问题
文章目录 前言一、问题描述二、回答 前言 记录知乎的自问自答。 一、问题描述 我的问题是这样的,有两个列向量E和F,需要注意的是,E和F是连续的,可任意插值,得到包含其中的子向量。E和F通过一个mn的矩阵联系起来&…...
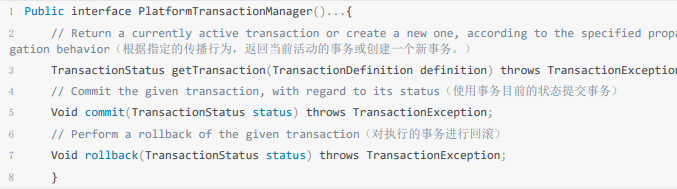
Spring-事务管理-加强
目录 开启事务 编程式事务 声明式事务 声明式事务的优点 声明式事务的粒度问题 声明式事务用不对容易失效 Spring事务失效可能是哪些原因 Transactional(rollbackFor Exception.class)注解 Spring 事务的实现原理 事务传播机制 介绍 用法 rollbackFor 场景举例 …...

Minecraft个人服务器搭建自己的皮肤站并实现外置登录更换自定义皮肤组件
Minecraft个人服务器搭建自己的皮肤站并实现外置登录更换自定义皮肤组件 大家好,我是艾西有不少小伙伴非常喜欢我的世界Minecraft游戏,今天小编跟大家分享下Minecraft个人服务器怎么设置皮肤站。 Minecraft皮肤站是什么?其实官网就有皮肤站…...
解决ubuntu中没有网络连接的图标
现象:Ubuntu连接网络 在设置中没有显示网络图标 解决方案: 命令为 sudo nmcli networking off sudo nmcli networking on sudo service network-manager restart 重启ubuntu,网络连接完成...
数据结构基本概念-Java常用算法
数据结构基本概念-Java常用算法 1、数据结构基本概念2、数据逻辑结构3、算法时间复杂度 1、数据结构基本概念 数据(Data):数据是信息的载体,其能够被计算机识别、存储和加工处理,是计算机程序加工的“原材料”。数据元…...

流程图设计制作都有哪些好用的工具
流程图是一种直观的图形表示方式,通常用于显示事物的过程、步骤和关系。在现代工作中,设计师经常需要绘制各种流程图来解释工作过程、产品设计等。本文将为您推荐7个流程图软件,以帮助您快速绘制高效的流程图,并提高工作效率。 即…...

2023-10-7
今日感冒了,整个人都不舒服,现在才 8 点,已经不想学习了。嗓子眼感觉不属于我了,痛死了。然后头也晕。 哎,今天又啥也没干 今日学习: 哎,今天就做了 RWCTF2022-Digging-into-kernel-2 这道题…...
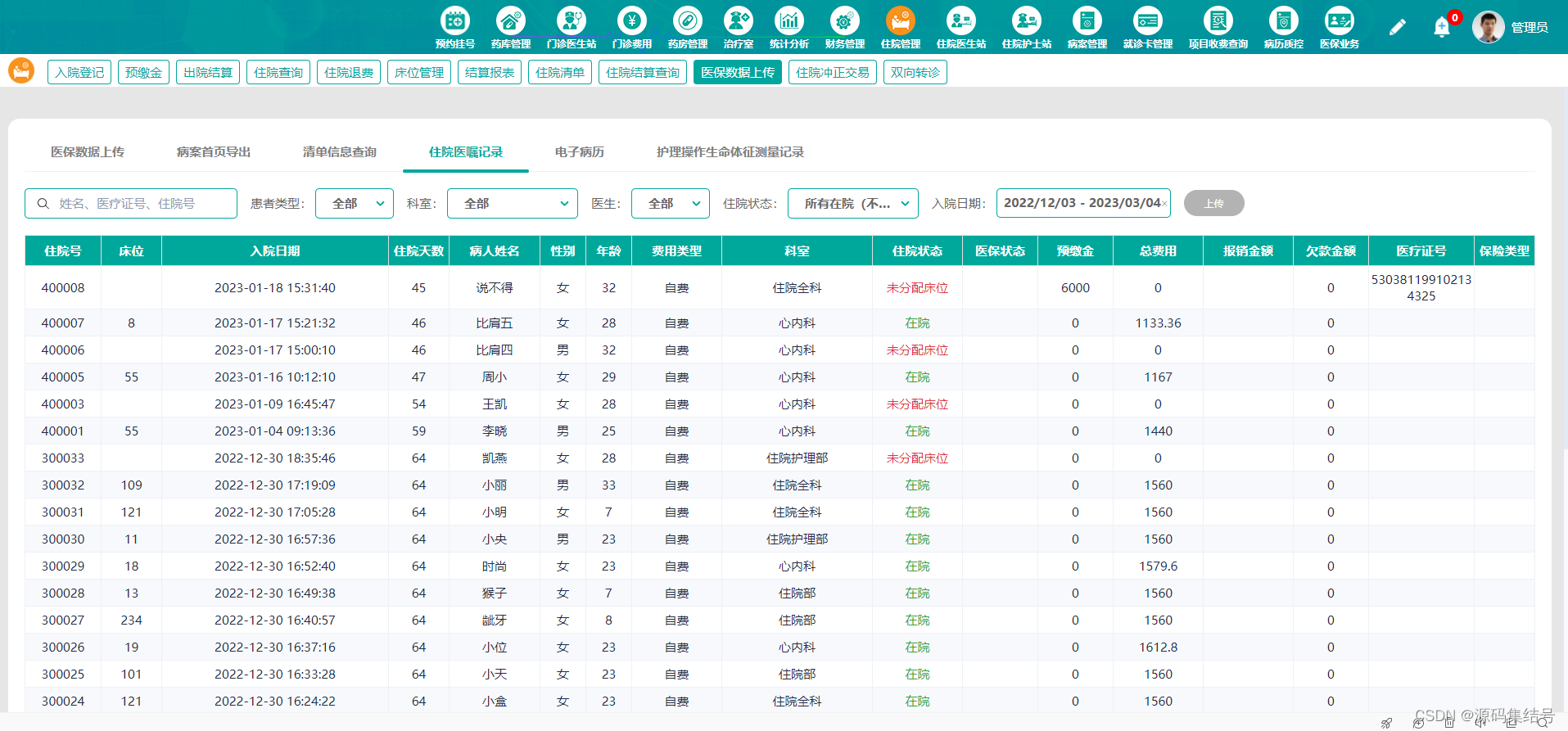
【java源码】二甲医院his系统全套源码 云HIS系统源码
基层医院云HIS系统源码 一款满足基层医院各类业务需要的云HIS系统。该系统能帮助基层医院完成日常各类业务,提供病患挂号支持、病患问诊、电子病历、开药发药、会员管理、统计查询、医生站和护士站等一系列常规功能,还能与公卫、PACS等各类外部系统融合&…...

LRU 缓存 -- 哈希链表
相关题目 146. LRU 缓存 要让 put 和 get ⽅法的时间复杂度为 O(1),我们可以总结出 cache 这个数据结构必要的条件: 1、显然 cache 中的元素必须有时序,以区分最近使⽤的和久未使⽤的数据,当容量满了之后要删除最久未使⽤的那个元…...

DWC数字世界大会先导论坛将于10月13日在宁波举办 | 数字技术赋能世界可持续发展
农业经济影响世界数千年,工业经济从欧美发源开始已有数百年,数字经济作为世界未来发展之大势,将成为影响未来数百年的世界命题。在以中国式现代化全面推进中华民族伟大复兴的历史征程中,数字技术、数字经济作为中国式现代化实践最…...

Springboot实现登录功能(token、redis、登录拦截器、全局异常处理)
登录流程: 1、前端调用登录接口,往接口里传入账号,密码 2、根据账号判断是否有这个用户,如果有则继续判断密码是否正确 3、验证成功后,则是根据账号,登录时间生成token(用JWT) 4、将…...

AI工程化—— 如何让AI在企业多快好省的落地?
文章目录 前言内容简介读者对象专家推荐目录赠书活动 前言 作为计算机科学的一个重要领域,机器学习也是目前人工智能领域非常活跃的分支之一。机器学习通过分析海量数据、总结规律,帮助人们解决众多实际问题。随着机器学习技术的发展,越来越多…...

mysqld_multi测试
mysqld_multi测试 mysql版本:5.7.25-log 在OS上分别安装了两套mysql, data目录为/mysql/mysql3306、 /mysql/mysql3307 。 端口分别为3306 、3307 配置文件为: /mysql/mysql3306/my.cnf /mysql/mysql3307/my.cnf 参考文档: htt…...

MDC方式实现简单链路追踪
MDC 方式实现日志链路追踪 拦截器 package com.cdn.log.interceptor;import com.cdn.log.consts.CLogConst; import com.cdn.log.utils.IdUtil; import org.slf4j.MDC; import org.springframework.util.StringUtils; import org.springframework.web.servlet.ModelAndView; im…...

Linux深度学习:除基本命令操作外的实用操作
Linux深度学习:除基本命令操作外的实用操作 软件安装systemctl软连接日期、时区IP地址、主机名网络传输下载和网络请求端口 进程管理主机状态系统资源监控磁盘信息监控网络状态监控 环境变量上传、下载压缩、解压root用户、用户、用户组管理查看、修改权限控制 软件…...

app对接广告变现平台:影响app广告单价的4大因素
在移动应用开发者和媒体公司竞相寻求提高广告变现效率的今天,理解影响APP广告单价的关键因素至关重要。广告单价是广告收入的核心组成部分,它受多种因素的影响,直接关系到媒体的盈利能力。主要因素大概有以下几点:#APP广告变现# …...
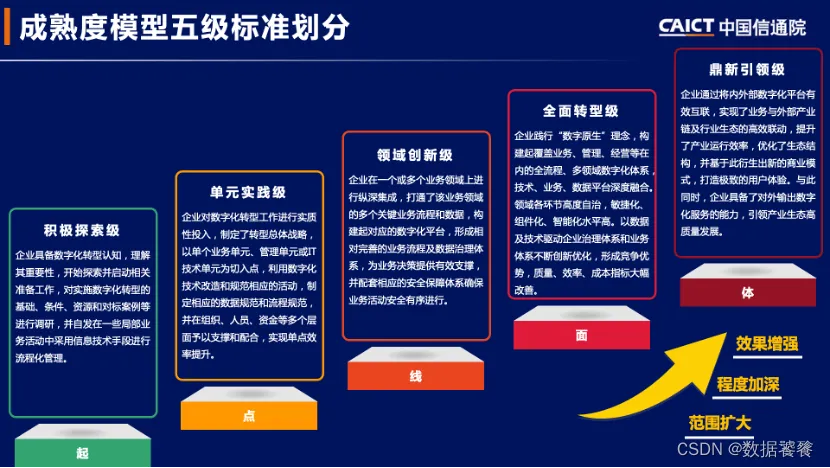
【数字化转型】10大数字化转型能力成熟度模型01(IOMM)
一、前言 数字化转型是数据化能力建设的目标和价值,作为一个新兴的课题,目前为止并未出现一个统一的数字化转型成熟度模型。不同的企业和机构,根据自身的发展和认知,推出了自己的企业级或者准行业级标准。这些标准具有很强的参考意…...

2023腾讯云轻量应用服务器和普通服务器有什么区别?
腾讯云轻量服务器和云服务器有什么区别?为什么轻量应用服务器价格便宜?是因为轻量服务器CPU内存性能比云服务器CVM性能差吗?轻量应用服务器适合中小企业或个人开发者搭建企业官网、博客论坛、微信小程序或开发测试环境,云服务器CV…...

SSL证书是什么?1分钟get
在当今互联网世界中,保护数据的完整性和隐私性至关重要,由此,在网络数据安全保护领域,作为保护网络传输数据安全的SSL证书越来越频繁出现。那么你知道SSL证书是什么?SSL证书有哪些类型?SSL证书有什么用吗&a…...

3D打印机升级killpper
本来是想整台新机的,但是想想老机器4max也不能就此放弃,看了看视频,改装升级似乎也没有那么难。然后就是换了喷头、皮带、轴承、挤出机、打印平台、加热板等等。做了干燥箱,改装挤出机结构来适配,风扇口也一并搞掉&…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...

【MATLAB代码】基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),附源代码|订阅专栏后可直接查看
文章所述的代码实现了基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),针对传感器观测数据中存在的脉冲型异常噪声问题,通过非线性加权机制提升滤波器的抗干扰能力。代码通过对比传统KF与MCC-KF在含异常值场景下的表现,验证了后者在状态估计鲁棒性方面的显著优…...

MacOS下Homebrew国内镜像加速指南(2025最新国内镜像加速)
macos brew国内镜像加速方法 brew install 加速formula.jws.json下载慢加速 🍺 最新版brew安装慢到怀疑人生?别怕,教你轻松起飞! 最近Homebrew更新至最新版,每次执行 brew 命令时都会自动从官方地址 https://formulae.…...

Ubuntu系统复制(U盘-电脑硬盘)
所需环境 电脑自带硬盘:1块 (1T) U盘1:Ubuntu系统引导盘(用于“U盘2”复制到“电脑自带硬盘”) U盘2:Ubuntu系统盘(1T,用于被复制) !!!建议“电脑…...

电脑桌面太单调,用Python写一个桌面小宠物应用。
下面是一个使用Python创建的简单桌面小宠物应用。这个小宠物会在桌面上游荡,可以响应鼠标点击,并且有简单的动画效果。 import tkinter as tk import random import time from PIL import Image, ImageTk import os import sysclass DesktopPet:def __i…...

如何通过git命令查看项目连接的仓库地址?
要通过 Git 命令查看项目连接的仓库地址,您可以使用以下几种方法: 1. 查看所有远程仓库地址 使用 git remote -v 命令,它会显示项目中配置的所有远程仓库及其对应的 URL: git remote -v输出示例: origin https://…...
