POJ 3264 Balanced Lineup 线段树 / 平方分割
一、题目大意
给出一个长度为 n(n<=50000) 数组 arr,进行Q次查询(Q<=200000),每次查询的内容为数组arr在 [L , R] 的切片的极差(最大元素 - 最小元素)
二、解题思路
1、线段树
区间极差其实就是 区间内最大值 - 区间内最小,那么就想到RMQ,用线段树去维护一个区间内的最大和最小元素,然后根据问题的区间 L 和 R,找到相关的线段树节点,从中找出 最大值最大的,然后减去最大值 最小的即可。
实现的方式就非常简单了,因为是线段树,所以就把叶子节点的数量扩展到满足 2^i >= n_的最小i的2^i,然后给那些多扩展出来的节点的最小值设置成无穷大,最大值设置成负无穷大,则不会影响线段树计算
设一开始输入的规模为n_,然后线段树叶子节点数量为n(一定需要为2的次幂),设输入的数组为num,线段树最大值datMax,最小值为datMin,为计算叶子节点对应的数组下标,可以用 i - n + 1,其中 i 是线段树节点的下标, i - n + 1是数组的下标,对于i - n + 1<n_ 的datMax[i]=num[i-n+1],datMin[i]=num[i-n+1],对于 i - n + 1 >= n_的,datMax[i]= (-1) * inf,datMin[i]= inf
然后计算父节点的时候,那就 datMin[i]=min(datMin[i * 2 + 1] , datMin[i * 2 + 2]),datMax[i]=max(datMax[i * 2 + 1] , datMax[i * 2 + 2])即可。
然后判断是否为叶子节点,就看 i 是不是大于 n - 1即可(n不是输入的规模,而是大于输入规模n_的第一个 2^i)
构建树的时候从 i=2*n-2;i>=0;i--即可。
然后查询L R的时候,只需要从根节点开始进行如下三个步骤,可以设最终用到的最小值为mint,最大值为maxt,然后设置mint=inf,maxt=inf * (-1)
1、节点 i 的区间如果与 L 和 R 毫无关联,则return
2、节点 i 区间被 L 和 R 完全包含,则mint=min(datMin[i],mint),maxt=max(datMax[i],maxt)
3、节点 i 与区间有重合部分,但不完全包含,递归 i * 2 + 1 和 i * 2 + 2
然后输出 maxt - mint即可解题
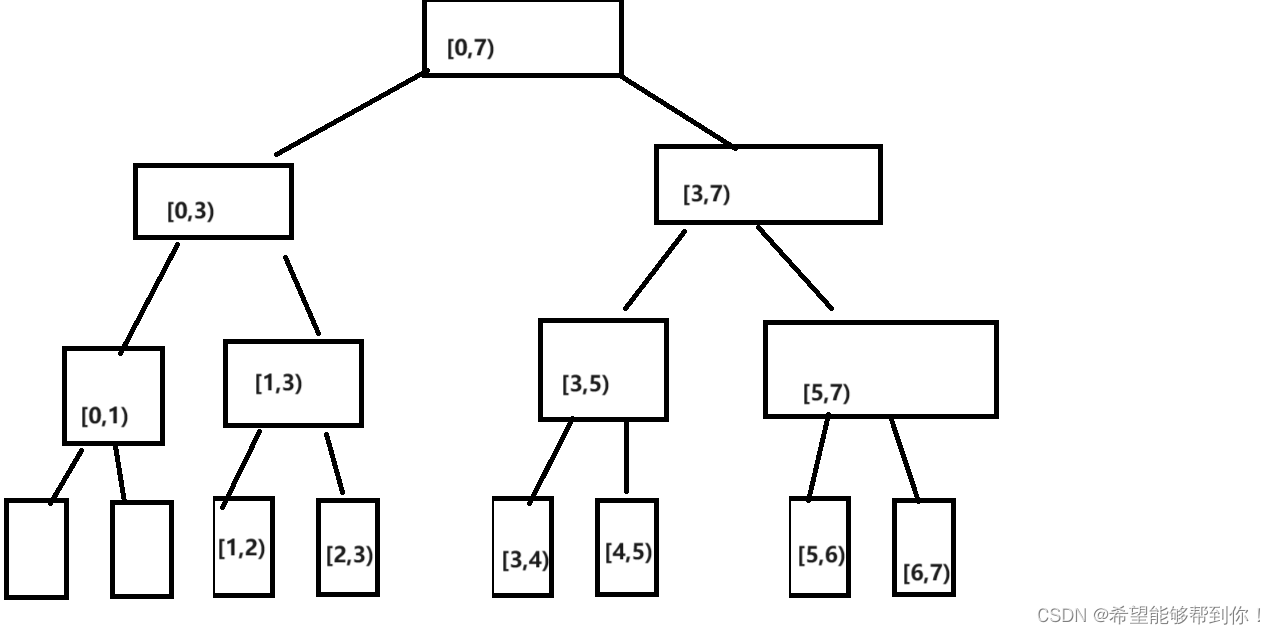
我写线段树时候,比较喜欢直接用数组,然后每个节点维护的区间为 左闭右开,比如 [0,1) [0,2) [0,4),然后我习惯于把最大区间弄成 2 的次幂,之后用无穷大和负无穷大来补充不足的值 ,之后区间通过调用方法时的参数传递,根节点 0 的区间为 [0 , n),然后如果节点 i 的区间为[L , R],则它左孩子 i * 2 + 1的区间为[0 , (L + R) / 2] ,右孩子的区间为 [(L + R) / 2, R),如果叶子节点数量时2的次幂,这个区间的计算可以通过画个图看出来 ,如下图所示。

然后另外补充一点,我觉得线段树叶子大小还是要扩充到2^i,不然叶子节点的赋值容易出问题,就是用循环方式,从2*n - 2到0用i-- 初始化的时候,一定会出问题,如下所示。
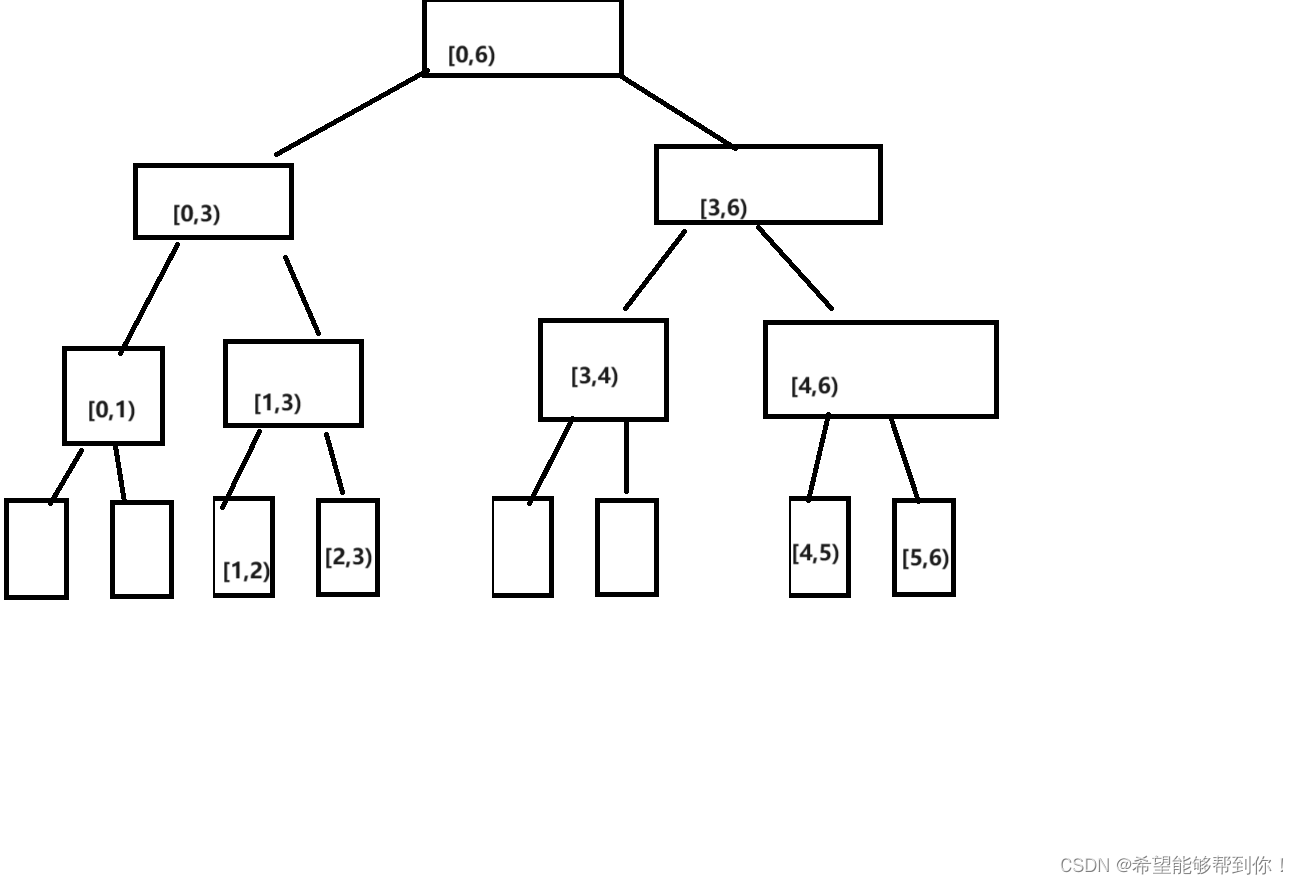
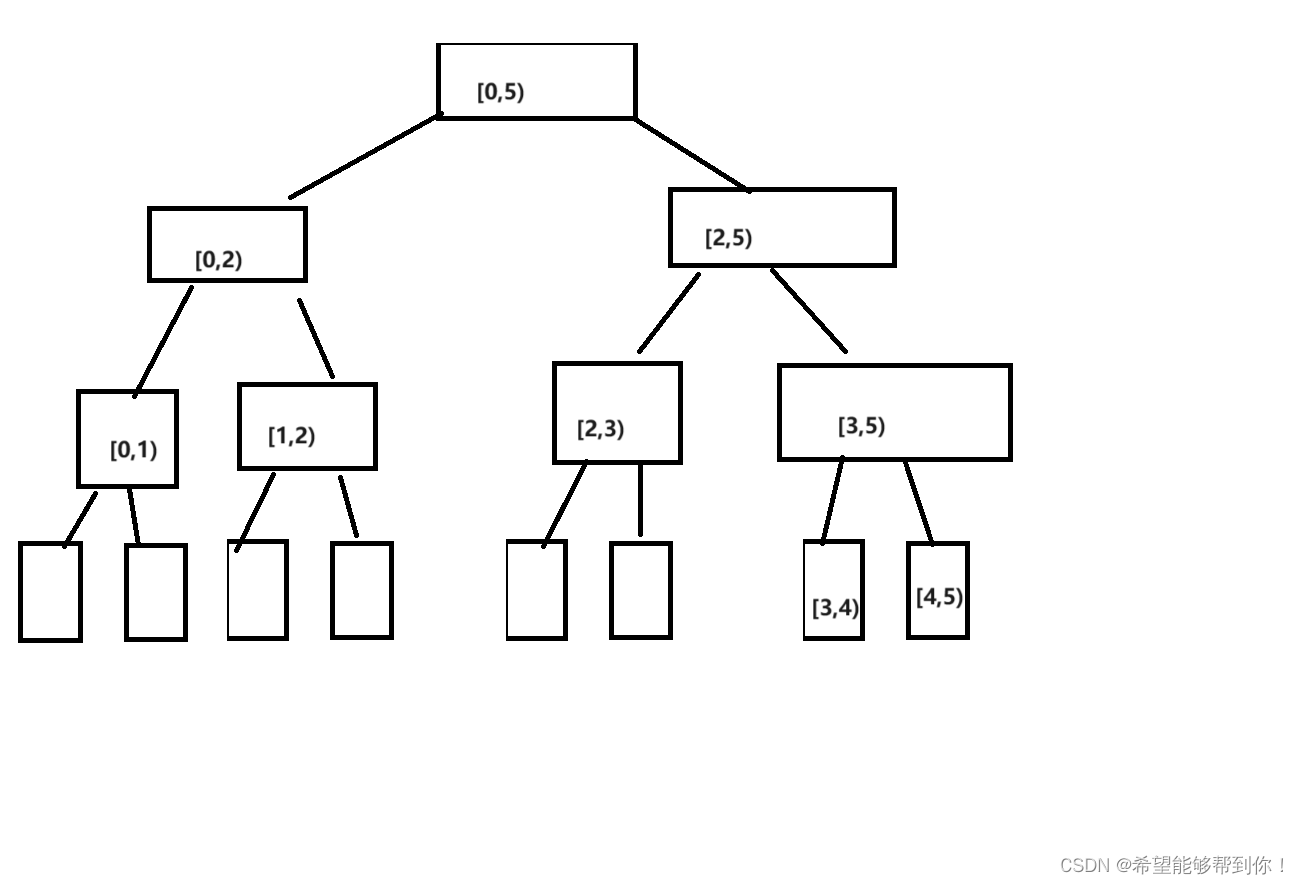
因为叶子节点不一定是下标最大的几个节点,也不一定是 i >= n - 1的节点,所以循环方式初始化有问题,但是使用递归初始化的话,不会有问题,而且代码看起来更精简。
不过还是建议把线段树的叶子节点扩充到最接近的 2的次幂,这样的话每一层的节点维护的区间是一样长的,更规范。
2、平方分割
平方分割的话,就简单很多了,我计算了下 根号 50000是 224再多一点,所以直接定义230个桶,设桶的大小为根号n下取整,定义为B,然后第 i 个桶维护的区间是 [i * B,(i + 1) * B),如果 i * B < n,但是 (i + 1) * B大于 n 时,那么桶 i 维护的区间为 [ i * B , n),然后维护每个桶的最大值和最小值。
设每个桶的最小值bucketMin,最大值为bucketMax,最开始把满足 i * B < n范围内所有的bucketMax[i]=inf*(-1),bucketMin[i]=inf,(我将区间从0开始,左闭右开,则n-1为最后一个有效位置,当i * B == n则,代表第 i 个桶的起点维护的是数组里不存在的元素,所以 i * B < n为范围)初始化的时候,只需用 i 循环 num 数组
1、bucketMax[i / B]=max(bucketMax[i / B] , num[i])
2、bucketMin[i / B]=max(bucketMin[i / B] , num[i])
然后对于每一次输入的 [L , R]区间,我们把它变成左闭右开,初始位置从0开始,即 L--,R不变,然后设置两个变量 mint = inf,maxt= inf * (-1)(inf是无穷大,定义成 0x3f3f3f3f就行)
用一个数组bucketQue记录包含在区间里的桶,设它的长度为queLen,初始化为 0
在 i * B < n 的范围内循环所有的桶,计算桶的区间左边bucketL = i * B,区间右边 bucketR = (i + 1)*B,然后bucketR > n 时,bucketR = n,如果 [bucketL , bucketR)被 [L , R)完全包含,则
1、mint = min(mint , bucketMin[i])
2、maxt = max(maxt , bucketMax[i])
3、bucketQue[queLen++] = i
然后处理不在桶内的区间,如果 queLen==0,则区间内不完整包含任何一个桶,则循环 [L , R)
1、mint = min(mint , num[i])
2、maxt = max(maxt ,num[i])
如果queLen>0,则循环 [L , bucketQue[0] * B) 和 [(bucketQue[queLen - 1] + 1) * B) , R)
1、mint = min(mint , num[i])
2、maxt = max(maxt ,num[i])
不难看出,bucketQue[0]是第一个桶,bucketQue[0] * B是第一个桶的起点(包含)
bucketQue[queLen - 1]是最后一个桶,bucketQue[queLen - 1]是最后一个桶的终点(不包含)
所以这两段左闭右开的区间是不包含在桶内的,而且在区间内的边缘,需要计算。
然后输出 maxt - mint即可。
三、代码
1、线段树(循环方式初始化,初始化叶子节点大小为 2的次幂)
#include <iostream>
using namespace std;
int datTall[131080], datShort[131080], n, n_, num[50007], inf = 0x3f3f3f3f, minShort, maxTall;
void input()
{for (int i = 0; i < n_; i++){scanf("%d", &num[i]);}
}
void init()
{n = 1;while (n < n_){n = n * 2;}for (int i = (2 * n - 2); i >= 0; i--){if (i >= (n - 1)){if ((i - n + 1) < n_){datTall[i] = num[i - n + 1];datShort[i] = num[i - n + 1];}else{datTall[i] = -inf;datShort[i] = inf;}}else{int lch = i * 2 + 1;int rch = i * 2 + 2;datTall[i] = max(datTall[lch], datTall[rch]);datShort[i] = min(datShort[lch], datShort[rch]);}}
}
void query(int l_, int r_, int i, int l, int r)
{if (l_ >= r || r_ <= l){}else if (l >= l_ && r <= r_){minShort = min(minShort, datShort[i]);maxTall = max(maxTall, datTall[i]);}else{query(l_, r_, i * 2 + 1, l, (l + r) / 2);query(l_, r_, i * 2 + 2, (l + r) / 2, r);}
}
int main()
{int m, L, R;scanf("%d%d", &n_, &m);input();init();while (m--){scanf("%d%d", &L, &R);minShort = inf;maxTall = -inf;query(L - 1, R, 0, 0, n);printf("%d\n", maxTall - minShort);}return 0;
}2、平方分割
#include <iostream>
#include <algorithm>
using namespace std;
int datTall[230], datShort[230], num[50007], n, B, inf = 0x3f3f3f3f, bucketQue[230], queLen;
void input()
{B = 1;while (B * B <= n){B++;}B--;for (int i = 0; (i * B) < n; i++){datTall[i] = -inf;datShort[i] = inf;}for (int i = 0; i < n; i++){scanf("%d", &num[i]);datTall[i / B] = max(datTall[i / B], num[i]);datShort[i / B] = min(datShort[i / B], num[i]);}
}
void solve(int L, int R)
{queLen = 0;int minTall = inf, maxTall = -inf;for (int i = 0; (i * B) < n; i++){int bucketL = i * B;int bucketR = (i + 1) * B;bucketR = (bucketR > n ? n : bucketR);if (bucketL >= L && bucketR <= R){bucketQue[queLen++] = i;minTall = min(minTall, datShort[i]);maxTall = max(maxTall, datTall[i]);}}if (queLen == 0){for (int i = L; i < R; i++){minTall = min(minTall, num[i]);maxTall = max(maxTall, num[i]);}}else{for (int i = L; i < (bucketQue[0] * B); i++){minTall = min(minTall, num[i]);maxTall = max(maxTall, num[i]);}for (int i = ((bucketQue[queLen - 1] + 1) * B); i < R; i++){minTall = min(minTall, num[i]);maxTall = max(maxTall, num[i]);}}printf("%d\n", maxTall - minTall);
}
int main()
{int m, L, R;scanf("%d%d", &n, &m);input();while (m--){scanf("%d%d", &L, &R);solve(L - 1, R);}return 0;
}3、线段树(递归方式初始化,非完美二叉树,代码简洁)
#include <istream>
using namespace std;
int datShort[131080], datTall[131080], n, num[50009], inf = 0x3f3f3f3f, mint, maxt;
void input()
{for (int i = 0; i < n; i++){scanf("%d", &num[i]);}
}
void build(int i, int l, int r)
{if (r - l == 1){datShort[i] = num[l];datTall[i] = num[l];}else{int lch = i * 2 + 1;int rch = i * 2 + 2;build(lch, l, (l + r) / 2);build(rch, (l + r) / 2, r);datShort[i] = min(datShort[lch], datShort[rch]);datTall[i] = max(datTall[lch], datTall[rch]);}
}
void query(int l_, int r_, int i, int l, int r)
{if (l_ >= r || r_ <= l){}else if (l >= l_ && r <= r_){mint = min(mint, datShort[i]);maxt = max(maxt, datTall[i]);}else{query(l_, r_, i * 2 + 1, l, (l + r) / 2);query(l_, r_, i * 2 + 2, (l + r) / 2, r);}
}
int main()
{int m, L, R;scanf("%d%d", &n, &m);input();build(0, 0, n);while (m--){scanf("%d%d", &L, &R);mint = inf, maxt = -inf;query(L - 1, R, 0, 0, n);printf("%d\n", maxt - mint);}return 0;
}相关文章:

POJ 3264 Balanced Lineup 线段树 / 平方分割
一、题目大意 给出一个长度为 n(n<50000) 数组 arr,进行Q次查询(Q<200000),每次查询的内容为数组arr在 [L , R] 的切片的极差(最大元素 - 最小元素) 二、解题思路 1、线段树 区间极差…...

element-plus自动引入组件报错,例如collapse、loading
element-plus自动引入组件,例如collapse、loading,使用时报错,报错信息如下图所示: 解决办法:vite-config.ts改变vue的引入顺序,将vue放在第一个...
ChainForge:衡量Prompt性能和模型稳健性的GUI工具包
ChainForge是一个用于构建评估逻辑来衡量模型选择,提示模板和执行生成过程的GUI工具包。ChainForge可以安装在本地,也可以从chrome浏览器运行。 ChainForge可以通过聊天节点对多个对话可以使用不同的llm并行运行。可以对聊天消息进行模板化,并…...

队列--二叉树层序遍历
/*1/ \2 3/\ /\4 5 6 7利用LinkedListQueue1. 头 [1] 尾12.头 [2 3] 尾1 23.头 [3 4 5] 尾1 24.头 [4 5 6 7] 尾1 2 35.头 [] 尾1 2 3 4 5 6 7*/ 代码: class Solution {public List<List<Integer>> levelOrder(TreeNode root) {List<List&l…...

Ceph入门到精通-Linux内核网络参数优化小结
tcp建连优化 1 tcp建连,降低客户端超时时间 net.ipv4.tcp_syn_retries 6 2 tcp建连,服务端避免syn攻击 netstat -s | grep "SYNs to LISTEN" 1192450 SYNs to LISTEN sockets dropped 可以考虑增大syn队列 net.ipv4.tcp_max_syn_backlo…...

AWK语言第二版 2.6个人库 2.7小结
2.6 个人库 Awk提供了适量的内置函数库,如 length、sub、substr、printf 等其他十来个;在A.2.1节的参考手册中都有列出。你可以自己创建更多函数,以便有需要时引入到Awk程序中。比如内置库函数 sub 和 gsub 都只能返回替换的次数,…...
8年经验之谈 —— Web ui自动化测试框架总结!
实施过了web系统的UI自动化,回顾梳理下,想到什么写什么,随时补充。 首先,自动化测试不是手动测试的替代品,是比较好的补充,而且不是占大比重的补充。 70%的测试工作集中在底层接口测试和单元测试࿰…...

Kafka在企业级应用中的实践
前言 前面说了很多Kafka的性能优点,有些童鞋要说了,这Kafka在企业开发或者企业级应用中要怎么用呢?今天咱们就来简单探究一下。 1、 使用 Kafka 进行消息的异步处理 Kafka 提供了一个可靠的消息传递机制,使得企业能够将不同组件…...
使用企业订货系统后的效果|软件定制开发|APP小程序搭建
使用企业订货系统后的效果|软件定制开发|APP小程序搭建 企业订货系统是一种高效的采购管理系统,它可以帮助企业更好地管理采购流程,降低采购成本,提高采购效率。 可以帮助企业提高销售效率和降低成本的软件工具。使用该系统后,企业…...

STL关联式容器set,multiset,pair,map
set容器是一个集合容器。包含元素是唯一的。集合元素按照一点顺序排列,元素插入过程是顺序插入,所有不能插入指定位置。 set采用红黑树变体的数据结构实现。红黑树属于平衡二叉树。再插入和删除上比vector快。 set不能直接存取元素(不能用a…...
MFC文本输出学习
void CTxttstView::OnDraw(CDC* pDC) {CTxttstDoc* pDoc GetDocument();ASSERT_VALID(pDoc);// TODO: add draw code for native data hereCString str1;pDC->SetBkColor(RGB(0,0,0));pDC->TextOut(50, 50, "一段文字");pDC->SetBkColor(RGB(255,255,255))…...

Python 数据分析与挖掘(一)
Python 数据分析与挖掘(数据探索) 数据探索 1.1 需要掌握的工具(库) 1.1.1 Nump库 Numpy 提供多维数组对象和各种派生对象(类矩阵),利用应用程序接口可以实现大量且繁琐的数据运算。可以构建…...

【问题证明】矩阵方程化为特征值方程求得的特征值为什么是全部特征值?不会丢解吗?
问题 这个问题困扰了我好久,一直感觉如果有其他的特征值没法证伪,不过一直存在思想的层面,没有实际解决,今天突然想到动笔来解决,遂得解,证明如下。 证明 总结 这个证明看似证明过后很直观,但…...
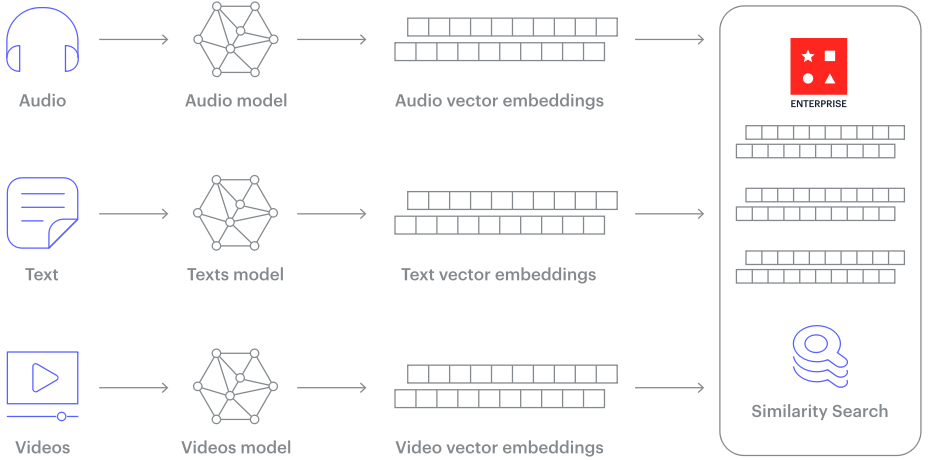
虹科干货 | 不是吧,Redis Enterprise也能当向量数据库来用?
什么是向量相似性搜索啊? 例如,你需要搜索一棵发财树的图片,如果用传统数据库来检索,你大概率会在茫茫树丛中错失心仪的发财树。但是,向量相似性搜索能用向量来表示所有树的特征,这样就能够通过计算向量之间…...

汽车驾驶 - 四梁六柱是什么
汽车的四梁六柱指的是车辆的两个前纵梁,两个后纵梁和ABC柱。虽然不像车辆上的发动机变速箱这些部件出镜率那么高,但这几个部位的重要作用可一点都不含糊。一辆车在碰撞时能够受力起到保护左右的就是四梁六柱,对我们汽车的安全性起到至关重要的…...

CI522 13.56MHZ电动车NFC测试资料
Ci522是一颗工作在13.56MHz频率下的非接触式读写芯片,支持读A卡(CI523支持读A/B卡),可做智能门锁、电动车NFC一键启动、玩具NFC开锁等应用。为部分要求低成本,PCB小体积的产品提供了可靠的选择。 Ci522与Si522/MFRC52…...

【微信小程序开发】一文学会使用CSS样式布局与美化
引言 在微信小程序开发中,CSS样式布局和美化是非常重要的一部分,它能够为小程序增添美感,提升用户体验。本文将介绍如何学习使用CSS进行样式布局和美化,同时给出代码示例,帮助开发者更好地掌握这一技巧。 一、CSS样式布…...
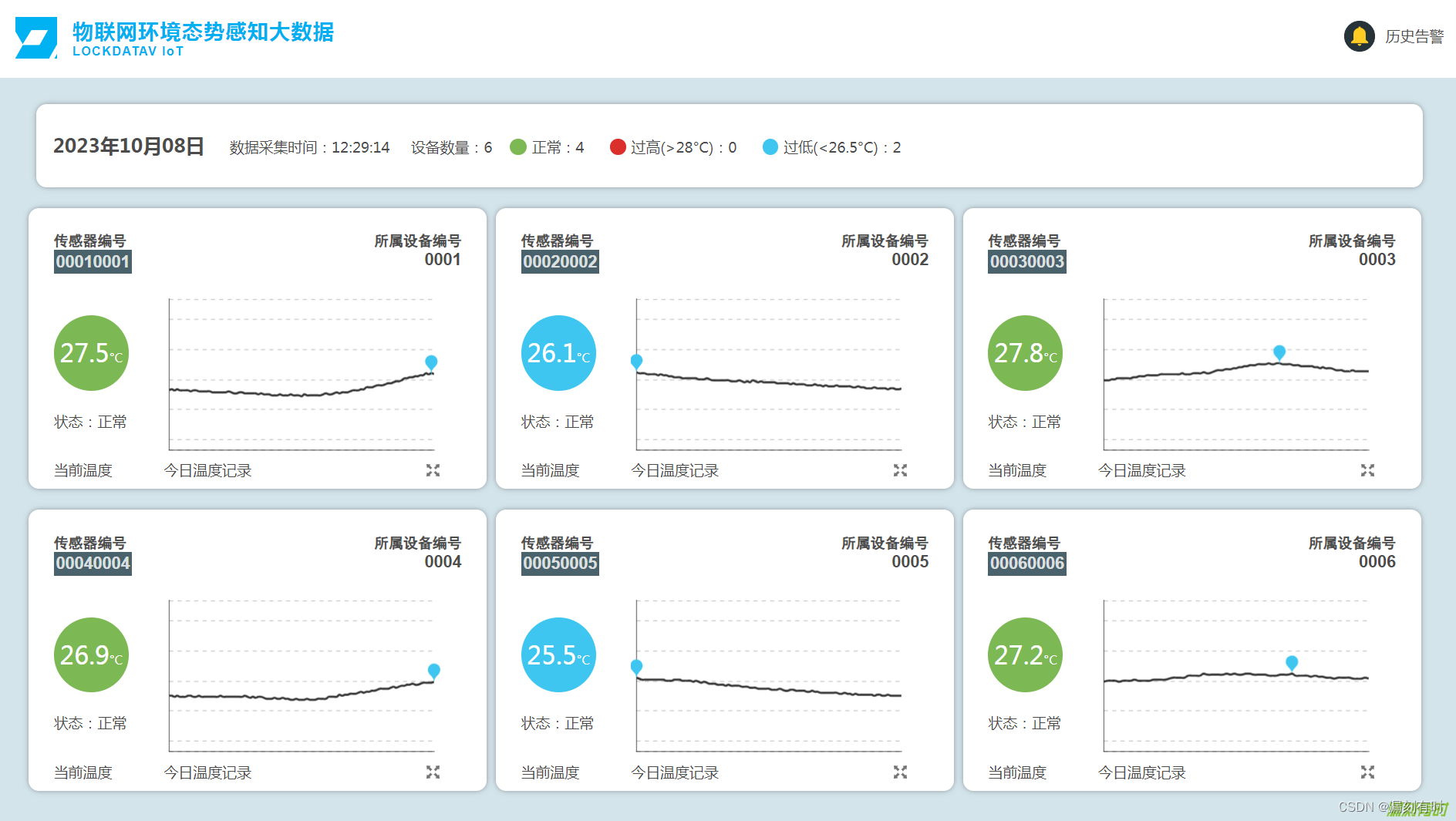
漏刻有时物联网环境态势感知大数据(设备列表、动态折线图)
物联网环境下的态势感知是指对物联网环境中的各种要素进行全面、实时、准确的监测、分析和预测,以实现网络态势的全面掌握和安全威胁的及时响应和处理。具体而言,态势感知以物联网环境为基础,利用各类传感器、数据采集设备和其他相关工具,对物联网设备、资产、数据流等进行…...

【力扣】单调栈:901. 股票价格跨度
【力扣】单调栈:901. 股票价格跨度 文章目录 【力扣】单调栈:901. 股票价格跨度1. 题目介绍2. 思路3. 解题代码参考 1. 题目介绍 设计一个算法收集某些股票的每日报价,并返回该股票当日价格的 跨度 。 当日股票价格的 跨度 被定义为股票价格…...

4_使用预训练模型 微调训练CIFAR10
使用预训练模型 微调训练CIFAR10 1. VGG 准备工作import torch from torch import nn import torchvision from torchvision import models from torchvision import datasets, transforms from datetime import datetime from tqdm import tqdm from torchsummary import sum…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...
:工厂方法模式、单例模式和生成器模式)
上位机开发过程中的设计模式体会(1):工厂方法模式、单例模式和生成器模式
简介 在我的 QT/C 开发工作中,合理运用设计模式极大地提高了代码的可维护性和可扩展性。本文将分享我在实际项目中应用的三种创造型模式:工厂方法模式、单例模式和生成器模式。 1. 工厂模式 (Factory Pattern) 应用场景 在我的 QT 项目中曾经有一个需…...

针对药品仓库的效期管理问题,如何利用WMS系统“破局”
案例: 某医药分销企业,主要经营各类药品的批发与零售。由于药品的特殊性,效期管理至关重要,但该企业一直面临效期问题的困扰。在未使用WMS系统之前,其药品入库、存储、出库等环节的效期管理主要依赖人工记录与检查。库…...

当下AI智能硬件方案浅谈
背景: 现在大模型出来以后,打破了常规的机械式的对话,人机对话变得更聪明一点。 对话用到的技术主要是实时音视频,简称为RTC。下游硬件厂商一般都不会去自己开发音视频技术,开发自己的大模型。商用方案多见为字节、百…...
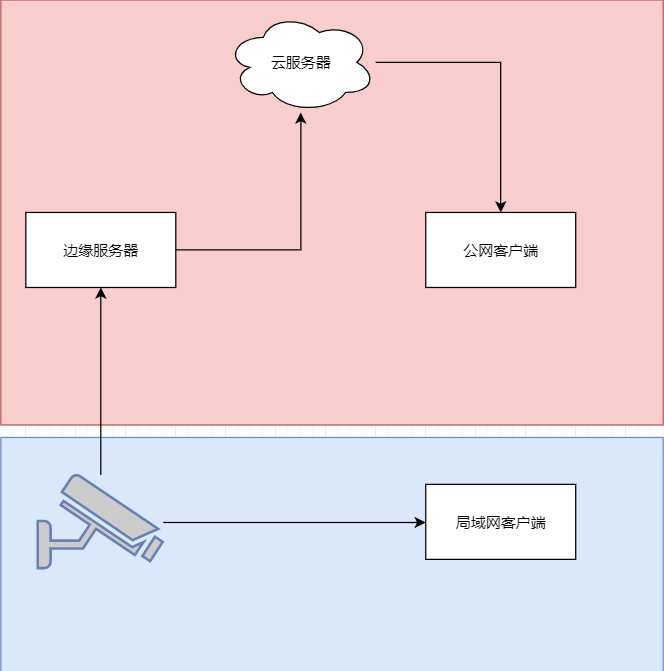
java 局域网 rtsp 取流 WebSocket 推送到前端显示 低延迟
众所周知 摄像头取流推流显示前端延迟大 传统方法是服务器取摄像头的rtsp流 然后客户端连服务器 中转多了,延迟一定不小。 假设相机没有专网 公网 1相机自带推流 直接推送到云服务器 然后客户端拉去 2相机只有rtsp ,边缘服务器拉流推送到云服务器 …...
