Leetcode---364场周赛
题目列表
2864. 最大二进制奇数
2865. 美丽塔 I
2866. 美丽塔 II
2867. 统计树中的合法路径数目
一、最大二进制奇数

这题只要你对二进制有了解(学编程的不会不了解二进制吧),应该问题不大,这题要求最大奇数,1.奇数:只要保证二进制的最低位上是1就行(这里为不了解二进制的同学解释一下,二进制从低位到高位的权重分别是2^0,2^1,2^2...即除了最低位其他位都是偶数,所以最低位必须是1)
2.最大:贪心,我们将除了最低位的1之外的所有1都往高位放,得到的数肯定是最大的
代码如下
class Solution {
public:string maximumOddBinaryNumber(string s) {int cnt1=count(s.begin(),s.end(),'1');return string(cnt1-1,'1')+string(s.size()-cnt1,'0')+'1';}
};二、美丽塔I

这题的数据范围比较小,可以直接暴力,将每一个元素都当成山顶算一遍最大高度,然后比较得到最大高度,代码如下
class Solution {
public:long long maximumSumOfHeights(vector<int>& maxHeights) {long long ans=0;int n=maxHeights.size();for(int i=0;i<n;i++){long long res=maxHeights[i];for(int j=i-1,Min=maxHeights[i];j>=0;j--){Min=min(Min,maxHeights[j]);res+=Min;}for(int j=i+1,Min=maxHeights[i];j<n;j++){Min=min(Min,maxHeights[j]);res+=Min;}ans=max(ans,res);}return ans;}
};三、美丽塔II
这题的题目和上一题一样,只是加大了数据范围,即不能用暴力枚举的方法解题,那么我们怎么优化算法呢?关键在于发现上面一题的算法中有什么是被重复计算的,我们只要减少这些无用的运算,就能实现算法的时间复杂度优化。
为了方便叙述,我将山顶前面的部分称为上坡,山顶后面的部分称为下坡,很显然,上面算法在每次计算上坡/下坡时,总是不断的遍历之前就已经遍历过的元素,那么我们如何根据已经遍历过的元素来求出当前的上坡/下坡的高度呢?而且上坡和下坡的计算是分开的互不影响的,只要我们提前处理出各种上坡和下坡的高度,我们就能在O(n)的时间里得到最大高度。
如何利用之前遍历的元素信息,得到当前的上坡/下坡的高度?以计算上坡为例,解析如下

代码如下
class Solution {
public:long long maximumSumOfHeights(vector<int>& maxHeights) {long long ans=0;int n=maxHeights.size();vector<long long>pre(n),suf(n);//分别代表以i为山顶的上坡和下坡stack<int>st;//里面存放下标,方便计算出栈个数和索引高度st.push(-1);//这里是为了方便计算,简化逻辑for(int i=0;i<n;i++){while(st.size()>1&&maxHeights[i]<maxHeights[st.top()])st.pop();int idx=st.top();pre[i]=(idx<0?0:pre[idx])+1LL*(i-st.top())*maxHeights[i];st.push(i);}st=stack<int>();//让栈为空st.push(n);//这里是为了方便计算,简化逻辑for(int i=n-1;i>=0;i--){while(st.size()>1&&maxHeights[i]<maxHeights[st.top()])st.pop();int idx=st.top();suf[i]=(idx==n?0:suf[idx])+1LL*(st.top()-i)*maxHeights[i];st.push(i);}for(int i=0;i<n;i++){ans=max(ans,pre[i]+suf[i]-maxHeights[i]);}return ans;}
};这里说明一下算法的时间复杂度为O(n),有人或许看到求pre/suf中有两层循环,就认为时间复杂度为O(n^2),但其实不是,我们来看一下while循环里面的出栈语句执行了多少次,因为我们入栈的元素是n个,所以出栈的元素也只能是n个,所以这条语句只能执行n次,所以时间复杂度为O(n)
四、统计树种的合法路径数量
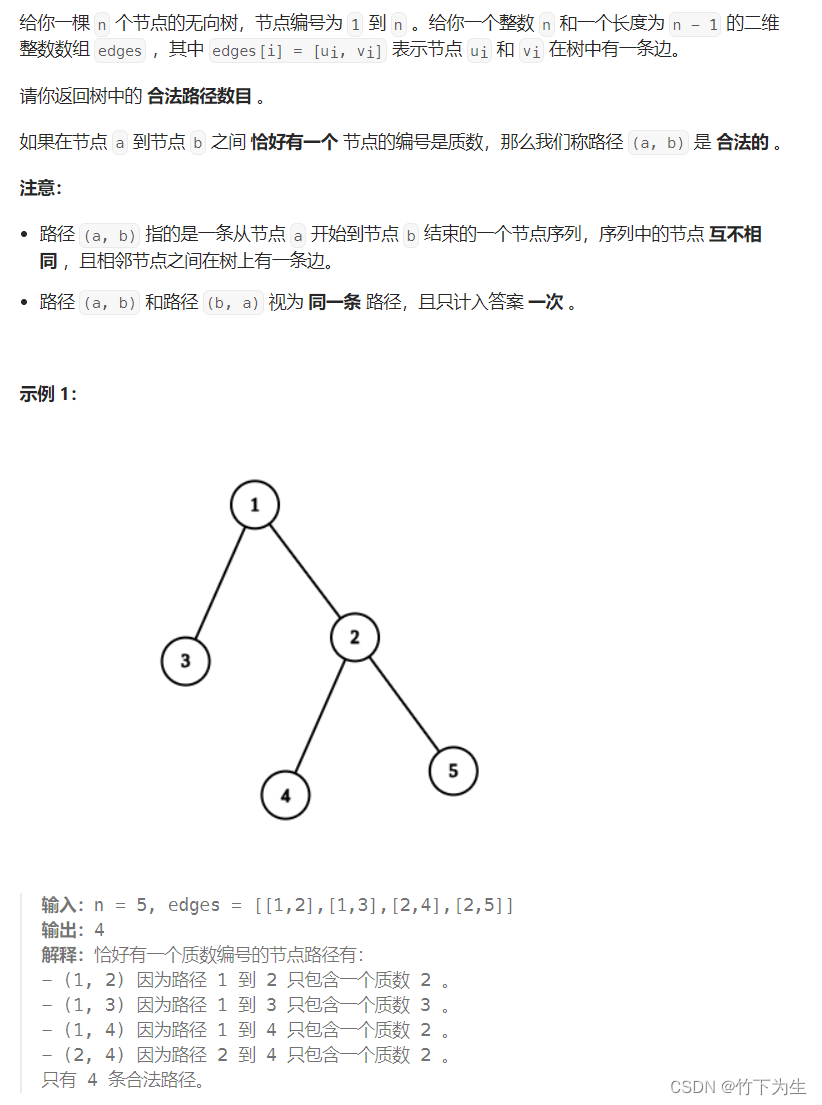
这题求路径个数,首先读懂题意,要求路径上包含一个质数,那么我们是从质数出发好,还是从非质数出发好呢?我们只要稍稍想一下就会发现从质数出发好,因为这样我们只要找到下一个质数就停止,而从非质数出发,我们就需要连续找到两个质数,很显然从非质数出发要处理的情况更多,所以我们从质数出发找路径,当然注意这题的路径至少需要两个结点(看示例一)
那么我们从质数出发怎么算呢?(判断质数就不讲了,不会的可以去看Leetcode-352周赛的第二题)
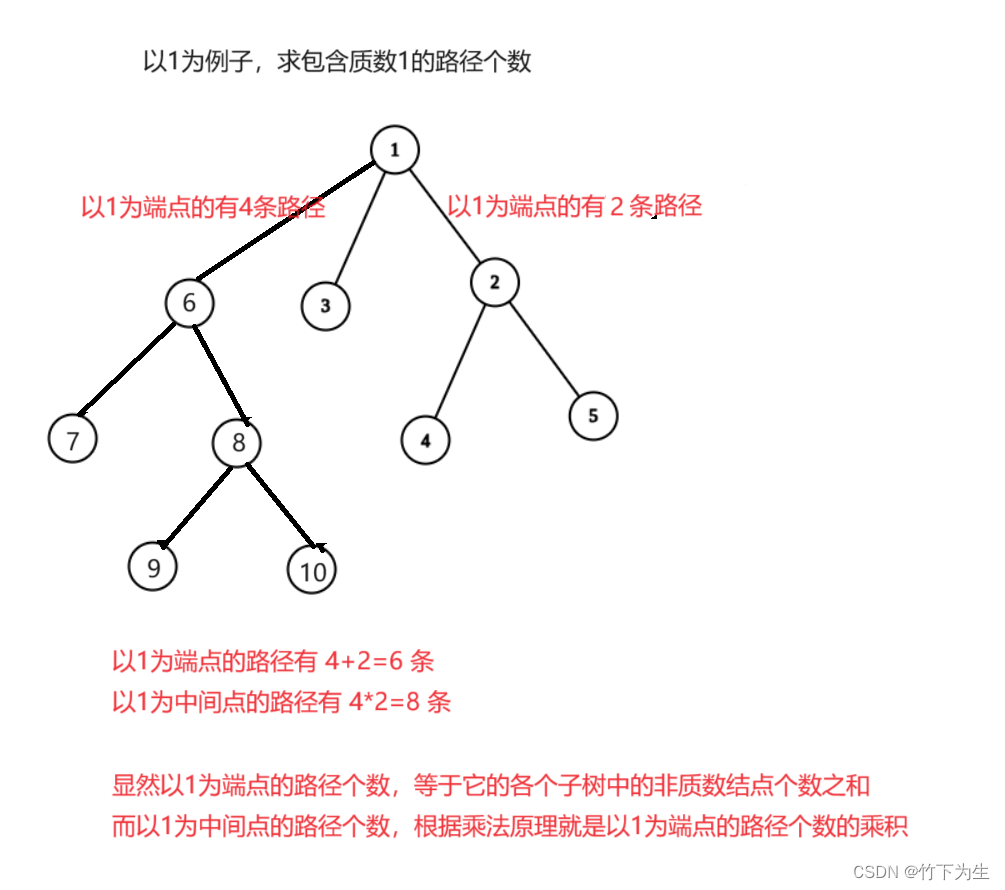
其他的路径求解方法同上,代码如下
//埃氏筛
const int MX=1e5;
vector<bool>is_prime(MX+1,true);
int init=[](){is_prime[1]=false;for(int i=2;i*i<=MX;i++){if(is_prime[i]){for(int j=i*i;j<=MX;j+=i){is_prime[j]=false;}}}return 0;
}();
class Solution {
public:long long countPaths(int n, vector<vector<int>>& edges) {vector<vector<int>>g(n+1);for(auto&e:edges){int x=e[0],y=e[1];g[x].push_back(y);g[y].push_back(x);}//计算质数结点连接的每一个子树中的非质数结点个数vector<int>sz(n+1);vector<int>nodes;function<void(int,int)> dfs=[&](int x,int fa){nodes.push_back(x);for(int y:g[x])if(y!=fa&&!is_prime[y])dfs(y,x);};long long ans=0;for(int x=1;x<=n;x++){if(!is_prime[x]) continue;int sum=0;for(int y:g[x]){if(is_prime[y]) continue;if(sz[y]==0){nodes.clear();dfs(y,-1);for(int z:nodes){sz[z]=nodes.size();}} ans+=(long long)sum*sz[y];//以i为中间点的路径sum+=sz[y];}ans+=sum;//以i为端点的路径}return ans;}
};相关文章:

Leetcode---364场周赛
题目列表 2864. 最大二进制奇数 2865. 美丽塔 I 2866. 美丽塔 II 2867. 统计树中的合法路径数目 一、最大二进制奇数 这题只要你对二进制有了解(学编程的不会不了解二进制吧),应该问题不大,这题要求最大奇数,1.奇数:只要保证…...

使用 Powershell 检索不理解的命令
使用 Powershell 检索不理解的命令 尝试使用 Powershell 完成 Powershell 的命令行 使用 Powershell 时,有时您会忘记某个 cmdlet 或想要了解哪些 cmdlet 可用。在这种情况下,最好在互联网上查找,但您也可以使用 Powershell 函数来完成。 以…...
基于 FPGA 的机器博弈五子棋游戏
基于 FPGA 的机器博弈五子棋游戏 一,设计目的 五子棋是一种深受大众喜爱的游戏,其规则简单,变化多端,非常富有趣味性 和消遣性。棋类游戏在具备娱乐性、益智性的同时也因为其载体大多是手机, 电脑等移动互联网设备导致现代社会低头族等现象更加严重,危害青少年的身 体健康…...
uCOSIII实时操作系统 三 移植
目录 uCOSIII简介: 准备工作: 准备基础工程: UCOSIII工程源码: UCOSIII移植: 向基础工程中添加相应的文件夹 向工程中添加分组 常见问题: 下载验证: uCOSIII简介: UCOS-I…...
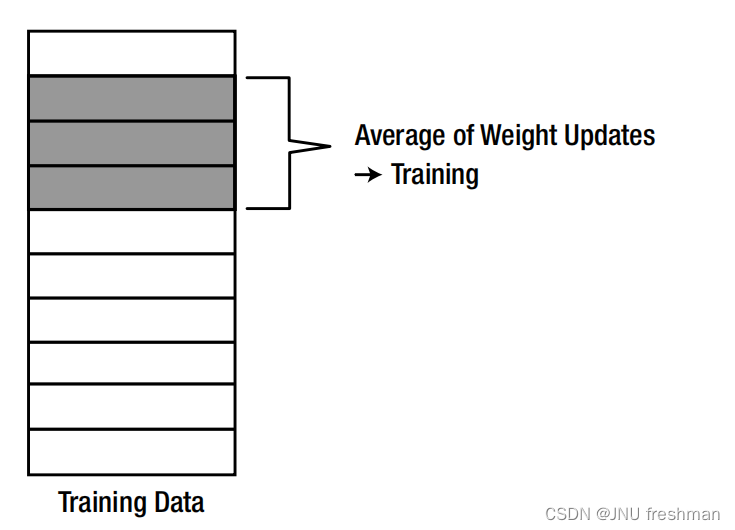
机器学习之SGD, Batch, and Mini Batch的简单介绍
文章目录 总述SGD(Stochastic Gradient Descent)(随机梯度下降)Batch (批量)mini Batch (迷你批量) 总述 SGD, Batch, and Mini Batch是可用于神经网络的监督学习计算权重更新的方案,即∆wij。 SGD(Stochastic Gradi…...

Windows电脑上的多开器与分布式存储系统的关系
Windows电脑上的多开器和分布式存储系统是两个不同的概念,二者之间没有直接的关系。 多开器是一种软件,它可以在Windows电脑上让用户同时运行多个同一应用程序的实例。多开器通常用于游戏玩家和应用程序测试人员等需要同时运行多个实例的用户。 分布式…...

积分球可以用于什么光谱光学检测
积分球是光测量的主要工具之一。积分球可以同时捕获一个光源发出的所有辐射。 1.光源测量 积分球可以用于测量光源的光通量、色温、光效等参数。通过将光源放置在积分球的入口处,球内的光线经过多次反射后形成均匀的照度分布,然后使用光度计或光谱仪对光…...

【力扣面试题】URL化
👑专栏内容:力扣刷题⛪个人主页:子夜的星的主页💕座右铭:前路未远,步履不停 目录 一、题目描述二、题目分析1、使用String内部方法2、使用StringBuilder 一、题目描述 题目链接:URL化 编写一种…...
计算机网络基础(二):物理层、数据链路层及网络层
一、物理层 1.物理层 物理层面的通信标准可以概括划分为与网络基础设施有关的标准和与被传输物理信号有关的标准两类。 网络基础设施的标准:鉴于物理层面的消息互通也是物理层应该兑现的服务,因此物理层的标准还会包括针脚的用途、线缆的材料与设计等…...

小白自学—网络安全(黑客技术)笔记
目录 一、自学网络安全学习的误区和陷阱 二、学习网络安全的一些前期准备 三、网络安全学习路线 四、学习资料的推荐 想自学网络安全(黑客技术)首先你得了解什么是网络安全!什么是黑客! 网络安全可以基于攻击和防御视角来分类…...
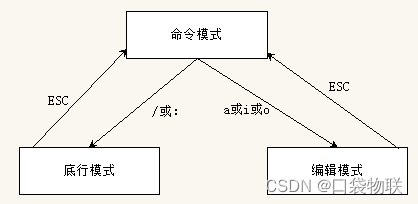
2.2.3 vim操作合集
1 vim VIM 是 Linux 系统上一款文本编辑器,学习 VIM 最好的文档,应该是阅读学习 VIM 的帮助文档,可以使用本地的帮助文件(vim--->:help),或者使用在线帮助文档。同时针对vim的使用,相应的相书籍也很多,如下 2 vim操作模式 命令模式:默认模式,该模式下可以移动光标…...
解决 Jenkins 性能缓慢的问题~转
解决 Jenkins 性能缓慢的问题 Docker中文社区 计算机技术与软件专业技术资格持证人 2 人赞同了该文章 没有什么比缓慢的持续集成系统更令人沮丧的了。它减慢了反馈循环并阻止代码快速投入生产。虽然像使用性能更好的服务器可以为您争取时间,但您最终必须投资…...

Matrix卡顿优化之IdleHandlerLagTracer源码分析
前言 IdleHandler是Android系统为开发者提供的一种在消息队列空闲时运行任务的机制,通过IdleHandler执行的任务优先级低于主线程优先级,会在主线程任务执行完成后再执行,所以适用于一些实时性要求不高的任务,通常用于Android启动…...
(ubuntu)Docker 安装linux 详情过程
文章目录 前言Docker 安装linux第一步:使用dokcker 拉取镜像:第二步:创建本地目录(用于挂载)第三步:(上传配置文件)修改配置文件第四步:创建docker容器第五步: 测试本地连…...
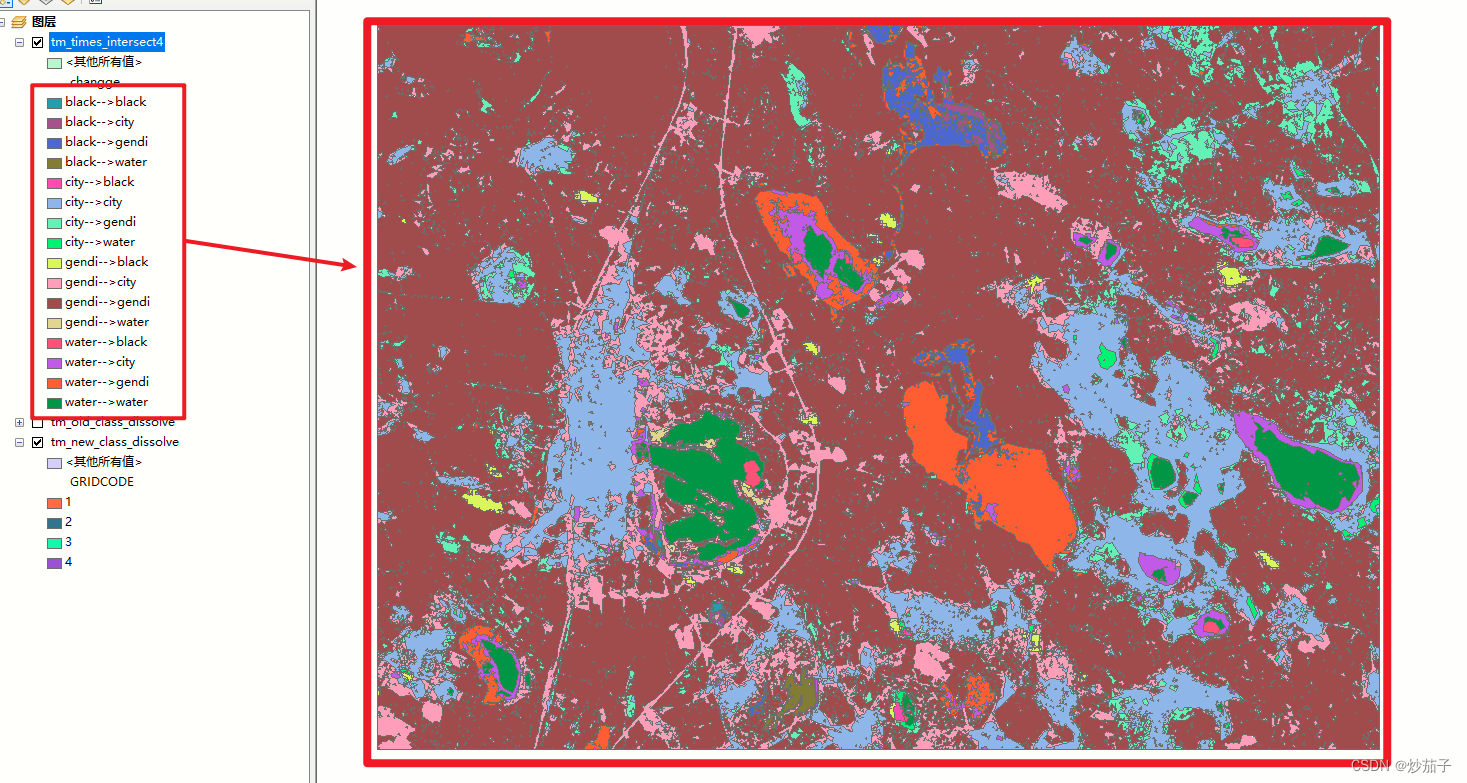
ArcMap:第二届全国大学生GIS技能大赛(广西师范学院)详解-上午题
目录 01 题目 1.1 第一小题 1.2 第二小题 1.3 第三小题 1.4 数据展示 02 思路和实操 2.1 第一问思路 2.2 第一问操作过程 2.2.1 地理配准 2.2.2 镶嵌 2.2.2.1 第一种镶嵌方法 2.2.2.2 第二种镶嵌方法 2.2.3 裁剪 2.2.4 DEM信息提取 2.2.5 分类 2.3 第二问思路 …...
Blender 导出 fbx 到虚幻引擎中丢失材质!!!(使用Blender导出内嵌材质的fbx即可解决)
目录 0 引言1 Blender导出内嵌纹理的fbx模型 0 引言 我在Blender处理了一些fbx模型后再次导出到UE中就经常出现,材质空白的情况(如下图所示),今天终于找到问题原因,记录下来,让大家避免踩坑。 其实原因很简…...

C++交换a和b的方法
以下是用C编写的交换a和b的六种方法: 1. 方法一:使用临时变量 #include <iostream>int main() {int a 5;int b 10;std::cout << "Before swapping: a " << a << ", b " << b << std::end…...
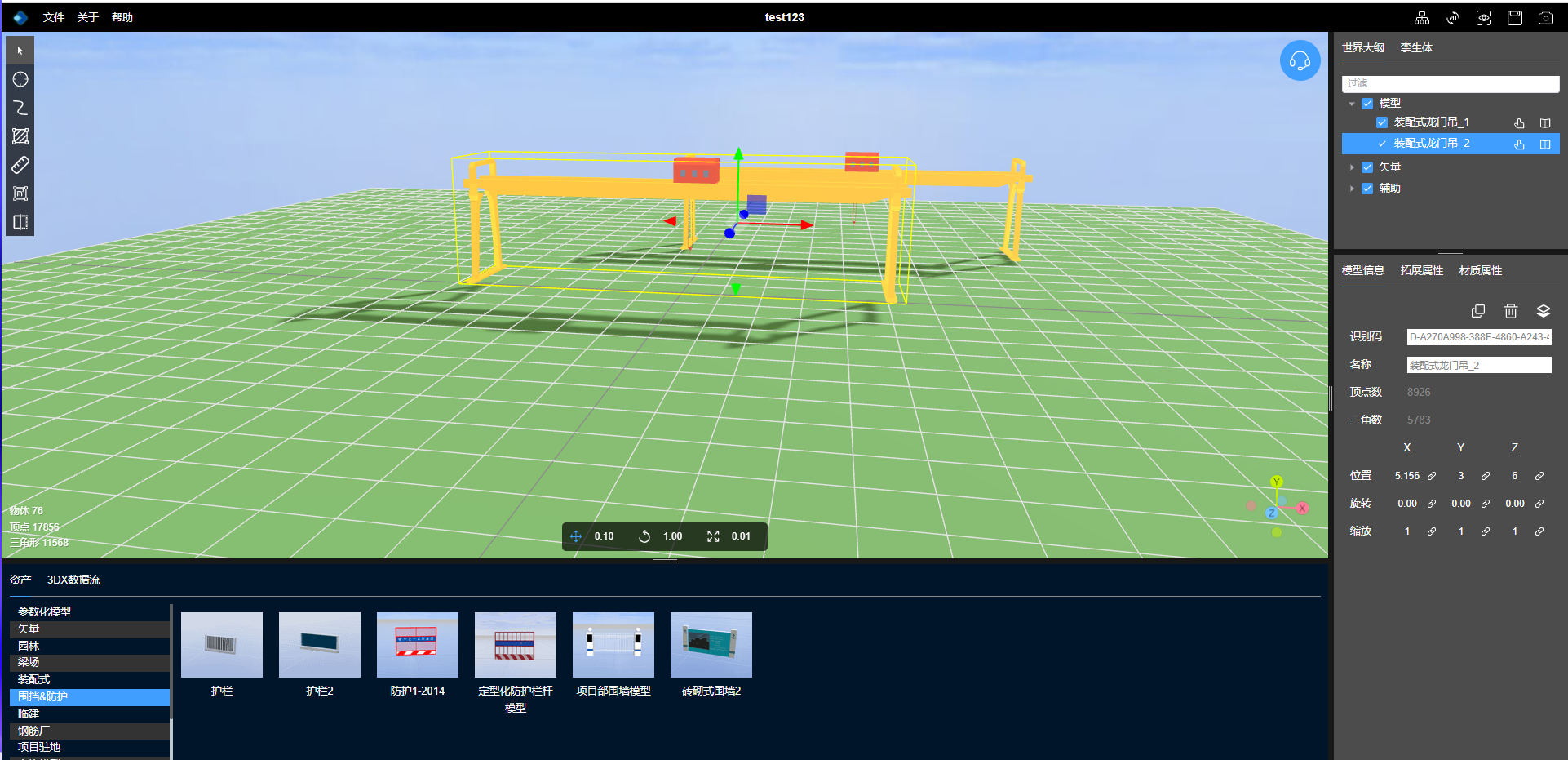
3D孪生场景搭建:模拟仿真
前面几期文章介绍如何使用NSDT 编辑器 搭建3D应用场景,本期介绍下孪生场景中一个一个非常重要的功能:模拟仿真。 1、什么是模拟仿真 模拟仿真是一种用于描述、分析和模拟现实世界中系统、过程或事件的计算机模型和程序。仿真通过输入各种参数和条件&am…...
美国各流域边界下载,并利用arcgis提取与处理
一、边界数据的下载 一般使用最普遍的流域边界数据是从HydroSHEDS官网下载: HydroBASINS代表一系列矢量多边形图层,以全球尺度呈现次级流域边界。该产品的目标是提供一种无缝的全球覆盖,其中包含了不同尺度(从数十到数百万平方千米…...
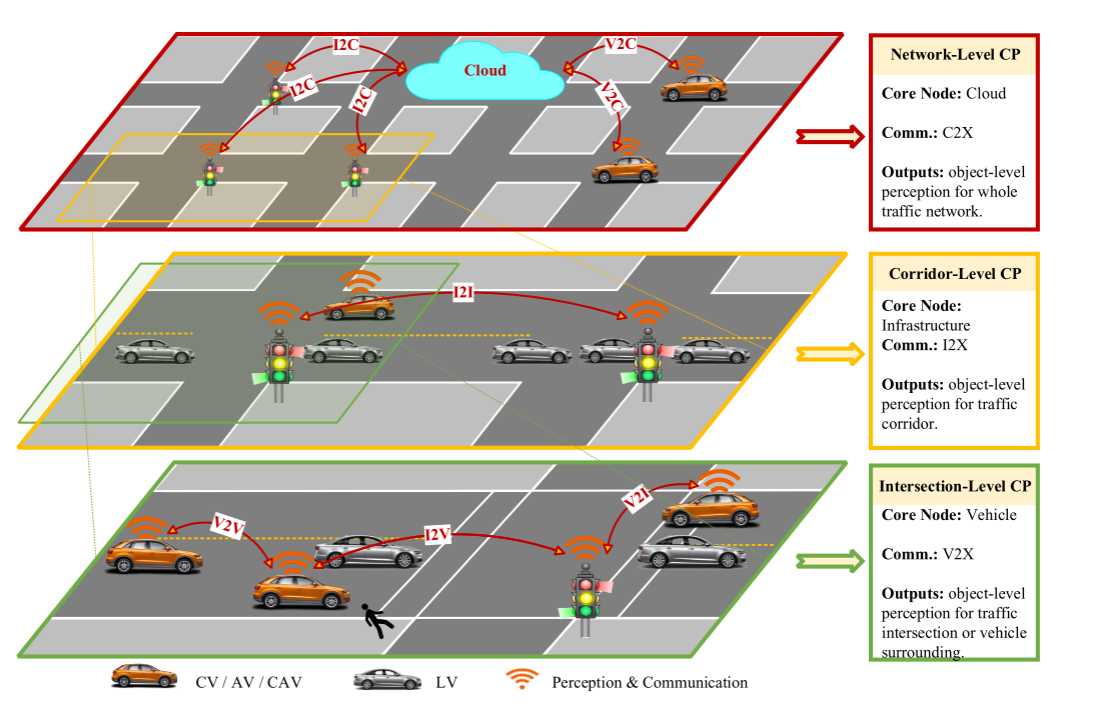
A Survey and Framework of Cooperative Perception 论文阅读
论文链接 A Survey and Framework of Cooperative Perception: From Heterogeneous Singleton to Hierarchical Cooperation 0. Abstract 首次提出统一的 CP(Cooperative Percepetion) 框架回顾了基于不同类型传感器的 CP 系统与分类对节点结构&#x…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...
