深度学习笔记之优化算法(四)Nesterov动量方法的简单认识
机器学习笔记之优化算法——Nesterov动量方法的简单认识
- 引言
- 回顾:梯度下降法与动量法
- Nesterov动量法
- Nesterov动量法的算法过程描述
- 总结
引言
上一节对动量法进行了简单认识,本节将介绍 Nesterov \text{Nesterov} Nesterov动量方法。
回顾:梯度下降法与动量法
关于梯度下降法的迭代步骤描述如下:
θ ⇐ θ − η ⋅ ∇ θ J ( θ ) \theta \Leftarrow \theta - \eta \cdot \nabla_{\theta} \mathcal J(\theta) θ⇐θ−η⋅∇θJ(θ)
以标准二次型 f ( x ) = x T Q x , Q = ( 0.5 0 0 20 ) , x = ( x 1 , x 2 ) T f(x) = x^T \mathcal Qx,\mathcal Q = \begin{pmatrix} 0.5 \quad 0 \\ 0 \quad 20 \end{pmatrix},x = (x_1,x_2)^T f(x)=xTQx,Q=(0.50020),x=(x1,x2)T为目标函数,使用梯度下降法求解目标函数 f ( x ) f(x) f(x)最小值的迭代过程如下:

很明显,由于 Q \mathcal Q Q的原因,导致在算法迭代过程中,迭代更新点对应的 Hessian Matrix ⇒ ∇ 2 f ( ⋅ ) \text{Hessian Matrix} \Rightarrow \nabla^2 f(\cdot) Hessian Matrix⇒∇2f(⋅)中的条件数都较大,从而使梯度下降法在该凸二次函数中的收敛速度沿着次线性收敛的方向退化,这也是图像中迭代路径震荡、折叠严重的主要原因。
这里仅观察少量几次迭代步骤,见下面局部图:

其中红色线表示梯度下降法在迭代过程中的更新方向;以第一次迭代的更新方向为例,将该方向进行分解,可以得到上述两个方向分量。
由于目标函数 f ( x ) f(x) f(x)中 x x x是一个二维向量,因而在上图中的蓝色箭头分别描述了该方向在 x 1 , x 2 x_1,x_2 x1,x2正交基上的分量。
从上述两个分量可以看出:
- 关于横轴分量,它一直指向前方,也就是最优解的方向;
- 而造成迭代过程震荡、折叠的是纵轴分量。
综上,从观察的角度描述迭代路径震荡折叠现象严重的原因在于:横轴上的分量向前跨越的步幅很小;相比之下,纵轴上的分量上下的波动很大。针对该现象,可以得到相应的优化思路:
具体效果见下图绿色实心箭头,其中第一步红色与绿色实线箭头重合,因为在初始化过程中通常将动量向量初始化为零向量导致,这里以第二次迭代为例进行描述。图中的红色虚线表示梯度下降法当前迭代步骤在横轴、纵轴上的分量;绿色虚线则表示优化思路在当前步骤在横轴、纵轴上的分量。
- 压缩纵轴分量上的波动幅度;
- 拉伸/延长横轴分量上的步幅,从而使其更快地达到极值点;

如何从数学角度达到这样的效果:利用过去迭代步骤中的梯度数据,对当前迭代步骤的梯度信息进行修正。继续观察第二次迭代步骤:

在第一次迭代步骤结束后,我们得到了一个历史梯度的分量信息,即图中的蓝色虚线;在执行第二次迭代步骤时,我们需要将该步骤的梯度分量与相应的历史梯度分量执行加权运算:
- 观察纵轴分量:由于历史纵轴分量与当前纵轴分量方向相反(红色、蓝色虚线垂直箭头),这势必会缩减当前迭代步骤的纵轴分量;
- 相反,观察横轴分量:历史横轴分量与当前横轴分量方向相同(红色、蓝色虚线横向箭头),这必然会扩张当前迭代步骤的横轴分量;
如何对历史梯度信息进行描述,我们需要引入一个新的变量 m m m,用于累积历史梯度信息:
{ m t = m t − 1 + ∇ θ ; t − 1 J ( θ t − 1 ) θ t = θ t − 1 − η ⋅ m t \begin{cases} m_{t} = m_{t-1} + \nabla_{\theta;t-1} \mathcal J(\theta_{t-1}) \\ \theta_t = \theta_{t-1} - \eta \cdot m_t \end{cases} {mt=mt−1+∇θ;t−1J(θt−1)θt=θt−1−η⋅mt
上式的 m t m_t mt确实达到了历史迭代步骤梯度累积的作用,但同样衍生出了新的问题:上面步骤仅是将历史梯度信息完整地存储进来,如果迭代步骤较多的情况下,由于历史信息在累积过程中没有任何的丢失,最终可能导致:迭代步骤较深时,初始迭代步骤的历史梯度信息对当前时刻梯度的更新没有参考价值。相反,有可能会给当前迭代步骤引向错误的方向。因而关于 m t m_t mt的调整方式表示如下:
{ m t = β ⋅ m t − 1 + ( 1 − β ) ⋅ ∇ θ ; t − 1 J ( θ t − 1 ) θ t = θ t − 1 − η ⋅ m t \begin{cases} m_t = \beta \cdot m_{t-1} + (1 - \beta) \cdot \nabla_{\theta;t-1} \mathcal J(\theta_{t-1}) \\ \theta_t = \theta_{t-1} - \eta \cdot m_t \end{cases} {mt=β⋅mt−1+(1−β)⋅∇θ;t−1J(θt−1)θt=θt−1−η⋅mt
关于上式的迭代加权运算被称作指数加权移动平均法。假设 β = 0.9 \beta = 0.9 β=0.9,关于 m t m_t mt的表示如下:
m t = 0.9 × m t − 1 + 0.1 × ∇ θ ; t − 1 J ( θ t − 1 ) = 0.9 × [ 0.9 × m t − 2 + 0.1 × ∇ θ ; t − 2 J ( θ t − 2 ) ] + 0.1 × ∇ θ ; t − 1 J ( θ t − 1 ) = ⋯ = 0.1 × 0. 9 0 × ∇ θ ; t − 1 J ( θ t − 1 ) + 0.1 × 0. 9 1 × ∇ θ ; t − 2 J ( θ t − 2 ) + 0.1 × 0. 9 2 × ∇ θ ; t − 3 J ( θ t − 3 ) + ⋯ + 0.1 × 0. 9 t − 1 × ∇ θ ; 1 J ( θ 1 ) \begin{aligned} m_t & = 0.9 \times m_{t-1} + 0.1 \times \nabla_{\theta;t-1} \mathcal J(\theta_{t-1}) \\ & = 0.9 \times \left[0.9 \times m_{t-2} + 0.1 \times \nabla_{\theta;t-2} \mathcal J(\theta_{t-2}) \right] + 0.1 \times \nabla_{\theta;t-1} \mathcal J(\theta_{t-1}) \\ & = \cdots \\ & = 0.1 \times 0.9^0 \times \nabla_{\theta;t-1} \mathcal J(\theta_{t-1}) + 0.1 \times 0.9^1 \times \nabla_{\theta;t-2} \mathcal J(\theta_{t-2}) + 0.1 \times 0.9^2 \times \nabla_{\theta;t-3} \mathcal J(\theta_{t-3}) + \cdots + 0.1 \times 0.9^{t-1} \times \nabla_{\theta;1} \mathcal J(\theta_1) \end{aligned} mt=0.9×mt−1+0.1×∇θ;t−1J(θt−1)=0.9×[0.9×mt−2+0.1×∇θ;t−2J(θt−2)]+0.1×∇θ;t−1J(θt−1)=⋯=0.1×0.90×∇θ;t−1J(θt−1)+0.1×0.91×∇θ;t−2J(θt−2)+0.1×0.92×∇θ;t−3J(θt−3)+⋯+0.1×0.9t−1×∇θ;1J(θ1)
很明显,距离当前迭代步骤越近的梯度,其保留权重越大;反之,随着迭代步骤的推移,越靠近初始迭代步骤的梯度权重越小。
这让我想起了 GRU \text{GRU} GRU神经网络~
这种方法就是动量法,也被称作冲量法。
Nesterov动量法
关于梯度下降法的优化,不仅可以像动量法一样考虑历史迭代步骤的梯度信息,实际上,我们同样可以超前参考未来的梯度信息。
关于动量法在某迭代步骤中的更新过程示例如下:

- 其中黄色结点表示动量法在迭代过程中的更新位置;淡蓝色曲线表示理想状态下的下降路径;
- 其中红色实线表示梯度下降法的更新方向;蓝色实线表示历史梯度构成的冲量信息;
很明显,当前迭代步骤的梯度方向与更新点处更高线的切线相垂直~
假设 β = 0.5 \beta = 0.5 β=0.5,图中的橘黄色虚线表示加权后真正的更新方向。我们不否认:此时动量法相比纯粹的梯度下降法,其下降路径更接近理想状态路径。两者比对效果如下:
很明显,梯度下降法不仅多使用一次迭代步骤,并且最后结果依然不及两步的动量法。

但即便动量法有更优的下降路径,但依然距离理想状态下的下降路径存在差距。
假设:在动量法执行完第一次迭代步骤前,就已经预估到了未来步骤的位置信息,那么通过未来步骤加权的第一次迭代的位置信息会进一步得到修正。从数学角度观察 Nesterov \text{Nesterov} Nesterov动量法是如何实现超前参考的。回顾动量法公式:
{ m t = β ⋅ m t − 1 + ( 1 − β ) ⋅ ∇ θ ; t − 1 J ( θ t − 1 ) θ t = θ t − 1 − η ⋅ m t \begin{cases} m_t = \beta \cdot m_{t-1} + (1 - \beta) \cdot \nabla_{\theta;t-1} \mathcal J(\theta_{t-1}) \\ \theta_t = \theta_{t-1} - \eta \cdot m_t \end{cases} {mt=β⋅mt−1+(1−β)⋅∇θ;t−1J(θt−1)θt=θt−1−η⋅mt
其中 ∇ θ ; t − 1 J ( θ t − 1 ) \nabla_{\theta;t-1} \mathcal J(\theta_{t-1}) ∇θ;t−1J(θt−1)表示当前迭代步骤 t t t的梯度信息;而 Nesterov \text{Nesterov} Nesterov动量法是将上一迭代步骤的 θ t − 1 ⇐ θ t − 1 + γ ⋅ m t − 1 \theta_{t-1} \Leftarrow \theta_{t- 1} + \gamma \cdot m_{t-1} θt−1⇐θt−1+γ⋅mt−1,从而得到一个新时刻的未知的权重信息,并使用该信息替换 θ t − 1 \theta_{t-1} θt−1参与运算:
之所以是新时刻,或者说是未来时刻,是因为当前迭代步骤的 θ t \theta_t θt还没有被解出来,而 θ t − 1 + γ ⋅ m t − 1 \theta_{t-1} + \gamma \cdot m_{t-1} θt−1+γ⋅mt−1又确实是超越了 t − 1 t-1 t−1迭代步骤的新信息。
{ m t = β ⋅ m t − 1 + ( 1 − β ) ⋅ ∇ θ ; t − 1 J ( θ t − 1 + γ ⋅ m t − 1 ) θ t = θ t − 1 − η ⋅ m t \begin{cases} m_t = \beta \cdot m_{t-1} + (1 - \beta) \cdot \nabla_{\theta;t-1} \mathcal J(\theta_{t-1} + \gamma \cdot m_{t-1}) \\ \theta_t = \theta_{t-1} - \eta \cdot m_t \end{cases} {mt=β⋅mt−1+(1−β)⋅∇θ;t−1J(θt−1+γ⋅mt−1)θt=θt−1−η⋅mt
继续观察上式:关于超前信息 θ t − 1 + γ ⋅ m t − 1 \theta_{t-1} + \gamma \cdot m_{t-1} θt−1+γ⋅mt−1,它的格式与 θ t = θ t − 1 − η ⋅ m t \theta_t = \theta_{t-1} - \eta \cdot m_{t} θt=θt−1−η⋅mt非常相似,相当于该超前信息是 θ t − 1 \theta_{t-1} θt−1与 m t − 1 m_{t-1} mt−1之间的加权方向。
为简化起见,这里仅描述一步: t − 1 ⇒ t t-1 \Rightarrow t t−1⇒t
- 初始状态下,下图描述的是动量法的一次迭代步骤;红色实线表示 ∇ θ ; t − 1 ∇ J ( θ t − 1 ) \nabla_{\theta;t-1} \nabla \mathcal J(\theta_{t-1}) ∇θ;t−1∇J(θt−1);蓝色实线表示 m t − 1 m_{t-1} mt−1,中间的橙黄色虚线表示两者的加权结果 m t = β ⋅ m t − 1 + ( 1 − β ) ⋅ ∇ θ ; t − 1 J ( θ t − 1 ) m_t = \beta \cdot m_{t-1} + (1 - \beta) \cdot \nabla_{\theta;t-1} \mathcal J(\theta_{t-1}) mt=β⋅mt−1+(1−β)⋅∇θ;t−1J(θt−1)

- 那么超前信息 θ t − 1 + γ ⋅ m t − 1 \theta_{t-1} + \gamma \cdot m_{t-1} θt−1+γ⋅mt−1如何表示 ? ? ?假设图中 θ t − 1 \theta_{t-1} θt−1到红色点的长度为 γ ⋅ m t − 1 \gamma \cdot m_{t-1} γ⋅mt−1,那么红色点的位置就是超前信息的位置:

- 至此,可以描述 ∇ θ ; t − 1 J ( θ t − 1 + γ ⋅ m t − 1 ) \nabla_{\theta;t-1} \mathcal J(\theta_{t-1} + \gamma \cdot m_{t-1}) ∇θ;t−1J(θt−1+γ⋅mt−1)的方向:过红色点,与目标函数等高线相垂直的方向。
图中的红色虚线表示∇ θ ; t − 1 J ( θ t − 1 + γ ⋅ m t − 1 ) \nabla_{\theta;t-1} \mathcal J(\theta_{t-1} + \gamma \cdot m_{t-1}) ∇θ;t−1J(θt−1+γ⋅mt−1)的方向,仔细观察可以发现,它与∇ θ ; t − 1 J ( θ t − 1 ) \nabla_{\theta;t-1} \mathcal J(\theta_{t-1}) ∇θ;t−1J(θt−1)描述的红色实线之间存在一丢丢的偏移,不是平行的~

- 接下来,将红色虚线替代红色实线,并得到 Nesterov \text{Nesterov} Nesterov动量法中的 m t = β ⋅ m t − 1 + ( 1 − β ) ⋅ ∇ θ ; t − 1 J ( θ t − 1 + γ ⋅ m t − 1 ) m_{t} = \beta \cdot m_{t-1} + (1 - \beta) \cdot \nabla_{\theta;t-1} \mathcal J(\theta_{t-1} + \gamma \cdot m_{t-1}) mt=β⋅mt−1+(1−β)⋅∇θ;t−1J(θt−1+γ⋅mt−1):
橙黄色虚线指向的红色点表示Nesterov \text{Nesterov} Nesterov动量法中的经过η \eta η修饰的m t m_t mt结果(这里暂定η \eta η不变的情况下),我们仍可以看出,相比于动量法, Nesterov \text{Nesterov} Nesterov动量法在迭代过程中能够更偏向理想状态下降路径。

Nesterov动量法的算法过程描述
基于 Nesterov \text{Nesterov} Nesterov动量法的随机梯度下降的算法步骤表示如下:
初始化操作:
- 学习率 η \eta η,动量因子 γ \gamma γ;
- 初始化参数 θ \theta θ,初始动量 m m m;
算法过程:
- While \text{While} While没有达到停止准则 do \text{do} do
- 从训练集 D \mathcal D D中采集出包含 k k k个样本的小批量: { ( x ( i ) , y ( i ) ) } i = 1 k \{(x^{(i)},y^{(i)})\}_{i=1}^k {(x(i),y(i))}i=1k;
- 应用临时的超前参数 θ ^ \hat \theta θ^:
θ ^ ⇐ θ + γ ⋅ m \hat \theta \Leftarrow \theta + \gamma \cdot m θ^⇐θ+γ⋅m - 使用超前参数 θ ^ \hat \theta θ^计算该位置的梯度信息:
G ⇐ 1 k ∑ i = 1 k ∇ θ L [ f ( x ( i ) ; θ ^ ) , y ( i ) ] \mathcal G \Leftarrow \frac{1}{k} \sum_{i=1}^k \nabla_{\theta} \mathcal L[f(x^{(i)};\hat \theta),y^{(i)}] G⇐k1i=1∑k∇θL[f(x(i);θ^),y(i)] - 计算动量更新:
m ⇐ γ ⋅ m − η ⋅ G m \Leftarrow \gamma \cdot m - \eta \cdot \mathcal G m⇐γ⋅m−η⋅G - 计算参数 θ \theta θ更新:
θ ⇐ θ + m \theta \Leftarrow \theta + m θ⇐θ+m - End While \text{End While} End While
总结
观察上述算法过程,可以发现:虽然我们更新的是 θ \theta θ,但整个算法至始至终都没有求解 θ \theta θ的梯度: ∇ θ J ( θ ) \nabla_{\theta} \mathcal J(\theta) ∇θJ(θ),也就是说: m m m中的历史信息也均是超前梯度 ∇ θ J ( θ + γ ⋅ m ) \nabla_{\theta} \mathcal J(\theta + \gamma \cdot m) ∇θJ(θ+γ⋅m)构成的历史信息。
Reference \text{Reference} Reference:
“随机梯度下降、牛顿法、动量法、Nesterov、AdaGrad、RMSprop、Adam”,打包理解对梯度下降的优化
深度学习(花书) P182 8.3.2 \text{P182 8.3.2} P182 8.3.2动量; 8.3.3 nesterov \text{8.3.3 nesterov} 8.3.3 nesterov动量
相关文章:

深度学习笔记之优化算法(四)Nesterov动量方法的简单认识
机器学习笔记之优化算法——Nesterov动量方法的简单认识 引言回顾:梯度下降法与动量法Nesterov动量法Nesterov动量法的算法过程描述总结 引言 上一节对动量法进行了简单认识,本节将介绍 Nesterov \text{Nesterov} Nesterov动量方法。 回顾:…...

比 N 小的最大质数
系列文章目录 进阶的卡莎C++_睡觉觉觉得的博客-CSDN博客数1的个数_睡觉觉觉得的博客-CSDN博客双精度浮点数的输入输出_睡觉觉觉得的博客-CSDN博客足球联赛积分_睡觉觉觉得的博客-CSDN博客大减价(一级)_睡觉觉觉得的博客-CSDN博客小写字母的判断_睡觉觉觉得的博客-CSDN博客纸币(…...

JavaScript 生成随机颜色
代码 function color(color) {return (color "0123456789abcdef"[Math.floor(Math.random() * 6)]) && (color.length 6 ? color : arguments.callee(color)); }使用 // 用法1:全部随机生成 "#" color(""); // #201050…...

Savepoints
语法 SAVEPOINT 名称 RELEASE SAVEPOINT 名称 ROLLBACK TRANSACTION TO SAVEPOINT 名称 Savepoints 与BEGIN和COMMIT类似的创建事务的方法,名称不要求唯一且可以嵌套使用。 可以用在BEGIN…COMMIT定义的事务内部或外部。当在外部时,最外层的savepoin…...

【MySQL】基本查询(二)
文章目录 一. 结果排序二. 筛选分页结果三. Update四. Delete五. 截断表六. 插入查询结果结束语 操作如下表 //创建表结构 mysql> create table exam_result(-> id int unsigned primary key auto_increment,-> name varchar(20) not null comment 同学姓名,-> chi…...
Qt:多语言支持,构建全面应用程序“
Qt:强大API、简化框架、多语言支持,构建全面应用程序" 强大的API:Qt提供了丰富的API,包括250多个C类,基于模板的集合、序列化、文件操作、IO设备、目录管理、日期/时间等功能。还包括正则表达式处理和支持2D/3D…...
性能监控-链路级监控工具
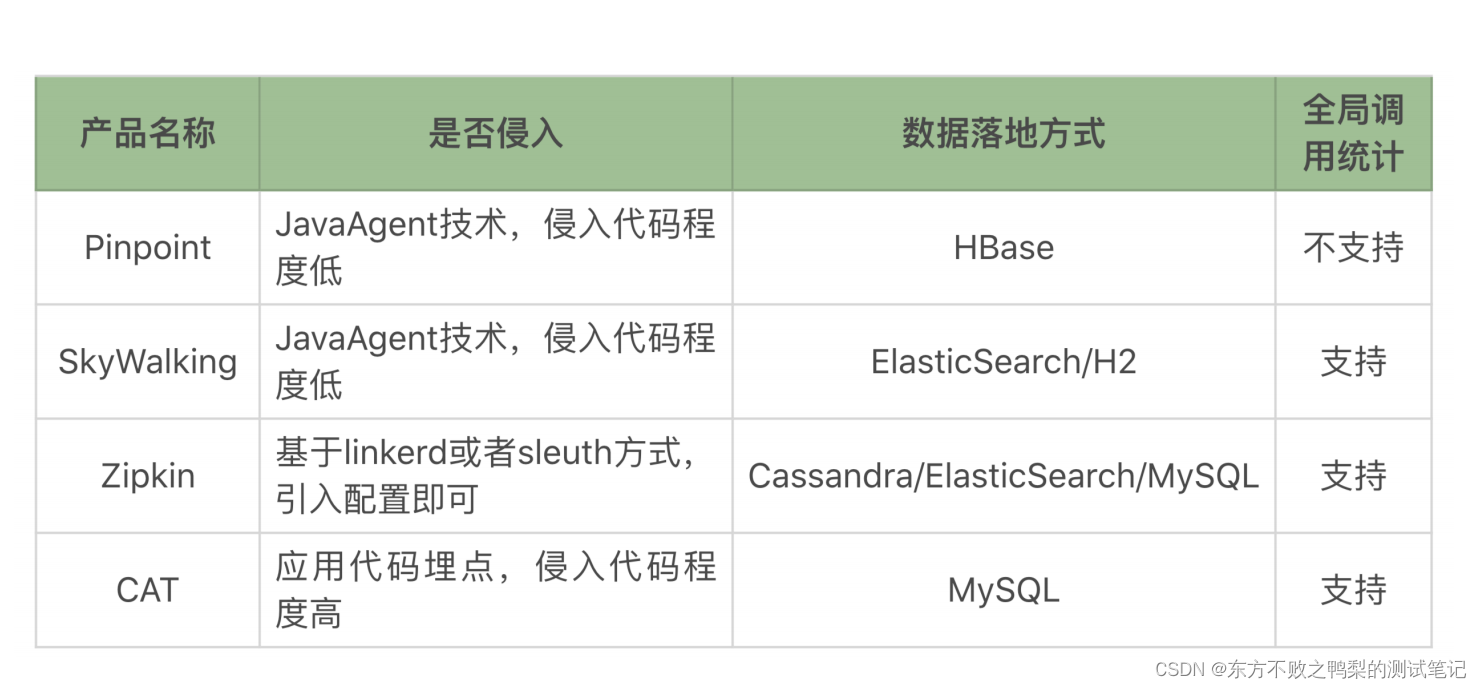
常见的链路监控工具,我们都称之为 APM 开源工具 几个开源的好用的工具,它们分别是 Pinpoint、SkyWalking、Zipkin、CAT 网络上也有人对这几个工具做过测试 比对,得到的结论是每个产品对性能的影响都在 10% 以下,其中 SkyWalking …...

clickonce 程序发布到ftp在使用cnd 加速https 支持下载,会不会报错
ClickOnce 是一种用于发布和部署.NET应用程序的技术,通常用于本地部署或通过网络分发应用程序。将 ClickOnce 程序发布到 FTP 服务器并使用 CDN(内容分发网络)进行加速是可能的,但要确保配置正确以避免出现错误。 在使用 CDN 加速…...
Nginx详细学习记录
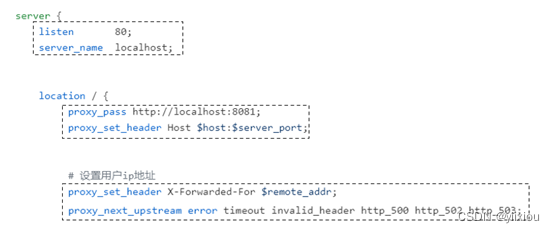
1. Nginx概述 Nginx是一个轻量级的高性能HTTP反向代理服务器,同时它也是一个通用类型的代理服务器,支持绝大部分协议,如TCP、UDP、SMTP、HTTPS等。 1.1 Nginx基础架构 Nginx默认采用多进程工作方式,Nginx启动后,会运行…...
golang gin——中间件编程以及jwt认证和跨域配置中间件案例
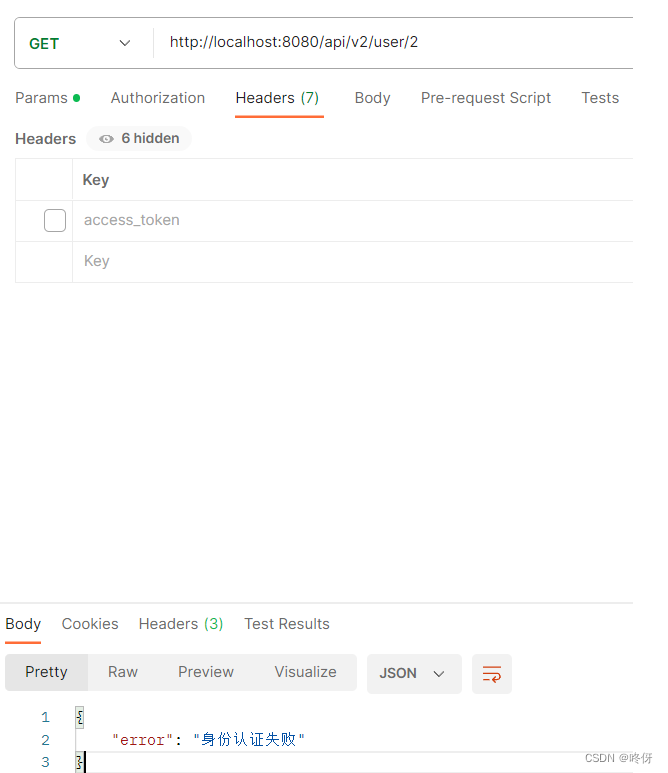
中间件编程jwt认证 在不改变原有方法的基础上,添加自己的业务逻辑。相当于grpc中的拦截器一样,在不改变grpc请求的同时,插入自己的业务。 简单例子 func Sum(a, b int) int {return a b }func LoggerMiddleware(in func(a, b int) int) f…...
如何快速制作令人惊叹的长图海报
在当今的数字时代,制作一张吸引人的长图海报已成为许多人的需求。无论是为了宣传活动,还是展示产品,一张设计精美的长图海报都能引起人们的注意。下面,我们将介绍一种简单的方法,使用在线海报制作工具来创建长图海报。…...
 : DS循环链表—约瑟夫环(Ver. I - A))
D (1092) : DS循环链表—约瑟夫环(Ver. I - A)
Description N个人坐成一个圆环(编号为1 - N),从第S个人开始报数,数到K的人出列,后面的人重新从1开始报数。依次输出出列人的编号。 例如:N 3,K 2,S 1。 2号先出列,然…...

Python爬虫(二十二)_selenium案例:模拟登陆豆瓣
本篇博客主要用于介绍如何使用seleniumphantomJS模拟登陆豆瓣,没有考虑验证码的问题,更多内容,请参考:Python学习指南 #-*- coding:utf-8 -*-from selenium import webdriver from selenium.webdriver.common.keys import Keysimp…...
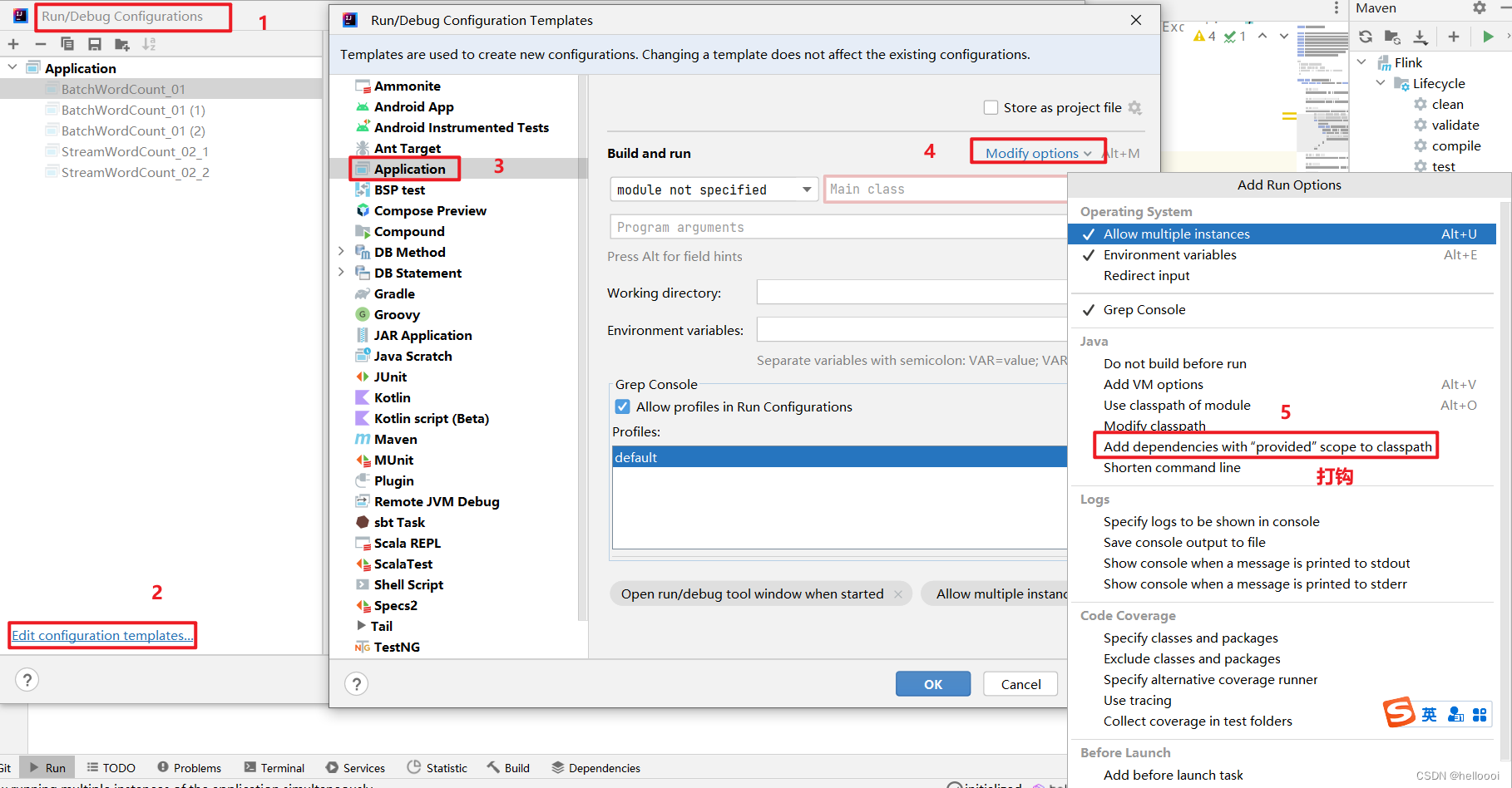
1. Flink程序打Jar包
文章目录 步骤注意事项 步骤 用 maven 打 jar 包,需要在 pom.xml 文件中添加打包插件依赖 <build><plugins><plugin><groupId>org.apache.maven.plugins</groupId><artifactId>maven-shade-plugin</artifactId><ver…...

水波纹文字效果动画
效果展示 CSS 知识点 text-shadow 属性绘制立体文字clip-path 属性来绘制水波纹 工具网站 CSS clip-path maker 效果编辑器 页面整体结构实现 使用多个 H2 标签来实现水波纹的效果实现,然后使用clip-path结合动画属性一起来进行波浪的起伏动画实现。 <div …...

【1.1】神经网络:关于神经网络的介绍
✅作者简介:大家好,我是 Meteors., 向往着更加简洁高效的代码写法与编程方式,持续分享Java技术内容。 🍎个人主页:Meteors.的博客 💞当前专栏: 神经网络(随缘更新) ✨特色…...
java项目中git的.ignore文件设置
在Git中,ignore是用来指定Git应该忽略的故意不被追踪的文件。它并不影响已经被Git追踪的文件。我们可以通过.ignore文件在Git中指定要忽略的文件。 当我们执行git add命令时,Git会检查.gitignore文件,并自动忽略这些文件和目录。这样可以避免…...

11.3 读图举例
一、低频功率放大电路 图11.3.1所示为实用低频功率放大电路,最大输出功率为 7 W 7\,\textrm W 7W。其中 A \textrm A A 的型号为 LF356N, T 1 T_1 T1 和 T 3 T_3 T3 的型号为 2SC1815, T 4 T_4 T4 的型号为 2SD525, T 2…...

黑马JVM总结(二十八)
(1)语法糖-foreach (2)语法糖-switch-string (3)语法糖-switch-enum (4)语法糖-枚举类 枚举类 (5)语法糖-twr1...

2023年DDoS攻击发展趋势的分析和推断
DDoS是一种非常“古老”的网络攻击技术,随着近年来地缘政治冲突对数字经济格局的影响,DDoS攻击数量不断创下新高,其攻击的规模也越来越大。日前,安全网站Latest Hacking News根据DDoS攻击防护服务商Link11的统计数据,对…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...
