C位操作符
目录
一、位操作符
1.位与&
2.位或|
3.位取反~
4.位异或^
5.位与,位或,位异或的特点总结
6.左移位《《 右移位 》》
二、位与,位或,位异或在操作寄存器时的特殊作用
1.寄存器操作的要求(特定位改变而不影响其他位)
2.特定位清零用&
3.特定位置1用|
4.特定位取反用^
三、用位运算构建特定二进制数
1.寄存器位操作经常需要特定位给特定值
2.使用位移获取特定位为1的二进制数
3.再结合位取反获取特定位为0的二进制数
4.总结:
四、位运算实战
1.例题1
2.例题2
3.例题3
4.例题4
5.例题5
6.例题6
7.例题7
8.例题8
方法1:
方法2:
五、用宏定义完成位运算
1.直接用宏来置位【赋1】,复位【赋0】(最右边为第1位)
1.1
1.2
1.3
2.截取遍历的部分连续位
一、位操作符
1.位与&
(1)位与符号是一个&,两个&&是逻辑与
(2)真值表:1&0=0 1&1=1 0&0=0 0&1=0
(3)从真值表可以看出:位与操作的特点是,只有1和1位于结果为1,其余全是0
(4)位于和逻辑与的区别:位与时两个操作数是按照二进制位批次对应位相与的,
逻辑与是两个操作数作为整体来相与的(举例:0xAA&0xF0=0xA0 ,0xAA && 0xF0=1)
2.位或|
(1)位或符号是一个|,两个||是逻辑或
(2)真值表;1|0=1 1|1=1 0|0=0 0|1=1
(3)从真值表可以看出:位或时两个操作数是按照二进制彼此对应位相与的,
逻辑或是两个操作数作为整体来相或的。
3.位取反~
(1)C语言中位取反是~,C语言中的逻辑取反是!
(2)按位取反是将操作数的二进制位逐个按位取反(1变成0,0变成1)
逻辑取反是真(在C语言中只要不是0的任何数都是真)变成假(在C语言中只有0表示假),假变成真。
#include<stdio.h>
int main() {int a = 45;int b, c;b = ~a; //按位取反,逐个位操作,1变0,0变1c = !a; //按逻辑取反【整体改变】,真变假,假变真printf("b=%d\n", b);//-64printf("c=%d\n", c);//0}#include<stdio.h>
int main() {int a = 45;int b, c;b = ~(~a); //等价于~~ac = !(!a); //等价于!!aprintf("b=%d\n", b);//45printf("c=%d\n", c);//1}实验;
任何非0的数被按逻辑取反再取反就会得到1
任何非0的数被按位取反再取反就会得到它自己
4.位异或^
(1)异或真值表:1^1=0 0^0=0 1^0=1 0^1=1(记忆方法:2个数如果相等结果为0,不等结果为1)
//45:0010 1101//^//23:0001 0111//= 0011 1010=58unsigned int a = 45, b = 23;unsigned int c;c = a ^ b;//58printf("c=%d\n", c);5.位与,位或,位异或的特点总结
位与:(任何数,其实就是1和0)与1位与无变化,与0位于变成0
位或:(任何数,其实就是1和0)与1位或变成1,与0位或无变化
位异或:(任何数,其实就是1和0)与1位异或会取反,与0位异或无变化
6.左移位《《 右移位 》》
C语言的位移要取决于数据类型
对于无符号数,左移动时右侧补0(相当于逻辑移位)
对于无符号数,右移动左侧补0(相当于逻辑移位)
对于有符号数。左移时候右侧补0(角算术移位,相当于逻辑移位)
对于有符号数,右移动时候左侧补符号位(如果整数就0,负数就补1,叫算术移位)
二、位与,位或,位异或在操作寄存器时的特殊作用
1.寄存器操作的要求(特定位改变而不影响其他位)
(1)ARM是内存与IO统一编址的,ARM中有很多内部外设,SoC中的CPU通过向这些内部外设的寄存器写入一些特定的值来操控逐个内部外设,进而操控硬件动作。所以可以说,读写寄存器就是操控硬件
(2)寄存器的特定是按位进行规划和使用。但是寄存器的读写却是整体32位一起进行的。(也就是说你只想修改
(3)寄存器操作要求是:在设定特定位时不能影响其他位。
(4)如何做到?答案是:读-改-写(三部曲)。读改写的操作理念,就是:当我想改变一个寄存器中某些特定位时,我不会直接去给他写,我会先读出寄存器整体原来的值,然后再逐个基础上修改我想要修改的特定位,再将修改后的值整体写入寄存器。这样达到的效果是:再不影响其他位原来值的情况下,我关心的位的值硬件被修改了。
2.特定位清零用&
位与:(任何数,其实就是1和0)与1位与无变化,与0位于变成0
(2)如果希望将一个寄存器的某些特定位变成0而不影响其他位,可以构造一个合适的1和0组成的数和这个寄存器原来的值进行位与操作,就可以将特定位清零
(3)假设原来32位寄存器中的值为:0xaaaa aaaa,我们希望将bit8-bit15清零而其他位不变,可以将这个数与0xffff 00ff进行位与即可【想要变成0的位直接写上0,其他位写1即可】
#include<stdio.h>
int main() {unsigned int a = 0xaaaaaaaa;unsigned int b = 0xffffffff;unsigned int c;//将想要变成0的位置写上0,其他位写上1c = a & b;printf("c=0x%x\n", c);//0xaaaaaaaa
}3.特定位置1用|
位或:(任何数,其实就是1和0)与1位或变成1,与0位或无变化
(2)要置1的位写上1,其他位为0,然后将这个数与相关的数进行位或
//位或:特定位置1用|//把寄存器值的bit4-bit7置1,其他位不变unsigned int a = 0x123d0c57;unsigned int b = 0xf0;unsigned int c;c = a | b;printf("c=0x%x\n", c);//0x123d0cf74.特定位取反用^
位异或:(任何数,其实就是1和0)与1位异或会取反,与0位异或无变化
(2)要取反的特定位为1,其他位取0,然后将这个数与原来的数进行位异或即可。
//异或:特定位取反用^//把寄存器值的bit4-bit7取反,其他位不变unsigned int a = 0x123d0cd7;unsigned int b = 0xf0;unsigned int c;c = a ^ b;printf("c=0x%x\n", c);//0x123d0c27三、用位运算构建特定二进制数
1.寄存器位操作经常需要特定位给特定值
(1)由上节课可以找到:对寄存器特定位进行置1或者清0或者取反,关键性的难点在于要事先构建一个特定的数,这个数和原来的值进行位与,位或,位异或等操作,既可达到我们对寄存器操作的要求。
(2)解法1:用工具,难度也不大,操作起来也不是太麻烦
解法2:自己写代码用位操作符号(主要是移位和位取反)来构建这个特定的二进制数
2.使用位移获取特定位为1的二进制数
(1)最简单的是用移位来获取一个特定位为1的二进制数。比如我们需要一个bit3-bit7为1(隐含意思是其他位全部为0)的二进制数,可以
1)先写出5位为1的数(0x1f==>bit0-bit4)
2)然后将这个数左移3位(0x1f<<3==》bit3-bit7)
(2)更难一点的:获取bit3-bit7为1,同时bit23-bit25为1,其他位为0
((0x1f<<3) | (0x7<<23))
#include<stdio.h>
int main() {//下面表达式的含义:位或说明这个数字由2部分组成,第一部分中左移2位说明第一部分从bit3开始//第一部分数字位0x1f说明这部分有5位,所以第一部分其实是bit3到bit7//第二部分的解读方法同样的,可知第二部其实是bit23到bit25unsigned int a;a = ((0x1f << 3) | (0x7 << 23));printf("a=0x%x\n", a);//a=0x38000f8return 0;
}3.再结合位取反获取特定位为0的二进制数
(1)现在我们要获取bit4-bit10为0,其余位全部为1的数。怎么做?
(2)利用上面讲的方法就可以:(0xf<<0) | (0x1fffff<<11)
unsigned int a;a = ((0xf << 0) | (0x1fffff << 11));printf("a=0x%x\n", a);//a=0xfffff80freturn 0;(3)但是这些存在问题:连续为1的位数太多了,这个数字本身就很难构造,所以这种方法的优势损失了
(4)思路是:先试图构造出这个数的位相反数,再取反得到这个数。(比如本例中要构造的数bit4-bit10为0,其他位为1),那我们先构造出一个bit4-bit10为1,其他位为0的数,然后对这个数按位取反即可。
//使用位移+取反unsigned int a;a = ~(0x7f<<4);printf("a=0x%x\n", a);//a=0xfffff80freturn 0;4.总结:
(1)如果你要的这个数比较少位为1,大部分位为0,则可以通过连续很多个1左移n位得到
(2)如果你想要的这个数是比较少位为0,大部分为1,则可以通过先根据其位反数,然后再位取反来得到
(3)如果你想要得到的数中连续1(连续0)的部分不止1个,那么可以通过多段分别构建,然后再彼此位与【|】即可。这个时候因为参与位或运算的各个数为1的位是不重复的,所以这时候的位或其实相当于几个数的叠加。
四、位运算实战
要置1用|,用清零用&,要取反用^,~和《《 》》用来构建特定二进制数。

1.例题1
给定一个整形数a,设置a的bit3,保证其他位不变。
a=a|(1<<3) 或者 a|=(1<<3)2.例题2
给定一个整形数a,设置a的bit3-bit7,保证其他位不变。
a=a|(0x1f<<3) 或者 a|=0x1f3.例题3
给定一个整形数a,清除a的bit15,保证其他位不变。
a=a& ~(0x1<<15) 或者 a&=~(0x1<<15) 4.例题4
给定一个整形数a,清除a的bit15-bit23,保证其他位不变。
a=a&(~(0x1ff<<15)) 或者 a&=(~(0x1ff<<15))5.例题5
给定一个整形数a,取出a的bit3-bit8
思路:
第一步:先讲这个数bit3-bit8不变,其他位全部清零--->a=a&(0x3f<<3)
第二步:再讲其右移3位得到结果
//第一步:把bit3到bit8的位保持不变,其余位全部清零
a=a& (0x3f<<3)
//第二步:将其右移3位
a>>=3;6.例题6
将一个寄存器的bit7-bit17中的值赋值937(其余位不受到影响)
关键点:不能影响其他位,并不知道原来bit7-bit17中装的值
思路
第一步:先将bit7-bit18全部清零,当然不能影响其他位
第二部:将bit7-bit17进行赋值【使用”|“因为我们要赋值】
//第一步:bit7-bit17全部清零
a&=~(0x7ff<<7);
//第二步:bit7-bit17赋值937
a|=(937<<7);7.例题7
将一个寄存器的bit7-bit17中的值+17(其余位不受到影响)
关键点:不知道原来的值是多少,
思路:
第一步:先读出原来的bit7-bit17的值
第二步:给这个值加17
第三步:将bit7-bit17清零
第四步:将第二步算出来的值写入bit7-bit17
unsigned int a=0xc30288f8;//第一步:先读出原来的bit7-bit17的值unsigned int tmp;tmp=a&(0x3ff<<7);//使用【&】和全1将这10位数进行计算tmp=tmp>>7//将其移动到低位取出//第二步:给这个值加17tmp+=17;//第三步:将bit7-bit17清零a=a & ~(0x3f<<7);//第四步:将第二步算出来的值写入bit7-bit17a=a| (tmp<<7);8.例题8
将一个寄存器的bit7-bit17中的值赋值937(其余位不受到影响),同时个bit21-bit25赋值17
方法1:
unsigned int a;
unsigned int tmp;
//第一步:先将bit7-bit17位全部置为0
a=a&~(0x7ff<<7);
//第二步:将这几位进行赋值
a=a|(937<<7);
//第三步:先取出bit21-bit25
tmp=a&(0x1f<<21);
tmp=tmp>>21;
//第四步:将17加上
tmp+=17;
//第五步:将bit21-bit25置为0
a=a&~(0x1f<<21);
//第六步;将tmp放回到bit21-bit25
a=a|(tmp<<21);方法2:
unsigned int a=0x30288f8;
a&=~((0x3ff<<7) | (0x1f<<21));//bit7-bit17和bit21-bit25全部清零
a|=((937<<7) | (17<<21));//937和17全部赋值五、用宏定义完成位运算
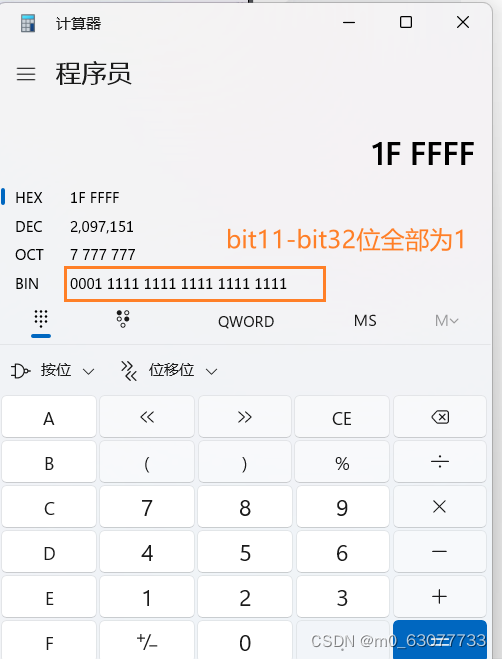
1.直接用宏来置位【赋1】,复位【赋0】(最右边为第1位)
1.1
用宏定义将32位数的第n位(右边其算,也就是bit0是第二位)置位【变成1】
//第一题:用宏定义将32位数的第n位(右边其算,也就是bit0是第二位)置位【变成1】
//1U:表示无符号1---》(x | (1U <<(n-1)))
#define SET_BIT_N(x,n) (x | (1<<(n-1)))//因为我们是从bit0开始算的
int main() {unsigned int a = 0;unsigned int b = 0;b=SET_BIT_N(a, 4);//对应bit3printf("0x%x", b);}1.2
第二题:用宏定义将32位数x的第n位(右边其算,也就是bit0是第1位)清零【变成0】
#include<stdio.h>//第二题:用宏定义将32位数x的第n位(右边其算,也就是bit0是第1位)清零【变成0】
#define CLEAR_BIT_N(x,n) (x&~(1U<<(n-1)))
int main() {//第二题unsigned int a = 0xffff;unsigned int b = 0;b= CLEAR_BIT_N(a, 4);//对应bit3printf("0x%x", b);//0xfff7}1.3
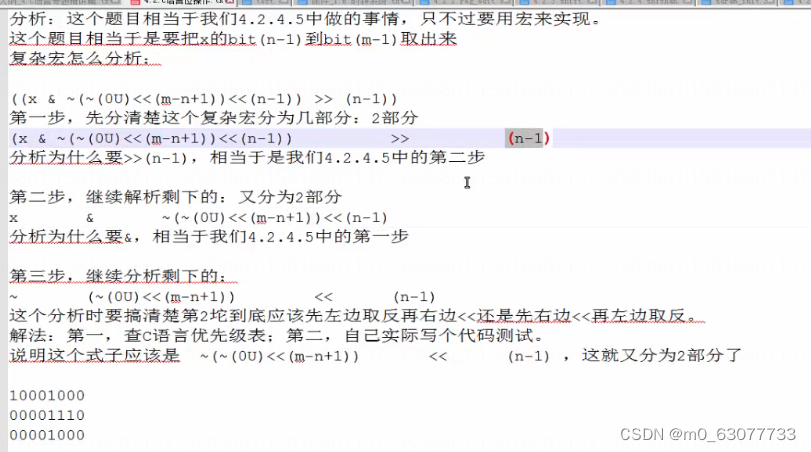
用宏定义将32位数x的第n位到第m位(右边起算,也就是bit0是第1位)置位【变成1】
我们需要一个算式得出(m-n+1)个1
算法:第一步:先得到32位1----》~(0U)
第二步:将第一步得到的数右移x位即可得到(m-n+1)个1-----》~(0U)>>(32-(m-n+1))
第三步:将得出的结果移回去原来的位置
//第三题:用宏定义将32位数x的第n位到第m位(右边起算,也就是bit0是第1位)置位【变成1】
//我们需要一个算式得出(m-n+1)个1
//算法:第一步:先得到32位1----》~(0U)
// 第二步:将第一步得到的数右移x位即可得到(m-n+1)个1-----》~(0U)>>(32-(m-n+1))
// 第三步:将得出的结果移回去原来的位置
#define CLEAR_BIT_N_M (x,n,m) (x| (((~0U)>>(32-(m-n+1)))<<(n-1)//第三题unsigned int a = 0x0;unsigned int b = 0;b = CLEAR_BIT_N_M(a,5,8);//对应bit3printf("0x%x", b);//2.截取遍历的部分连续位
#define GETBITS(x,n,m) ((x&~(~0U) << (m-n+1)) <<(n-1)) >> (n-1))
相关文章:

C位操作符
目录 一、位操作符 1.位与& 2.位或| 3.位取反~ 4.位异或^ 5.位与,位或,位异或的特点总结 6.左移位《《 右移位 》》 二、位与,位或,位异或在操作寄存器时的特殊作用 1.寄存器操作的要求(特定位改变而不…...

【linux进程(三)】进程有哪些状态?--Linux下常见的三种进程状态
💓博主CSDN主页:杭电码农-NEO💓 ⏩专栏分类:Linux从入门到精通⏪ 🚚代码仓库:NEO的学习日记🚚 🌹关注我🫵带你学更多操作系统知识 🔝🔝 Linux进程 1. 前言2. 操作系统…...
 - ‘0‘)
numString.charAt(i) - ‘0‘
numString.charAt(i) 表示获取字符串 numString 中第 i 个字符,这里假设该字符是数字 0 到 9 之间的一个字符。 0 是字符常量,表示数字 0 对应的字符。例如,字符 0 转换成数字就是 0,字符 1 转换成数字就是 1,以此类推…...

《Python 自动化办公应用大全》书籍推荐(包邮送书五本)
前言 随着科技的快速发展和智能化办公的需求增加,Python自动化办公成为了一种趋势。Python作为一种高级编程语言,具有简单易学、功能强大和开放源代码等优势,可以帮助我们更高效地完成日常办公任务。 Python自动化办公还可以帮助我们实现更…...

day57:ARMday4,程序状态寄存器读写指令、软中断指令、C和汇编的混合编程、开发板介绍
思维导图:有道云笔记...

el-cascader
场景: el-cascader lazy multiple 反显数据 非lazy的场景 selecetedOptions2: [[1, 2, 3],[1, 2, 4], ],可以正常回显;> ok lazy场景下: 是不可以回显的… 如果el-cascader是异步的单选 cascader默认会加载下个层级的(子…...

图论第3天----第841题、第463题
# 图论第3天----第841题、第463题 文章目录 一、第841题--钥匙和房间二、第463题--岛屿的周长 又继续开始修行,把图论这块补上,估计要个5-6天时间。 一、第841题–钥匙和房间 有向图的遍历。dfs遍历3部曲做,思路也较顺----访问过的&a…...

软件测试/测试开发丨利用ChatGPT 生成自动化测试脚本
点此获取更多相关资料 简介 自动化测试脚本可以模拟用户与应用程序的交互,例如点击按钮、输入数据、导航到不同的页面等等,以验证应用程序的正确性、性能和稳定性。 自动化测试在回归测试、冒烟测试等测试流程中都可以极大地起到节省时间、节省人力的作…...

3.3.OpenCV技能树--二值图像处理--图像形态学操作
文章目录 1.图像形态学运算简介2.图像开运算处理2.1.图像开运算处理简介2.2.图像开运算处理代码2.3.图像开运算处理效果 3.图像闭运算处理3.1.图像闭运算处理简介3.2.图像闭运算处理代码3.3.图像闭运算处理效果 4.图像形态学梯度处理4.1.图像形态学梯度处理简介4.2.图像形态学梯…...
这15个海运提单的雷区 你知道吗?
海运提单中英文对照 海运提单主要项目填制说明 1、托运人(Shipper):即与承运人签订运输契约,委托运输的货主,即发货人。在信用证支付方式下,一般以受益人为托运人;托收方式以托收的委托人为托运人。另外,根据《UCP500》…...
几道web题目
总结几道国庆写的web题目 [ACTF2020 新生赛]Include1 点进去发现就一个flag.php,源代码和抓包都没拿到好东西 结合题目猜是文件包含,构建payload ?filephp://filter/readconvert.base64-encode/resourceflag.php 得到base64编码过的flag,解码即可 此题…...

API接口大全分享,含短信API、IP查询API。。。
免费API接口大全分享,含短信API、IP查询API等。。。 语音验证码短信:拨打电话告知用户验证码,实现信息验证。短信验证码:可用于登录、注册、找回密码、支付认证等等应用场景。支持三大运营商,3秒可达,99.9…...

记录一次springboot使用定时任务中@Async没有生效的场景
环境说明 jdk21springboot 3.0.11 springcloud 2022.0.0 spring-cloud-alibaba 2022.0.0.0 在开发一个定时触发的任务的时候,由于开发执行任务的函数比较耗费时间,所以采用异步解决问题。 发现并没有按照预期的触发 经询问后,发现当前类的…...
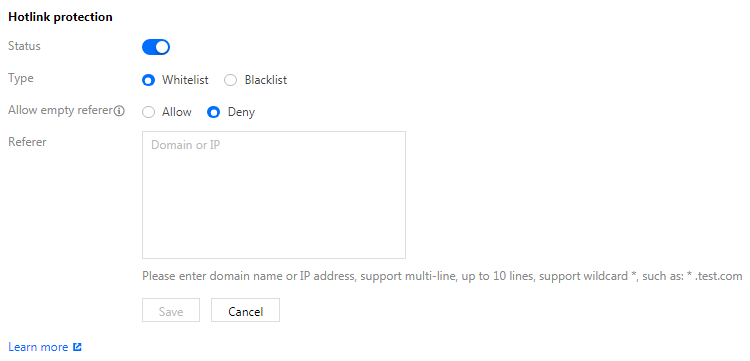
腾讯云/阿里云国际站免费账号:腾讯云国际站如何对象存储cos设置防盗链
简介 为了避免恶意程序使用资源 URL 盗刷公网流量或使用恶意手法盗用资源,腾讯云国际站给用户带来不必要的损失。腾讯云对象存储支持防盗链配置,建议您通过控制台的防盗链设置配置黑/白名单,来进行安全防护。 注意: 如果您访问对…...

python编程:使用 Pillow 将照片转换为1寸报名照片
引言: 在现代科技时代,我们经常需要调整和处理照片以适应特定的需求和用途。本文将介绍如何使用 wxPython 和 Pillow 库,通过一个简单的图形界面程序,将选择的照片转换为指定尺寸的 JPG 格式,并保存在桌面上。 C:\pyt…...
)
Aria2 for Mac (免HomeBrew)
Aria2 for Mac (免HomeBrew)-CSDN博客 之前搜索Aria2的安装方法,推荐的方法是使用HomeBrew安装。是,这个插件很省事,但启用条件是你安装了HomeBrew且运行起来需要再下十来个G的Xcode…… 这对急用的我非常不友好,当然,…...
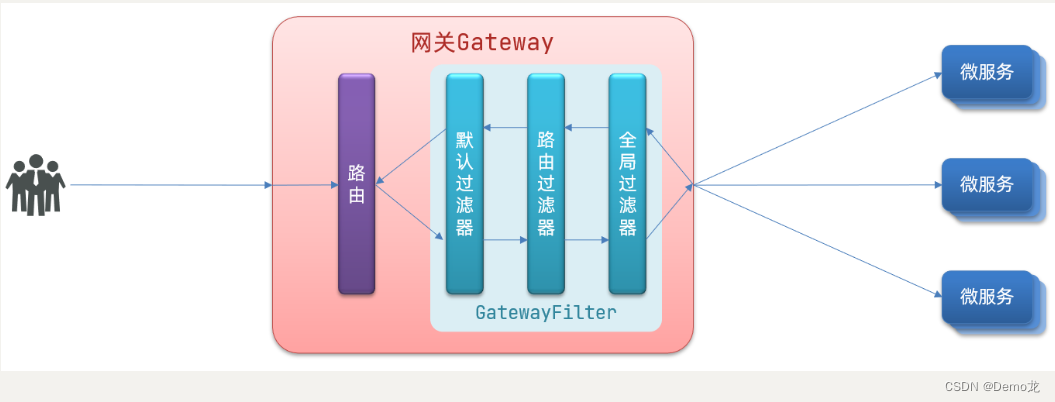
【Java】微服务——Gateway网关
目录 1.为什么需要网关2.gateway快速入门1)创建gateway服务,引入依赖2)编写启动类3)编写基础配置和路由规则4)重启测试5)网关路由的流程图 3.3.断言工厂3.4.过滤器工厂3.4.1.路由过滤器的种类3.4.2.请求头过…...

大厂笔试汇总
大厂笔试 华为笔试汇总1.交易系统的降级策略(二分法)2.获取最多食物(树形DP)3.小王的密码本(哈希)4.每日股票价格(单调栈)5.中庸行者(回溯)输入描述输出描述6.数字序列比大小(贪心)输入描述输出描述7、快递中转站8、互通设备集字节跳动中兴笔试华为笔试汇总 1.交易…...
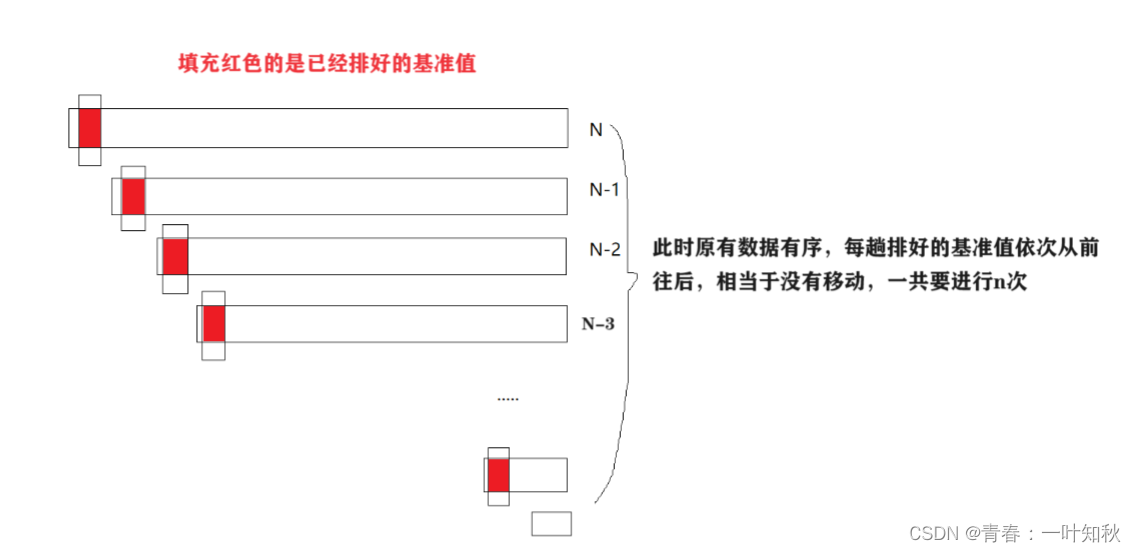
【数据结构】快排的详细讲解
目录: 介绍 一,递归快排确定基准值 二,递归遍历 三,非递归的快排 四,快排的效率 介绍 快排是排序算法中效率是比较高的,快排的基本思想是运用二分思想,与二叉树的前序遍历类似,…...
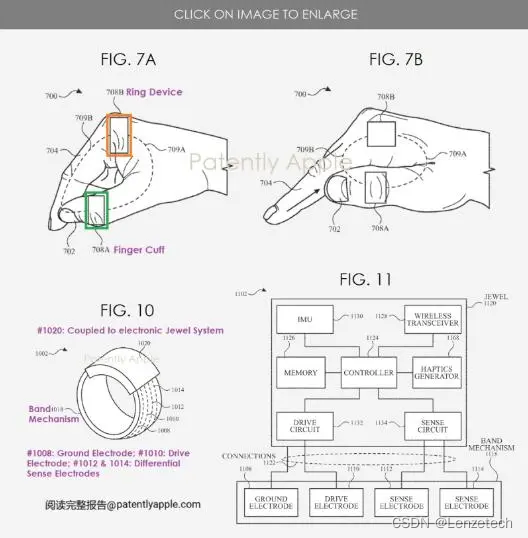
蓝牙资讯|三星推迟发布智能戒指Galaxy Ring,智能穿戴小型化是大趋势
根据外媒 The Elec 报道,Galaxy Ring这款戒指主要面向健康和 XR 头显市场,该智能戒指可能被延期至 2024 年第三季度后发布。 外媒声称三星 Galaxy Ring 的上市周期,主要取决医疗认证的相关审批时间,三星计划将在 2024 年第三季度…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

基于Java+MySQL实现(GUI)客户管理系统
客户资料管理系统的设计与实现 第一章 需求分析 1.1 需求总体介绍 本项目为了方便维护客户信息为了方便维护客户信息,对客户进行统一管理,可以把所有客户信息录入系统,进行维护和统计功能。可通过文件的方式保存相关录入数据,对…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...

抽象类和接口(全)
一、抽象类 1.概念:如果⼀个类中没有包含⾜够的信息来描绘⼀个具体的对象,这样的类就是抽象类。 像是没有实际⼯作的⽅法,我们可以把它设计成⼀个抽象⽅法,包含抽象⽅法的类我们称为抽象类。 2.语法 在Java中,⼀个类如果被 abs…...

Python竞赛环境搭建全攻略
Python环境搭建竞赛技术文章大纲 竞赛背景与意义 竞赛的目的与价值Python在竞赛中的应用场景环境搭建对竞赛效率的影响 竞赛环境需求分析 常见竞赛类型(算法、数据分析、机器学习等)不同竞赛对Python版本及库的要求硬件与操作系统的兼容性问题 Pyth…...